2. 江苏省水利科学研究院,江苏 南京 210017
物理模型和数学模型作为水利科学研究的常用工具,为工程设计、决策、施工及运行提供了有力支撑。虽然物理模型试验(常规比尺模型)和数值模型计算的水平日趋成熟,但也存在某些不足。对于大范围的流域、水系及江湖连通模拟,传统的常规比尺模型占地大、耗时费力、费用昂贵;由于水流泥沙及河床演变问题的复杂性,数学模型计算还存在计算条件概化不完善、参数调整主观性强、计算设备要求高等缺点,甚至对一些特殊物理现象还难以用数值方法进行描述和计算[1]。
自20世纪末,国外开始研究微尺度模型[2],从开发到投入应用历时20多年,成功运用于美国密西西比河、德国莱茵河等大小河流的河床演变及整治工程中[3]。具体做法是将研究区域按一定比尺制作在普通桌面上进行试验操作,放水试验全过程可在数分钟内完成。如Davies等[4]制作了平面比尺1:3 333,垂直比尺1:1 000的怀霍河(Waiho River,位于新西兰南部)微模型,模型尺度1.8 m×1.8 m,通过试验获得了怀霍河拦河坝对水流的横向限制作用影响了河床自然冲淤的结论,证明了微模型可用于工程对河流影响的定量预测。又如1996年,美国陆军工程师团等利用微模型技术探讨了密西西比河圣特菲丘克边渠丁坝等工程对流速和河床比降的影响,试验提出的方案帮助改善了附近鱼类及野生动物的生存环境[3, 5]。1997年,采用微模型技术研究了密西西比河24#船闸及大坝前水流流态的改善措施,解决了坝体及船员的安全问题[3, 5]等。国内对微模型的研究较少,毛野等[6]于2004年进行了长江和畅洲汊道采砂影响的动床微模型试验,其平面比尺为1:18 333,垂直比尺为1:500,变率为36.67,模型尺度为1.97 m×0.97 m×0.25 m,采用近景摄影解析技术研究了河床形态变化;郭少磊等[5]于2009年指出将传统实体模型与微尺度模型相结合,可解决黄河治理问题,应用前景十分广阔。李文全[7]于2012年强调微模型的尺度较小,制作及量测仪器是实现这项技术的关键。方红卫为数学模型计算提供边界条件,于2018年建立了黄河下游东霞院—汊3断面近800 km的三维变态微模型,模型范围35 m×15 m,坡降为1/250,横向比尺为1:1 400,垂向比尺为1:50,纵向比尺为1:28 000。
已有理论分析和实践表明,微尺度模型试验是一种模型比尺很小、几何变率很大的变态模型,它与传统的常规比尺模型本质相同,同样遵循相似理论、满足重力相似和阻力相似条件,以其模型规模小、试验周期短和经济性好等优势,可广泛应用于大尺度、大范围的河流、河口、海岸等水沙科学问题的研究。
鄱阳湖是我国第一大通江湖泊和第一大淡水湖。长江与鄱阳湖的水系连通、物质输运以及水沙交换、河床演变等江湖关系现状和演变,对防洪、生态环境和水资源综合利用等具有极其重要的意义。长江水倒灌入鄱阳湖是江湖关系的一个特殊过程,正确认识江湖倒灌现象及其影响,是研究长江与鄱阳湖关系的重要内容。实测资料显示,江湖倒灌影响因素多、作用范围广。近年来,随着自然演变、人类活动和全球气候环境变化的影响,江湖关系发生了很大变化[8]。已有研究大多采用资料分析、数学模型计算或常规比尺模型试验,耗费了大量人力物力。微模型试验法与资料分析法和数学模型计算法相比,具有物理概念清晰、直观形象的优点;与常规比尺模型相比,具有模型尺度小、试验周期短、经济性好等优势。由于微模型比尺较大、模型变率较大,其阻力相似问题和模型量测精度问题很难解决。微模型虽不能解决水流泥沙运动的所有问题,但能否用于研究长江与鄱阳湖包括“五河”尾闾的大范围江湖关系问题?如果可以,微模型遵循的相似律如何?采用的量测仪器等关键技术问题怎样解决?本文以长江与鄱阳湖的江湖倒灌影响为研究对象,通过分析、计算和实践,探讨了将微模型技术应用到江湖倒灌影响研究中的可能性和实际操作性,为微模型的推广应用提供依据。
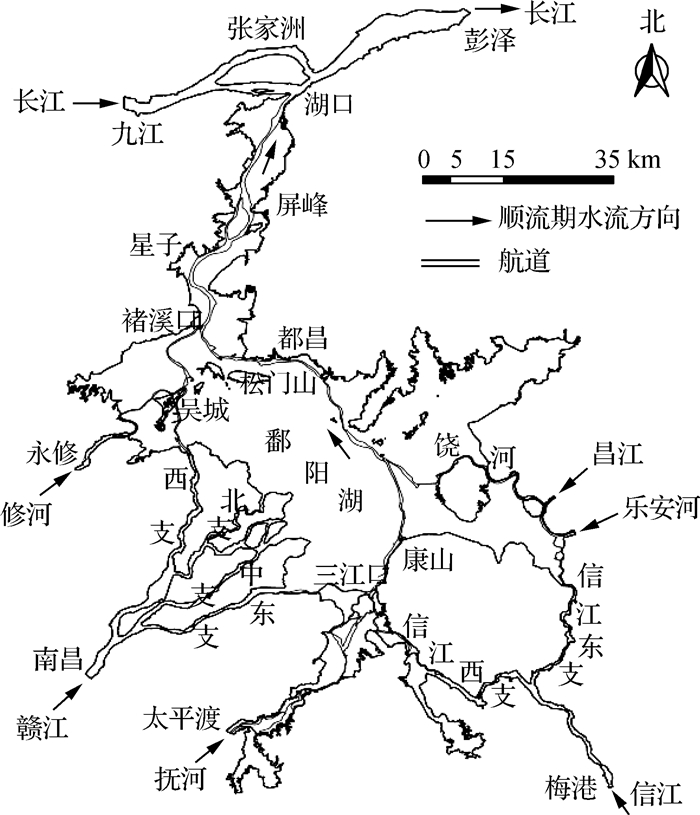
1 研究区域概况 1.1 流域概况鄱阳湖位于江西省北部,长江中下游南岸,是我国最大的淡水湖。湖泊水系呈辐射状(图 1),流域面积约16.22万km2,占长江流域面积的9.0%。鄱阳湖上接赣江、抚河、信江、饶河(由昌江和乐安河汇成)和修河(以下简称“五河”)及区间来水,调蓄后由湖口汇入长江,是一个过水性、吞吐性、季节性湖泊。湖区以松门山为界分南北两部分。南部宽广较浅,为主湖区,可分为东水道和西水道两部分;北部狭长较深,为入江水道区。全湖南北向最长173 km;东西平均宽16.9 km,最宽处74 km,入江水道最窄处的屏峰卡口约2.8 km,湖岸线长约1 200 km。湖盆自东向西、由南向北倾斜,南北最大高差约13 m。最低处屏风寺附近高程为-20.3 m,滩地高程在10 m左右。与江湖倒灌有关的长江段是九江至彭泽段(图 1),包括九江和张家洲,全长约73 km。
|
图 1 长江与鄱阳湖地理位置 Fig.1 Location of Yangtze River and Poyang Lake |
江湖作用全过程包括顺流期、顶托期和倒灌期三部分。年内大部分时间江湖作用都表现为顺流期,顺流时上游“五河”作用较强,湖水由“五河”汇入,于湖口流向长江。随着长江流域进入汛期,长江水流作用增强,顺流期发展成顶托期,后续可能出现两个过程,一是长江水流不能持续作用鄱阳湖,江湖顶托一段时间后跳过倒灌期,直接恢复顺流;二是长江水流对鄱阳湖的作用时间较长、作用强度较大,由江湖顶托发展成江水倒灌,倒灌一段时间后,随着长江水流的减弱,鄱阳湖恢复顺流。为方便研究,将未发生倒灌的过程称为无倒灌过程,不仅包括全年顺流期,还包括年内出现顶托的过程,此时湖口流量为正(图 1中水流方向);而发生倒灌的过程称为有倒灌过程,此时湖口流量为负。
2 研究资料与方法 2.1 基础资料水文资料为2006—2016年湖口日均流量、日均水位和实测流量,从《长江流域水文资料》中获得。模型研究范围广,地形年份难统一,采用1998年及2004—2011年实测地形拼接而成。其中,长江采用2006年和2010年1:10 000实测地形制作;鄱阳湖主湖区、赣江四支采用2010年1:10 000和2011年1:5 000实测地形制作,其他尾闾采用2005—2008年实测地形制作,入江水道航道内采用2004年12月1:5 000实测地形制作,湖区远离航道外用1998年4月1:10 000的地形补充。
2.2 有/无倒灌的典型年选取湖口位于江湖交汇处,在江湖相互作用时其水动力特征的变化最为敏感,可反映江湖倒灌的作用过程。由于地形资料主要年份是2006—2011年,现利用2006—2016年湖口日均流量数据统计得到湖口的倒灌情况(表 1),从2006—2016年《长江流域水文资料》的“资料说明”中了解鄱阳湖流域径流丰平枯年型划分情况,即丰水年有2010,2012,2015和2016年,平水年有2006和2014年,枯水年有2007,2008,2009,2011和2013年。
| 表 1 2006—2016年湖口站具体倒灌情况分析 Tab.1 Analysis of river water backward flowing into Poyang Lake at Hukou station from 2006 to 2016 |
由于2006—2016年的11年间,只有2006年、2010年和2015年全年未发生倒灌现象,因此选择2006(平水年)、2010(丰水年)和2015作为无倒灌的典型年。选择2008(枯水年)、2014(平水年)和2016(丰水年)作为有倒灌的典型年,原因是2008年湖口全年倒灌次数最多(共4次),是近十多年来倒灌情况最为复杂的一年,对应枯水年;2016年日均倒灌流量最大,2016年7月3日的日均倒灌流量高达8 470 m3/s,倒灌强度最高,代表强倒灌情况,对应丰水年;而平水年发生倒灌的只有2014年,其倒灌次数最少(1次),代表弱倒灌情况。
3 定床微模型试验方法 3.1 相似理论与相似条件微模型不同于国外沙盘式的微尺度模型,也不同于国内常规比尺的大型物理模型,而是介于两者之间的规模较小仍放在试验厅进行试验的微模型。根据水流运动方程和模型相似理论[9-11],微模型必须满足几何相似、重力相似和阻力相似。
| $ 重力相似:\;\;\;\;\;\;\;\;\;\;{\lambda _v} = \lambda _{_H}^{^{1/2}} $ | (1) |
| $ 阻力相似:\;\;\;\;\;\;\;\;\;\;{\lambda _n} = \lambda _{_H}^{^{2/3}}\lambda _{_L}^{^{1/2}} $ | (2) |
| $ 流量比尺:\;\;\;\;\;\;\;\;\;\;{\lambda _Q} = {\lambda _v}{\lambda _L}{\lambda _H} $ | (3) |
式中:λL为平面比尺;λH为垂直比尺;λv为流速比尺;λn为糙率比尺;λQ为流量比尺。
3.2 平面比尺选择江湖倒灌研究区域包括长江、鄱阳湖和“五河”尾闾,天然范围约95 km×164 km(图 1)。其中,长江段上起九江下至彭泽,长约73 km,流域面积300 km2;鄱阳湖包括整个湖盆区域,南北向最长173 km,东西平均宽16.9 km,湖域面积约2 800 km2;尾闾段包括赣江四支、抚河、信江东西支、乐安河、昌江、修河等。赣江从南昌至湖区(长约58 km)、抚河从太平渡至三江口(长约43 km)、信江从梅港至三江口(长约75 km)、修河从永修至湖区(长约14 km)。根据试验厅场地条件,选定模型平面比尺λL=6 500,实际占地约15 m×25 m。模型各河段堤线间断面宽度特征见表 2。
| 表 2 微模型各河段堤线间断面宽度特征(λL=6 500) Tab.2 Characteristics of section width of microscale physical model (λL=6 500) |
根据《内河航道与港口水流泥沙模拟技术规程》[10]和《河工模型试验规程》[11]的规定,模型需同时满足雷诺数大于1 000和水深大于1.5 cm的限制条件。依据这两个条件,可以确定微模型垂直比尺范围。计算用到的湖口平均流速、平均水深从相应年份《长江流域水文资料》的“实测流量成果表”中获得。
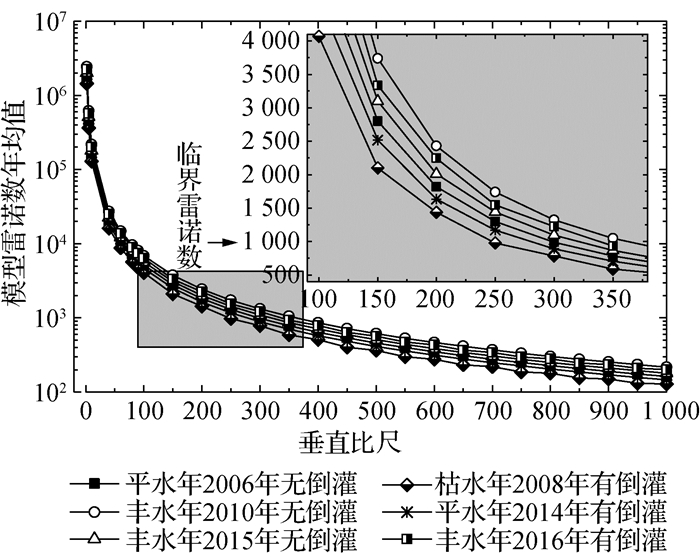
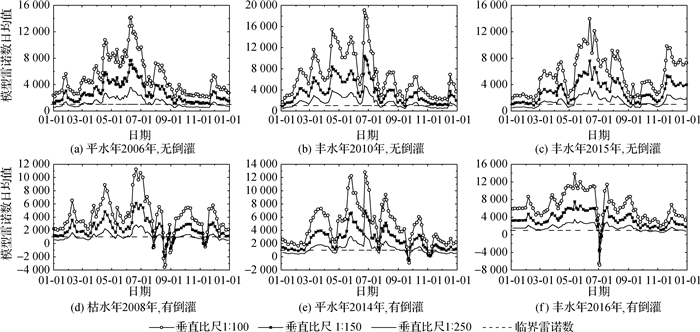
3.3.1 垂直比尺对模型雷诺数影响图 2给出了湖口站日雷诺数年均值与垂直比尺(λH=2,5,10,40,60,80,90,100~1 000(间距为50取值)共26种情况)的关系。图 3给出了湖口站垂直比尺为1:100,1:150及1:250时模型日雷诺数的变化过程。由两图可知:①不同年份的模型雷诺数年内变化趋势相同(图 3),都表现为鄱阳湖主汛期(4—6月)时较大、非汛期时较小;②鄱阳湖径流的丰、枯以及有无倒灌或倒灌强度大小(图 3(d)年内倒灌4次、图 3(e)弱倒灌、图 3(f)强倒灌)对模型雷诺数的影响,总体趋势是随着模型垂直比尺的增大,模型雷诺数变化减缓(图 2);③当垂直比尺λH=250时,不同年份湖口站模型日雷诺数年均值都大于1 000(图 2),但由于湖口站日均雷诺数年内变化较大,全年仍有部分时间(尤其是鄱阳湖非汛期)日雷诺数小于1 000(图 3);④垂直比尺λH=150时,除发生倒灌的初期和倒灌即将结束的个别天外(图 3),湖口全年日雷诺数均大于1 000。
|
图 2 湖口站模型日雷诺数年均值与垂直比尺关系 Fig.2 Relationships between annual average Reynolds number of microscale model and vertical scales at Hukou station |
|
图 3 湖口站模型日雷诺数过程线 Fig.3 Daily average Reynolds number process lines at Hukou station given by microscale model |
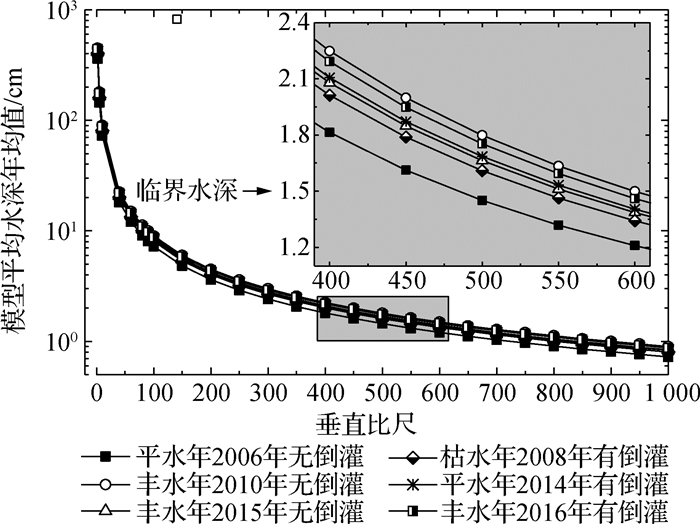
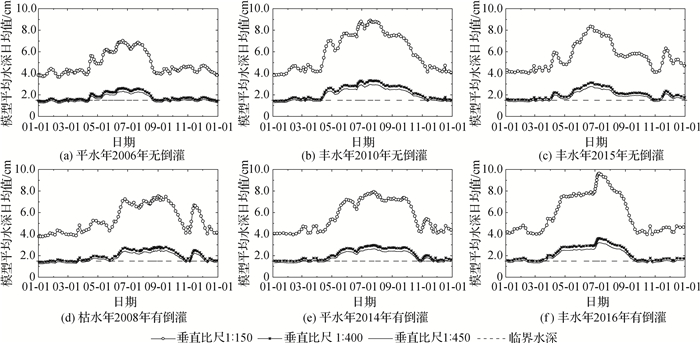
图 4给出了湖口站模型日均水深的年均值与垂直比尺(λH=2,5,10,40,60,80,90,100~1 000(间距为50)共26种情况)的关系。图 5给出了垂直比尺为1:150,1:400及1:450时湖口站模型日平均水深变化过程。由图 4和5可知:①不同年份模型平均水深表现为鄱阳湖主汛期(4—6月)时较大、非汛期时较小(图 5);②有无倒灌对湖口站同期模型平均水深影响不大(如图 5(a)与5(e)),而鄱阳湖径流的丰、枯对模型平均水深的影响整体趋势是Hm丰>Hm平>Hm枯(图 5(d),5(e)和5(f));③垂直比尺λH=450时,湖口站模型日平均水深的年均值都大于1.5 cm(图 4),但湖口站模型日均水深年内变化也较大,全年有部分时间(尤其是鄱阳湖非汛期)模型水深小于1.5 cm(图 5);④垂直比尺λH=400时,湖口全年模型日平均水深均大于1.5 cm。
|
图 4 湖口站模型日平均水深年均值与垂直比尺关系 Fig.4 Relationships between annual average of daily mean water depth and vertical scales at Hukou station given by microscale model |
|
图 5 湖口站模型日平均水深过程线 Fig.5 Process of daily average water depth at Hukou station by microscale model |
垂直比尺满足雷诺数限制要求为λH≤150,满足水深限制要求为λH≤400,同时满足这两个限制要求的是λH≤150。考虑到①临界雷诺数是在顺直水槽内得出的,由于河道形态不规整或局部地形影响,水流达到阻力平方区的临界雷诺数会有所减小;②微模型采用流量变态法来解决阻力相似问题时,模型实际放水流量为原来的1.5倍,更有利于水流进入阻力平方区(后文详述);③微模型垂直比尺λH=150时,无论是否发生倒灌,也无论鄱阳湖径流的丰枯,湖口站的模型雷诺数Rem=(1 059~10 376)>1 000(发生倒灌的那几天除外,倒灌时模型雷诺数为负)、模型平均水深Hm=3.6~9.6 cm,大于1.5 cm;统计得到典型年鄱阳湖湖区都昌处滩地年均水位12.35 m、康山附近年均水位14.05 m,湖区滩地高程在10.00 m左右。在垂直比尺λH=150时,计算得湖区滩地模型平均水深H湖区m=1.6~2.7 cm,大于1.5 cm。所以最终选择微模型的垂直比尺为λH=150。
3.4 阻力相似问题 3.4.1 微模型阻力相似难题河段原型糙率nP为0.017~0.024[12],当微模型平面比尺λL=6 500,垂直比尺λH=150时,由式(1)得λv=
当模型水流阻力达不到设计要求时,模型水面线会发生偏离。为了达到水面线的相似,可适当增加或减少试验流量,以达到模型水面线相似,即流量变态法[7],其实质是改变了模型的流速比尺。
对于宽浅河流(R≈H),由谢才公式可得如下比尺关系:
| $ {\lambda _v} = \lambda _{_n}^{1}{\lambda _H}^{7/6}\lambda _{_L}^{^{1/2}} $ | (4) |
模型中的流速和弗劳德数分别为vm和Frm,采用流量变态后模型中的流速、流量、糙率、弗劳德数分别变为v′m,Q′m,n′m和Fr′m。定义模型中流量变态后的物理量与按重力相似要求的相应物理量之比,即物理量的变率为:
| $ {\eta _n} = n{\prime _{\rm{m}}}n_{\rm{m}}^{^{ - 1}}\;, {\eta _v} = v{\mathit{'}_{\rm{m}}}\mathit{v}_{\rm{m}}^{ - 1}\;, {\eta _Q} = Q{\mathit{'}_{\rm{m}}}Q_{\rm{m}}^{ - 1}\;, {\eta _{Fr}} = Fr{\mathit{'}_{\rm{m}}}Fr_{\rm{m}}^{ - 1} $ | (5) |
根据式(4)和(5),可导出各物理量变率的关系:
| $ {\lambda _v}\lambda {\prime _v}^{1} = (\lambda _{_n}^{^{1}}{\lambda _H}^{7/6}\lambda _{_L}^{1/2})(\lambda {\prime _n}\lambda _{_H}^{^{7/6}}\lambda _{_L}^{^{1/2}}) = \lambda _{_n}^{^{1}}\lambda {\prime _n} $ | (6) |
| $ \begin{array}{l} {\eta _n}{\eta _v} = \left( {n{\mathit{'}_{\rm{m}}}n_{\rm{m}}^{ - 1}} \right)\left( {v{\mathit{'}_{\rm{m}}}v_{\rm{m}}^{ - 1}} \right) = \left( {n{\mathit{'}_{\rm{m}}}n_{\rm{m}}^{ - 1}} \right)\left( {{\lambda _\mathit{v}}\lambda \mathit{'}_v^{ - 1}} \right) = \left( {n{\mathit{'}_{\rm{m}}}n_{\rm{m}}^{ - 1}} \right)\left( {\lambda _n^{ - 1}\lambda {\mathit{'}_n}} \right) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {n{\mathit{'}_{\rm{m}}}n_{\rm{m}}^{ - 1}} \right)\left( {\left( {n_{\rm{P}}^{ - 1}{n_{\rm{m}}}} \right)\left( {{n_{\rm{P}}}n\mathit{'}_{\rm{m}}^{ - 1}} \right)} \right) = 1 \end{array} $ | (7) |
| $ \begin{array}{l} {\eta _n}{\eta _Q} = \left( {n{\mathit{'}_{\rm{m}}}n_{\rm{m}}^{ - 1}} \right)\left( {\mathit{Q}{\mathit{'}_{\rm{m}}}Q_{\rm{m}}^{ - 1}} \right) = \left( {n{\mathit{'}_{\rm{m}}}n_{\rm{m}}^{ - 1}} \right)\left( {{\lambda _\mathit{Q}}\lambda \mathit{'}_Q^{ - 1}} \right) = \left( {n{\mathit{'}_{\rm{m}}}n_{\rm{m}}^{ - 1}} \right)\left( {\left( {{\lambda _v}{\lambda _L}{\lambda _H}} \right)\left( {\lambda \mathit{'}_v^{ - 1}\lambda _L^{ - 1}\lambda _H^{ - 1}} \right)} \right) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {n{\mathit{'}_{\rm{m}}}n_{\rm{m}}^{ - 1}} \right)\left( {{\lambda _v}\lambda \mathit{'}_v^{ - 1}} \right) = 1 \end{array} $ | (8) |
| $ \begin{array}{l} {\eta _n}{\eta _{Fr}} = \left( {n{\mathit{'}_{\rm{m}}}n_{\rm{m}}^{ - 1}} \right)\left( {\mathit{Fr}{\mathit{'}_{\rm{m}}}\mathit{Fr}_{\rm{m}}^{ - 1}} \right) = \left( {n{\mathit{'}_{\rm{m}}}n_{\rm{m}}^{ - 1}} \right)\left( {{\mathit{{\lambda }}_{\mathit{Fr}}}\mathit{{\lambda }}\mathit{'}_{\mathit{Fr}}^{ - 1}} \right) = \left( {n{\mathit{'}_{\rm{m}}}n_{\rm{m}}^{ - 1}} \right)\left( {\left( {{\mathit{{\lambda }}_v}\mathit{{\lambda }}_H^{ - 1/2}} \right)\left( {\mathit{{\lambda }}\mathit{'}_v^{ - 1}\mathit{{\lambda }}_H^{1/2}} \right)} \right) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {n{\mathit{'}_{\rm{m}}}n_{\rm{m}}^{ - 1}} \right)\left( {{\mathit{{\lambda }}_v}\mathit{{\lambda }}\mathit{'}_v^{ - 1}} \right) = 1 \end{array} $ | (9) |
| $ n{\mathit{'}_{\rm{m}}}n_{\rm{m}}^{ - 1} = {v_{\rm{m}}}v\mathit{'}_{\rm{m}}^{ - 1} = {Q_{\rm{m}}}Q\mathit{'}_{\rm{m}}^{ - 1} = F{r_{\rm{m}}}Fr\mathit{'}_{\rm{m}}^{ - 1} $ | (10) |
式中:ηn为糙率变率;ηv为流速变率;ηQ为流量变率;ηFr为弗劳德数变率。
由式(7)~(9)可知,只有各比值乘积等于1时,才能保证阻力相似,这要求模型糙率较大而难以实现。由式(10)可知,若模型中增加试验流量,即Q′m>Qm,则有v′m>vm,Fr′m>Frm和n′m<nm(降低了模型对糙率的要求)。即在允许重力相似发生适当偏离时,可达到阻力相似的要求。
3.4.3 流量变率选择及比尺汇总由原型糙率和几何比尺计算得微模型糙率nm=0.049~0.069,而实际上通过常用加糙手段,微模型的实际糙率n′m只能为0.015~0.045。由式(5)得糙率变率ηn=0.31~0.66,由式(8)得流量变率ηQ=1.52~3.24。根据微模型的率定和验证试验,最终确定流量变率为1.5(后文详述)。模型比尺汇总见表 3。
| 表 3 模型比尺汇总 Tab.3 Summary of micro model scale |
流量变态法变态1.5倍后,模型雷诺数变为原来的1.5倍。在探讨垂直比尺对模型雷诺数影响(图 2和3)时,利用的是未经流量变态处理的结果。可见,流量变态法更有利于微模型的水流进入阻力平方区,更有利于实现水流流态和阻力的相似。
流量变态法使得模型重力相似发生了偏离。在Q′m=1.5Qm时,重力相似偏离程度为ΔFr=1-λ′v/λ′H=1-8.16/1501/2=33%。目前常规比尺模型对重力相似允许的偏离程度尚无统一结论,李昌华[9]认为平原河流允许重力相似有50%的偏差;水利部试验规程[11]中指出“重力相似允许的偏离程度应小于25%”;交通部试验规程[10]中指出“在模型设计时,允许重力相似偏离值不宜超过30%”。本模型重力相似偏离33%,接近相关规程规定的允许范围,故在保证阻力相似前提下,允许部分重力相似偏离,可以用来研究江湖倒灌的洪水传播和水面线问题。
3.5 微模型试验中的测控仪器方案进出口控制:采用平水塔及三角形量水堰控制九江进口流量、用玻璃转子流量计控制“五河”尾闾和湖区区间的进口流量、用翻板式尾门通过计算机及跟踪式水位仪自动控制彭泽的出口水位。
水位测量:微模型水位最小变幅为±0.01 mm,现有水位测针或跟踪式水位仪(分辨率为0.1 mm)不满足水位精度要求,用边坡上垂直高度较小变化引起斜边较大变化的原理来解决。将测点处水位用连通器引入到带有刻度线的斜坡(边坡系数为m)上。先利用照相机对斜坡水位变化过程L(t)进行实时摄影,再进行后期处理,进而获得测点处水位变化过程Z(t)。
流速测量:悬桨流速传感器可测量流速大于1 cm/s的流速。长江与鄱阳湖微模型范围内,模型流速大于3cm/s,采用常规流速测量系统和粒子跟踪测速技术(PTV)配合测量流速。
3.6 微模型江湖倒灌率定与验证由前文所述,流量变态倍数为1.52~3.24。采用2012年9月22—24日无倒灌实测资料对微模型水位、断面流速分布和流量进行率定,模型中在张家洲尾—彭泽和张家洲左汊局部采用直径为1~2 cm,间距10 cm的梅花型加糙方法加糙。经反复试验,确定流量变态倍数为1.5(即流量变率ηQ=1.5);利用2016年7月2—7日的倒灌过程对流量变态倍数取值及倒灌时间、倒灌流量进行验证,验证结果见表 4~5及图 6。
| 表 4 微模型水位验证结果(2012-09-22) Tab.4 Water level validation results of microscale model (22 Sep. 2012) |
| 表 5 微模型典型断面流量验证结果(2012年) Tab.5 Discharge verification results of typical cross-sections of microscale physical model (2012) |
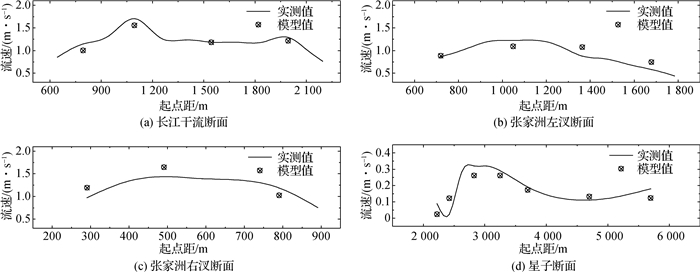
|
图 6 微模型典型断面流速分布验证结果(2012-09-22) Fig.6 Velocities distribution verification results of typical cross-sections of microscale model (22 Sep. 2012) |
由表 4可见,微模型中长江水位略低于天然,入江水道和鄱阳湖湖区水位略高,总体上基本接近天然,其误差在±0.08 m以内;断面流量,除长江张家洲左汊断面流量相对误差为-10.1%以外,其他断面的流量误差都在±4.85%以内(表 5),分析张家洲左汊流量偏小的原因是地形与水文条件不完全匹配,导致断面流速分布与天然状态存在一定差异(图 6)。倒灌时间和倒灌流量:2016年天然倒灌时间为7月2—7日,倒灌历时6 d,最大倒灌流量为7月3日的8 470 m3/s,微模型模拟结果为倒灌时间7月2—8日,倒灌历时7 d,最大倒灌流量为7 600 m3/s,相对误差为-10.3%。分析产生误差的主要原因,仍然是由于地形资料与水文条件不匹配所致。总的来说,所建微模型能成功复演长江、鄱阳湖与“五河”尾闾水流运动特性,可用于研究大范围江湖倒灌现象及江湖关系相关问题。
4 结语(1) 微模型与常规比尺模型一样,遵循的模型相似律为必须满足阻力相似。
(2) 长江对鄱阳湖倒灌影响的微模型,选择平面比尺λL=6 500,垂直比尺λH=1:150,可满足雷诺数和模型水深限制要求;经试验验证,在流量变态1.5倍时,采用常用模型加糙方法,可满足微模型阻力相似,其重力相似偏离33%。
(3) 在传统模型量测仪器的基础上适当改进,可实现微模型水位、流速等物理量的量测。
(4) 微模型试验虽不能解决水流泥沙运动的所有问题,但微模型以其占地小、试验周期短、经济性好等明显优势,对研究河流、湖泊、河口、海岸等大尺度和复杂水沙运动问题,具有广阔的应用和发展前景。
| [1] |
MARTIN J L, MCCUTCHEON S C. Hydrodynamics and transport for water quality modeling[M]. Boca Raton: CRC Press, 2018.
|
| [2] |
DAVINROY R D. Physical sediment modeling of the Mississippi River on a micro scale[D]. Missouri: University of Missouri-rolla, 1994.
|
| [3] |
王志寰, 范红霞, 朱立俊, 等. 长江洪水对鄱阳湖倒灌影响及微模型研究进展综述[J]. 泥沙研究, 2019, 44(1): 59-66. ( WANG Zhihuan, FAN Hongxia, ZHU Lijun, et al. Review on the influence to the Poyang Lake by flowing backward of the Yangtze River and the study processes of micro physical model[J]. Journal of Sediment Research, 2019, 44(1): 59-66. (in Chinese)) |
| [4] |
DAVIES T R H, MCSAVENEY M J, CLARKSON P J. Anthropic aggradation of the Waiho River, Westland, New Zealand: microscale modelling[J]. Earth Surface Processes and Landforms, 2003, 28(2): 209-218. DOI:10.1002/esp.449 |
| [5] |
郭少磊, 江恩惠, 李军华. 微尺度模型在密西西比河治理中的应用[J]. 人民黄河, 2009, 31(3): 32-33. ( GUO Shaolei, JIANG Enhui, LI Junhua. Application of microscale model in Mississippi River regulation[J]. Yellow River, 2009, 31(3): 32-33. DOI:10.3969/j.issn.1000-1379.2009.03.015 (in Chinese)) |
| [6] |
毛野, 黄才安, 陈建华, 等. 长江镇江段河道采砂的影响及其控制利用的试验研究[J]. 泥沙研究, 2004(3): 41-45. ( MAO Ye, HUANG Caian, CHEN Jianhua, et al. Experimental study on the effects of sand mining on the riverbed deformation in Zhenjiang reach and its application[J]. Journal of Sediment Research, 2004(3): 41-45. DOI:10.3321/j.issn:0468-155X.2004.03.006 (in Chinese)) |
| [7] |
李文全. 微型河工模型试验技术与理论基础初探[J]. 水运工程, 2012(10): 69-73. ( LI Wenquan. Preliminary study on basic principle of micro scale physical selection modeling (MICRO MODELING)[J]. Port and Waterway Engineering, 2012(10): 69-73. DOI:10.3969/j.issn.1002-4972.2012.10.013 (in Chinese)) |
| [8] |
HUANG F, WU Y, QIAN B, et al. An environmental flow assessment of a river's blocking effect on a lake in a river-lake system: application in the Yangtze-Poyang system[J]. Environmental Monitoring and Assessment, 2018, 190(8): 1-12. |
| [9] |
李昌华, 金德春. 河工模型试验[M]. 北京: 人民交通出版社, 1981. ( LI Changhua, JIN Dechun. River model test[M]. Beijing: China Communications Press, 1981. (in Chinese))
|
| [10] |
JTS/T 231-4-2018内河航道与港口水流泥沙模拟技术规程[S]. (JTS/T 231-4-2018 Technical regulation of modeling for flow and sediment in inland waterway and harbour[S]. (in Chinese))
|
| [11] |
SL 99—2012河工模型试验规程[S]. (SL 99—2012 Regulation for river model test[S]. (in Chinese))
|
| [12] |
王志寰.长江对鄱阳湖洪水顶托与倒灌水动力数学模型研究[D].南京: 南京水利科学研究院, 2014. (WANG Zhihuan. Study on hydrodynamic mathematical model for backwater effect of flood and backflowing from Yangtze River into Poyang Lake[D]. Nanjing: Nanjing Hydraulic Research Institute, 2014. (in Chinese))
|
2. Jiangsu Hydraulic Research Institute, Nanjing 210017, China
 2019
2019 