2. 同济大学 土木工程学院,上海 200092;
3. 上海千年城市规划工程设计股份有限公司,上海 201108
在水利、建筑及港口工程等领域,随着荷载量级的不断增大,组合工字形或箱形薄壁截面深梁得到越来越广泛的应用。深梁在横力弯曲时,由于剪应力沿横截面高度的分布不均匀,剪应变也沿截面高度同步变化,从而导致横截面不能保持平面而翘曲。当梁在各相邻横截面上的剪力都相等时,则各截面的翘曲程度也相同[1],相邻横截面间纵向纤维伸长相同,即为同步翘曲影响。但在分布荷载作用下,梁在各横截面上的剪力不同,各横截面的翘曲程度也不同,相邻横截面纵向纤维的伸长也就不相同[2],此时既要考虑同步翘曲影响,也要考虑不同步翘曲影响。同时翼缘受力使得层间纤维相互挤压[3]也是影响因素之一。
长期以来,众多学者致力于深梁理论及应力计算的研究,针对矩形截面深梁的应力计算已有很多研究成果[2, 4-7],但工字形截面梁因其截面复杂,与矩形梁相比受力机理更为复杂,精确解析解难以求出[8]。王正中等 [9-11]探索了工字形截面深梁的应力计算方法,研究了梁内弯应力的分布规律。利用材料力学方法考虑了不同步翘曲影响,给出了工字形截面应力计算式;通过假定工字形梁翼缘、腹板传力方式,采用弹性力学半逆解法推导出了不同支座形式应力计算式;给出了层间挤压应力的计算方法,并指出其应力值随梁跨度和高度方向变化,不可忽略。但所采用弹性力学和有限元方法分别对工字形矩形截面梁进行应力分析,所得公式解法复杂,物理含义不够明晰,不易推广至其他特殊形状截面梁的计算。
本文首先根据闸门面板与主梁翼缘连接形式,忽略其扭转变形,同时摒弃材料力学中平截面及纵向纤维互不挤压的假定,利用叠加思想,建立横力弯曲下工字形截面深梁力学模型,推导出考虑同步翘曲、不同步翘曲和挤压影响的应力解析计算式,揭示了薄壁深梁弯曲、剪切与挤压的耦合变形机理。进而将本文解以及文献[9-10]解与有限元数值计算结果进行比较,分析其分布规律和适用范围。
1 工字形截面梁的截面特征根据图 1定义工字形截面几何特征参数,各参数计算如下。

|
图 1 工字形截面尺寸 Fig.1 Dimensions of I-beam cross section |
设:
| $ \frac{{{A_1}}}{{{A_f}}} = {\beta _1}, \frac{{{A_2}}}{{{A_f}}} = {\beta _2}, \frac{{{h_1}}}{h} = {\alpha _1}, \frac{{{h_2}}}{h} = {\alpha _2}, \theta = \frac{{{b_2}}}{{{b_1}}} $ | (1) |
则:
| $ {\alpha _1} = \frac{{1 + 2{\beta _2}}}{{2\left( {1 + {\beta _1} + {\beta _2}} \right)}}, {\alpha _2} = \frac{{1 + 2{\beta _1}}}{{2\left( {1 + {\beta _1} + {\beta _2}} \right)}} $ | (2) |
| $ I = \frac{{{A_f}{h^2}}}{{12}}\left( {1 + 12{\beta _1}\alpha _1^2 + 12{\beta _2}\alpha _2^2} \right) $ | (3) |
| $ {S^ * } = \left\{ {\begin{array}{*{20}{c}} {\frac{{{b_1}}}{2}\left( {\alpha _1^2{h^2} - y_1^2} \right)}&{b\left( {{y_1}} \right)}&{ = {b_1}}&{\left( {{\alpha _1}{h_0} \le {y_1} \le {\alpha _1}h} \right)}\\ {{A_1}{\alpha _1}{h_0} + \frac{\delta }{2}\left( {\alpha _1^2h_0^2 - y_1^2} \right)}&{b\left( {{y_1}} \right)}&{ = \delta }&{\left( {0 \le {y_1} \le {\alpha _1}{h_0}} \right)}\\ { - {A_2}{\alpha _2}{h_0} + \frac{\delta }{2}\left( {\alpha _2^2h_0^2 - y_1^2} \right)}&{b\left( {{y_1}} \right)}&{ = \delta }&{\left( { - {\alpha _2}{h_0} \le {y_1} \le 0} \right)}\\ { - \frac{{{b_2}}}{2}\left( {\alpha _2^2{h^2} - y_1^2} \right)}&{b\left( {{y_1}} \right)}&{ = {b_2}}&{\left( { - {\alpha _2}h \le {y_1} \le - {\alpha _2}{h_0}} \right)} \end{array}} \right. $ | (4) |
| $ \int_{\min } {\frac{{{S^ * }{\rm{d}}{y_1}}}{{b\left( {{y_1}} \right)}}} = \left\{ \begin{array}{l} \frac{{{A_1}\alpha _1^2h_0^2}}{\delta } + \frac{{\alpha _1^2{h^2}y}}{2} - \frac{{{y^3}}}{6}\;\;\;\;\left( {{\alpha _1}{h_0} \le y \le {\alpha _1}h} \right)\\ \frac{{{A_1}{\alpha _1}{h_0}}}{\delta }y + \frac{{\alpha _1^2h_0^2y}}{2} - \frac{{{y^3}}}{6}\;\;\;\;\left( {{\alpha _1}{h_0} \le y \le 0} \right)\\ \frac{{{A_2}{\alpha _2}{h_0}}}{\delta }y + \frac{{\alpha _2^2h_0^2y}}{2} - \frac{{{y^3}}}{6}\;\;\;\;\left( { - {\alpha _2}{h_0} \le y \le 0} \right)\\ \frac{{{A_1}\alpha _1^2h_0^2}}{\delta } + \frac{{\alpha _1^2{h^2}y}}{2} - \frac{{{y^3}}}{6}\;\;\;\;\left( { - {\alpha _2}h \le y \le - {\alpha _2}{h_0}} \right) \end{array} \right. $ | (5) |
式中:A1,A2分别为上下翼缘的面积;h1,h2分别为上下翼缘距中性轴的距离;h为梁高;b(y1)为距中性轴y1处横截面宽度,即1,面积为A;I为工字形截面对中性轴的惯性矩;S*为横截面距中性轴y1以外部分面积对中性轴的面积矩。
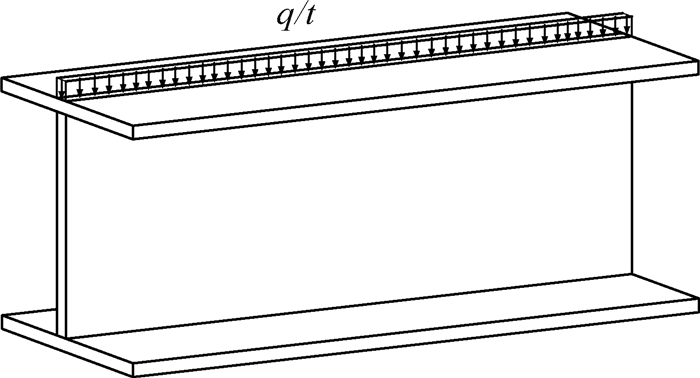
2 单轴对称工字形截面正应力计算式推导工字形截面单跨简支深梁是工程中常见的构件形式,而由于闸门主梁与面板直接相连,主梁上翼缘分载作用相对面板而言较小,故该处假定由腹板处承担上翼缘载荷,计算简图如图 2所示。图 2中的q=dQ/dz,为梁上的分布荷载,以向下为正,Q为剪力。
|
图 2 计算模型 Fig.2 Computation model |
文献[9]利用材料力学法建立工字形截面梁。当各截面剪力不同时,正应力计算模型即考虑不同步翘曲对正应力的影响,其计算式为:
| $ {\sigma _x} = \frac{{My}}{I} + \frac{{2(1 + \mu )q}}{I}\int_0^y {\frac{{{S^*}}}{{b\left( {{y_1}} \right)}}{\rm{d}}{y_1}} - \frac{{2(1 + \mu )qKy}}{A} $ | (6) |
| $ K = \frac{A}{{{I^2}}}\int_A y \left[ {\int_0^y {\frac{{{S^*}{\rm{d}}{y_1}}}{{b\left( {{y_1}} \right)}}} } \right]{\rm{d}}A $ | (7) |
式中:K为截面特征无量纲数;M为横截面上的弯矩;E为材料弹性模量;G为剪切模量;μ为泊松比;q为梁上分布荷载,以向下为正; A为截面面积。式(6)中后两项即为材料力学法推得的不同步翘曲项。
文献[10]利用弹性力学半逆解法,通过分离工字形截面腹板和翼缘并合理假设边界条件,分别研究腹板和翼缘的受力机理,得到相应的弹性力学法正应力计算公式,并给出支座形式为简支时工字梁水平纤维间挤压应力为:
| $ \begin{array}{l} {\sigma _y} = {a_1}{y^3} + {a_2}{y^2} + {a_3}y + {a_4}\\ \left\{ {\begin{array}{*{20}{l}} {{a_1} = \frac{q}{{I{h^3}}}\left[ {h\left( {{S_2} + {S_1}} \right) - 2I} \right]}\\ {{a_2} = \frac{q}{{2I{h^2}}}\left\{ {h\left[ {\left( {{S_2} - {S_1}} \right) - 3\left( {{\alpha _2} - {\alpha _1}} \right)\left( {{S_1} + {S_2}} \right)} \right] + 6I\left( {{\alpha _2} - {\alpha _1}} \right)} \right\}}\\ {{a_3} = \frac{q}{{Ih}}\left\{ {{S_2}h - {\alpha _2}h\left[ {3{\alpha _1}\left( {{S_1} + {S_2}} \right) + \left( {{S_2} - {S_1}} \right)} \right] + 6I{\alpha _1}{\alpha _2}} \right\}}\\ {{a_4} = \frac{q}{{2h}}\left\{ {\alpha _2^2h\left[ {\left( {{\alpha _2} + 3{\alpha _1}} \right)\left( {{S_1} + {S_2}} \right)} \right]} \right\}} \end{array}} \right. \end{array} $ | (8) |
式中:S1,S2分别为上下翼缘对中性轴面积距的绝对值。
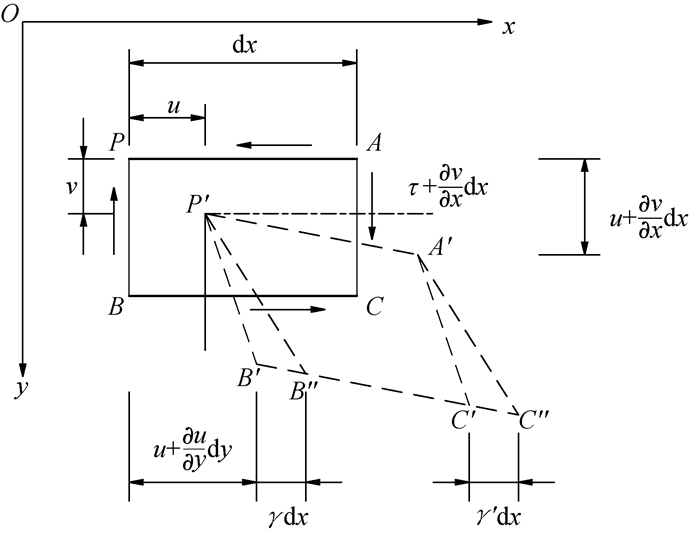
2.1 考虑同步翘曲的正应力在以上研究的基础上构建受剪力情况下微元体变形模型,如图 3所示。
|
图 3 微元体剪切变形 Fig.3 Shear deformation of element |
现取梁上长为dx的微段,其中P点在中性层上,沿x轴和y轴的正方向取两个微小长度的线段PA=dx和PB=dy,并以此围成微元体PACB;假定微元体受剪力,其剪力以引起梁段左边向上和右边向下的变形为正,弯矩以使梁端产生向下凸出的变形为正。设截面的同一高度上剪应力相等,可得剪应力公式为:
| $ \tau = \frac{{Q{S^*}}}{{I{b_{(y)}}}} $ | (9) |
微元体受剪力后,P,A,B三点分别移动到P′,A′,B′,设P点在x方向的位移分量为u,在y方向的位移分量为v,则切应变γ为:
| $ \gamma = \frac{\tau }{G} = \frac{{\partial u}}{{\partial y}} + \frac{{\partial v}}{{\partial x}} $ | (10) |
设梁截面没有平面内的变形,于是v与y无关,它代表梁轴线的挠度。式(7)对y积分得:
| $ u = - \frac{{{\rm{d}}v}}{{{\rm{d}}x}}y + \frac{{QS}}{{I{b_{(y)}}}}y + C(x) $ | (11) |
在中性轴处由u|y=0=0的条件得:
| $ {C_1}(x) = 0 $ | (12) |
在腹板与翼缘相交处横向位移相同,即${\left. {{u_1}} \right|_{y = {h_0}/2}} = {\left. {{u_2}} \right|_{y = {h_0}/2}}$,得:
| $ {C_2}(x) = \frac{{12Q{\beta _2}\alpha _2^2}}{{\left( {1 + 12{\beta _1}\alpha _1^2 + 12{\beta _2}\alpha _2^2} \right)G\delta }} - \frac{{Q\alpha _2^3{h_0}\left( {{h^2} - h_0^2} \right)}}{{2IG}} $ | (13) |
相应的应变为:
| $ {\varepsilon _x} = \frac{{{\rm{d}}u}}{{{\rm{d}}x}} = - \frac{{{{\rm{d}}^2}v}}{{{\rm{d}}{x^2}}}y + \frac{{qS}}{{I{b_{(y)}}}}y + C'(x) $ | (14) |
根据纵向层之间没有正应力的假设,可得正应力为:
| $ {\sigma _{\rm{M}}} = E{\varepsilon _x} = E\left( { - \frac{{{{\rm{d}}^2}w}}{{{\rm{d}}{x^2}}}y + \frac{{qS}}{{I{b_{(y)}}}}y + C'(x)} \right) $ | (15) |
静力学条件为:
| $ M = \int_A {y{\sigma _{\rm M}}{\rm{d}}A} $ | (16) |
将式(12)代入式(13)得:
| $ - \frac{{{{\rm{d}}^2}w}}{{{\rm{d}}{x^2}}} = \frac{M}{{EI}} - \frac{{{b_1}}}{{{I^2}G}}\left[ \begin{array}{l} \frac{{q{h^5}\left( {\alpha _1^5 + \theta \alpha _2^5} \right)}}{{15}} + \frac{{h_0^3{h^2}q\left( {\alpha _1^4{\beta _1} + \theta \alpha _2^4{\beta _2}} \right)}}{2} - \frac{{q{h^2}h_0^3\left( {\alpha _1^4 + \theta \alpha _2^4} \right)}}{6} - \\ \frac{{2qh_0^5\left( {{\beta _1}\alpha _1^5 + \theta {\beta _2}\alpha _2^5} \right)}}{5} + \frac{{q{h_0}{{\left( {{h^2} - h_0^2} \right)}^2}\left( {\alpha _1^5 + \theta \alpha _2^5} \right)}}{4} - \\ \frac{{4q{A_f}h_0^4\left( {{\beta _1}\alpha _1^4 + {\beta _2}\alpha _2^4} \right) + 0.8\delta qh_0^5\left( {\alpha _1^5 + \alpha _2^5} \right)}}{{12{I^2}G}} \end{array} \right] $ | (17) |
将式(17)代入式(15)即可得正应力σM。以上求解过程不作平截面和纵向纤维无挤压假设,其剪力引起的截面翘曲没有考虑相邻剪力的变化,即仅考虑同步翘曲影响。
2.2 不同步翘曲对正应力影响根据图 3,在均布荷载作用下,微元体两端剪力不等。纤维的不同步纵向变形使得B′,C′移动到B″,C″,从而相邻截面的不同步翘曲所引起的正应力为[9]:
| $ {\sigma _{\rm{Q}}} = \frac{{2(1 + \mu )q}}{I}\int_{\min } {\frac{{{S^*}}}{{b\left( {{y_1}} \right)}}} {\rm{d}}{y_1} - \frac{{2(1 + \mu )qKy}}{A} $ | (18) |
在考虑同步翘曲、不同步翘曲影响的基础上,还必须考虑水平纤维间挤压力影响,即添加附加挤压正应力,其中简支工字梁水平纤维挤压应力如式(7)。但需要注意的是,式(7)基于弹性力学假定,σy不随梁长变化。这与文献[3]中越靠近支座处挤压力越明显的描述不符。故假定:①支座截面σys与跨中截面σy之差Δσy按二次抛物线分布;②在跨中处σy沿截面高度按正弦曲线分布,从而对式(7)进一步修正,得到随梁高及梁长(l)变化的挤压正应力,其中修正项为:
| $ \Delta {\sigma _y}(x) = \frac{{12}}{{{l^2}}}\left( {q - {\sigma _y}} \right)\left( {{x^2} - \frac{{{l^2}}}{4}} \right) $ | (19) |
根据纵向线应变与横向线应变的比例关系,推得挤压正应力附加项为:
| $ {\sigma _{\rm{J}}} = - \mu \left( {{\sigma _y} + \Delta {\sigma _y}} \right) $ | (20) |
综上,考虑弯剪耦合及挤压效应求得的单轴对称工字形截面正应力最终表达式为:
| $ {\sigma _x} = {\sigma _{\rm{M}}} + {\sigma _{\rm{Q}}} + {\sigma _{\rm{J}}} $ | (21) |
为了便于分析并使计算式更加简明通用,引入无量纲位置参数:剪高比ξ=2y/h,剪跨比η=x/l,跨高比α=l/h[11],则上下翼缘处弯应力σxw的表达式可统一写为:
| $ {\sigma _{x{\rm{w}}}} = \frac{{3q{\alpha ^2}\eta (1 - \eta )}}{{\delta (1 + 6\beta )}}\left( {1 - {\lambda _{\rm{w}}}} \right) $ | (22) |
中性轴上下腹板处弯应力σxs的表达式可统一写为:
| $ {\sigma _{x{\rm{s}}}} = \frac{{3q{\alpha ^2}\eta (1 - \eta )}}{{\delta (1 + 6\beta )}}\left( {1 + {\lambda _s}} \right) $ | (23) |
引入无量纲由翘曲与挤压引起的影响系数λ,翼缘处为:
| $ \begin{array}{*{20}{c}} {{\lambda _{\rm{w}}} = \mp \frac{{\left( {2\beta + 0.2 + 12{\beta ^2}} \right)(1 + \mu )}}{{\eta (1 - \eta ){\alpha ^2}(1 + 6\beta )}} \pm \frac{{\left( {8\beta + 0.5 - \frac{{{\xi ^2}}}{6} + 2\frac{\beta }{\xi }} \right)(1 + \mu )}}{{\eta (1 - \eta ){\alpha ^2}}} \pm }\\ {\frac{{1 + 6\beta }}{{100\eta (1 - \eta ){\alpha ^2}}}\left\{ {12{\eta ^2} - 3 + \left( {12{\eta ^2} - 4} \right)\left[ {\frac{{{{(\xi + 1)}^3}}}{{4(1 + 6\beta )}} - \frac{{3q(1 + 4\beta )}}{{4(1 + 6\beta )}}(\xi + 1) + 0.5} \right]} \right\}} \end{array} $ | (24) |
腹板处为:
| $ \begin{array}{*{20}{c}} {{\lambda _{\rm{s}}} = \mp \frac{{\left( {2\beta + 0.2 + 12{\beta ^2}} \right)(1 + \mu )}}{{\eta (1 - \eta ){\alpha ^2}(1 + 6\beta )}} \pm \frac{{\left( {2\beta + 0.5 - \frac{{{\xi ^2}}}{6} + 4\frac{\beta }{\xi }} \right)(1 + \mu )}}{{\eta (1 - \eta ){\alpha ^2}}} \pm }\\ {\frac{{1 + 6\beta }}{{100\eta (1 - \eta ){\alpha ^2}}}\left\{ {12{\eta ^2} - 3 + \left( {12{\eta ^2} - 4} \right)\left[ {\frac{{{{(\xi + 1)}^3}}}{{4(1 + 6\beta )}} - \frac{{3q(1 + 4\beta )}}{{4(1 + 6\beta )}}(\xi + 1) + 0.5} \right]} \right\}} \end{array} $ | (25) |
λ的影响因素有跨高比α、剪高比ξ(-1≤ξ≤l)、剪跨比η(0≤η≤l)及翼缘与腹板面积比β。由于在计算式的推导过程中考虑了截面形式、跨高比、横截面翘曲、纵向纤维相互挤压及弯剪耦合效应等问题,因而计算式具有通用性。
4 计算结果对比分析 4.1 计算式无量纲化对比分析表 1中的FEM, DB1, DB2及DB3分别是双轴对称工字形简支梁在不同跨高比和不同翼缘与面积比下正应力有限元解、本文解、文献[9]及[10]解与欧拉细长梁解σ′(y)的比值,用k表示,其中k=σ(y)/σ′(y)。从表 1的数据可发现,随着β的增大,欧拉细长梁解的误差不断增大;当β<0.5时,欧拉细长梁解的误差小于10%,在合理范围之内。为进一步分析各计算方法适用范围,翼缘与腹板面积比取0.5~0.9,跨高比选取工程中深梁通常使用的3~8。
| 表 1 跨中截面不同方法解与欧拉细长梁解的比值 Tab.1 Ratios between solutions of different methods to solution of Bernoulli-Euler slender beam |
与有限元模拟结果对比分析,可得:①随着跨高比的减小和翼缘与腹板面积比的增大,传统欧拉细长梁解的误差逐渐增大。当跨高比较小时,翼缘处正应力误差远大于腹板处,所以跨中截面翼缘处正应力是主要考察范围;②本文解最大误差为5.69%,文献[9]解的最大误差为9.32%,欧拉细长梁解的最大误差为18.70%,其中在跨中截面弯矩正应力最大处不同跨高比与翼缘与腹板面积比的本文解误差均小于文献[9]的误差,本文解更为精确,而文献[10]在跨高比小于5时误差极大。在跨高比6~8时,误差在合理范围内,最大误差为6.89%,计算结果偏于安全。
4.2 算例与分析设有简支工字形截面深梁,长2.50 m,高0.63 m,受均布荷载q=10 kN/m的作用,如图 2。b1=b2=0.180 m,h0=0.586 m。材料为Q235钢,弹性模量E=2.06×108 kPa,泊松比μ=0.30。
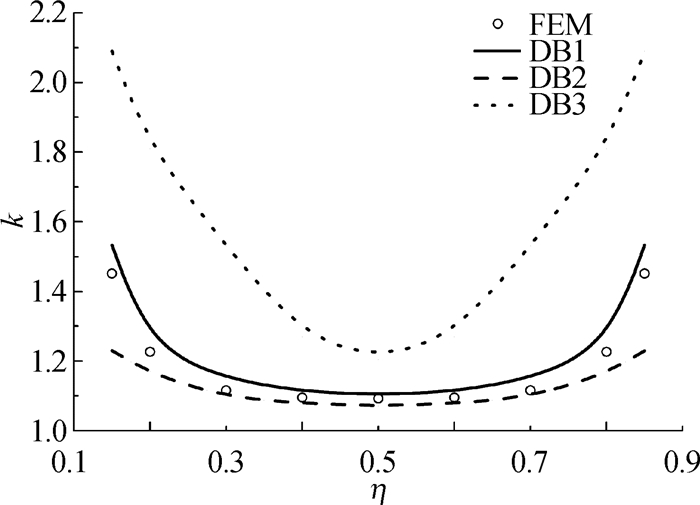
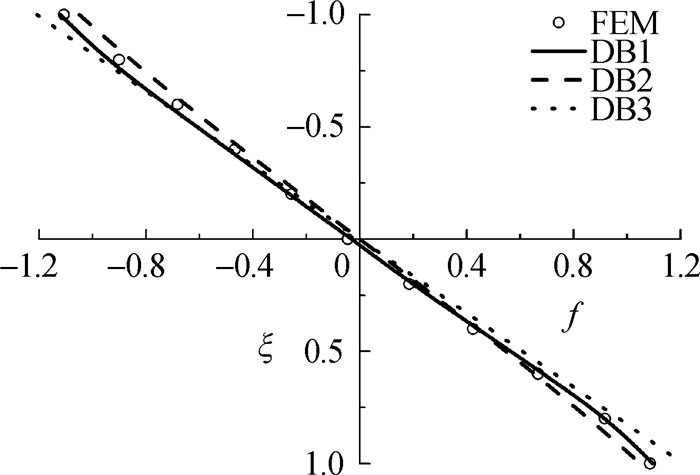
为进一步研究正应力分布规律,利用有限元软件计算出翼缘底部不同方法解的无量纲正应力k沿梁长的变化规律(见图 4)。跨中截面不同方法解的无量纲正应力f沿梁高的变化规律见图 5。其中f=σ(y)/σ′(y)max。
|
图 4 k-η 关系 Fig.4 Relationships between k and η |
|
图 5 f-ξ 关系 Fig.5 Relationships between f and ξ |
分析图 4和5可见:(1)本文解可以很好地描述沿梁长方向的正应力变化规律,最大误差5.5%,跨中截面处误差1.0%,偏于安全;文献[9]给出的解在远离支座时,精度较高,靠近支座时精度不能满足要求,最大误差44.1%,跨中截面处误差1.9%;而文献[10]给出的解,沿跨中截面向支座两端误差逐渐增大,不宜描述不同剪跨比时正应力沿梁长的变化规律,其中跨中截面误差为10.3%;(2)文献[9]和[10]没有考虑挤压影响,正应力近似于线性分布。本文解考虑挤压影响,从图 5可见中性轴略向下移动,符合文献[3]中描述的正应力沿梁高变化规律,最大误差为5.2%。但跨中截面处中性轴下移较小,从图 5可见,文献[9]和[10]在不考虑中性轴下移情况下,依然能定性描述正应力梁高方向的变化规律,文献误差为22.2%,文献精度为31.7%,其误差主要在中性轴下沉处。
5 结语在文献[9]和文献[10]的基础上,考虑同步翘曲、不同步翘曲及挤压对正应力的影响,基于叠加思想改进了以往解析计算方法。通过不同计算方法比较表明:在工字形截面计算时本文解能有效反映正应力变化规律,且计算精度和适用范围优于文献[9]和[10]。同时采用叠加思想和材料力学方法,相比于弹性力学解法更易于分析各类特殊薄壁深梁截面,并能保证其计算精度。
| [1] |
王正中, 朱军祚, 谌磊, 等. 集中力作用下深梁弯剪耦合变形应力计算方法[J]. 工程力学, 2008, 25(4): 115-120. ( WANG Zhengzhong, ZHU Junzuo, CHEN Lei, et al. The stress calculation method for deep beams with shear-bending coupling distortion under concentrated load[J]. Engineering Mechanics, 2008, 25(4): 115-120. (in Chinese)) |
| [2] |
铁摩辛柯.高等材料力学.汪一麟, 译.北京: 科学出版社, 1964. (TIMOSHENKO S. Advanced mechanic of material. Trunslated by WANG Yilin. Beijing: Science Press, 1964. (in Chinese))
|
| [3] |
丁大钧, 刘伟庆. 深梁杆件力学解[J]. 工程力学, 1993, 10(1): 10-18. ( DING Dajun, LIU Weiqing. Solution of deep beams based on mechanics of bar system[J]. Engineering Mechanics, 1993, 10(1): 10-18. (in Chinese)) |
| [4] |
王桂芳. 简支深梁的应力分析[J]. 成都科技大学学报, 1993, 70(3): 70-76. ( WANG Guifang. Stress analysis of simply support deep beams[J]. Journal of Chengdu University of Science and Technology, 1993, 70(3): 70-76. (in Chinese)) |
| [5] |
杨伯源, 巫绪涛, 李和平. 剪切弯曲下短深梁位移数值计算精度的研究[J]. 应用力学学报, 2003, 20(2): 145-146. ( YANG Boyuan, WU Xutao, LI Heping. Research on the precision of the numerical calculation of the displacement of short or deep beams with shear and bending[J]. Chinese Journal of Applied Mechanics, 2003, 20(2): 145-146. DOI:10.3969/j.issn.1000-4939.2003.02.033 (in Chinese)) |
| [6] |
梅甫良, 曾德顺. 深梁的精确解[J]. 力学与实践, 2002, 24(3): 58-60. ( MEI Fuliang, ZENG Deshun. Precise solution of deep beams[J]. Mechanics and Practice, 2002, 24(3): 58-60. DOI:10.3969/j.issn.1000-0879.2002.03.021 (in Chinese)) |
| [7] |
舒小娟, 钟新谷, 沈明燕, 等. 基于剪切变形的矩形梁剪力滞求解方法[J]. 计算力学学报, 2015(4): 518-522. ( SHU Xiaojuan, ZHONG Xingu, SHEN Mingyan, et al. Calculation method for shear lag of rectangular section beam based on the shear deformation[J]. Chinese Journal of Computational Mechanics, 2015(4): 518-522. (in Chinese)) |
| [8] |
WU Siyuan. Analytical solutions for wide flange I-shaped deep beam with shear effect of whole section, November 22-24, 2018 //Kyoto: The Thirty-First KKHTCNN Symposium on Civil Engineering, 2018.
|
| [9] |
王正中, 沙际德. 深孔钢闸门主梁横力弯曲正应力与挠度计算[J]. 水利学报, 1995(9): 40-46, 24. ( WANG Zhengzhong, SHA Jide. Calculation of normal stress and deflection in transverse bending of main beam in outlet gate[J]. Journal of Hydraulic Engineering, 1995(9): 40-46, 24. DOI:10.3321/j.issn:0559-9350.1995.09.006 (in Chinese)) |
| [10] |
王正中, 刘计良, 牟声远, 等. 深孔平面钢闸门主梁应力计算方法研究[J]. 水力发电学报, 2010, 29(3): 170-176. ( WANG Zhengzhong, LIU Jiliang, MOU Shengyuan, et al. Research on stress calculation method for main beam of plain steel gate in deepwater delivery structure[J]. Journal of Hydroelectric Engineering, 2010, 29(3): 170-176. (in Chinese)) |
| [11] |
刘计良, 王正中, 韩彦宝, 等. 均布荷载作用下工字形截面单跨超静定深梁应力计算方法研究[J]. 工程力学, 2010, 27(3): 174-179. ( LIU Jiliang, WANG Zhengzhong, HAN Yanbao, et al. Study on stress calculation method for hyperstatic deep beams with single span and I section subjected to uniform load[J]. Engineering Mechanics, 2010, 27(3): 174-179. (in Chinese)) |
| [12] |
李尧臣. 梁的弯曲正应力的材料力学方法修正[J]. 力学与实践, 2006, 28(2): 73-74. ( LI Yaochen. A correctional beam bending normal stress of the material mechanics method[J]. Mechanics in Engineering, 2006, 28(2): 73-74. DOI:10.3969/j.issn.1000-0879.2006.02.017 (in Chinese)) |
2. College of Civil Engineering, Tongji University, Shanghai 200092, China;
3. Shanghai Thousand Year Design Co., Ltd., Shanghai 201108, China
 2019
2019 
