底部加热两平板之间的对流问题被称为Rayleigh-Benard对流。关于这个问题的研究已有一百多年历史，从最初的试验研究，理论分析到近几十年的数值模拟，研究工作一直吸引着科研人员的兴趣^[1-5]。数值模拟可分为基于简单振幅方程组或模型方程组的数值模拟，利用扰动方程组的模拟，以及利用流体力学方程组的数值模拟。特别是基于流体力学方程组的数值模拟大大推动了Rayleigh-Benard对流的研究，揭示了许多新的现象。例如，对于混合流体，腔体中出现的行波、局部行波、具有不同结构的对流行波解等。这些都是在单流体下没有观察到的。数值模拟的一个优点是通过模拟可以获得Rayleigh-Benard对流的微细结构，这是实验中很难测量与观测的现象。因此，数值模拟已成为研究底部加热两平板之间对流问题的有力工具。

给底部加热两板之间的对流施加一个水平流动，形成一个新的对流系统^[6-10]，导致许多新现象的产生^[11-14]。对该系统的研究已获得许多进展，但仍然有许多问题需要进一步深入研究。本文采用二维流体力学基本方程组对普朗特数Pr=0.72的具有水平流动的底部加热两板之间的流动特性进行数值模拟。

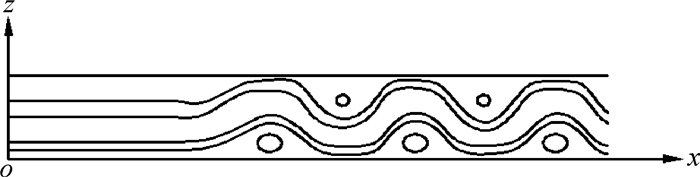
1 水平流动进口段及其数学模型 1.1 水平流动进口段

首先讨论具有水平流动的底部加热两板之间的流动问题。当底部加热两板之间的温度差超过临界值时，底部加热两板之间发生对流现象，即在底部加热两板之间发生对流滚动。对于纯流体，这种对流滚动是定常的。如果给底部加热两板之间的对流施加一个水平流动，由于水平流动与底部加热两板之间的对流或者说底部加热两板之间温度差的热作用的竞争，导致两板之间出现复杂的对流斑图。在两板之间温度差与水平流动强度的某种组合下，系统中可能发生均匀行波对流或水平流动控制局面的现象。当两板之间温度差与水平流动强度在合适的参数范围时，两板之间发生水平流动与对流滚动联合出现的现象，即局部行波对流。也就是说，两板之间的上游区由水平流动控制，下游区则由行波对流滚动支配。将两板之间的上游区水平流动控制段称为水平流动进口段，如图 1所示。水平流动进口段长度依赖于水平流动强度和两板之间温差变化。

1.2 数学模型 1.2.1 控制方程组

对于图 1所示流动斑图，考虑Boussinesq假定，密度变化为ρ=ρ₀[1-α(T-T₀)]时，控制流动系统的流体力学方程组为：

$ {\nabla \cdot \mathit{\boldsymbol{U}} = 0} $

(1)

$ {\frac{{\partial \mathit{\boldsymbol{U}}}}{{\partial t}} + (\mathit{\boldsymbol{U}} \cdot \nabla )\mathit{\boldsymbol{U}} = - \nabla \frac{p}{{{\rho _0}}} + \nu {\nabla ^2}\mathit{\boldsymbol{U}} - \alpha \left( {T - {T_0}} \right)\mathit{\boldsymbol{g}}} $

(2)

$ {\frac{{\partial T}}{{\partial t}} + (\mathit{\boldsymbol{U}} \cdot \nabla )T = \kappa {\nabla ^2}T} $

(3)

式中：$\mathit{\boldsymbol{U}}\left({u, 0, w} \right)$为速度矢量场; p为压强; ρ为密度; T为温度; ν为运动黏性系数; α为体积膨胀系数，$\alpha = - \frac{1}{{{\rho _0}}}\frac{{\partial \rho (T, p)}}{{\partial T}}$; t为时间; κ为热扩散系数，$\kappa=\frac{\lambda}{\rho_{0} C_{\mathrm{p}}}$，C_p为比热，λ为热传导系数; $\mathit{\boldsymbol{g}} = - g{\mathit{\boldsymbol{e}}_z}$，g为重力加速度，e_z为z方向单位矢量。下标为0表示相应物理量的参考值。

这个流动系统由以下几个参数控制，表征温度差的瑞利数$Ra = \frac{{\alpha g{d^3}}}{{\kappa \nu }}\Delta T$，一般用相对瑞利数为r=Ra/Ra_c来表示，临界值Ra_c=1 708;表征水平流动强度的雷诺数$\mathit{Re = }\frac{{{u_{\max }}d}}{\nu }$; 表示流体物性的普朗特数Pr=ν/κ。其中，d为腔体高度; ΔT为温度差，ΔT=T_d－T_u，T_d为下部平板温度，T_u为上部平板温度; u_max为水平流动最大流速。

1.2.2 边界条件和初始条件

上下壁面的流速为：在z=0，d时，u=w=0。上下壁面温度恒定，即在z=0时，T=T_d; 在z=d时，T=T_u。

左端部进口条件为：在x=0时，$u = 4{u_{\max }}\frac{z}{d}\left({1 - \frac{z}{d}} \right), w = 0, T = {T_0} + \mathit{\Delta }T\left({0.5 - \frac{z}{d}} \right)$; 在x=L_x时，右端部出口为自由出流，L_x为腔体长度。

流速初始条件为：u=w=0，初始温度取平均值(一般T=293.15K)。

1.2.3 数值计算方法

根据有限容积法对流体力学基本方程组进行离散，采用SIMPLE算法对速度-压力方程进行数值求解。文献[9]对d/20和d/30两种网格的比较说明最大垂直流速很接近，因此，采用d/20的网格。时间步长采用Δt=0.01 s。为方便说明，坐标无量纲化为X=x/d, Z=z/d。模拟采用的普朗特数Pr=0.72，腔体长高比Γ=L_x/d=12。

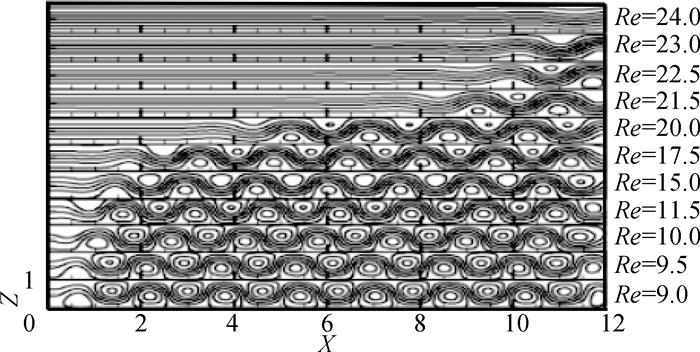
2 水平流动进口段长度 2.1 底部加热两板之间的3种流动斑图

具有水平流动的底部加热两板之间的流动斑图依赖于表征水平流动强度的雷诺数Re和表征两板之间温度差大小的相对瑞利数r。对于给定的相对瑞利数，水平流动雷诺数Re的大小将决定具有水平流动进口段长度的对流斑图。图 2给出了相对瑞利数r=4情况下，不同水平流动雷诺数Re时具有水平流动的底部加热两板之间的流动斑图。每个框子内为流动稳定时两板之间的流线图，水平流动雷诺数向上增大，对应的流动斑图也发生变化。可以看出，当水平流动雷诺数Re≤9.5时，两板之间是基本均匀的行波对流。这时，由于水平流动雷诺数较小，两板之间热作用抑制了水平流动，控制了整个腔体，两板之间热作用和水平流动的平衡导致形成充满两板之间的行波对流。在长高比Γ=12的腔体中，存在15个滚动，其平均波数k=15π/12=3.93。当水平流动雷诺数超过Re=9.5时，两板之间出现具有水平流动进口段的局部行波对流。当水平流动雷诺数Re=17.5时，水平流动进口段长度X₀=1.5，在1.5≤X≤12.0的范围内是行波对流，行波对流的平均波数为k=13π/10.5=3.89。这时，水平流动强度已增大到在进口段范围抑制两板之间热作用，从而形成水平流动进口段长度; 而在1.5≤X≤12.0的区间，两板之间热作用和水平流动的平衡导致形成两板之间的行波对流。因此，两板之间是具有水平流动进口段的局部行波对流。当水平来流雷诺数进一步增到Re≥24.0时，水平流动强度已增大到在整个腔体范围抑制两板之间热作用，对流滚动消失，从而形成水平流动。总之，随着参数变化，两板之间出现3种流动斑图。在水平流动雷诺数9.5＜Re＜24.0的范围内存在水平流动进口段，水平流动进口段长度取决于水平流动雷诺数的大小。

2.2 水平流动进口段长度对雷诺数的依赖性

水平流动雷诺数影响着水平流动进口段长度。对于给定的相对瑞利数r=3时，雷诺数Re为9.0，10.0，14.0，15.0，17.0，19.0，20.0和21.0，两板之间的水平流动进口段长度X₀为0，0.5，1.0，1.5，5.0，10.5，11.0和12.0。对以上数据进行拟合分析(图 3)，可得水平流动进口段长与雷诺数的相关关系式为：

$ {X_0} = 0.120\mathit{R}{\mathit{e}^2} - 2.507\mathit{Re} + 13.031 $

(1)

式中: Re可变范围为9.0≤Re≤21.0，可决系数R²=0.966 9。

当水平流动雷诺数Re≤9.0时，两板之间的水平流动进口段长度X₀=0，系统是均匀行波对流状态。当水平流动雷诺数Re≥21.0时，两板之间的水平流动进口段长度X₀=12.0，系统是水平流动状态。在水平流动雷诺数9.0＜Re＜21.0时，系统具有水平流动的底部加热两板之间的局部行波流动斑图，存在两板之间的水平流动进口段。两板之间的水平流动进口段长度随水平流动雷诺数的增加而增加。这是因为对于给定的相对瑞利数或者说温度差的热作用，随着水平流动雷诺数增加，水平流动抑制温度差热作用的能力加强，因此，水平流动进口段范围扩大。

2.3 水平流动进口段长度对相对瑞利数的依赖性

相对瑞利数是两板之间温度差热作用的反映，它影响着水平流动进口段长度。对于给定的水平流动雷诺数Re=25.0时，当相对瑞利数r为4，5，6，7，8，9，10和12时，两板之间水平流动进口段长度分别为12.0，8.5，4.5，1.5，1.2，1.0，0.5和0。对以上数据进行相关分析(图 4)，可得水平流动进口段长度与相对瑞利数的变化关系式为：

$ X_{0}=-0.046 r^{3}+1.417 r^{2}-14.667 r+51.327 $

(2)

式中：r的可变化范围为4≤r≤12，可决系数R²=0.987 5。

可以看出，当相对瑞利数r≤4时，两板之间水平流动进口段长度X₀=12.0，水平流动控制整个腔体。当相对瑞利数r≥12时，两板之间水平流动进口段长度X₀=0，两板之间充满对流滚动的行波对流。在相对瑞利数4＜r＜12的范围内，两板之间是局部行波流动斑图，出现两板之间的水平流动进口段。两板之间水平流动进口段长度随相对瑞利数的增加而减小。这是因为对于给定的水平流动雷诺数，随着相对瑞利数的增加两板之间温度差的热作用增强，导致对流能力增强，因此，行波对流滚动区间变大，水平流动区间减小。

3 结语

采用二维流体力学基本方程组对普朗特数Pr=0.72的具有水平流动的底部加热两板之间的流动特性进行数值模拟，得出以下结论：

(1) 对于给定相对瑞利数r，随着雷诺数Re由零开始增加，具有水平流动的底部加热两板之间依次出现定常对流滚动，均匀行波对流滚动，具有水平流动进口段的局部行波对流滚动及水平流动斑图等。

(2) 当相对瑞利数r=3时，在雷诺数9.0＜Re＜21.0的范围内，系统是局部行波对流滚动，存在水平流动进口段。随着水平流动雷诺数增加，水平流动抑制温度差热作用的能力加强，因此，水平流动进口段范围扩大。

(3) 当雷诺数Re=25.0时，在相对瑞利数4＜r＜12的范围内，两板之间是局部行波对流滚动，出现水平流动进口段。随着相对瑞利数的增加，两板之间温度差的热作用增强，导致对流能力增强，因此，行波对流滚动区间变大，水平流动区间减小。