2. 东南大学 交通学院 港航工程系,江苏 南京 210096
内河航道服务区是沿航道布置的通航辅助设施,类似于高速公路服务区,为过往船舶和船员提供锚泊和补给服务,解决船舶靠泊难、过夜难、补给难等突出问题,在保障航行安全和提升内河水运服务品质等方面发挥了重要作用[1]。服务区建设规模是其规划设计的关键问题之一。为协调船舶的服务“需求”和服务区的服务“供给”,需要合理确定航道服务区水域规模,即能同时容纳接受服务的最大船舶数量或服务区水域面积[2-3]。通常,根据航道船舶流量、船舶服务需求概率(驶入率)、服务时间(泊位周转率)等,可算出服务区所需水域面积或泊位数量[4-5]。
由于航道上的船舶受到人、货、船等多种因素的影响,服务区水域面积的计算参数均是随机变量,经验公式中往往只能给出取值范围,使得计算结果有较大不确定性。如根据经验公式[4-5],在同一船舶流量下,因参数取值不同,计算得到的泊位数量可相差2~4倍[6]。若采用交通建模仿真方法来模拟船舶行为,则能较好地描述并分析这类动态交通系统[7-8]。常用的船舶交通建模方法有模拟随机过程的蒙特卡罗法[9]、基于离散事件仿真平台的建模方法[10],将空间看作离散元胞按规则演化的元胞自动机方法[11]、采用具有自我控制、环境反应和交互协作等特性的智能体方法[12]等。其中,基于AnyLogic的多智能体仿真可充分利用智能体间的自治、推理、通讯和协作机制,模拟个体间相互独立又交互作用的现象[13],非常适合分析涉及众多随机因素的交通现象。因此,本文基于AnyLogic仿真平台,在文献[1]的基础上,根据船舶交通流特征等建立内河航道服务区水域面积的仿真模型,分析服务区水域面积的计算方法,供相关规划和设计参考。
1 交通建模交通建模就是模拟船舶到达并驶入服务区,获得服务后驶出服务区的全过程,通过记录相关数据以统计分析服务区所需的最大泊位数或水域面积。该离散事件系统包含两个实体:服务区泊位和船舶。其中,船舶具有服务需求类别、尺寸、船员数量等属性,服从随机分布。该系统主要涉及3个变量:(1)船舶到达间隔I,即航道中两艘相邻船舶到达服务区的间隔时间; (2)服务概率Sp,即当船舶到达服务区后驶入服务区内接受服务的概率; (3)服务时间St,即船舶从驶入服务区到服务完成后驶离服务区的时间间隔。理想状况下,这3个变量决定了服务区内同时接受服务的船舶和船员数量,即同时停泊船舶的最大数量和人员聚集量。
统计分析时,首先由船舶停泊数量和适当的泊位保证率得到所需泊位数量; 然后,由所需泊位数量与单船面积得到船舶总面积,并考虑与船舶停靠方式、掉头等有关的水域安全系数,即可得到所需的水域总面积。此外,根据服务区船员聚集量和单位设施面积,可进一步分析服务区陆上设施所需规模。需要指出的是,服务区船舶的实际交通情况很复杂,为分析服务区船舶停泊状况,考虑了如下简化:(1)服务区可以提供足够多的泊位,船舶到达服务区便能停泊接受服务; (2)服务时间是船舶在服务区内进行多项服务所花费的总时间,仅随服务事件不同而改变,不单独考虑船舶进出服务区耗费的时间; (3)不考虑锚泊水域停泊船舶之间的相互影响以及周边设施的影响。
1.1 模型参数(1) 交通流特征。船舶到达间隔I与船舶流量相关。如低密度交通流时,船舶达到间隔服从负指数分布,对应的船舶流量服从泊松分布。船舶流量是在单位时间内通过航道某一断面的船舶数量,可用艘数、吨位、面积来表示。船舶流量随时间和空间而变化,其分布规律可根据实际调查确定。考虑到船舶日流量的随机性,实际情况下可根据航段的船舶日流量均值确定具有一定保证率的船舶流量设计值[14-15],即
| $ Q_{d}=q \beta_{d} $ | (1) |
式中:Qd为具有d%保证率的船舶日流量; q为船舶日流量均值; βd为保证率为d%的船舶日流量不均衡系数[14-15]。
(2) 船舶特征。因到达船舶的属性(类型、吨位、总长、总宽等)差异很大,为简化问题,将复杂的船型进行统计分类,选取m类代表船舶(代表船型种类越多越接近实际情况)作为仿真模型的输入船舶[10]。第i类船舶的特征向量Vi为:
| $ V_{i}=\left[G_{i}, L_{i}, B_{i}, H_{i}, \phi_{i}\right], i=1, 2, 3, \cdots, m $ | (2) |
式中:Gi为船舶吨位; Li为船舶长度; Bi为船舶宽度; Hi为船员数量; ϕi为船舶所占比例,且∑ϕi=1。代表船舶的尺度可根据统计或抽样资料分析确定。
(3) 服务特征。服务概率Sp和服务时间St主要与服务事件n相关。一般地,第j类服务的特征向量Sj为:
| $ S_{j}=\left[S_{p j}, S_{t j}\right], j=1, 2, 3, \cdots, n $ | (3) |
式中:Spj为第j类服务的服务概率,表示航道中驶入服务区接受服务的船舶百分比,又称驶入率; Stj为第j类服务的服务时间。服务特征可根据实地调研和问卷调查确定,亦可参考相关文献。例如,尽管船舶进入服务区可接受多种服务,根据服务时间可将一系列服务事件分为两类[1-2]:①锚泊类事件,特点是服务时间较长,通常为几小时,甚至几天,在此期间可能使用其他服务; ②补给类事件,特点是服务时间较短,通常在1~2 h内,以补给服务为主,如加油、加气、购物等。
1.2 结果统计如前所述,通过设置仿真时长和仿真次数,可记录仿真得到的服务区停泊船舶数量N、总面积S和船员聚集量M等。显然,N,S,M均为随机变量。以N为例,当得到的样本量y非常大时,根据中心极限定理,其服从正态分布,总体分布的均值μ和标准差σ可采用极大似然估计法通过样本均值和标准差进行估计。若采用极大似然估计法对μ和σ2进行参数估计,总体N的概率密度:
| $ f\left( {N;\mu , {\sigma ^2}} \right) = \frac{1}{{\sqrt {2\pi \sigma } }}\exp \left( { - \frac{{{{(N - \mu )}^2}}}{{2{\sigma ^2}}}} \right), \sigma > 0 $ | (4) |
于是似然函数为:
| $ L\left( {{N_1}, \cdots , {N_y};\mu , {\sigma ^2}} \right) = f\left( {{N_1};\mu , {\sigma ^2}} \right) \cdots f\left( {{N_y};\mu , {\sigma ^2}} \right) = {\left( {2{\rm{ \mathtt{ π} }}{\sigma ^2}} \right)^{ - \frac{y}{2}}}\exp \left( { - \sum\limits_{k = 1}^y {\frac{{{{\left( {{N_k} - \mu } \right)}^2}}}{{2{\sigma ^2}}}} } \right) $ | (5) |
两边取对数得:
| $ \frac{{\partial \ln L}}{{\partial \mu }} = \sum\limits_{k = 1}^y {\frac{{{N_k} - \mu }}{{{\sigma ^2}}}} = 0, \frac{{\partial \ln L}}{{\partial {\sigma ^2}}} = - \frac{y}{{2{\sigma ^2}}} + \frac{1}{{2{\sigma ^4}}}\sum\limits_{k = 1}^y {{{\left( {{N_k} - \mu } \right)}^2}} = 0 $ | (6) |
即,μ和σ2的极大似然估计为样本均值
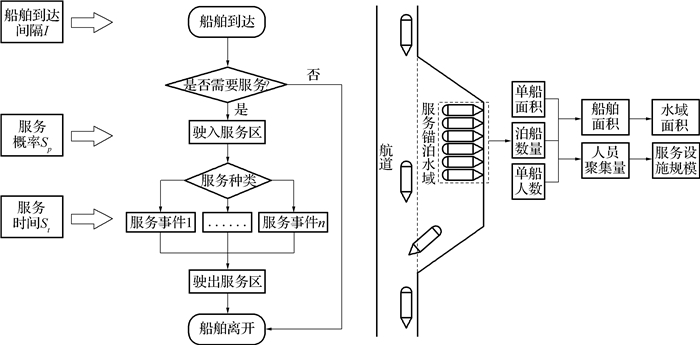
AnyLogic是最早引入统一建模语言的系统建模和仿真工具,支持多智能体、离散事件和系统动力学等多种建模方法。AnyLogic拥有丰富的建模库件,完全基于Java语言开发,拥有强大的二次开发能力,已广泛应用供应链物流、交通、公共管理等复杂系统的建模与仿真[16]。图 1给出了航道服务区交通仿真的AnyLogic仿真流程图,包括服务区及上下游航段的水域,考虑锚泊类、补给类两类服务事件,船舶交通流特征和服务特征参数均在判断模块赋值,仿真结果统计主要在接受服务模块。
|
图 1 AnyLogic仿真流程 Fig.1 Flow chart of traffic simulation of IWSA based on AnyLogic |
设置仿真时长30 d,重复运行仿真30次,每隔1 min分别记录服务区内的N,S,M值。总计可得到129.6万个样本。
2.2 结果验证以长三角地区京杭运河无锡新安水上服务区(以下简称新安服务区)、连申线盐城东台水上服务区(以下简称东台服务区)、芜申运河宜兴水上服务区(以下简称宜兴服务区)为例进行仿真试验。这3个服务区均属于综合服务区,为船舶提供锚泊类和补给类服务,基本情况见表 1,其中平均泊船数根据2013—2017年多次谷歌卫星图片进行统计得到[6]。
| 表 1 3个服务区概况 Tab.1 Basic information of three inland waterway service areas |
船舶特征尺寸根据京杭运河标准船型确定,船舶吨位比例根据断面统计数据确定。船舶到达时间间隔根据船舶流量计算得到。根据上述3个服务区进行的问卷调查[6],锚泊类和补给类两类服务事件的服务概率(驶入率)和服务时间的均值分别取为0.10和10 h,0.05和2 h。因未能具体统计分析服务概率和服务时间所遵循的统计规律,先假设均服从泊松分布。
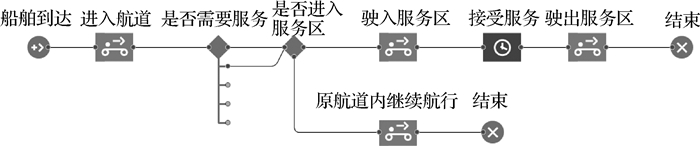
表 2给出了3个服务区所需水域规模的仿真统计结果。为验证该结果的合理性,将仿真平均船舶停泊数N与实际平均停泊数对比; 将船舶总面积S乘以水域安全系数1.05作为仿真水域面积,与实际水域面积对比,如图 2所示。图 2中仿真结果中间长横线为均值μ,上下短横线为均值加减标准差μ±σ,即上、下短线代表的船舶数或水域面积分别具有84.13%和15.87%的保证率。可以看出,实际船舶数和水域面积均位于仿真结果的μ±σ范围内,仿真结果与实际情况吻合,表明该仿真模型及其参数能较好地反映目前航道船舶流量条件下服务区的使用情况。
| 表 2 仿真结果统计 Tab.2 Statistic values of traffic simulation of three inland waterway service areas |
|
图 2 仿真结果验证 Fig.2 Validation of traffic simulation results from three inland waterway service areas |
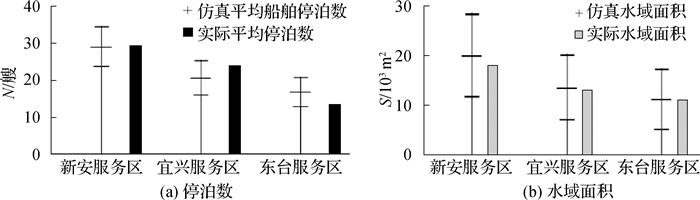
上文服务特征参数均假定为泊松分布,而其实际分布可能有所不同。根据概率理论[17],多次独立伯努利试验成功次数所服从的分布称为二项分布。泊松分布是二项分布样本很大而概率很小时的一种极限形式,泊松过程的事件间隔分布为指数分布,指数分布是许多常见分布的特殊形式,如韦布分布、伽马分布、瑞利分布和贝塔分布等。因此,考虑服务概率和服务时间的多种概率分布情况(图 3),仿真分析并对比结果见表 3。可见,在分布均值相同情况下,服务特征参数的概率分布类型对仿真结果的影响很小。
|
图 3 服务特征参数的不同概率分布 Fig.3 Different probability distributions of service characteristic parameters |
| 表 3 服务特征参数概率分布类型对停泊船舶数量的敏感性分析 Tab.3 Sensitivity analysis of different probability distributions of service characteristic parameters |
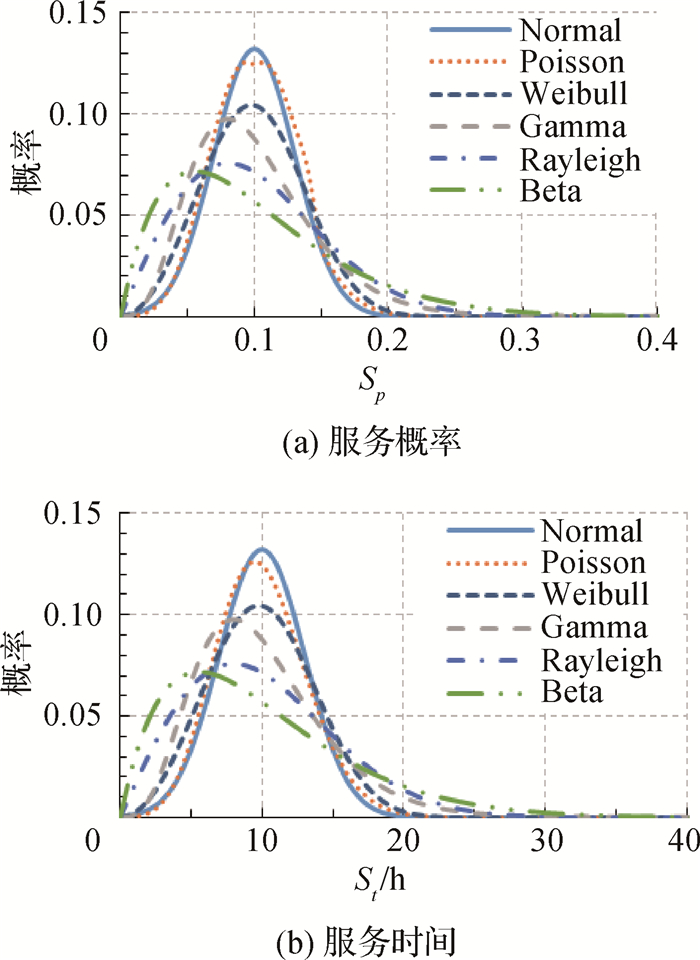
需要特别指出的是,文中服务概率和服务时间的均值根据问卷调查获得,仅代表新安、宜兴和东台等3处服务区的情况,而实际情况下各服务区的服务特征可能不同。为讨论服务特征对仿真结果的影响,进一步改变服务概率和服务时间的均值,统计仿真结果如图 4所示。图中短横线为仿真统计值的均值μ,短竖线上、下限值为μ±σ(相应的保证率为84.13%和15.87%); 虚斜线为均值的线性回归,其斜率分别为283.6和2.6(R2分别为0.997和0.998)。可见,随着服务概率和服务时间的均值变大,服务区停泊船舶数量也将变大,二者接近线性关系。根据该计算条件下(同表 3)的计算结果,服务概率均值每增加0.05,服务区内停泊的船舶数量增加14.2艘; 服务时间均值每增加1 h,船舶数量增加2.6艘,表明服务特征的均值对服务区水域规模是敏感的。可根据现场调查或类似服务区经验给定服务概率Sp和服务时间St的取值范围,如文献[4-5]中推荐Sp取值0.04~0.12, St取值3~4 h。根据调研[6]和文献[1],推荐锚泊类服务的Sp和St取值范围分别为0.10~0.15, 8~12 h,补给类服务的Sp和St取值范围分别为0.05~0.10, 2~4 h。
|
图 4 服务特征参数的均值对停泊船舶数量的敏感性分析 Fig.4 Sensitivity analysis of mean values of service characteristic parameters |
为得到具有实用性的结果,考虑服务区所在航段上不同船舶流量下服务区停泊船舶数量。不妨取流量Qd间隔为50艘/d,锚泊类事件和补给类事件的服务特征参数同前,即其服务概率(驶入率)和服务时间的均值分别取为0.10和10 h, 0.05和2 h,进行多次仿真,结果列于表 4。根据表 4进行回归分析,可知综合服务区停泊船舶数量N与其所在航段上船舶流量近似线性相关:
| 表 4 不同船舶流量下服务区停泊船舶数仿真结果 Tab.4 Simulated results of number of vessels berthing in IWSA at different traffic flow rates |
| $ N=(0.0448 \pm 0.0067) Q_{d} \quad\left(R^{2}=0.999\right) $ | (7) |
式中:0.044 8为均值μ的回归系数, 0.0067为方差σ的回归系数; “+”,“-”分别表示保证率为84.13%和15.87%时的系数取值。
由式(7)可知,尽管服务区水域面积与船舶驶入率、服务时间等复杂因素有关。通过大量仿真结果的统计分析,可将服务区停泊船舶数量简化为相应航道上船舶流量的连续函数。流量每变化100艘/d,泊位数量N取值上下限相差1~2个泊位。服务区水域面积还与航道等级以及航道上的实际船型有关,可进一步根据航段上的船舶平均吨位(与航道等级有关)以及船舶吨位与面积关系,将泊位数量转化为水域面积:
| $ {S^*} = N \times {A_{\rm{v}}} \times \eta $ | (8) |
式中:S*为考虑水域安全系数η的服务区水域面积(m2); Av为船舶平均面积(m2),可根据航段上实际船型或标准船型通过线性或二次多项式回归分析得到[15],如京杭运河标准船型的船舶吨位与面积关系可表示为Av=0.47g+132,g为船舶平均吨位。这样,就可以将服务区水域面积简化为航段上船舶流量和船舶平均吨位的连续函数,有助于方便估算服务区所需的水域面积。
最后指出的是,式(7)或表 4是基于特定航道服务区调研所得的服务特征参数给出的,且假设需要进服务区的船舶均能够进入服务区,是服务区所需水域面积的上限。但实际上受自然条件、营运管理等因素限制,如部分船舶将服务区作为长期锚地(停泊时间大于3 d),挤占了服务区有限的水域资源,许多服务区的水域面积往往并不能满足全部有需求的船舶进入。下一步还可深入分析航道服务区的功能配置、服务区布局选址以及营运管理等问题对服务区建设规模的影响。
4 结语(1) 基于船舶交通流和服务特征,提出了基于交通建模仿真的航道服务区水域面积确定方法,并以新安、宜兴和东台3处服务区为例进行了验证。通过大量仿真和回归分析,可将服务区水域面积简化为航段上船舶流量和船舶平均吨位的连续函数,有助于方便合理地估算服务区所需水域面积。
(2) 仿真模型参数的敏感性分析表明,服务区停泊船舶数量与航段上船舶流量、服务特征参数的均值成线性正比关系,服务特征参数的概率分布类型对仿真结果影响很小。
(3) 本文提出的仿真模型仅针对单个服务区,多个服务区间的相互影响等因素尚未考虑,下一步可深入分析内河航道服务区的功能配置、布局选址、营运管理与建设规模等因素间的相互影响。
| [1] |
廖鹏, 张玮, 姜晔, 等. 江苏干线航道服务区服务需求特征分析[J]. 水运工程, 2008(6): 122-126. ( LIAO Peng, ZHANG Wei, JIANG Ye, et al. Analysis of characteristics of service demand on main inland waterway in Jiangsu province[J]. Port and Waterway Engineering, 2008(6): 122-126. DOI:10.3969/j.issn.1002-4972.2008.06.027 (in Chinese)) |
| [2] |
LIAO P. Service demand forecast for an inland waterway service area: A case study on the Grand Canal, China [C]//Proceeding of the 5th International Conference on Transportation Engineering, September 26-27, 2015, Dalian, China. Reston: ASCE, 2015: 327-334.
|
| [3] |
KOO C, HONG T, KIM J. A decision support system for determining the optimal size of a new expressway service area: Focused on the profitability[J]. Decision Support Systems, 2014, 67: 9-20. DOI:10.1016/j.dss.2014.07.005 |
| [4] |
DB 33/T 845—2011内河航道服务区总体设计规范[S]. (DB 33/T 845—2011 Code for master design of inland channel service area[S]. (in Chinese))
|
| [5] |
DB 32/T 2885—2016内河水上服务区总体设计规范[S]. (DB 32/T 2885—2016 Code for master design of inland waterway service area[S]. (in Chinese))
|
| [6] |
安徽省交通科学研究院, 东南大学.安徽省内河水上服务区(锚地)建设标准化研究[R].合肥: 安徽省交通科学研究院, 2017. (Anhui Transportation Research Institute, Southeast University. Construction standardization research on inland waterway service area (anchorage) in Anhui Province [R]. Hefei: Anhui Transportation Research Institute, 2017. (in Chinese))
|
| [7] |
DAHAL K, GALLOWAY S, BURT G, et al. A port system simulation facility with an optimization capability[J]. International Journal of Computational Intelligence and Applications, 2003, 3(4): 395-410. DOI:10.1142/S1469026803001099 |
| [8] |
徐武雄, 初秀民, 刘兴龙. 船舶交通流建模与仿真研究进展[J]. 水利水运工程学报, 2014(6): 91-99. ( XU Wuxiong, CHU Xiumin, LIU Xinglong. Review of modeling and simulation of vessel traffic flow[J]. Hydro-Science and Engineering, 2014(6): 91-99. DOI:10.3969/j.issn.1009-640X.2014.06.014 (in Chinese)) |
| [9] |
GOERLANDT F, KUJIALA P. Traffic simulation based ship collision probability modeling[J]. Reliability Engineering and System Safety, 2011, 96(1): 91-107. DOI:10.1016/j.ress.2010.09.003 |
| [10] |
孔庄, 廖鹏, 杨春红, 等. 船闸运行状态与通过能力仿真分析[J]. 水利水运工程学报, 2017(1): 73-79. ( KONG Zhuang, LIAO Peng, YANG Chunhong, et al. Analysis of shiplock operation and throughput capacity based on traffic simulation model[J]. Hydro-Science and Engineering, 2017(1): 73-79. (in Chinese)) |
| [11] |
QI L, ZHENG Z Y, GANG L H. A cellular automaton model for ship traffic flow in waterways[J]. Physica A, 2017, 471: 705-717. DOI:10.1016/j.physa.2016.12.028 |
| [12] |
XIAO F, LIGTERINGEN H, VAN GULIJK C, et al. Nautical traffic simulation with multi-agent system for safety[C]//16th International IEEE Conference on Intelligent Transportation Systems(ITSC 2013), October 6-9, 2013. New York: IEEE, 2013: 1245-1252.
|
| [13] |
姚海元, 房卓, 郝军, 等. 多智能体航道通航标准仿真技术[J]. 水运工程, 2016(5): 116-120. ( YAO Haiyuan, FANG Zhuo, HAO Jun, et al. Simulation method of criteria for waterway navigation based on multi-agent technology[J]. Port and Waterway Engineering, 2016(5): 116-120. DOI:10.3969/j.issn.1002-4972.2016.05.021 (in Chinese)) |
| [14] |
廖鹏. 内河船舶交通流量的时空分布特征[J]. 水利水运工程学报, 2009(2): 33-38. ( LIAO Peng. Temporal and spatial distribution of traffic flow in inland waterways[J]. Hydro-Science and Engineering, 2009(2): 33-38. DOI:10.3969/j.issn.1009-640X.2009.02.006 (in Chinese)) |
| [15] |
LIAO P. Improved analytical model for estimating the capacity of a waterway lock[J]. Journal of Waterway, Port, Coastal and Ocean Engineering, 2018, 144(6): 04018021. DOI:10.1061/(ASCE)WW.1943-5460.0000473 |
| [16] |
BORSHCHEV A. Multi-method modelling: AnyLogic[M]//BRAILSFORD S, CHURILOV L, DANGERFIELD B. Discrete-Event Simulation and System Dynamics for Management Decision Making. West Sussex: John Wiley and Sons Ltd, 2014.
|
| [17] |
LEEMIS L M, MCQUESTON J T. Univariate distribution relationships[J]. American Statistician, 2008, 62(1): 45-53. DOI:10.1198/000313008X270448 |
2. Department of Port, Waterway and Coastal Engineering, School of Transportation, Southeast University, Nanjing 210096, China
 2019
2019 
