2. 南京水利科学研究院,江苏 南京 210029;
3. 河海大学 力学与材料学院,江苏 南京 211100
混凝土作为当前应用最广泛的建筑材料,其力学性能研究对混凝土结构设计与安全防护具有重要意义。由于混凝土抗压和抗拉性能之间的巨大差异,混凝土在结构中往往用于承受压力,导致人们对混凝土力学性能的研究主要侧重于抗压性能方面。相较于混凝土的抗压能力研究,其抗拉能力的研究则起步较晚,发展较缓慢。文献[1-2]仅侧重于研究混凝土的拉伸强度,认为混凝土在达到最大荷载时突然断裂,对混凝土的轴拉破坏过程认识不完整。范向前等[3]分析了7种不同应变速率对混凝土应力-应变关系曲线、轴向拉伸强度、弹性模量、峰值应变的变化规律。张艳红等[4]进行了全级配混凝土轴拉试验,加载方式采用位移控制,获得了应力-应变全曲线。彭刚等[5]进行了不同加载速率的单轴压缩试验,同步采集了声发射数据,构建了基于AE参数的损伤变量模型,并基于该模型进行了动态损伤特性的速率反映。胡伟华等[6]基于声发射研究混凝土材料动态损伤特性及损伤演化规律,进行了3种加载速率下混凝土单轴压缩试验; 研究表明混凝土在不同阶段的损伤程度、破坏形态与加载应变速率有关,加载速率越大,混凝土破坏越严重,损伤路径越短,且损伤发展的起点与终点是重合的。随着研究的深入,学者们开始考虑影响混凝土拉伸性能的多方面因素,如龄期[7]、冻融循环[8]、不同初始损伤[9]等。
综合国内外研究现状发现,关于带裂缝混凝土的轴拉力学性能及声发射特征参数的研究极为匮乏。而实际工程中,混凝土结构大多带缝工作,尤其是大坝结构。因此,本文针对带裂缝混凝土在轴拉荷载作用下的力学性能和声发射特征参数开展研究,可为混凝土结构安全评估提供相关技术参考。
1 试验简介 1.1 试件制备试验采用《水工混凝土试验规程》[10]中的轴向拉伸C型试件。试件具体尺寸如图 1(a)。采用自制夹具,设计带初始缝长为20, 30和40 mm的3种不同尺寸,厚度1 mm的中间贯穿裂缝混凝土试件。预制缝钢板要求如图 1(b)所示。同时浇筑无缝混凝土试件作对比试验,每组各4个试件。试件模具为钢模,采用人工振动棒振捣,室内覆盖透水棉布养护至28 d,自然放置90 d后开始试验。试件制作如图 1(c)。

|
图 1 试件尺寸与制备(单位:mm) Fig.1 Dimension and preparation of specimen (unit: mm) |
所有试件强度等级均为C25,采用南京生产的海螺牌复合硅酸盐水泥P·C 32.5R,粗骨料连续粒级颗粒级配碎石(最大直径d1≤20 mm),细骨料采用天然河砂(最大粒径d2≤5 mm),配合比为水:水泥:砂:石子=0.440:1.000:1.225:2.485,浇筑24 h后拆模。
1.2 试验设备试验机为1 000 kN微机控制电液伺服低周疲劳试验机,压力传感器量程为±30 kN,加载方式为力控,控制应变速率在10-6 /s~10-5 /s。采用美国Epsilon公司生产的引伸计测量无缝混凝土变形,标距250 mm,变形测量范围-2.5~2.5 mm;采用长春机械科学研究院生产的夹式引伸计测量裂缝张口位移,标距为12 mm,测量范围0~2 mm。
2 试验数据取舍规则由于混凝土本身固有的离散性,试验过程中可能出现的操作失误以及高变形速率下试件惯性等诸多问题,所得试验结果必然存在一定的离散性。为保证试验数据的可靠性,每组试件设计4个,测试结果偏离平均值±15%的数据舍掉。对于无裂缝试件、当断裂位置不在直拉段以及有预制缝试件、断裂位置不通过预制缝两种情况,所得试验数据均视为失败舍去。最终保证每组数据不少于3个,少于3个有效数据的小组则试验重做。试件有效断面如图 2。

|
图 2 试件有效断面 Fig.2 Effective section of specimen |
不同初始缝长的混凝土轴拉强度及其均值变化曲线如图 3。由图 3可知,随着初始缝长的增加,混凝土轴拉强度逐渐减小,二者之间近似为线性关系。通过线性回归分析,拟合得到混凝土抗拉强度和初始预制缝宽度的关系式如下:

|
图 3 混凝土轴拉强度与初始裂缝长度关系 Fig.3 Relationships between axial tensile strength and initial crack length of concrete |
| $ {f_{\rm{t}}} = - 0.2{a_0} + 2.1\quad \left( {{R^2} = 0.965\;05} \right) $ | (1) |
式中:ft为混凝土轴向拉伸强度(MPa);a0为初始预制缝长度(mm)。
初始缝长为20,30和40 mm的轴拉强度相对于无缝试件分别降低了25%,34%和42%。这是由于随着裂缝长度的增加,混凝土受力面积逐渐减小,在其受荷载作用发生断裂破坏时,有效承载破坏面逐渐减小,故可承受的最大荷载必然减小。此外,由于预制缝尖端的应力集中效应,混凝土更容易破坏,导致含有预制缝的试件轴拉强度折减幅度较大。
3.2 裂缝对混凝土弹性模量影响对于无缝混凝土试件,弹性模量计算式为:Et=σ0.5/ε0.5,其中:Et为轴心抗拉弹性模量(MPa); σ0.5为50%破坏应力;ε0.5为σ0.5所对应的应变值。抗拉弹性模量取应力从0~0.5ft的割线弹性模量。
对于带裂缝混凝土,计算弹性模量采用Tada应力强度因子手册[10]给出的P-dCMOD(即荷载-张口位移曲线,其中P为试验机所施加的外力荷载;dCMOD为张口位移,即中间预制裂缝受荷载作用上下表面的相对位移)关系:
| $ {d_{{\rm{CMOD}}}} = \frac{{4\sigma a}}{E}{V_1}(a/b) $ | (2) |
| $ {V_1}(a/b) = - 0.071 - 0.535a/b + 0.169{(a/b)^2} + 0.02{(a/b)^3} - 1.071\frac{1}{{a/b}}\ln (1 - a/b) $ | (3) |
式中:V1为几何因子,和裂缝的几何形状、试样形式有关;σ为应力(MPa);a为裂缝长度的1/2(mm);b为试件截面宽度的1/2(mm)。
通过混凝土轴拉试验获得P-dCMOD曲线,在曲线起始线性部分任找3点(P1, dCMOD1),(P2, dCMOD2),(P3, dCMOD3),然后连同初始缝长及试件宽度代入式(3),求得E1,E2,E3,计算其平均值,即求得计算弹性模量E。
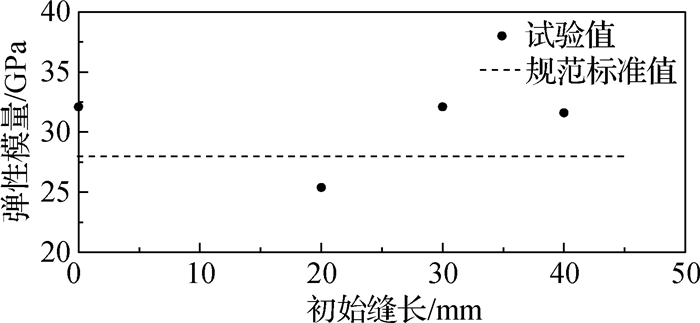
图 4给出弹性模量比均值与初始裂缝长度的关系,其中规范的标准值参考《混凝土结构设计规范》(GB 50010—2010),C25混凝土弹性模量取值28 GPa。由图 4可知,混凝土弹性模量受初始缝长的影响较小,可认为弹性模量保持不变。混凝土弹性模量主要与混凝土本身材料性能,如骨料品质、水灰比、砂率、浇筑质量及养护条件等有关[11]; 还与应变速率有关。随着应变速率的增加,混凝土弹性模量逐渐提高[3]。试验所用试件均同一批浇筑完成,在准静态荷载作用下轴拉破坏,因此弹性模量基本不变。
|
图 4 混凝土弹性模量与初始缝长关系 Fig.4 Relationships between elastic modulus and initial crack length of concrete |
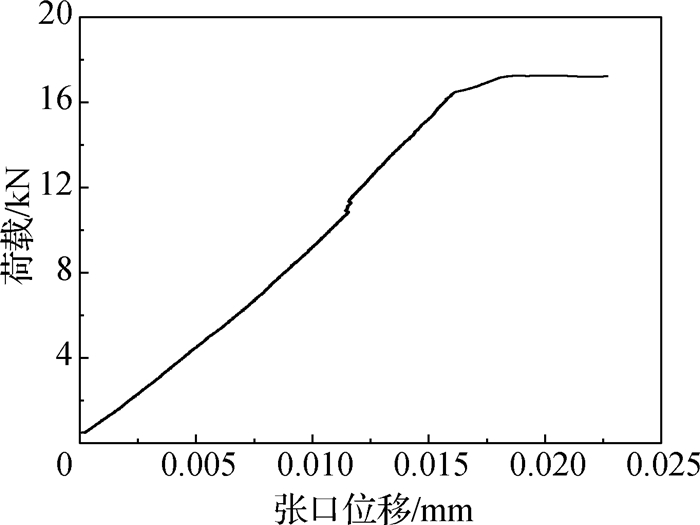
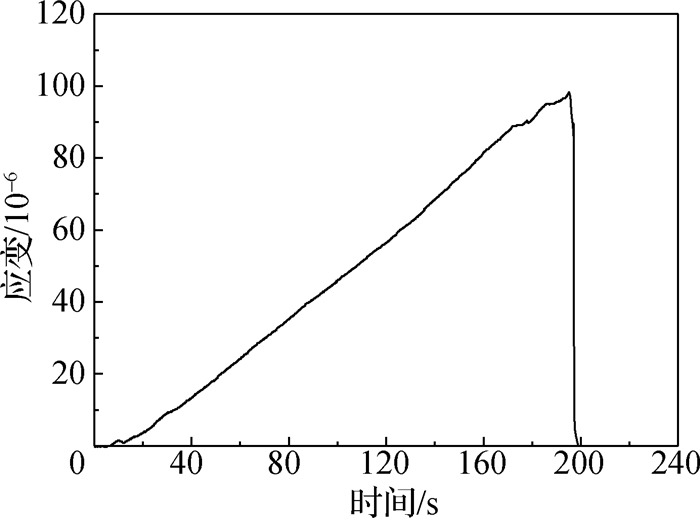
由于试件截面尺寸较小,中间预制缝的存在导致混凝土在承受荷载发生破坏时的断裂过程区较小; 在采用力控加载方式过程中,混凝土试件容易发生突然断裂。图 5为引伸计测得的P-dCMOD曲线图。图 6为试验应变片测得的应变-时间曲线。由图 5和6可知,试件的起裂和失稳几乎同时发生,可认为裂缝一经起裂就迅速失稳破坏。由《应力强度因子手册》[12]得:
|
图 5 P-dCMOD曲线 Fig.5 Curve of P-dCMOD |
|
图 6 应变与时间关系曲线 Fig.6 Relationship curve between strain and time |
| $ {K_{\rm{I}}} = F\sigma \sqrt {{\rm{ \mathsf{ π} }}a} $ | (4) |
| $ F = \frac{{1 - 0.5\frac{a}{b} + 0.326{{\left( {\frac{a}{b}} \right)}^2}}}{{\sqrt {1 - \frac{a}{b}} }} $ | (5) |
式中:KI为应力强度因子(MPa·m1/2);F为几何因子,与裂缝几何形状、试样形式有关。
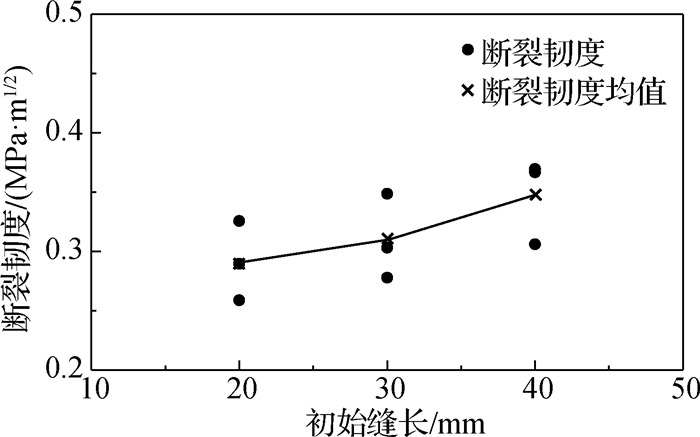
本次试验,上述参数均为已知,计算结果见图 7。由图 7可知,当混凝土初始裂缝长度小于50 mm时,即缝高比(初始裂缝长度与试件宽度的比值)小于0.5时,初始裂缝长度越大,混凝土断裂韧度也越大。
|
图 7 混凝土断裂韧度与初始缝长关系 Fig.7 Relationships between fracture toughness and initial crack length of concrete |
胡晓威[13]完成了缝高比为0.1,0.3和0.5的3组劈拉试验。试验发现,混凝土失稳韧度与初始缝高比之间基本呈线性增长关系(图 8(a))。图 8中横坐标a0代表初始缝高比,纵坐标KICun-exp代表失稳断裂韧度,β为相对受压荷载分布宽度。

|
图 8 文献中有关断裂韧度与缝高比关系曲线 Fig.8 Relationships between fracture toughness and seam high ratio from documents |
Ince[14]开展了中间带缺口的混凝土立方体试件劈裂试验研究,发现当初始缝高比设计值为0.1~0.4时,缝高比越大,起裂韧度越大;此外,Ince认为当缝高比增大到0.5时,起裂韧度有减小的可能(如图 8(b))。图 8中纵坐标KICini代表失稳断裂韧度。
胡少伟等[15]开展了两种强度等级三点弯曲梁试验,分析了缝高比对断裂韧度的影响,发现缝高比越大,起裂韧度和失稳韧度越大(如图 8(c))。
综合本次试验结果和上述引文分析可得:在缝高比较小情况下,混凝土起裂韧度、失稳韧度随裂缝长度的增加均表现出增大趋势,且对于轴拉、弯拉和劈拉等不同形式的试件,此规律一致;当缝高比大于0.5后,断裂韧度有下降可能,作者认为有必要在本次研究基础上,增大缝高比设计,开展更深入的研究。
3.4 声发射凯塞效应(Kaiser)与费利西蒂效应的影响分析当混凝土受外力作用,内部产生的损伤以弹性波形式释放出瞬时应变能的现象称为声发射(AE)。利用声发射现象实时动态地获得材料内部开裂信息和研究其损伤过程是一种有效的方法[16]。Kaiser效应是指材料在受荷过程中声发射活动所具有的不可逆性,材料科学中将Kaiser效应定义为:当材料所受荷载在没有到达其曾经历过的最大荷载水平前几乎不产生声发射, 而一旦超过最大荷载水平时声发射活动便再度出现的现象[17]。因此,研究Kaiser效应可以反映混凝土原先所受损伤或结构缺陷的严重程度,是确定缺陷严重程度的重要评判依据。通过分析混凝土轴拉断裂破坏过程中的Kaiser效应,研究混凝土在变幅循环荷载作用下的损伤发展规律。
3.4.1 声发射设备参数设置声发射设备为SENSOR HIGHWAY Ⅱ型声发射采集系统,参数设置如下:采样频率为1 MHz,阈值为40 dB,前放增益为40 dB,顶触发为256 μs,采样长度为3 KB,带通滤波范围为1~400 kHz。
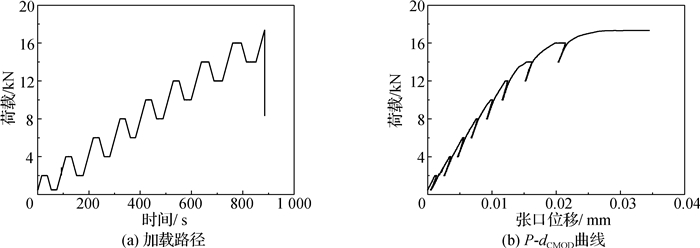
3.4.2 加载方案试验加载采用分级加载方式,加载速率约控制在10-6/s~10-5/ s。加载路径如图 9(a),同步采集的荷载-张口位移曲线如图 9(b)。
|
图 9 试验加载路径和荷载-张口位移曲线 Fig.9 Test loading path and load-displacement curve |
由图 9可见,混凝土加卸载初期,P-dCMOD曲线加卸载曲线性关系较好;随着荷载水平的提高,P-dCMOD曲线加载曲线逐渐进入非线性;说明此时混凝土已经发生较大塑性变形,甚至已经产生裂缝,当变形增大到一定量时,混凝土即发生断裂破坏。
3.4.3 混凝土轴拉声发射Kaiser效应分析图 10为声发射振铃计数和荷载历程关系。可见,对于轴拉强度较高的试件(图 10(a)),在早期低荷载水平作用时,声发射信号出现较少;而对于轴拉强度较低的试件(图 10(b)和(c)),在低荷载水平时有大量声发射信号发生。因此,可通过比较加载初期采集到的声发射信号强弱,来判断试件强度的高低。

|
图 10 不同初始缝长混凝土静态轴拉声发射振铃计数与荷载历程关系 Fig.10 Relationships between ringing counting and load progress of concrete with different initial crack lengths under static axial tension stress |
在再加载未超过加载历史的最大荷载值之前,若没有接收到显著的声发射信号,可认为表现出明显的Kaiser效应。由图 10可知,混凝土出现了明显的Kaiser效应。在每次循环加载过程中,声发射的不可逆程度是不同的,这种不可逆程度可用不可逆比表示,即Felicity比定义为:
| $ \mathit{F}{\mathit{R}_\mathit{i}}{\rm{ = }}{\mathit{F}_{\mathit{i}{\rm{ + 1}}}}{\rm{/}}{\mathit{F}_\mathit{i}} $ | (6) |
式中:Fi为第i次加载到的荷载水平;Fi+1为第i+1次加载过程中出现显著声发射活动时对应的荷载值。
显著声发射信号的定义根据我国航天业标准QJ 2914—1997《复合材料结构件声发射检测方法》[18]提出的确定二次加载声发射起始荷载的判据:①在恒载1 min周期内事件计数不小于5;②在10%的载荷增量中事件计数不小于10。
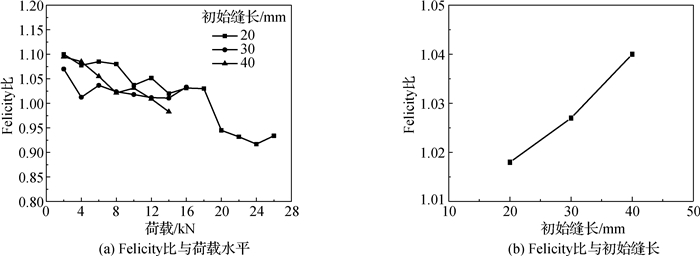
表 1给出了不同初始缝长混凝土在不同加载阶段的Felicity比, 试件C25-20-1, C25-30-1, C25-40-1对应的FRi均值分别为1.018,1.027和1.040。图 11给出了Felicity比与荷载水平和裂缝长度的关系变化曲线。
| 表 1 不同初始缝长混凝土静态轴拉Felicity比 Tab.1 Felicity ratios of concrete with different initial crack lengths under static axial tension |
|
图 11 Felicity比与荷载水平和初始裂缝长的关系 Fig.11 Changes of Felicity ratios along with load level and initial crack length |
由图 11(a)可知,随着荷载水平增加,Felicity比呈下降趋势。这是由于随着荷载水平的提高,混凝土内部损伤程度加剧;下一次循环刚超过或未达到上一次加载荷载最大值时就会产生声发射信号,表明Kaiser效应逐渐减弱。混凝土的声发射Kaiser效应本质上是由混凝土内部损伤决定,而不是由其受荷载历史决定。这一现象与文献[19-20]所述结论基本一致。
由图 11(b)可知,随着初始裂缝长的增大,Felicity比均值逐渐增大。这是由于初始裂缝长度越大,混凝土内部初始损伤程度相对就越严重。下一次加载达到之前的损伤量需要更多时间,导致出现声发射信号的时间将逐渐推迟,Kaiser效应逐渐增强。因此,根据Felicity比的大小,一定程度上可判断混凝土内部初始损伤程度。
4 结语(1) 随着初始裂缝长度的增加,混凝土弹性模量保持常量,混凝土轴拉强度表现出线性下降的规律,以无缝混凝土试件为基准,初始裂缝长度为20, 30和40 mm试件的轴拉强度分别降低了25%,34%和42%。
(2) 在轴拉力控加载方式下,混凝土起裂时刻与失稳时刻基本同时发生,当缝高比小于0.4时,其断裂韧度随缝高比的增加逐渐增大,且对于轴拉、弯拉和劈拉3种不同形式的试件,此规律一致。
(3) 轴拉循环荷载作用下,混凝土表现出明显的Kaiser效应。根据混凝土在受荷初期声发射信号的强弱可以判断混凝土强度的高低,且声发射Kaiser效应本质上是由混凝土内部损伤程度决定。
| [1] |
MALVAR L J, ROSS C A. A review of strain rate effects for concrete in tension[J]. ACI Materials Journal, 1998, 95(6): 735-739. |
| [2] |
ROSS C A. Effects of strain rate on concrete strength[J]. ACI Material Journal, 1995, 92(1): 37-47. |
| [3] |
范向前, 胡少伟, 陆俊, 等. 混凝土静动态轴向拉伸力学性能[J]. 硅酸盐学报, 2014, 42(11): 1349-1354. ( FAN Xiangqian, HU Shaowei, LU Jun, et al. Static and dynamic axial tension properties of concrete[J]. Journal of the Chinese Ceramic Society, 2014, 42(11): 1349-1354. (in Chinese)) |
| [4] |
张艳红, 胡晓, 杨陈. 全级配混凝土轴拉应力-变形全曲线试验研究[J]. 中国水利水电科学研究院学报, 2017, 15(2): 96-100. ( ZHANG Yanhong, HU Xiao, YANG Chen. The study on the tensile stress-deformation curve of fully-graded concrete[J]. Journal of China Institute of Water Resources and Hydropower Research, 2017, 15(2): 96-100. (in Chinese)) |
| [5] |
彭刚, 王乾峰, 陈灯红, 等. 基于声发射参数的混凝土循环加卸载动态损伤破坏特性研究[J]. 三峡大学学报(自然科学版), 2015, 37(6): 1-9. ( PENG Gang, WANG Qianfeng, CHEN Denghong, et al. AE-based dynamic damage failure characteristic of concrete under cyclic loading and unloading conditions[J]. Journal of China Three Gorges University (Natural Sciences), 2015, 37(6): 1-9. (in Chinese)) |
| [6] |
胡伟华, 彭刚, 黄仕超, 等. 基于声发射技术的混凝土动态损伤特性研究[J]. 长江科学院院报, 2015, 32(2): 123-127, 132. ( HU Weihua, PENG Gang, HUANG Shichao, et al. Dynamic damage features of concrete based on acoustic emission technology[J]. Journal of Yangtze River Scientific Research Institute, 2015, 32(2): 123-127, 132. (in Chinese)) |
| [7] |
SHEN D, JIANG J, WANG W, et al. Tensile creep and cracking resistance of concrete with different water-to-cement ratios at early age[J]. Construction and Building Materials, 2017, 146: 410-418. DOI:10.1016/j.conbuildmat.2017.04.056 |
| [8] |
胡少伟, 王阳. 不同冻融方式下混凝土双K断裂韧度对比试验[J]. 水利水运工程学报, 2018(2): 91-97. ( HU Shaowei, WANG Yang. Experimental study on double-K fracture toughness of concrete in different freezing and thawing modes[J]. Hydro-Science and Engineering, 2018(2): 91-97. (in Chinese)) |
| [9] |
范向前, 胡少伟, 陆俊, 等. 不同初始损伤混凝土动态轴向拉伸试验研究[J]. 振动与冲击, 2016, 35(17): 117-120. ( FAN Xiangqian, HU Shaowei, LU Jun, et al. Dynamic axial tension tests of concrete with different initial damages[J]. Journal of Vibration and Shock, 2016, 35(17): 117-120. (in Chinese)) |
| [10] |
TADA H, PARIS P C, IRWIN G R. The stress analysis of cracks handbook[M]. New York: ASME Press, 2000.
|
| [11] |
曹茂柏. 对混凝土弹性模量影响因素的探讨[J]. 科技通报, 2012, 28(12): 195-197. ( CAO Maobo. The discussion of the influence of the mix proportion of concrete with concrete elastic modulus[J]. Bulletin of Science and Technology, 2012, 28(12): 195-197. DOI:10.3969/j.issn.1001-7119.2012.12.066 (in Chinese)) |
| [12] |
中国航空研究院. 应力强度因子手册[M]. 北京: 科学出版社, 1993. ( Chinese Aeronautical Establishment. Handbook of stress intensity factors[M]. Beijing: Science Press, 1993. (in Chinese))
|
| [13] |
胡晓威.中央带缺口立方体试件的双K断裂韧度及其率相关性分析[D].大连: 大连理工大学, 2013. (HU Xiaowei. Using central-notched splitting-tension cube specimens to study double-K fracture toughness parameters and their rate dependence[D]. Dalian: Dalian University of Technology, 2013. (in Chinese)) http://cdmd.cnki.com.cn/Article/CDMD-10141-1013198785.htm
|
| [14] |
INCE R. Determination of concrete fracture parameters based on peak-load method with diagonal split-tension cubes[J]. Engineering Fracture Mechanics, 2012, 82(3): 100-114. |
| [15] |
胡少伟, 范向前, 陆俊. 缝高比对不同强度等级混凝土断裂特性的影响[J]. 防灾减灾工程学报, 2013, 33(2): 162-168. ( HU Shaowei, FAN Xiangqian, LU Jun. Influence of crack-depth ratio on fracture features of different strength grade of concrete[J]. Journal of Disaster Prevention and Mitigation Engineering, 2013, 33(2): 162-168. (in Chinese)) |
| [16] |
GROSSE C U, FINCK F. Quantitative evaluation of fracture processes in concrete using signal-based acoustic emission techniques[J]. Cement and Concrete Composites, 2006, 28(4): 330-336. DOI:10.1016/j.cemconcomp.2006.02.006 |
| [17] |
孙吉主, 周健, 唐春安. 影响岩石声发射的几个因素[J]. 地壳形变与地震, 1997, 17(2): 1-5. ( SUN Jizhu, ZHOU Jian, TANG Chun'an. Factors affecting acoustic emission of rock[J]. Crustal Deformation and Earthquake, 1997, 17(2): 1-5. (in Chinese)) |
| [18] |
QJ 2194—1997复合材料结构件声发射检测方法[S]. (QJ 2194—1997 Acoustic emission detection method for composite structure parts[S]. (in Chinese))
|
| [19] |
王岩, 王瑶, 路桂娟, 等. 变幅循环荷载下混凝土轴拉声发射特性试验[J]. 河海大学学报(自然科学版), 2014, 42(1): 45-49. ( WANG Yan, WANG Yao, LU Guijuan, et al. Experimental study on acoustic emission characteristics of concrete under variable amplitude cyclic tension loading[J]. Journal of Hohai University (Nature Sciences), 2014, 42(1): 45-49. DOI:10.3876/j.issn.1000-1980.2014.01.009 (in Chinese)) |
| [20] |
吴胜兴, 张顺祥, 沈德建. 混凝土轴心受拉声发射Kaiser效应试验研究[J]. 土木工程学报, 2008, 41(4): 31-39. ( WU Shengxing, ZHANG Shunxiang, SHEN Dejian. An experiment study on Kasier effect of acoustic emission in concrete under uniaxial tension loading[J]. China Civil Engineering Journal, 2008, 41(4): 31-39. DOI:10.3321/j.issn:1000-131X.2008.04.005 (in Chinese)) |
2. Nanjing Hydraulic Research Institute, Nanjing 210029, China;
3. College of Mechanics and Materials, Hohai University, Nanjing 211100, China
 2019
2019 
