2. 天津城建大学 土木工程学院,天津 300384;
3. 交通运输部天津水运工程科学研究所,天津 300456
截至2015年底,我国沿海港口拥有生产性泊位超过7 000多个。码头供船舶停靠,是水运与公路和铁路网中的枢纽工程,其安全状态直接影响到整个运输网络的运营效率和安全。在船舶停靠过程中,船舶失控撞击码头事件频繁发生,撞击后码头结构发生损伤破坏导致其功能失效影响生产运输,从而产生巨大的经济损失。
在国内,高桩码头是应用广泛的码头结构型式,基桩作为高桩码头唯一的抗侧力构件,在船舶偶然撞击作用下往往发生不同程度的破坏。然而,由于基桩位于水中,发生船撞事故后采用现有检测技术很难检测到其损伤破坏的程度,这对事故后期高桩码头的评估和修复工作带来严峻挑战。
近年来,随着计算机仿真技术的飞速发展,国内外学者研究应用有限元法进行船与结构碰撞过程的数值模拟分析。Yuan等[1]研究了单艘驳船和驳船队撞击方形、圆形桥墩的撞击力和船艏撞深,并讨论了船舶速度对撞击的影响,被撞桥墩混凝土采用刚性模型。Manuel等[2]利用数值方法模拟了单墩在驳船撞击作用下的撞击力和应力分布,并讨论了船舶撞击速度和桥墩有限元网格划分密度对撞击力时程的影响。王君杰等[3]提出两种可用于船桥碰撞动力分析和进行船-桥碰撞动力设计的简化力学模型,通过不同吨位船舶以不同速度与刚性墙进行碰撞分析,标定所提出模型的参数。欧碧峰[4]根据4艘船舶的数值模拟计算结果,以受撞刚体为基准,给出了3种简化的动力曲线。现有的成果主要以受撞体为刚体或弹性体为基准,然而为了能够评估船撞码头事故后结构的性能状态,数值仿真分析需考虑结构的材料非线性和几何非线性。同时,在船撞结构数值仿真分析中需已知结构所受的撞击力和撞击时间,但实际船撞事故中很难获得这两个变量。
为解决上述问题,本文提出以动量守恒定律为基础,试算输入不同简化撞击力-时间荷载曲线,计算结构的动力响应与现场检测结果一致为准则,基于有限元模型分析船撞结构损伤破坏的数值分析方法。以船撞中泉石化系缆墩事故为背景,建立系缆墩的有限元模型,对其船撞事故进行模拟,分析结构的损伤破坏情况。
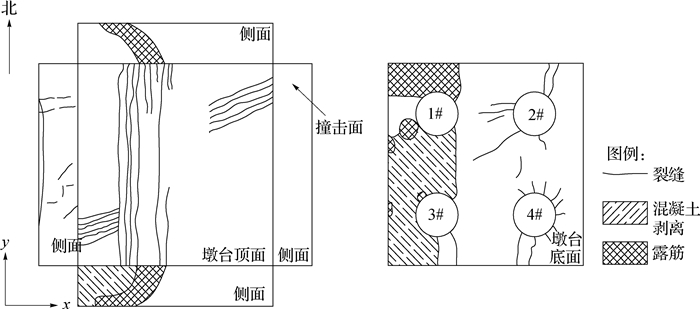
1 船撞系缆墩事故背景2017年5月马绍尔群岛籍“CTI CONDOTTI”号出口汽油船(6.6万t)在靠泊于泉州中泉石化码头作业区过程中由于船员操作失误,船舶以0.86 m/s的船速撞击在系缆墩墩台侧面上,撞击面积约为2.5 m×2.3 m(见图 1);船舶撞击作用导致系缆墩台发生剪切破坏,墩台底部混凝土大面积开裂(见图 1)。对受损高桩墩进行现场检测,并绘制墩台破坏示意图(见图 2)。通过现场检测可知,墩台的x向残余位移为657 mm,y向残余位移为30 mm。经检测,泥面以上部分混凝土灌注桩钢套筒未发生明显的屈服现象,但由于现有检测技术手段限制,无法检测到灌注桩钢套筒内部的混凝土和土层以下钢套筒的损伤破坏情况。

|
图 1 墩台撞击照片 Fig.1 Impact surface of abutment |
|
图 2 墩台破坏示意 Fig.2 Schematic diagram of damaged cleat |
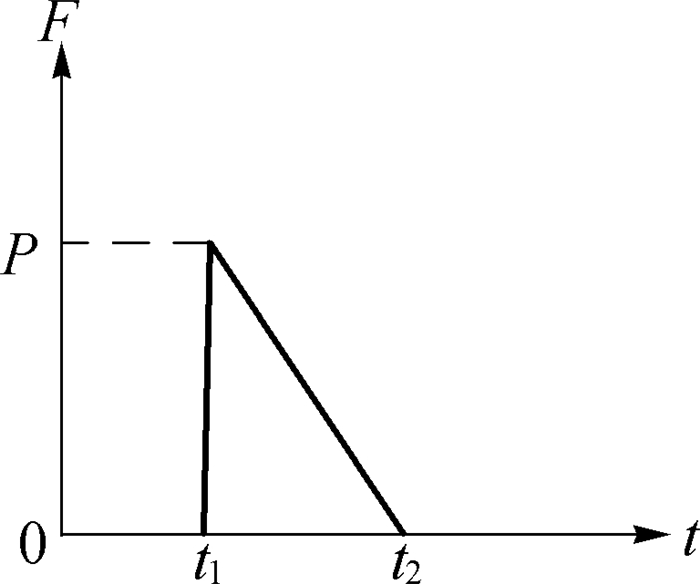
船舶撞击结构涉及能量转移、消散等复杂过程,导致真实模拟船撞码头过程相当困难。为了简化船撞结构过程,可在有限元结构模型中输入撞击力-时间荷载曲线进行简化计算模拟结构的动力响应。然而,实际工况中船撞结构属于偶然事故,无法直接获得撞击过程中的撞击力-时间荷载曲线,可通过撞击过程中的动量守恒求解撞击力-时间荷载曲线。根据文献[5]给出的船舶撞击结构的三角形荷载简化模型,如图 3所示。船舶撞击力产生的冲量I的表达式为:
| $ I=\frac{1}{2} P\left(t_{2}-t_{1}\right)=\frac{1}{2} P T $ | (1) |
|
图 3 撞击力简化模型 Fig.3 Simplified model of impact force |
式中:P为最大撞击力;t1为撞击开始时刻;t2为撞击结束时刻;T为撞击持续时间。
船舶撞击结构过程满足动量守恒定律,即撞击力产生的冲量与船舶动量相等,可得:
| $ I=M\left(V-V_{0}\right)=M V $ | (2) |
式中:I为船舶撞击力产生的冲量;M为船舶质量;V为船舶发生碰撞前的速度;V0为船舶碰撞结束后的速度,取0。
根据式(1)和(2)可得:
| $ P=2 M V / T $ | (3) |
船撞事故发生时船舶质量和船舶速度可通过船上固有设备获得,由此可确定式(3)中的2MV为固定值,但由于撞击持续时间T未知,无法获得撞击力-时间荷载曲线,因此先假定时间T1后根据式(3)计算获得撞击力-时间荷载曲线,输入至有限元模型中进行计算,计算完成后提取墩台位移时程曲线,获得墩台残余位移与撞击事故发生后结构的实际残余位移进行比对。若比对结果一致则认定数值仿真结果与实际情况一致,再分析结构的动力响应和破坏模式。若不一致,重复上述步骤假定撞击持续时间T2,T3,…,Tn,根据式(3)计算获得撞击力-时间荷载曲线,输入至有限元程序进行计算,直至数值仿真结果与实际情况一致时停止计算。
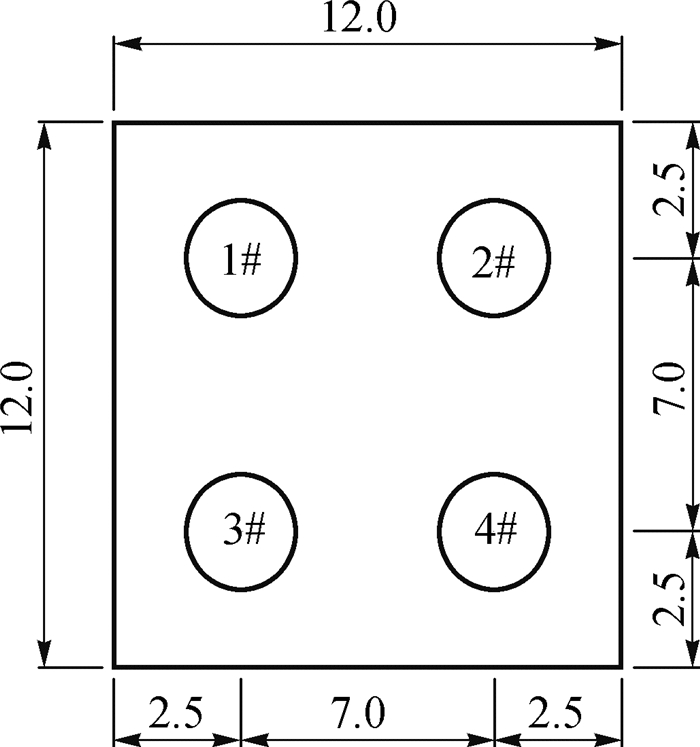
3 有限元模型的建立 3.1 结构模型系缆墩由墩台和4根带有钢套筒的钢筋混凝土灌注桩组成,灌注桩打入基岩,灌注桩顶部伸入墩台中通过现浇混凝土固结为整体。墩台的长宽高为12.0 m×12.0 m×2.5 m,采用C40混凝土,钢筋采用HRB400,钢筋体积配筋率为0.30%;钢筋混凝土灌注桩直径为2.6 m,桩顶到基岩顶部长37.0 m,桩位布置如图 4所示。灌注桩的钢套筒采用Q345钢,壁厚为20 mm,混凝土采用C30,钢筋采用HRB400,钢筋体积配筋率为0.98%。根据地质资料显示,从泥面到基岩土层主要分两层,其土层参数如表 1所示。
|
图 4 桩位布置(单位:m) Fig.4 Arrangement plan of pile (unit: m) |
| 表 1 土层参数 Tab.1 Soil parameters |
采用通用有限元动力分析软件LS-DYNA建立系缆墩分离式有限元模型,如图 5(a)所示。混凝土采用常应力实体单元,钢筋采用杆单元,钢套筒采用壳单元,钢筋、混凝土和钢套筒之间采用共节点的方式模拟,土体采用实体单元模拟,其系缆墩和土体模型如图 5(b)所示。

|
图 5 系缆墩有限元模型 Fig.5 FE model of cleat and soil |
系缆墩模型中混凝土材料采用K&C模型进行模拟,其在LS-DYNA中可通过定义MAT_CONCRETE_DAMAGE_REL3实现,该模型仅需定义混凝土密度和抗压强度即可模拟混凝土的力学性能[6]。钢筋采用LS-DYNA中MAT_PLASTIC_KINEMATIC模型,可模拟钢筋从弹性到塑性强化过程。土体采用LS-DYNA中MAT_MOHR_COULOMB模型,可模拟土体在荷载作用下的非线性力学行为。模型参数见表 2。
| 表 2 材料参数 Tab.2 Material parameters |
结构在冲击荷载作用下的应变率效应对结构的动力响应具有显著的影响[7],本文采用的混凝土和钢筋材料均考虑材料的应变率效应,材料的应变率效应一般通过动力增强系数RDIF来考虑。
混凝土强度的RDIF采用K & C模型,其抗拉强度TDIF定义[8]为
| $ T_{\mathrm{DIF}}=f_{\mathrm{td}} / f_{\mathrm{ts}}=\left(\dot{\varepsilon}_{\mathrm{d}} / \dot{\varepsilon}_{\mathrm{ts}}\right)^{\delta}, \dot{\varepsilon}_{\mathrm{d}} \leqslant 1\ \mathrm{s}^{-1} $ | (4) |
| $ T_{\mathrm{DIF}}=f_{\mathrm{td}} / f_{\mathrm{ts}}=\beta\left(\dot{\varepsilon}_{\mathrm{d}} / \dot{\varepsilon}_{\mathrm{ts}}\right)^{\frac{1}{3}}, \dot{\varepsilon}_{\mathrm{d}}>1\ \mathrm{s}^{-1} $ | (5) |
式中:ftd为应变率为
混凝土抗压强度的CDIF定义[8]为:
| $ C_{\mathrm{DHF}}=f_{\mathrm{cd}} / f_{\mathrm{cs}}=\left(\dot{\varepsilon}_{\mathrm{d}} / \dot{\varepsilon}_{\mathrm{cs}}\right)^{1.056 \alpha}, \dot{\varepsilon}_{\mathrm{d}} \leqslant 30\ \mathrm{s}^{-1} $ | (6) |
| $ C_{\mathrm{DIF}}=f_{\mathrm{cd}} / f_{\mathrm{cs}}=\gamma\left(\dot{\varepsilon}_{\mathrm{d}}\right)^{\frac{1}{3}}, \dot{\varepsilon}_{\mathrm{d}}>30\ \mathrm{s}^{-1} $ | (7) |
式中:fcd为应变率为
钢筋强度的FDIF定义[8]为:
| $ F_{\mathrm{DIF}}=\left(\dot{\varepsilon} / 10^{-4}\right)^{\alpha} $ | (8) |
| $ \alpha=0.074-0.040 f_{\mathrm{y}} / 414 $ | (9) |
式中:fy为钢筋的屈服强度(MPa)。
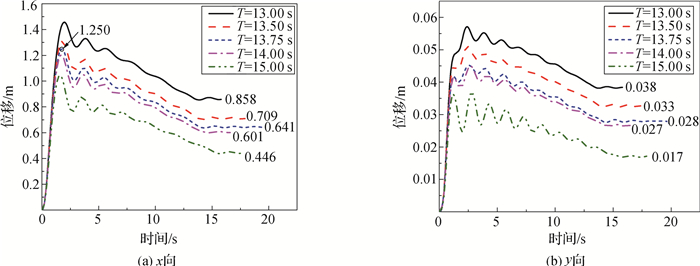
4 数值模拟分析采用逐步逼近法试算了不同撞击时间(T=15.00,13.00,14.00,13.50和13.75 s)对应的最大撞击力(为7.568,8.732,8.109,8.409和8.256 MN)作用下的系缆墩动力响应。图 6给出了不同撞击时间下的系缆墩墩台的位移时程曲线。从图 6可以看出,不同撞击时间T=15.00,13.00,14.00,13.50和13.75 s计算得到的墩台x向残余位移分别为0.466,0.858,0.601,0.709和0.641 m,墩台y向残余位移分别为0.017,0.038,0.027,0.033和0.028 m,现场检测得到的墩台x向残余位移为0.657 m,y向残余位移为0.030 m。当T=13.75 s时,计算得到的墩台残余位移与现场实测相比,x向误差为2.4%,y向误差为7%,因此可以认为当撞击时间为13.75 s,最大撞击力为8.256 MN时,数值模拟的船撞系缆墩的撞击过程与实际过程相近。
|
图 6 不同撞击时间下的墩台位移时程曲线 Fig.6 History curve of abutment displacements with various impact time |
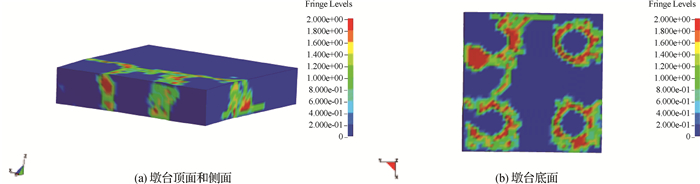
提取数值模拟结果,图 7给出了墩台的混凝土损伤云图。从图 7(a)可以看出,墩台发生剪切破坏,墩台侧面发生不同程度损伤;从图 7(b)可以看出墩台底部在4根灌注桩附近的混凝土发生不同程度的损伤破坏,其破损现象与现场检测情况相符,因此进一步说明数值模拟结果与实际情况相吻合。
|
图 7 墩台的混凝土损伤云图 Fig.7 Damage of abutment |
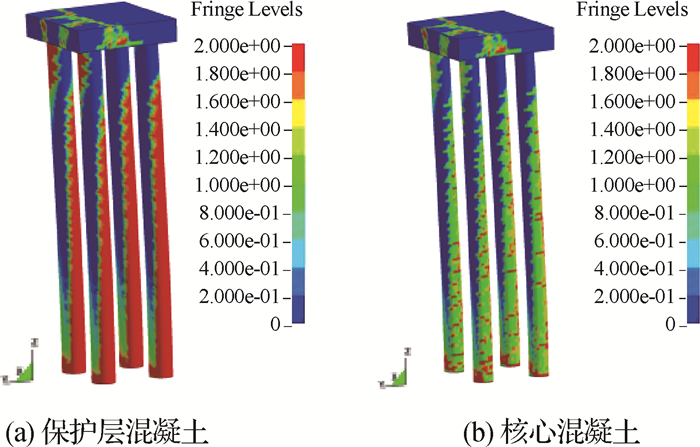
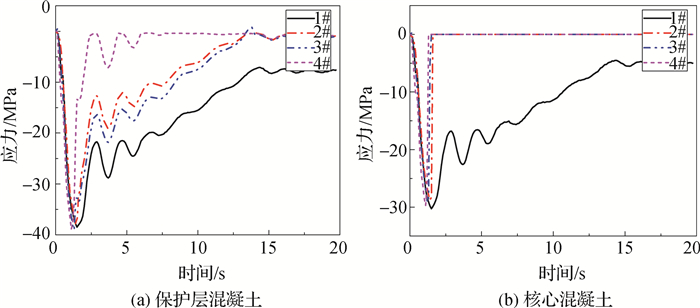
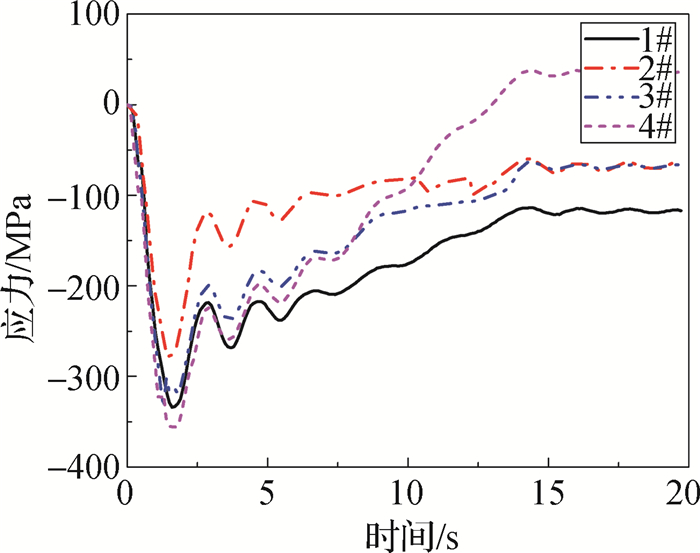
进一步分析桩基在隐蔽部位的损伤破坏情况,图 8给出了灌注桩的混凝土损伤破坏云图。从图 8(a)中可见,4根灌注桩保护层混凝土在撞击侧发生明显的损伤;1#和4#基桩在桩顶部背离撞击侧发生明显损伤破坏,这是由于墩台约束所致;同时可以看出4根基桩在嵌岩端上部的保护层混凝土周圈均发生严重破坏。从图 8(b)可以看出,4根基桩核心混凝土也发生了不同程度的破损,但较保护层混凝土损伤程度轻。图 9给出了背离撞击侧灌注桩嵌岩端上部混凝土应力时程曲线。从图 9(a)可以看出,4根灌注桩底部保护层混凝土在船撞过程中最大应力达38.9 MPa,达到混凝土抗压强度。从图 9(b)可以看出,4根灌注桩底部核心混凝土在船撞过程中最大应力达31.3 MPa,核心混凝土较保护层混凝土应力小。图 10给出了背离撞击侧灌注桩嵌岩端上部钢筋应力时程曲线。从图 10可以看出,4根灌注桩底部钢筋最大应力352.7 MPa,未达到钢筋屈服应力400 MPa,钢筋未发生屈服现象。
|
图 8 灌注桩的混凝土损伤云图 Fig.8 Damage of concrete of filling piles |
|
图 9 灌注桩的混凝土应力时程曲线 Fig.9 Stress history curve of concrete of filling piles |
|
图 10 灌注桩的钢筋应力时程曲线 Fig.10 Stress history curve of steel bar of filling piles |
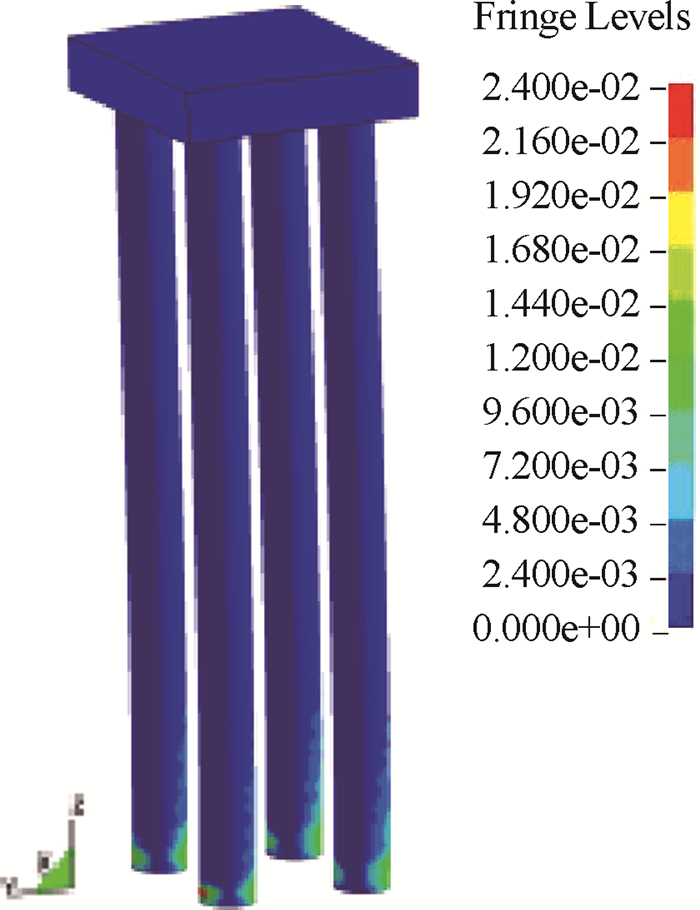
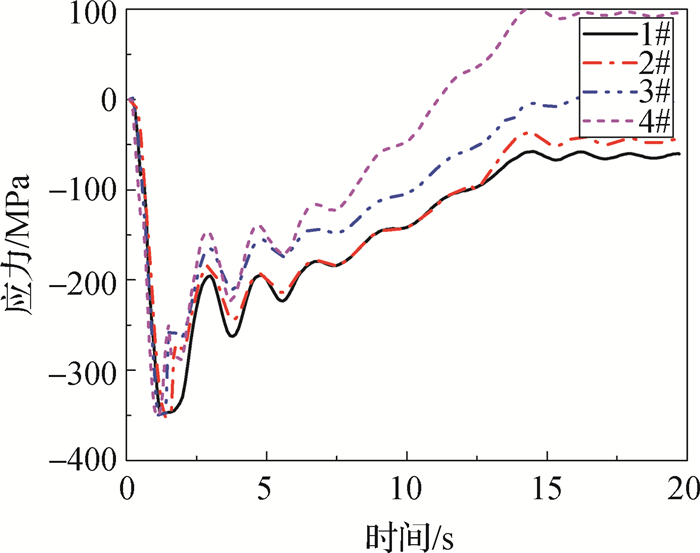
图 11给出了4根灌注桩的钢套筒塑性应变云图,可见4根灌注桩的钢套筒底部在嵌岩端上部发生屈服,最大塑性应变为0.024。同时图 12给出了4根灌注桩的钢套筒应力时程曲线,可以看出4根灌注桩钢套筒底部钢筋在船撞过程中最大应力达352.3 MPa,大于钢套筒屈服应力345 MPa,因此钢套筒在嵌岩端部发生屈服。
|
图 11 灌注桩钢套筒塑性应变云图 Fig.11 Plastic strain of steel sleeve of filling piles |
|
图 12 灌注桩钢套筒应力时程曲线 Fig.12 Stress history curve of steel sleeves of filling piles |
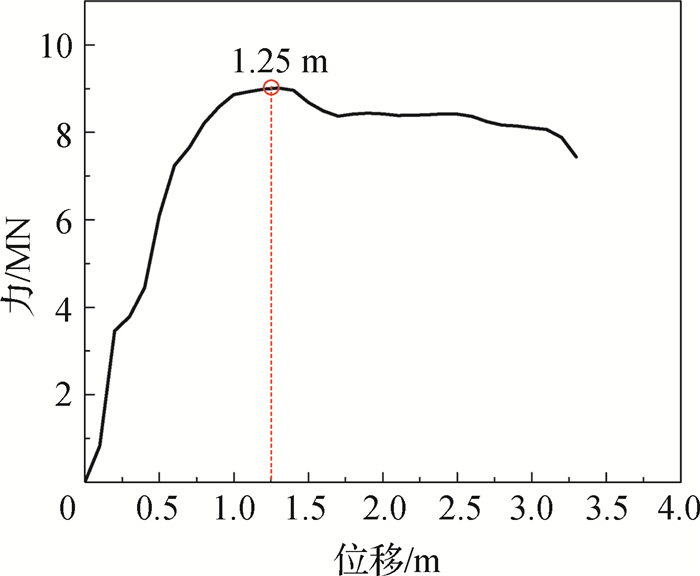
上述从材料层面分析了船舶撞击荷载作用下系缆墩的损伤破损情况,从上述分析可知系缆墩的混凝土灌注桩发生了不同程度的破损,灌注桩内钢筋未发生屈服,钢套筒在嵌岩端上部发生屈服。然而,为了更好服务工程实际,需从结构层面分析系缆墩的力学性能。在墩台撞击的侧面施加x方向水平荷载,计算系缆墩的荷载-位移关系曲线,然后根据系缆墩在船舶撞击过程中所达到的最大位移评估受撞结构的力学性能状态。图 13给出系缆墩的荷载-位移关系曲线。从图中可见,系缆墩的屈服位移为0.6 m,极限位移为3.1 m。
|
图 13 系缆墩的F-S曲线 Fig.13 F-S curve of cleat |
文献[9]对柔性结构定义了延性损伤指数:
| $ D=\frac{d_{\mathrm{p}}-d_{\mathrm{py}}}{d_{\mathrm{pu}}-d_{\mathrm{py}}} $ | (10) |
式中:dp为荷载作用下的最大位移;dpy和dpu分别为单调荷载作用下的屈服位移和极限位移。文献[10]根据延性损伤指数定义了结构的损伤等级,各等级所对应的延性损伤指数分别为:轻微破坏,D=0~0.20;中等破坏,D=0.20~0.55;严重破坏,D=0.55~1.00;完全破坏,D≥1.00。根据图 13可知,系缆墩在船撞过程中x向的最大位移为1.25 m,根据式(10)计算其延性损伤指数为0.26,属于中等破坏范围,因此在工程中需对系缆墩的基桩进行加固处理。
5 结语本文提出了以动量守恒定律为基础,试算输入不同简化撞击力-时间荷载曲线,计算结构的动力响应与现场检测结果一致为准则,基于有限元模型分析船撞结构损伤破坏的数值分析方法。采用该方法对中泉石化船撞高桩系缆墩事故进行了分析计算,结果表明,通过数值计算可以观测到系缆墩隐蔽部位基桩的损伤破坏情况,在灌注桩嵌岩端上部的混凝土发生了不同程度的破损,钢套筒进入了屈服阶段,系缆墩结构整体属于中等破坏程度。因此,所提出的船撞高桩系缆墩简化分析方法可预测基桩隐蔽部位的破损情况和评估结构的整体性能状态,可为后续的修复工程提供参考。
| [1] |
YUAN P, HARIK I E, DAVIDSON M T. Multi-barge flotilla impact forces on bridges[J]. Collisions, 2008. |
| [2] |
MANUEL L, KALLIVOKAS L F, WILLIAMSON E B, et al. A probabilistic analysis of the frequency of bridge collapses due to vessel impact[J]. Bridge Design, 2006. |
| [3] |
王君杰, 卜令涛, 孟德巍. 船桥碰撞简化动力分析方法:简化动力模型[J]. 计算机辅助工程, 2011, 20(1): 70-75. ( WANG Junjie, BU Lingtao, MENG Dewei. Simplified dynamic analysis method of ship-bridge collision: simplified models[J]. Computer Aided Engineering, 2011, 20(1): 70-75. DOI:10.3969/j.issn.1006-0871.2011.01.016 (in Chinese)) |
| [4] |
欧碧峰.基于微平面模型的桥梁船撞数值模拟与简化动力分析[D].上海: 同济大学, 2008. (OU Bifeng. The ship-pounding numerical simulation and simplified dynamic analysis of bridges based on the micro-plane model[D]. Shanghai: Tongji University, 2008. (in Chinese)) http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1416659
|
| [5] |
SHA Y, HAO H. Laboratory tests and numerical simulations of barge impact on circular reinforced concrete piers[J]. Engineering Structures, 2013, 46(1): 593-605. |
| [6] |
LS-DYNA. LS-DYNA user manual[M]. Livermore Software Technology Corporation, 2007.
|
| [7] |
田力, 黄飞. 考虑流体效应的船-桥碰撞数值模拟法研究[J]. 工程力学, 2015, 32(8): 120-128. ( TIAN Li, HUANG Fei. Numerical simulation method for ship-bridge collision considering fluid effect[J]. Engineering Mechanics, 2015, 32(8): 120-128. (in Chinese)) |
| [8] |
陈宇, 孙熙平, 李越松. 施工期台风浪作用下沉箱碰撞破坏分析[J]. 水利水运工程学报, 2018(4): 112-118. ( CHEN Yu, SUN Xiping, LI Yuesong. Pounding damage analysis of caissons during construction under action of storm wave[J]. Hydro-Science and Engineering, 2018(4): 112-118. (in Chinese)) |
| [9] |
SHARIFI A, BANAN M R, BANAN M R. A strain-consistent approach for determination of bounds of ductility damage index for different performance levels for seismic design of RC frame members[J]. Engineering Structures, 2012, 37(4): 143-151. |
| [10] |
LI Z X, CHEN Y, SHI Y D. Seismic damage control of nonlinear continuous reinforced concrete bridges under extreme earthquakes using MR dampers[J]. Soil Dynamics and Earthquake Engineering, 2016, 88: 386-398. DOI:10.1016/j.soildyn.2016.07.015 |
2. School of Civil Engineering, Tianjin Chengjian University, Tianjin 300384, China;
3. Tianjin Research Institute for Water Transport Engineering, MOT, Tianjin 300456, China
 2019
2019 
