2. 陕西省江河水库管理局,陕西 西安 710018
河川径流是一种重要的水资源,径流的科学调节和有效控制,直接关系到流域内工农业生产和社会经济的发展。受全球气候变化和人类活动的双重影响,全球和局部降雨量呈现较大的变异性,极端降水发生频率增加,径流量则呈现更大的时空变异特征。渭河是黄河的第一大支流,在陕西尤其是关中地区社会经济发展中具有重要的意义。国家“一带一路”倡仪的推进和西安市国家中心城市的建设,对渭河流域水资源利用提出更高的要求。自20世纪80年代以来,渭河流域实测径流量总体呈下降趋势,与此同时,社会经济发展对水资源的需求量却日益增加,进一步加剧渭河流域水资源的供需矛盾。变化环境下渭河流域径流变化特征受到流域管理局和国内外专家学者广泛关注,已成为诸多专家学者研究的热点问题[1-3]。
分形理论主要用来描述流域径流序列的复杂性,R/S分析法主要用于对时间序列的持续性和长程记忆性进行分析,并对其未来发展趋势进行预估。近年来分形理论和R/S分析方法在水文学领域广泛应用[4-9],潘国营等[10]采用R/S和Morlet小波分析丹河径流变化特征;冯小庆等[11]对渭河流域径流过程分形特征进行了研究;马宗伟等[12]分析了赣江流域中上游水系分形特征对径流特性的影响;李建林等[13]将R/S分析与灰色系统理论相结合,提出了R/S灰色预测模型以预报黑河出山径流量。采用分形理论和R/S分析方法研究月径流量分形特性及其可持续性,揭示1956—2015年期间渭河流域径流量变化特征及其未来趋势变化,为渭河流域水量调度和水资源严格管理提供科学支撑,具有重要的研究意义。
本文采用Mann-Kendall非参数检验方法[14-15]分析渭河干流各站点的月径流量变化趋势,采用分维数对月径流过程的复杂程度进行定量描述,采用R/S分析法对月径流量时间序列的长程记忆性进行分析,揭示各站点未来月径流量变化趋势,在此基础上研究分维数与Hurst指数两者之间的关系,从历史演变特征和未来发展趋势揭示渭河干流径流量变化特征。
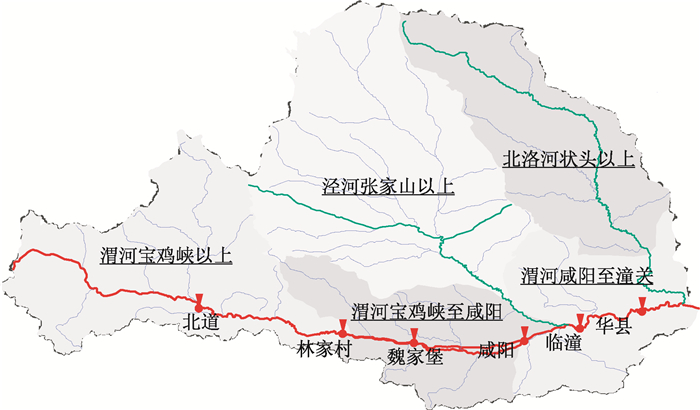
1 资料与方法 1.1 研究区域概况渭河流域地处我国西北干旱半干旱区,为黄河第一大支流,位于东经106°18′~110°37′,北纬33°42′~37°20′之间。北部为黄土高原,南部为秦岭山区。流域总面积134 934 km2,涉及甘肃省的定西市、平凉市、庆阳市、天水市,宁夏回族自治区的固原市,陕西省的宝鸡市、咸阳市、渭南市及西安市的杨凌区共3省(区)10个地区84个县(市、区)。渭河干流全长818 km,渭河按河流形态可分为3段,宝鸡峡大坝以上为上游,河长430 km,河道狭窄;宝鸡峡至咸阳铁路桥段为中游,河长180 km,河道较宽;咸阳至入黄口为下游,河长208 km,比降较小,水流较缓。渭河流域及典型水文站地理位置如图 1所示。
|
图 1 渭河流域及典型水文站分布 Fig. 1 Weihe River basin(WRB) and typicalhydrological stations |
径流数据来源于中华人民共和国水文年鉴黄河流域水文资料、陕西省江河水库管理局统计资料及历年陕西省水资源公报等资料。所采用的测站径流数据经过三性审查,具有良好的周期性、代表性和一致性,可用于相应的计算分析和变化特征研究。
选取渭河干流上北道、林家村、魏家堡、咸阳、临潼和华县6个典型水文站1956—2015年径流量数据进行分析。考虑到部分水文站存在数据缺失情况,采用相关分析法(相关系数大于0.95)、面积比和径流深修正法对魏家堡站和临潼站的缺失数据进行插补。由于径流量反映的是流域径流总量水平而非平均水平,且各站点控制流域面积大小不一,径流量存在较大差异,因此,为了使计算结果具有可比性,利用各站点的实测逐月径流量和流域面积求得各站点的逐月径流深序列,采用月径流深序列计算得到Hurst指数。
1.3 研究方法 1.3.1 分维数计算方法采用Hawth分析工具计算相应测站的分形维数,Hawth分析工具是ArcGIS的扩展工具箱[11]。分维数D的计算式为:
| $ D = \frac{{\lg n}}{{\lg n + \lg \left( {d/L} \right)}} $ | (1) |
式中:n为组成过程线的段数,采用“过程线节点数-1”得到;d为过程线起点到终点的直线距离;L为过程线的总长度,即所有线段长度的累积。分维数的大小表示过程线变化的复杂程度,分维数越大,说明过程变化越复杂。
1.3.2 R/S分析法该分析法(重标极差分析法)由著名水文学家Hurst于1995年首先提出,该方法主要用Hurst指数衡量和描述非线性时间序列的持续性或反持续性,基本原理[12]如下:
设一时间序列:{ζ(t)},t=1,2,3,···,N;然后取一个系列τ=1,2,3,···,N,对于某个τ,定义:
| $ 极差:R\left( \tau \right) = \max \mathop X\limits_{1 \le t \le \tau } \left( {t, \tau } \right) - \min \mathop X\limits_{1 \le t \le \tau } \left( {t, \tau } \right) $ | (2) |
| $ {\rm{11}}:S\left( \tau \right) = \sqrt {\frac{1}{\tau }\sum\limits_{t = 1}^\tau {{{\left( {\zeta \left( t \right) - {{\left\langle \zeta \right\rangle }_\tau }} \right)}^2}} } $ | (3) |
| $ {\rm{Hurst}}指数:\ln \left( {R/S} \right) = H\ln \tau + H\ln a $ | (4) |
Hurst指数的H值一般处于0~1之间:当H >0.5时,全部或部分数据之间满足正相关性或长记忆性,意味着时间序列未来的趋势与过去一致,即这个过程具有持续性,H值越接近1,长记忆性就越强;当H =0.5时,序列中各个数据都是独立的,互不关联,完全随机的,前一段时间的变化趋势不会对后面产生影响;当H < 0.5时,全部或部分数据之间满足负相关性或反记忆性,意味着未来的总体趋势将与过去相反,即这个过程具有反持续性,H值越接近0,反记忆性就越强[10]。
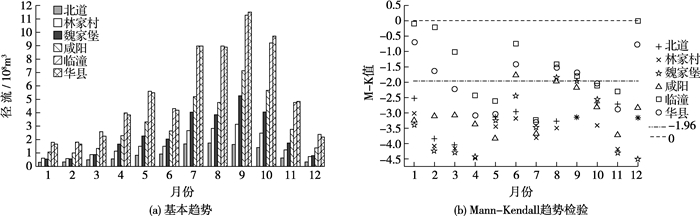
2 结果与分析 2.1 渭河干流月径流量变化特征选取渭河干流的北道、林家村、魏家堡、咸阳、临潼和华县6个主要控制站进行分析,并将其划分为上、中、下游。由图 2(a)可知,渭河干流径流量年内分配不均,主要集中在汛期(6-10月)。从上游到下游,即从北道到临潼站,月径流量依次增加,而从临潼到华县站中有焦口站大量取水,月径流量整体上略有减少。
|
图 2 渭河干流月径流变化趋势 Fig. 2 Variation trend of monthly runoff in mainstream of Weihe River |
图 2(b)为渭河干流月径流量M-K趋势检验。取显著性水平α=0.05,则Zα/2=±1.96。由图 2(b)可知,渭河干流各站点的月径流量均呈减少趋势。上游北道和林家村站月径流量呈显著性减少;中游魏家堡和咸阳站除8月和6月未通过显著性检验外,其余月份均为显著性减少;而下游临潼和华县站的月径流量大多未通过显著性检验。渭河干流所有站点月径流量均呈显著性减少趋势的月数为4, 5, 7, 10和11月。上游站点月径流量减少趋势的显著性大于中游站点,下游站点月径流量减少趋势的显著性最弱。从上游到下游,月径流量减少趋势的显著性越来越弱,呈显著性减少趋势的月份也越来越少。
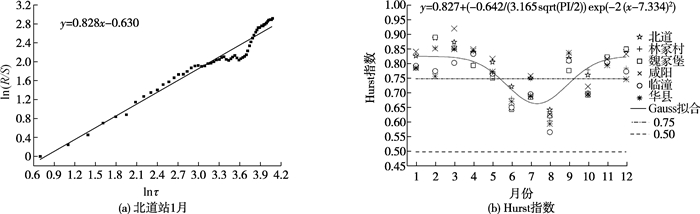
2.2 渭河干流月径流深序列的R/S分析径流深度反映的是流域平均径流水平,用径流深序列进行R/S分析,所得的Hurst指数更具可比性。将处理后的数据进行计算,计算起止时刻取τ=2。以渭河干流上游北道站1月为例,其月径流深R/S分析结果如图 3(a)所示。由图 3(a)可知,北道站1月的分析结果具有很好的线性关系,表明其Hurst效应显著。渭河干流各站点月径流深R/S分析(ln(R/S)- lnτ)的相关系数均在0.86以上,其整体趋势均表现出良好的线性关系,表明各站点的Hurst效应均为显著。
|
图 3 渭河干流月径流深序列R/S分析 Fig. 3 R/S analysis of monthly runoff depth sequence along mainstream of Weihe River |
图 3(b)为渭河干流各站点的月径流深Hurst指数。分析结果表明:渭河干流各站点的月径流深Hurst指数均大于0.5,与历史变化呈正相关性(或持续性),即未来相同时间内各站点的月径流量将呈减少趋势。渭河干流各站点的最小月径流深Hurst指数均集中在汛期的8月,最大Hurst指数集中在非汛期的2—4月。在非汛期(11—5月)和汛期的9月,渭河各站点的月径流深时间序列Hurst指数均大于0.75,呈现出较强的持续性。9月以外的汛期(6—8月、10月),渭河干流有87.5%的月径流深Hurst指数小于0.75,其中除7月和10月的北道和林家村站外,其余的月径流深Hurst指数均小于0.75,呈现出较弱的持续性。运用Gauss方法对渭河干流各站点的月径流深Hurst指数进行联合拟合,通过了95%的显著性检验。由拟合曲线可知,在1—3月,渭河干流各站点的Hurst指数基本不变;在3—8月,渭河干流各站点的Hurst指数总体呈减少趋势;在8—12月,渭河干流各站点的Hurst指数总体呈增长趋势。汛期径流量的Hurst指数整体上小于非汛期。当H >0.5时,H值越接近1,长记忆性就越强,表明未来汛期径流量持续性减少的趋势要小于非汛期。
2.3 渭河干流月径流分维数采用平均值归一化方法对月径流数据进行处理,将处理后的月径流量进行分维数计算,结果如表 1所示。由表 1可知,渭河干流各站点最大分维数集中在汛期(6—10月),最小分维数集中在流域枯水期,这是由于汛期径流量大,河道径流受上游来水量和降雨量影响,其变化过程复杂;而枯水期径流小,降雨量小,河道径流无明显变化,其变化过程简单。渭河干流的月径流分维数为1.025~ 1.116,其中月径流分维数最大值为魏家堡10月,最小值为北道2月。
| 表 1 月径流分维数 Tab. 1 Monthly runoff fractal dimension |
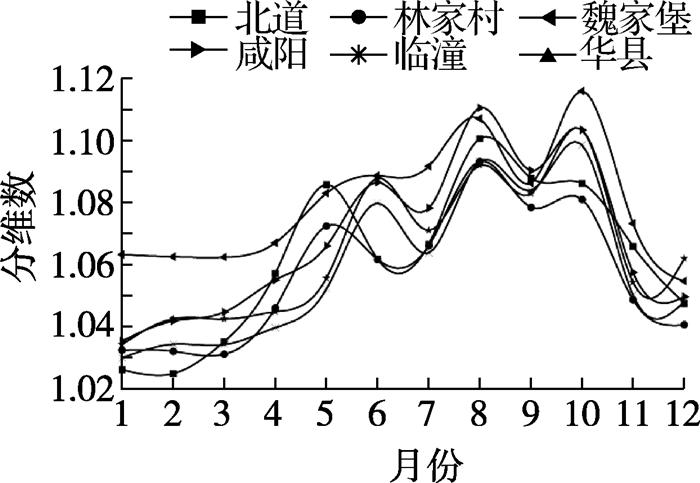
图 4为渭河干流月径流分维数变化趋势。由图 4可知,渭河干流各站点的月径流分维数在7—11月整体变化一致,上、中、下游各流域段中的站点月径流分维数变化趋势一致。这是因为相同流域站点相距较近,气候及所处的地形地貌、地质、土壤等条件相似。上游月径流分维数小于下游月径流分维数,中游月径流分维数最大。这是因为上游径流量小,无较大支流汇入,河道径流变化较小;中游存在着较大、较多的支流汇入,不仅受降雨量的影响,还会受各支流来水的影响;下游较大支流汇入较少,支流大多汇于中游,在下游已趋于平缓,且受支流来水、流域控制区人类活动等多因素的共同作用和调节,下游径流过程趋于平缓,分维数较小[11]。
|
图 4 月径流分维数变化趋势 Fig. 4 Variation trend of monthly runoff fractal dimension |
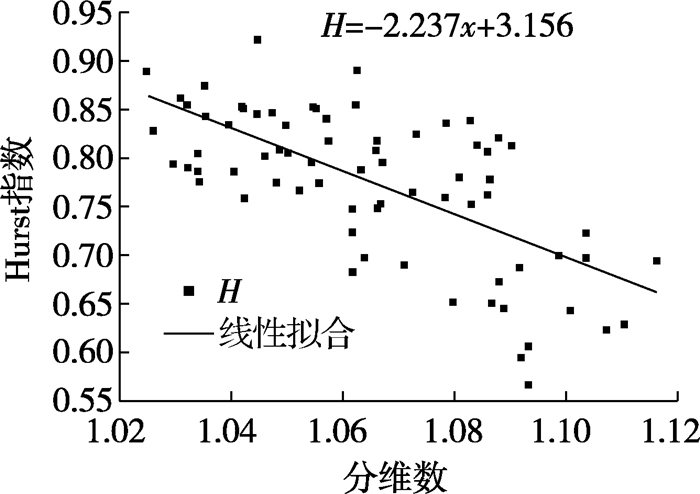
对比分形维数的指数律可知,R/S分析中的指数律与分形论中的标度不变性是一致的,且存在一定的定量关系。为了反映月径流分维数与Hurst指数的关系,将各控制站的月径流分维数作为自变量,相对应的月径流深Hurst指数作为因变量进行分析,结果见图 5。
|
图 5 月径流分维数与Hurst指数一元线性回归 Fig. 5 Unary linear regression of monthly runoff fractal dimension with Hurst index |
月径流分维数与Hurst指数的线性表达式为:H=-2.237x+3.156,其相关系数r=-0.670 4。采用相关系数检验法对上述结果进行显著性检验:f=n-2=70,在显著性水平α=0.05情况下,查表得:f=70时,r0.05=0.231 9。因为|r|=0.670 4>r0.05,所以月径流分维数与Hurst指数之间有着显著负相关关系,即分维数越大,Hurst指数越小。分维数用来反映时间序列的复杂性,因此Hurst指数同样也能反映时间序列的复杂性,即时间序列越复杂,分维数越大,Hurst指数越小。
3 结语(1) 渭河干流径流量年内分配不均,径流量主要集中在汛期(6—10月)。渭河干流各站点的月径流量均为减少趋势,从上游到下游,月径流量减少趋势的显著性越来越弱,呈显著性减少趋势的月份也越来越少。渭河干流各站点的月径流深Hurst指数均大于0.5,皆与历史变化呈正相关性(持续性),即各站点在未来月径流量将呈减少趋势。
(2) 渭河干流各站点最大分维数集中在汛期,最小分维数集中在枯水期;上游分维数小于下游分维数,中游分维数最大。Hurst指数与月径流分形维数之间有着显著的负相关关系,分维数反映时间序列的复杂性,因此Hurst指数同样也能反映时间序列复杂性,即时间序列越复杂,分维数越大,Hurst指数越小。
(3) 汛期径流量的分维数大于非汛期,汛期径流量的Hurst指数小于非汛期,验证了Hurst指数与月径流分形维数之间有着显著的负相关关系。分维数越大,径流过程变化越复杂,河流调节能力越差,即汛期的径流变化复杂程度大于非汛期,中游的径流变化复杂程度大于上下游,表明汛期和中游的河流径流量调节能力相对较差。因此,相关部门应重视汛期和中游的径流量变化情况,制定合理的流域水资源严格管理对策,提前做好安全防范工作。
| [1] |
HUANG S Z, LIU D F, HUANG Q, et al. Contributions of climate variability and human activities to the variation of runoff in the Wei River Basin, China[J]. International Association of Scientific Hydrology Bulletin, 2016, 61(6): 1026-1039. DOI:10.1080/02626667.2014.959955 |
| [2] |
孙悦, 李栋梁. 1975-2011年渭河上游径流演变规律及对气候驱动因子的响应[J]. 冰川冻土, 2014, 36(2): 413-423. ( SUN Yue, LI Dongliang. Features and response to climate-driven factors of the runoff in the upper reaches of the Weihe River in 1975-2011[J]. Journal of Glaciology and Geocryology, 2014, 36(2): 413-423. (in Chinese)) |
| [3] |
李斌, 解建仓, 胡彦华, 等. 渭河中下游年径流量变化趋势及突变分析[J]. 水利水运工程学报, 2016(3): 61-69. ( LI Bin, XIE Jiancang, HU Yanhua, et al. Analysis of variation and abruption of annual runoff in middle and lower Weihe[J]. Hydro-Science and Engineering, 2016(3): 61-69. (in Chinese)) |
| [4] |
NI Z H, WU L C, WANG M H, et al. The fractal dimension of river length based on the observed data[J]. Journal of Applied Mathematics, 2013, 1-9. |
| [5] |
ZHAO X H, CHEN X, HUANG Q. Trend and long-range correlation characteristics analysis of runoff in upper Fenhe River Basin[J]. Water Resources, 2017, 44(1): 31-42. DOI:10.1134/S0097807817010201 |
| [6] |
FACBENEDA J. Fractal structure of the kashubian hydrographic system[J]. Journal of Hydrology, 2013, 448: 48-54. |
| [7] |
李国栋, 张俊华, 王乃昂, 等. 基于重标极差分析和非周期循环分析的气候变化趋势预测--以兰州市为例[J]. 干旱区研究, 2013, 30(2): 299-307. ( LI Guodong, ZHANG Junhua, WANG Naiang, et al. Calculation of climate change trend based on the analysis of averages and aperiodic cyclic analysis: A case study of Lanzhou City[J]. Arid Zone Research, 2013, 30(2): 299-307. (in Chinese)) |
| [8] |
赵辉, 郭索彦, 解明曙, 等. 不同尺度流域日径流分形特征[J]. 应用生态学报, 2011, 22(1): 159-164. ( ZHAO Hui, GUO Suoyan, XIE Mingshu, et al. Fractal characteristics of daily discharge in different scales watersheds[J]. Chinese Journal of Applied Ecology, 2011, 22(1): 159-164. (in Chinese)) |
| [9] |
张涵丹, 卫伟, 薛萐, 等. 基于R/S分析和Mann-Kendall检验的定西市气温降水变化特征[J]. 水土保持研究, 2015, 22(6): 183-189. ( ZHANG Handan, WEI Wei, XUE Sha, et al. Analysis on the variation of temperature and precipitation in Dingxi based on R/S and Mann-Kendall test[J]. Research of Soil and Water Conservation, 2015, 22(6): 183-189. (in Chinese)) |
| [10] |
潘国营, 秦永泰, 马亚芬, 等. 基于R/S和Morlet小波分析的丹河径流变化特征研究[J]. 水资源与水工程学报, 2015, 26(3): 41-45. ( PAN Guoying, QIN Yongtai, MA Yafen, et al. Research on variation characteristics of runoff in Danhe river basin based on R/S and Morlet wavelet analysis[J]. Journal of Water Resources and Water Engineering, 2015, 26(3): 41-45. (in Chinese)) |
| [11] |
冯小庆, 严宝文. 渭河流域径流过程的分形特征研究[J]. 灌溉排水学报, 2011, 30(5): 103-107. ( FENG Xiaoqing, YAN Baowen. Fractal characteristics of runoff process in Weihe watershed[J]. Journal of Irrigation and Drainage, 2011, 30(5): 103-107. (in Chinese)) |
| [12] |
马宗伟, 许有鹏, 钟善锦. 水系分形特征对流域径流特性的影响-以赣江中上游流域为例[J]. 长江流域资源与环境, 2009, 18(2): 163-169. ( MA Zongwei, XU Youpeng, ZHONG Shanjin. Influence of river network fractal characteristic of runoff-case study in the basin of upper and middle courses of Gan River[J]. Resources and Environment in the Yangtze Basin, 2009, 18(2): 163-169. DOI:10.3969/j.issn.1004-8227.2009.02.012 (in Chinese)) |
| [13] |
李建林, 昝明军, 李宝玲. 基于R/S分析的黑河出山年径流量灰色预测[J]. 地域研究与开发, 2014, 33(5): 127-131. ( LI Jianlin, ZAN Mingjun, LI Baoling. Grey prediction of out-mountainous annual runoff of Heihe River based on R/S analysis[J]. Areal Research and Development, 2014, 33(5): 127-131. DOI:10.3969/j.issn.1003-2363.2014.05.024 (in Chinese)) |
| [14] |
SONG X, ZHANG J, AGHAKOUCHAK A, et al. Rapid urbanization and changes in spatiotemporal characteristics of precipitation in Beijing metropolitan area[J]. Journal of Geophysical Research, 2014, 119(19): 11250-11271. |
| [15] |
张利茹, 贺永会, 唐跃平, 等. 海河流域径流变化趋势及其归因分析[J]. 水利水运工程学报, 2017(4): 59-66. ( ZHANG Liru, HE Yonghui, TANG Yueping, et al. Analysis of runoff change trend and its attribution in Haihe River basin[J]. Hydro-Science and Engineering, 2017(4): 59-66. (in Chinese)) |
2. River Basin Administration Bureau in Shaanxi, Xi'an 710018, China
 2019
2019 
