2. 重庆交通大学 水利水运工程教育部重点实验室,重庆 400074;
3. 浙江禹瑞工程咨询有限公司,浙江 杭州 310051
山区河流床面多由原生基岩或卵砾石组成,河道中亦常见江心洲、石梁、礁石或卵石沙波等,这些粗糙元素的高度与水深往往较为接近或具有相同的数量级,形成大尺度粗糙[1-2]。按粗糙元素排列方式的不同,大尺度粗糙床面可分为密排粗糙和散粒粗糙2类,散粒粗糙又包括粗糙单元孤立分布(散粒体)和阵列分布2种情况。粗糙单元孤立分布成为散粒体后,其周围常伴随次生流等复杂流态,造成通航河流河床结构和水流条件的变化,影响船舶航行安全;同时,大尺度散粒体也易对相邻的小尺度颗粒(如泥沙、卵石等)形成遮蔽效应,在周围复杂水流结构的耦合作用下,改变颗粒起动输移特性与河床演变规律。因此,研究大尺度散粒体周围水流结构,对改善航道和维护河相等具有重要的现实意义。
目前,人们对大尺度散粒粗糙床面明渠水流结构开展了一些研究。20世纪Keulegan提出明渠水流纵向时均流速沿水深满足对数分布,但通过进一步的研究发现,垂线流速分布会随着床面粗糙尺度的不同而变化。何建京等[3]认为,粗糙床面明渠均匀流的垂线流速分布服从对数公式,但非均匀流的流速分布不能采用单一的对数公式描述。Byrd等[4]测量了天然河流粗糙床面的水流流速,发现仅有约10%的垂线流速符合对数分布,大部分流速垂线分布形态呈不规则、直线和S形。Wang等[5]提出明渠水流满足Δ/R>0.15,Fr>0.47,Re>60 000条件时(Δ为粗糙元素高度,R为水力半径,Fr为弗劳德数,Re为雷诺数),流速分布将呈S形。Papanicolaou等[6]认为中尺度均布粗糙时(h/dc=2.5,dc为球体直径),球体周围流速不再遵循对数分布,而更满足速度亏损律[7],同时,靠近床面的回流延伸至球体后方1.5dc,散粒体对平均流速分布的影响可达3.5dc,Uchida等[8]提出了一种计算散粒体周围流速分布的新方法。Baki等[9]基于斜坡鱼道水流流动的角度,将圆形石块按梅花形排列铺于槽底,研究了3种底坡下粗糙床面的水面形态及流速垂线分布规律。Shamloo等[10]从河流生境结构的角度,根据相对水深划分了4种情况,研究了半球体周围水流结构,Tritico等[11]基于野外原型观测资料拓展了相关研究。Lacey等[12-13]通过对山区卵石河床的原型观测,探讨了大尺度粗糙元素对水流结构影响较强烈的区域,分析了粗糙床面下立方体周围水流结构随相对水深的变化规律。
需要指出,上述研究主要针对某种特定形态散粒体及其集群分布排列对水流结构的影响,天然河流床面散粒粗糙形态各异,但目前仍缺乏不同形态散粒体周围水流结构的对比研究。为此,本文结合山区河流河床孤礁的实际形状,将散粒体概化为正方体、球体和四面体3种形态进行水槽试验,基于声学多普勒流速仪获得的瞬时流速资料,开展大尺度散粒体周围水流结构研究,研究成果将有助于深化大尺度散粒体周围水流结构的规律认识,并可为山区河流开发保护和航道整治工程设计等提供参考。
1 水槽试验试验在重庆交通大学国家内河航道整治工程技术研究中心进行,主要试验装置设备包括高精度整体变坡水槽、水位测针、电磁流量计和Vectrino声学多普勒点式流速仪(简称“高级小威龙流速仪”)等。高精度整体变坡水槽长L=28 m、宽B=0.56 m、高H=0.50 m,水槽侧面和底面均由3.3 m长的玻璃板组成,玻璃安装误差小于0.2 mm,水槽全长误差小于0.5 mm,结构变形小于0.3 mm。水槽底坡可通过电机传动装置自动调整,变坡范围-1‰ ~7‰。水槽配备了由大小水泵、变频器、流量计组成的2套水循环系统,最大供水流量120 L/s。
试验采用了高度均为Δ=5 cm的正方体、球体和四面体3种形态散粒体(正方体边长和球体直径均为5 cm,四面体边长5.6 cm),均采用混凝土制作。试验时将散粒体置于水槽纵向中轴线(图 1),其中正方体迎流面为正方形,球体迎流面为圆形,四面体迎流面为三角形,试验段位于水槽下游;试验时固定流量和底坡,通过调节尾门开度使散粒体断面水深保持一致,散粒体距水槽进口断面20 m,确保来流平顺并接近均匀流,距水槽出口断面8 m,可使其周围水流结构得以充分发展。研究中共进行了6组试验,试验水流为恒定流,流量Q采用电磁流量计控制,水深h通过尾门控制,试验中保持散粒体断面水深h=9 cm和底坡i=0.003不变,试验工况参数见表 1;同时为与散粒体处于非淹没时的水面形态进行对比,试验中观测记录了水深h=4.5 cm时的水面形态。宽深比B/h=6.22>5,满足二维水流条件;散粒体顶部到水面距离HT与颗粒高度Δ的比值HT/Δ=0.8,满足王晋军[1]提出的大尺度粗糙条件(HT/Δ≤1.0)。

|
图 1 散粒体形态及水槽试验 Fig. 1 Artificial roughness morphology and flume test |
| 表 1 试验工况 Tab. 1 Experimental conditions |
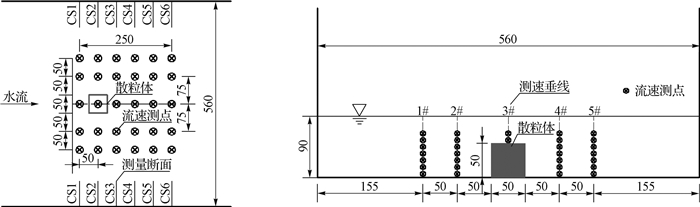
流速测点沿散粒体周围左右对称布置(见图 2,以正方体为例),沿水流方向共布置6个测流断面(CS1-CS6),散粒体轴线位于CS2断面,上游CS1断面距散粒体轴线5 cm,下游CS3~CS6断面距散粒体轴线分别为5,10,15和20 cm;每个断面沿槽宽方向均布设5条测流垂线(1#~5#),垂线间距5.0~7.5 cm;流速采集的水深范围0.5~6.5 cm,垂向测点间距1.0 cm,其中散粒体顶部垂线布置2个测点,其余各垂线布置7个测点。流速数据应用高级小威龙流速仪采集,可测最大测速4 m/s,测量精度±1 mm/s,采样体积中心距离发射器5.0 cm。通过对预备试验流速实测结果的分析,确定采样频率100 Hz,单点采样数10 000个。由于信噪比(SNR)和相关系数(COR)对流速数据质量影响显著,根据相关要求,本文选用了SNR≥15 dB,COR≥70%的流速数据,并采用改进椭圆阈值法[14]对流速数据进行了毛刺剔除和滤波处理。
|
图 2 流速测点布置(单位:mm) Fig. 2 Arrangement of velocity measuring points(unit: mm) |
图 3给出了水深h=4.5 cm、散粒体处于非淹没状态时的水面形态,图 4给出了水深h=9.0 cm、散粒体处于淹没状态时的水面形态。结果显示:(1)水深h较小,h/Δ=0.9,散粒体处于非淹没状态时,水流绕过散粒体发生侧向流动,并在散粒体后方形成漩涡区,绕流现象较为明显,且不同形态散粒体的绕流现象存在差异;正方体正后方水流呈V形扩散,从颗粒顶部向两侧绕流形成U形波状;球体周围水流呈U形扩散;四面体正后方水流呈三角形扩散,两侧为U形,但范围较正方体时更小。(2)水深增大,h/Δ=1.8,散粒体处于淹没状态时,绕流现象变得更不明显,但水流越过散粒体后水面下降,在其下游产生波状起伏;上游水流经过散粒体时,水深减小,比降增大,流速开始逐渐增大,由于惯性力作用,主流进一步收缩,直至散粒体下游收缩断面处,此时过水面积最小,流速达到最大;由于散粒体所占空间不过流,水流移向两侧发生横流,横流与纵向水流叠加,形成了马蹄形的绕流波动,其两侧分离点随水位降低而延展;其他条件相同时,散粒体阻水面积越大,上游壅水高度和下游绕流影响范围越大。

|
图 3 非淹没状态时的水面形态 Fig. 3 Surface morphology of non-submerged state |

|
图 4 淹没状态时的水面形态 Fig. 4 Surface morphology of submerged state |
试验数据表明,各工况的垂向流速小于纵向流速和横向流速,这里重点分析纵向和横向流速的分布情况。为便于对比,对相关物理量进行了无量纲化处理;各方向流速(纵向流速u、横向流速v、合流速Um)均采用试验流速进行无量纲化,试验流速选用工况2的散粒体所在断面平均流速(U=39.1 cm/s);沿程位置x和沿槽宽位置y均采用散粒体高度Δ进行无量纲化,x+=x/Δ,y+=y/Δ;散粒体中心x+= 0,y+= 0,散粒体上游x+ < 0,下游x+> 0,顺水流向散粒体右侧y+ < 0,左侧y+> 0;垂向位置z采用散粒体处水深h进行无量纲化,η=z/h,水底η=0,水面η=1。
2.2.1 平面合流速由前文介绍可知,流速采集的水深范围0.5~6.5 cm,平面流速分层根据流速测量情况考虑,并取η=0.72为表层,η=0.39为中层,η=0.06为底层。
数据显示,表层纵向流速与表层合流速的云图分布形态较为相似。图 5给出了各试验工况表层合流速Um/U的平面分布云图,结果显示:(1)在保持其他参数不变的情况下,表层合流速Um/U随Fr和散粒体阻水面积的增大而增大,Um/U基本以散粒体纵轴线左右对称分布,高速区主要出现在散粒体平面形心附近,并向下游方向延伸;Fr越大,散粒体的阻水作用越明显,高速区流速及范围越大,最大流速可达试验流速的1.3倍。(2)散粒体形态对流速分布有较大影响。当Fr较小时(Fr=0.211),受水槽来流量限制,散粒体后方并未发生明显的水位波动;颗粒阻水面积越大,最大流速和影响范围越大;正方体形心处存在流速最大值,之后流速迅速降低;球体和四面体形心处Um/U降到最低,平面上呈菱形分布,高速区在x+= 1附近。(3)当Fr较大时(Fr=0.416),正方体周围Um/U分布呈向下游扩散的等腰梯形,形心后方(1.5~2.5)Δ处存在菱形旋涡区,宽约2 Δ;球体周围Um/U分布则呈向下游收缩的钟形,流速梯度分布较均匀;四面体周围最大流速位置相对于前两者向下游移动了约Δ的距离,流速分布呈不规则菱形。主流经束窄后扩散,流速经过先增大再减小的过程,在散粒体形心后方3 Δ处存在流速收缩断面。由于正方体颗粒对流速影响范围较大,流速收缩断面较其余2种散粒体更不明显。

|
图 5 表层合流速Um/U分布 Fig. 5 Resultant velocity Um/U distribution in surface layer |
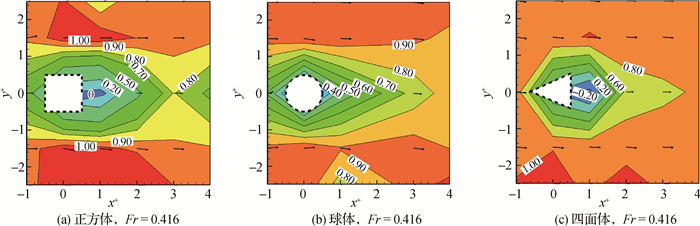
试验资料显示,不同Fr时对应的中层、底层合流速形态分布较为一致,为节省篇幅,图 6和图 7重点给出了Fr=0.416(工况2,4,6)时,中层及底层合流速Um/U的平面分布云图。分析表明:(1)散粒体阻水面积越大,其流速影响范围越大,流速基本以散粒体纵轴呈对称分布;不同散粒体周围的流速分布总体形态较为相似,周围Δ范围内流速分布呈条带状,其后方流速分布均呈向下游延伸的三角形,横向影响范围约为2.5 Δ。(2)在中层平面,由于散粒体不过流,散粒体所在位置流速为0,并且流速向下游方向逐渐增大为试验流速。(3)在底层平面,流速分布与中层较为相似,但流速相对较小,且在散粒体后方流速出现负值,说明在靠近水槽底部位置存在水流回流区。

|
图 6 中层合流速Um/U分布 Fig. 6 Resultant velocity Um/U distribution in middle layer |
|
图 7 底层合流速Um/U分布 Fig. 7 Resultant velocity Um/U distribution in bottom layer |
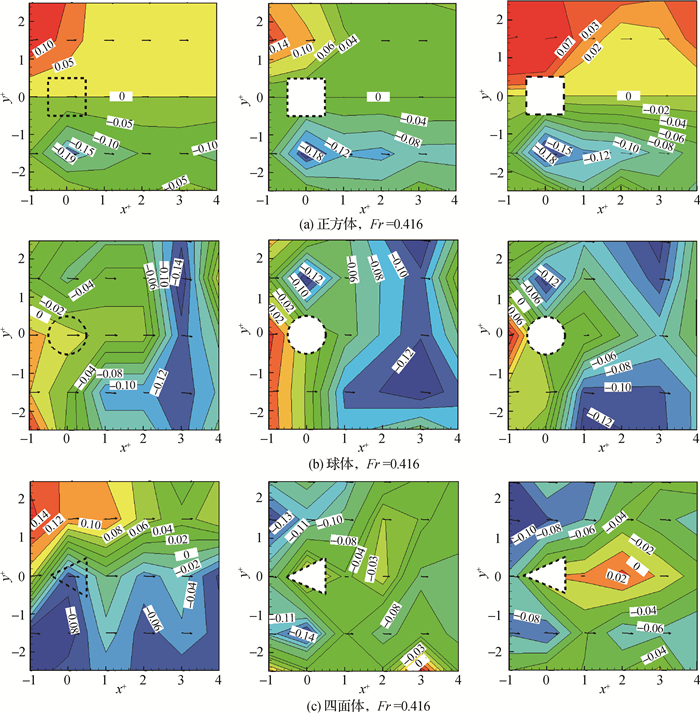
不同散粒体周围横向流速的差异随弗劳德数的增大而愈加明显,因此,图 8重点给出了Fr=0.416时(工况2,4,6)相对横向流速v/U的平面分布云图,从左至右依次对应表层、中层和底层,流速方向以指向水槽左侧为正,指向水槽右侧为负。
|
图 8 横向流速v/U平面分布 Fig. 8 Transverse velocity v/U distribution in surface layer |
由图 8可见:(1)正方体与球体周围v/U大小及分布形态随水深变化较小,正方体两侧v/U在数值上表现出一正一负,即水流绕过正方体后将向两侧流动,v/U由纵向中轴剖面指向两侧边壁逐渐增大,强横流区位于平面形心右侧1.5 Δ位置,呈菱形分布,最大横流达到试验流速的19%。(2)球体周围v/U沿水流方向逐渐增大,形心后方3 Δ断面附近为强横流区。(3)四面体周围表层v/U与正方体时的分布趋势相似,水流绕流后也向两侧流动,但v/U沿水流方向逐渐减小。中层和底层v/U分布较为紊乱,带状结构不明显。
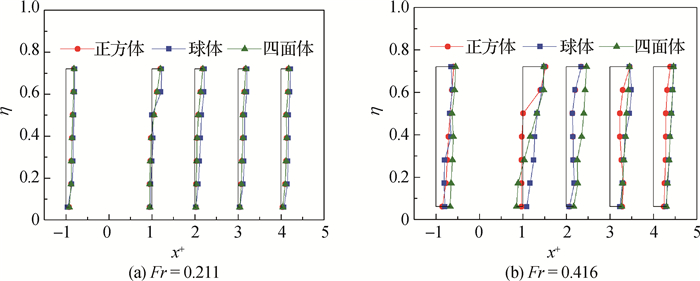
2.3 纵剖面流速分布这里重点探讨纵向中轴剖面上各垂线的无量纲纵向流速u/U沿程分布。图 9给出了不同Fr时u/U的垂线分布,图 10给出了不同散粒体形态时u/U的垂线分布。

|
图 9 不同Fr时u/U的垂线分布 Fig. 9 Vertical distribution variation of u/U with different Fr |
|
图 10 不同散粒体形态时u/U的垂线分布 Fig. 10 Vertical distribution variation of u/U with different artificial roughness elements |
由图 9~10可见:(1)同一散粒体不同工况下的u/U垂线分布规律基本一致;正方体上游u/U与指数分布规律更为吻合,下游2 Δ与3 Δ处u/U垂线分布呈S型,4 Δ处u/U垂线分布接近线性;球体的u/U垂线分布较不规则,在Fr较大时下游1 Δ处u/U垂线分布呈线性,2 Δ处呈S型分布,3 Δ与4 Δ处接近线性;四面体下游1 Δ处u/U垂线分布呈S型,2 Δ及更远处基本呈线性分布。(2)当Fr=0.211时,3种散粒体的u/U垂线分布差异较小,其上游u/U垂线分布与指数分布规律更为吻合,下游1 Δ处的u/U垂线变化较明显,由于散粒体不过流,流速从水深0.6 h处骤减,在靠近水槽底部为负值,此后u/U垂线分布逐渐恢复为指数分布,散粒体对u/U垂线分布的影响沿水流方向逐渐减弱。Fr增大后,散粒体对u/U垂线分布影响的差异逐渐增强,u/U垂线分布不再遵循指数分布;正方体下游1 Δ处在η=0.5附近流速骤减为0;球体下游流速呈先增大后减小再增大的变化趋势;四面体下游1 Δ处近底位置存在明显回流。
3 结语(1) 3种散粒体单体水槽试验显示,水深h较小,h/Δ=0.9,散粒体处于非淹没状态时,其周围水流呈U形向下游扩散,正方体的横流区范围最大,球体次之,四面体最小;水深增大,h/Δ=1.8,散粒体处于淹没状态时,其周围横流将明显减弱,水流越过散粒体后在下游形成波状起伏。
(2) 本文试验范围内,表层合流速Um/U平面分布受水流弗劳德数Fr的影响较大,而中、底层Um/U平面分布受Fr影响很小;表层Um/U随Fr和散粒体阻水面积的增大而增大,Fr较大时,高速区主要出现在散粒体平面形心附近,最大值可达试验流速的1.3倍,正方体、球体和四面体对应的表层Um/U平面分布分别呈等腰梯形、钟形和菱形;强横流区位于散粒体形心两侧1.5 Δ范围内,最大横流可达试验流速的19%。
(3) Fr较小时,散粒体对纵向流速u/U垂线分布的影响较小,上游断面u/U与指数分布规律吻合,下游1 Δ处u/U垂线分布变化较明显,流速从水深0.6 h处骤减,在靠近水槽底部为负值,此后u/U垂线分布逐渐恢复为指数分布;Fr增大后,散粒体对u/U垂线分布影响的差异逐渐增强,u/U垂线分布不再遵循指数分布。
(4) 大尺度散粒体周围水流结构影响因素复杂,本文主要探讨了散粒体形态和弗劳德数Fr对水流结构的影响,今后可进一步考虑底坡、散粒体排列方式等多种因素变化情况,以深化散粒体周围水流结构认识。
| [1] |
王晋军. 大尺度粗糙水流特性初探[J]. 水利学报, 1993(1): 68-71, 79. ( WANG Jinjun. A preliminary study on the channel flow characteristics with large scale roughness[J]. Journal of Hydraulic Engineering, 1993(1): 68-71, 79. DOI:10.3321/j.issn:0559-9350.1993.01.011 (in Chinese)) |
| [2] |
韩正国.大尺度粗糙床面明渠水流结构及阻力特性研究.重庆: 重庆交通大学, 2017. (HAN Zhengguo. Flow structure and resistance characteristics of open channel with large scale rough bed. Chongqing: Chongqing Jiaotong University, 2017. (in Chinese))
|
| [3] |
何建京, 王惠民. 粗糙床面明渠水力特性研究[J]. 水利水运工程学报, 2004(3): 19-23. ( HE Jianjing, WANG Huimin. Hydraulic characteristics of open channel flow over a rough bed[J]. Hydro-Science and Engineering, 2004(3): 19-23. DOI:10.3969/j.issn.1009-640X.2004.03.004 (in Chinese)) |
| [4] |
BYRD T C, FURBISH D J, WARBURTON J. Estimating depth-averaged velocities in rough channels[J]. Earth Surface Processes and Landforms, 2000, 25(2): 167-173. DOI:10.1002/(ISSN)1096-9837 |
| [5] |
WANG X K, YE C, WANG B J, et al. Experimental study on velocity profiles with different roughness elements in a flume[J]. Acta Geophysica, 2015, 63(6): 1685-1705. DOI:10.1515/acgeo-2015-0063 |
| [6] |
PAPANICOLAOU A N, KRAMER C M, TSAKIRIS A G, et al. Effects of a fully submerged boulder within a boulder array on the mean and turbulent flow fields: Implications to bedload transport[J]. Acta Geophysica, 2012, 60(6): 1502-1546. DOI:10.2478/s11600-012-0044-6 |
| [7] |
DEY S, RAIKAR R V. Characteristics of loose rough boundary streams at near-threshold[J]. Journal of Hydraulic Engineering, 2007, 133(3): 288-304. DOI:10.1061/(ASCE)0733-9429(2007)133:3(288) |
| [8] |
UCHIDA T, FUKUOKA S, PAPANICOLAOU A N, et al. Nonhydrostatic Quasi-3D model coupled with the dynamic rough wall law for simulating flow over a rough bed with submerged boulders[J]. Journal of Hydraulic Engineering, 2016, 142(11): 04016054. DOI:10.1061/(ASCE)HY.1943-7900.0001198 |
| [9] |
BAKI A B M, ZHU D Z, RAJARATNAM N. Mean flow characteristics in a Rock-Ramp-Type fish pass[J]. Journal of Hydraulic Engineering, 2014, 140(2): 156-168. DOI:10.1061/(ASCE)HY.1943-7900.0000816 |
| [10] |
SHAMLOO H, RAJARATNAM N, KATOPODIS C. Hydraulics of simple habitat structure[J]. Journal of Hydraulic Research, 2001, 39(4): 351-366. DOI:10.1080/00221680109499840 |
| [11] |
TRITICO H M, HOTCHKISS R H. Unobstructed and obstructed turbulent flow in gravel bed rivers[J]. Journal of Hydraulic Engineering, 2005, 131(8): 635-645. DOI:10.1061/(ASCE)0733-9429(2005)131:8(635) |
| [12] |
LACEY R W J, ROY A G. The spatial characterization of turbulence around large roughness elements in a gravel-bed river[J]. Geomorphology, 2008, 102(3-4): 542-553. DOI:10.1016/j.geomorph.2008.05.045 |
| [13] |
LACEY R W J, RENNIE C D. Laboratory investigation of turbulent flow structure around a bed-mounted cube at multiple flow stages[J]. Journal of Hydraulic Engineering, 2012, 138(1): 71-84. |
| [14] |
GORING D G, NIKORA V I. Despiking acoustic doppler velocimeter data[J]. Journal of Hydraulic Engineering, 2002, 128(1): 117-126. |
2. Key Laboratory of Hydraulic and Waterway Engineering of the Ministry of Education, Chongqing Jiaotong University, Chongqing 400074, China;
3. Zhejiang Yurui Engineering Consulting Co., Ltd., Hangzhou 310051, China
 2019
2019 