2. 国网陕西安康水力发电厂,陕西 安康 725000
黄河上游是指河源至内蒙古的托克托县河口镇河段,为黄河水量的主要来源区域,径流量占黄河全年径流总量的60%以上[1-2]。黄河上游水沙关系变化最为复杂、河道形态演变最为剧烈的河段为宁蒙河段,穿越我国四大沙漠(河东沙地、腾格里沙漠、库布齐沙漠、乌兰布和沙漠),长约1 237 km,地处兰州下游,是典型的沙漠宽谷河段[3-4]。近50年来,随着沿黄地区经济社会的高速发展,水资源供需矛盾日益突出;且极端气候频发、生态环境脆弱,径流量呈减小趋势,致使宁蒙河段不协调的水沙关系进一步恶化,河槽淤积萎缩,形成了长达268 km的“新悬河”[5-6]。悬河主槽过流能力下降,极易导致宁蒙河段小水致大灾,洪水漫滩概率增大、凌灾发生更为频繁,严重威胁防洪防凌安全,危及下游人民生命财产安全[7]。
面对黄河日益严峻的泥沙淤积问题,我国学者先后从水库调度、水沙模型、调沙水量等多个层面出发开展了诸多理论研究。2002年,李国英[8]提出利用水库调水调沙,将不协调的水沙关系调节为相协调的水沙关系,减轻下游河道淤积甚至冲刷下游河道;2007年,胡春宏等[9]分析了黄河水沙过程及其分布变化,构建了黄河流域水沙优化配置方法的理论框架;2009年,张明等[10]研究了河流调水调沙对于减轻下游河段泥沙淤积状况的积极作用,并指出在非饱和状态下泄产生的洪水可对河段产生较好的冲淤效果,增大河段过流能力;2013年,纪昌明等[11]采用全局搜索能力和收敛性较强的鲶鱼效应粒子群算法建立并求解了水库水沙多目标优化调度模型;2015年,白夏等[12]对黄河上游可调输沙水量进行了估算,表明在满足综合用水的情况下,黄河上游有一定富余水量可用于冲淤减沙;2016年,白涛等[13]建立了黄河上游的水沙调控单-多目标调度模型,推荐以较小的电量损失换取输沙量的大幅增加,从而达到显著的水沙调控效果。2017年,姚文艺等[14]分析了龙羊峡、刘家峡水库联合运用对径流泥沙过程的调节作用及其影响,揭示了水库运用对黄河上游水沙关系的调控机制。在实践方面,黄河下游小浪底水库从2002年便开始实施调水调沙,实现了小浪底以下至入海口黄河河道主河槽的全线冲刷,河槽过流输沙能力得到明显提高[15]。上述理论和实践为黄河上游调水调沙奠定了基础和支撑,未来利用梯级水库调水调沙已然成为缓解宁蒙河段河道泥沙淤积的必要措施。而黄河上游具有较大调节性能的水库为龙羊峡、刘家峡等梯级水库,其现有的库容规模能否满足未来长系列调水调沙及其他用水需求,是本文要解决的核心问题。
与此同时,黄河上游龙羊峡水库还是未来南水北调西线工程的受水水库,西线工程的总体规划分为3期[16]:第1期工程从大渡河到雅砻江之间的共5条支流向黄河上游调水40亿m3,第2期工程为从雅砻江干流调水50亿m3,第3期工程为从金沙江调水80亿m3,3期工程共调水170亿m3。虽然目前西线工程的实施进展缓慢,但未来其对于黄河上游的水资源利用形势将产生重大影响,势必也将为调水调沙、发电、供水等目标带来助力。未来西线工程的实施与调水量级的逐渐加大,将会对黄河上游梯级水库的库容规模提出怎样的要求,是本文要回答的关键问题。
鉴于此,开展考虑调水调沙及西线调水的黄河上游梯级水库合理库容研究(本文所提库容均指兴利库容),首先模拟现状年及远景年龙羊峡、刘家峡梯级水库满足防洪、防凌、供水、发电、调水调沙多个用水需求的长系列运行过程;其次分析调水调沙及西线调水对供水、发电等效益的影响;推求满足水资源综合利用的梯级水库合理库容,定量分析调水调沙及西线工程对其影响;最后论证现有的龙羊峡、刘家峡水库库容规模是否能够满足未来新形势下的水资源利用要求。研究结果可为合理布局黄河上游梯级水库的工程规模、科学指导上游水库调水调沙、有效缓解宁蒙河段泥沙淤积等方面提供理论依据和技术支撑。
1 龙羊峡、刘家峡水库联合调度模型 1.1 方案设置龙羊峡、刘家峡水库联合调度方案设置主要考虑以下3个方面,方案设置具体详见表 1。
| 表 1 方案设置 Table 1 Setting schemes |
(1) 现状年及远景年综合用水不同。考虑随着沿黄地区社会经济的发展,未来“三生”综合用水量的提高对梯级水库所需库容规模的影响。以现状及未来兰州断面需水量的不同为依据,设定现状年为2010年,远景年为2030年。
(2) 南水北调西线工程的调水量级不同。考虑未来西线工程的实施及调水量级的逐步增大,对黄河上游调水调沙和梯级水库合理库容的影响。设置远景年西线调水分为无调水、调水40亿m3、调水80亿m3。
(3) 调沙与不调沙的对比。为了量化长系列调水调沙对其他综合效益的影响及其对龙羊峡、刘家峡梯级水库合理库容的要求,设置调沙与不调沙两种对比方案。
1.2 数据资料(1) 来水资料。来水包括天然径流及西线调水过程两部分。①天然径流:1956—2010年共55年逐月黄河上游唐乃亥水文站天然来水资料;龙羊峡至刘家峡区间入流及刘家峡至兰州断面区间入流。②西线调水40亿m3及80亿m3,除每年的12月份为检修月份外,其余月份按平均分配叠加至龙羊峡入库过程中。
(2) 需水资料。兰州断面是黄河上游控制“三生”用水的供水控制断面,因此以兰州断面需水过程作为需水资料。①现状年2010年兰州断面需水过程按照“八七”分水方案确定。②远景年2030年兰州断面需水过程根据《黄河流域综合规划(2012—2030年)》[17],综合考虑未来经济发展趋势、工农业产业结构调整、黄河流域人口增减趋势、黄河流域水资源承载能力;在强节水模式下预测2030年南水北调西线工程不同调水量级下的兰州断面需水过程,原则上为随着调水量级的增加而提高兰州断面需水,以缓解黄河流域的缺水程度。需水资料详见表 2。
| 表 2 现状年及远景年兰州断面需水过程 Table 2 Process of water demand in Lanzhou section |
(3) 水库参数。龙羊峡、刘家峡水库特征参数见表 3。
| 表 3 龙羊峡、刘家峡水库特征参数 Table 3 Characteristic parameters of Longyangxia and Liujiaxia reservoirs |
(4) 调水调沙参数。本文中黄河上游梯级水库进行调水调沙的时机与调沙力度引用黄河上游沙漠宽谷河段水沙调控研究成果[18],为与下游小浪底6月份的调水调沙衔接,上游梯级水库的调水调沙时机选为4月,调沙流量为2 580 m3/s。经测试,方案2和4由于无西线工程水量补充,黄河上游不能进行较长历时的调水调沙,否则将导致后续供水、发电的长期破坏;而方案6和8由于有西线工程的水量补充,可进行1次历时30 d的调水调沙,因此各方案调沙力度(即1次调沙历时)有所不同:方案2和4调沙力度为15 d(4月上半月),方案6和8调沙力度为30 d。
1.3 模型建立 1.3.1 目标函数多年调节水库的库容规模主要取决于连续枯水年组(年调节水库为供水期)的最大累积亏水量,为寻求满足综合用水要求的梯级水库最小库容规模,模型的目标函数为梯级水库缺水量最小,梯级水库长系列调水调沙的实施则以调沙触发条件为判断依据。
| $ {W_{\rm{q}}} = \min \sum\limits_{i = 1}^I {\sum\limits_{j = 1}^J {\left( {k\left( {i,j} \right){Q_{\rm{P}}}\left( {i,j} \right) - {Q_{\rm{G}}}\left( {i,j} \right)} \right)} } \times t\left( {i,j} \right)) $ | (1) |
式中:Wq为梯级水库的最小缺水量(m3/s);i为日历年编号,i=1, 2, …, 55;j为1个日历年的时段编号,j=1, 2, …, 12(以月为单位时段),特别地,方案2和4的日历年4月细分为上半月与下半月两个时段,其余月份仍以月为单位时段,故方案2和4中j=1, 2, …, 13;t(i, j)为计算时段长度(s);QP(i, j), QG(i, j)分别为兰州断面时段需水流量与实际供水流量(m3/s);k(i, j)为缺水判别系数,当(QP(i, j)-QG(i, j))>0时,k(i, j)=1,当(QP(i, j)-QG(i, j))≤0时,k(i, j)=0。
1.3.2 梯级水库调水调沙触发条件梯级水库调水调沙的触发条件为长系列运行中可调沙年份4月初的梯级水库总蓄水量大于1次调沙所需水量,且不导致后续时段的供水、出力遭到破坏,如式(2)。
| $ \left\{ \begin{array}{l} W\left( {i, 4} \right) = \left( {Q\left( {i, 4} \right) + 2{\rm{ }}580} \right) \times t\left( {i, 4} \right)\;\;\sum\limits_{m = 1}^M {{{W'}_m}} \left( {i, 4} \right) \ge {w_{{\rm{sed}}}}\left( {i, 4} \right)\\ {\rm{s}}{\rm{.t}}{\rm{.}}\left\{ \begin{array}{l} {Q_{\rm{P}}}\left( {i, j} \right) \ge {Q_{\rm{G}}}\left( {i, j} \right)\\ {N_m}\left( {i, j} \right) \ge N_m^{\min }\left( {i, j} \right) \end{array} \right.\;\;j > 4 \end{array} \right. $ | (2) |
式中:W(i,4)为第i年第4时段梯级水库的下泄水量(m3);Q(i,4)为第i年第4时段梯级水库不考虑调沙时的下泄流量(m3/s);t(i,4)为第i年第4时段的时段长(s);W′m(i,4)为第m水库第i年第4时段初的蓄存水量(m3);wsed(i,4)为一次调沙所需水量(m3);Nm(i,j)为第m水库第i年第j时段的平均出力(MW);Nmmin(i,j)为第m水库的保证出力(MW)。
1.3.3 约束条件模型约束条件包括:水位约束、下泄流量约束、水量平衡约束,电站出力约束和变量非负约束等,防洪、防凌、生态分别在水位约束、下泄流量约束方面体现。
(1) 水位约束:
| $ Z_m^{\min }\left( {i, j} \right) \le {Z_m}\left( {i, j} \right) \le Z_m^{\max }\left( {i, j} \right) $ | (3) |
式中:Zm(i,j)为第m水库第i年第j时段末水位(m);Zmmin(i,j)为第m水库第i年第j时段的最低水位,分别对应龙羊峡水库的死水位2 530 m及刘家峡水库的死水位1 694 m;Zmmax(i,j)为第m水库第i年第j时段的最高水位,汛期(7—10月)分别对应龙羊峡水库的汛限水位2 594 m及刘家峡水库的汛限水位1 726 m,非汛期分别对应龙羊峡水库的正常蓄水位2 600 m及刘家峡水库的正常蓄水位1 735 m。
(2) 下泄流量约束:
| $ Q_m^{\min }\left( {i, j} \right) \le {Q_m}\left( {i, j} \right) \le Q_m^{\max }\left( {i, j} \right) $ | (4) |
式中:Qm(i,j)为第m水库第i年第j时段的平均下泄流量(m3/s);Qmmin(i,j)为第m水库第i年第j时段的最小下泄流量,即下游河道生态流量300 m3/s;Qmmax(i,j)为第m水库第i年第j时段的最大下泄流量,防凌期(11月至次年3月)刘家峡最大下泄流量分别为:723,480,439,383和421 m3/s;除此之外非汛期龙羊峡、刘家峡水库的最大下泄流量分别为最大过机流量1 200和1 552 m3/s。
(3) 水量平衡约束:
| $ {V_m}\left( {i, j + 1} \right) = {V_m}\left( {i, j} \right) + \left( {Q_m^{\rm{I}}\left( {i, j} \right) - {Q_m}\left( {i, j} \right)} \right) \times t\left( {i, j} \right) $ | (5) |
式中:Vm(i,j)与Vm(i,j+1)分别为第m水库第i年第j时段的时段初、末库容(m3);QmI(i,j)与Qm(i,j)分别为第m水库第i年第j时段的入库、出库流量(m3/s)。
(4) 电站出力约束:
| $ N_m^{\min }\left( {i, j} \right) \le {N_m}\left( {i, j} \right) \le N_m^{\max }\left( {i, j} \right) $ | (6) |
式中:Nm(i,j)为第m水库第i年第j时段平均出力(MW);Nmmin(i,j)为第m水库第i年第j时段的最小出力,分别对应龙羊峡水库的保证出力589.8 MW及刘家峡水库的保证出力400 MW;Nmmax(i,j)为第m水库第i年第j时段的最大出力,分别对应龙羊峡水库的装机容量1 280 MW及刘家峡水库的装机容量1 160 MW。
1.4 求解算法针对本文所建立缺水量最小模型,采用自迭代模拟优化算法[19-20]进行求解。模型变量因子为梯级水库时段出库流量,识别结构分为子系统识别与全系统识别两层,子系统识别为年调度过程中的水库水位、断面流量、时段出力3个识别项目;全系统识别为长系列调度过程的总发电量、总供水量、总调沙水量3个目标识别项目。通过两层系统识别,对变量因子进行反馈修正自迭代,最终输出运算结果。自迭代模拟优化算法的求解流程如图 1所示。

|
图 1 自迭代模拟优化算法求解流程 Figure 1 Flow chart of self-iterative optimization algorithm |
龙羊峡、刘家峡梯级水库联合运行后,龙羊峡水库为龙头水库,刘家峡转变为龙羊峡的反调节水库,起到保障防凌期防凌安全及配合龙羊峡水库兼顾梯级发电任务的作用。因此,刘家峡水库的水位过程受龙羊峡出库影响明显,本文仅从龙羊峡的水位变化过程分析水库运行情况,如图 2所示。
|
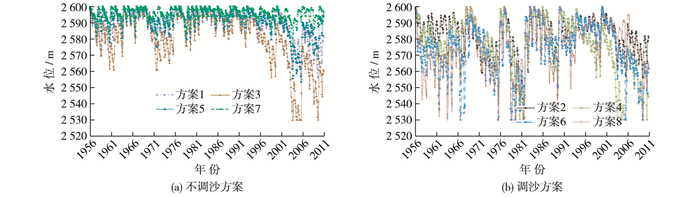
图 2 各方案龙羊峡水位变化过程 Figure 2 Water level hydrograph of Longyangxia reservior under different schemes |
由图 2可知:
(1) 从4个不调沙方案(方案1, 3, 5, 7)的龙羊峡水位变化总体趋势分析,其共性为1956—1995年这40年龙羊峡水位总体处于较高水位运行,变幅平稳,说明这40年来黄河上游径流量丰枯比例协调,特别是方案7加入了西线调水80亿m3,使得龙羊峡来水充足,实时满足多目标用水需求,因此水位变幅平稳。与此相反,各方案中1996—2010年龙羊峡水位变幅较大,水库补枯作用明显,这是由于该期间黄河上游径流呈减小趋势,且枯水年占比增大,促使水库持续动用自身库容补水,水位不断降低,表现最为明显的是方案3,水位一度降至死水位运行。
(2) 从不调沙方案的龙羊峡水位变化过程差异分析,方案3的变幅最大,方案1和5次之,方案7最小。原因是方案3为2030年无调水情景,长系列来水过程与方案1相同,但每年的需水量由方案1的238亿m3增长至263亿m3,因此水库补水量增大,水位变幅增大;方案7由于西线调水量级较大,龙羊峡水库入库流量大幅增加,无需水库过多补水,因此水位变幅最小。
(3) 从4个调沙方案(方案2,4,6,8)的龙羊峡水位变化过程分析,与不调沙相比,调沙方案的长系列水位波动剧烈,调水调沙对水位的下拉作用明显,甚至降至死水位2 530 m。此外,各调沙方案的调水调沙主要集中在1956—2000这45年中,后10年中仅方案8能调沙3次,其余方案均不能调沙。这主要是受后期天然径流减小影响,水库优先满足供水、发电用水,除方案8外,均无力再承担调水调沙水量。
2.2 综合效益分析 2.2.1 梯级水库调水调沙现状年及远景年各调沙方案的评价指标主要为:调沙力度、总调沙次数、调沙频率。反映了黄河上游梯级水库调水调沙的可行性与可持续性,详细数据见表 4。
| 表 4 调水调沙评价指标 Table 4 Evaluation indexes for water and sediment regulation |
(1) 从调沙力度分析,现状年及2030年无西线调水情景(方案2和4)的调沙力度为15 d/次,2030年西线调水40亿m3及调水80亿m3情景(方案6和8)的调沙力度为30 d/次。方案2和4不能进行30 d/次调水调沙的原因是:无西线调水的补充,方案2和4的来水过程不足以支撑多次持续时间为30 d的调水调沙。这将导致龙羊峡、刘家峡水库水位急剧下降,加之长系列过程后期来水总体偏枯,水位无法稳健回升,使得梯级水库的后续供水、发电任务遭到严重且持续的破坏,违背了调水调沙需优先满足供水、发电的基本原则。
(2) 从长系列调沙次数分析,同一调沙力度下的方案4较方案2调沙次数减少了5次,这是由于二者的来水过程一致,但方案4的需水较方案2有所增加,减少了梯级水库的可调沙水量,致使调沙次数减小。方案8较方案6的调沙次数增加了8次,说明西线调水量级的增大,将明显提高梯级水库调水调沙的能力。
(3) 总体而言,各调沙方案的调沙指标结果较为满意,反映了现状及未来一定时期内黄河上游有能力进行梯级水库调水调沙,以缓解上游宁蒙河段泥沙淤积、二级悬河的问题,且未来西线工程的运行将更有利于这一目标的实现。
2.2.2 供水效益供水效益是龙羊峡、刘家峡水库首要满足的用水目标,总体来看,现状年及远景年各方案均能满足需水要求,具体数据见表 5。
| 表 5 供水效益评价指标 Table 5 Evaluation indexes of water-supply benefit |
(1) 从多年平均供水量及缺水量分析。各方案的多年平均供水量略低于相应的需水值,缺水量最小的方案为方案1(即2010水平年不调沙方案),仅2.6亿m3/a;缺水量最大的方案为方案8(即2030水平年调沙方案),为13.3亿m3/a。各情景调沙方案较不调沙方案的缺水量有所增加,主要原因是调沙方案的长系列调沙用水挤占了部分兰州断面供水。
(2) 从供水保证率分析。不调沙方案(方案1,3,5,7)供水保证率均在85.0%以上,其中最高值为方案1的94.5%,供水保障效果良好;调沙方案(方案2,4,6,8)供水保证率为75.0%~76.4%,仅刚好达到或略微高于设计要求,这是由于考虑长系列调水调沙后梯级水库发电、供水、调沙调沙三者之间的用水矛盾较为突出,为了综合协调各目标的用水量,供水目标仅按设计保证率完成即可。
(3) 发电效益。年发电量是评价水库发挥兴利效益的一个重要指标,图 3中龙羊峡、刘家峡梯级水库的各方案年发电量变化过程反映了调沙与否与西线调水对发电效益的影响。
|
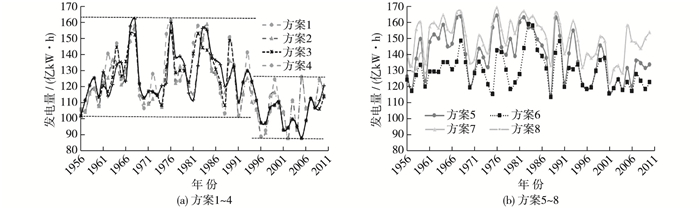
图 3 各方案龙羊峡、刘家峡梯级水库年发电量变化过程 Figure 3 Power generation of cascade reservoirs of different schemes |
由图 3可知:
(1) 图 3(a)中4个方案的年发电量曲线呈两段式分布。受天然径流减少影响,1996—2010年的梯级水库发电量较前40年总体呈下降趋势,最小值为方案2中的2002年87.9亿kW·h;方案1~4的多年平均发电量分别为122.4,119.7,120.9和120.5亿kW·h,方案1和2的梯级发电保证率为92.7%和91.0%。可见,现状条件下黄河上游进行调水调沙的同时能够满足龙羊峡、刘家峡水库发电要求,然而远景年2030无西线调水的情况下,龙羊峡、刘家峡水库的发电保证率将遭到破坏,不调沙方案的发电保证率仅为72.7%,远低于90%的设计保证率,调沙方案则进一步降低至70.9%。主要原因是受远景年供水量增加影响,加之长系列来水过程的后期天然径流减小,水资源综合利用的矛盾突出,水库后期持续动用自身库容补水,导致水头降低且无法快速回升,发电效益受损。
(2) 图 3(b)中4个方案的年发电量过程线与图 3(a)相比,未呈现明显的两段式,说明西线工程的贯通缓解了水库长系列运行中由于天然径流减少所带来的不利影响;且图 3(b)中的梯级水库年发电量总体较图 3(a)有所提高,年发电量均在110亿kW·h以上。方案5~8的多年平均发电量分别为139.3,129.4,150.0和138.6亿kW·h,梯级发电保证率分别为96.4%,96.4%,98.2%和98.2%,均能满足发电要求。其中,方案7的年发电量最高,原因是西线调水80亿m3极大地补充了黄河上游的水资源量,且此方案没有调水调沙对水库水位的集中下拉影响,能使水库保持较高水位运行,梯级发电量显著增加。
(3) 各情景下调沙方案的发电量过程总体低于不调沙方案,即龙羊峡、刘家峡水库联合调水调沙对梯级发电量将产生负面影响。受调沙力度不同影响,现状年及2030年无西线工程的调沙方案较不调沙方案梯级发电量的减少程度低于有西线工程的情况,即方案2较方案1梯级年发电量平均减少2.7亿kW·h;方案4较方案3平均减少0.3亿kW·h;方案6较方案5平均减少了9.9亿kW·h;方案8较方案7平均减少了11.5亿kW·h。这是由于方案2和4为15 d/次的调沙力度,而方案6和8为30 d/次的调沙力度,使得方案2和4中调水调沙时的梯级水库水位下降程度低于方案6和8,保留了一定的发电水头,因此调水调沙对发电量的影响较小。这也表明了在黄河上游水资源量不充裕的情况下,降低调沙力度是协调发电与调沙关系的有效手段。
3 梯级水库合理库容分析 3.1 梯级水库长系列库容规模分析由上述现状年及远景年各方案龙羊峡、刘家峡水库长系列运行过程,逐年判断龙羊峡、刘家峡水库的蓄水期和供水期,采用时历法[21]求得单个水库逐年的兴利库容。由于篇幅所限,此处仅列出2030年西线调水80亿m3(方案7和8)时龙羊峡、刘家峡水库的库容规模长系列变化过程,见图 4所示。
|
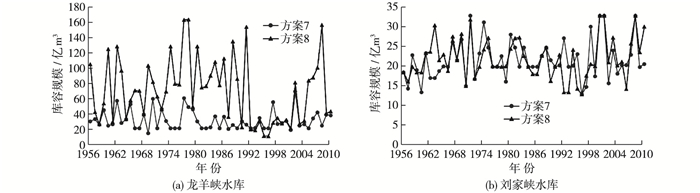
图 4 方案7和8梯级水库所需兴利库容变化过程 Figure 4 Changes in active storage of cascade reservoirs of schemes 7 and 8 |
由图 4可知:
(1) 图 4(a)为方案7和8的龙羊峡水库所需库容规模长系列变化过程。明显地,方案8(即调沙方案)的库容规模总体大于方案7(不调沙方案),方案8的库容均值为71.7亿m3,较方案732.1亿m3高出了39.6亿m3。方案7的长系列库容规模中,最大值为2002年的70.3亿m3,最小值为1969年的15.6亿m3;方案8的最大值为1978年的164.7亿m3,最小值为1996年的11.8亿m3。方案8的库容变化过程表现为调沙年份库容增大,库容规模与调水调沙呈正相关;方案7反映了丰水年组时水库缺水量小则所需兴利库容小的规律。
(2) 图 4(b)为方案7和8的刘家峡水库所需库容规模长系列变化过程,与图 4(a)不同,调沙与不调沙方案刘家峡水库的库容变化过程较为贴近。方案8的刘家峡水库库容均值为21.9亿m3,较方案7的库容均值为21.6亿m3,仅高出0.3亿m3,说明调水调沙对刘家峡水库的库容要求影响不大,主要承担调水调沙任务的水库为龙羊峡水库,刘家峡水库起配合作用。
3.2 各方案梯级水库合理库容龙羊峡水库与刘家峡水库二者的调节性能不同,确定合理库容的方法也不相同:多年调节水库取长系列径流调节过程中水库在连续枯水年组的最大累积补水量与缺水量之和为合理库容值,年调节水库取库容频率曲线中设计保证率90%对应的库容值为合理库容,结果见表 6所示。
| 表 6 各方案梯级水库合理库容 Table 6 Active storage of cascade reservoirs of each scheme |
由表 6可知:
(1) 从8个方案梯级水库兴利库容值的普遍规律分析。首先,远景年无西线工程情景(方案3和4)梯级水库所需合理库容均较现状年情景(方案1和2)增加,分析原因主要为远景年兰州断面需水增加所致。其次,各情景调沙方案的梯级水库兴利库容与不调沙相比有所增大,且龙羊峡水库的增加幅度明显比刘家峡高。这是由于长系列调水调沙增加了梯级水库的用水量,使得供水期补水量增加,所需的库容规模增大;而梯级水库调水调沙过程中,主要由龙羊峡水库承担了大部分的调沙水量,因此龙羊峡水库所增加的库容较大。
(2) 从远景年西线工程对梯级水库兴利库容的影响分析。方案3,5和7的梯级水库兴利库容分别是222.9,202.7和156.9亿m3,即远景年西线工程调水量增加将使得水库兴利库容随之减小。这是由于西线工程是一个均匀的调水过程,每月的调水量实时地用于满足水资源综合利用,调水量越大,梯级水库供水期的缺水量越小,因此所需的库容规模越小。
(3) 各方案梯级水库合理库容值与现有兴利库容值226.9亿m3相比较。各情景不调沙方案(方案1,3,5,7)的梯级水库合理库容均小于现有值,其最大值为方案3的222.9亿m3,最小值为方案7的156.9亿m3,分别较现有值减小了4.0亿m3和70.0亿m3;说明在不考虑调水调沙时,龙羊峡、刘家峡水库现有库容完全能够满足现状水平年及规划水平年的综合用水需求。但各情景调沙方案(方案2,4,6,8)中,除方案8外,其余方案的梯级水库合理库容值均超过现有库容,说明在本文所采用的调沙力度与调沙频率下,现有库容值无法完全满足现状及未来不同西线调水下的调水调沙、供水、发电等综合用水要求。
4 结语由于缺少2011年至今的黄河上游月径流过程,无法通过模拟调度分析近几年上游来水过程的变化对梯级水库供水、发电、调水调沙的影响。但通过查阅历年的《黄河水资源公报》可知:2011—2017年龙羊峡年均入库径流量为206.72亿m3,较1956—2010多年平均值增加了8.72亿m3,增幅4.41%;2011—2017年龙羊峡、刘家峡区间年均入流53.07亿m3,较1956—2010多年平均值增加了0.25亿m3,增幅0.47%;2011—2017年刘家峡至兰州区间年均入流39.72亿m3,较1956—2010多年平均值减少了3.37亿m3,降幅7.82%。总体而言,2011—2017年黄河上游梯级水库的年径流量较1956—2010多年平均值略微增大,这将有助于增加梯级水库供水、发电用水,减少缺水,降低梯级水库所需合理库容。另一方面,由于南水北调东线一期、中线一期工程已分别于2013年11月、2014年12月12日开始实施调水,有效改善了北京、天津等省市地区的缺水局面,理论上可为“八七分水”方案置换部分黄河水量,减少兰州断面需水。但是,对于“八七分水”方案的调整是一个敏感而复杂、涉及诸方利益的问题,目前政府机构尚未做出实际调整举措,故“八七分水”方案仍然是现状将继续维持的用水方案,适用于本文中现状水平年的分析计算。
黄河上游梯级水库兴利库容规模的确定是一个复杂的系统工程问题,需要综合考虑供水、发电、未来调水调沙及西线调水工程对其影响。本文基于黄河上游宁蒙河段泥沙淤积而迫切需求的水库调水调沙,及未来南水北调西线工程的实施对上游梯级水库库容规模所提出的新要求,通过建立梯级水库联合调水调沙模型及求解,分析现状年及远景年调沙与否、西线调水与否对上游梯级水库的库容规模的不同要求,探求龙羊峡、刘家峡水库所需的合理库容值,以论证上游龙羊峡、刘家峡水库现有的兴利库容能否满足未来复杂的水资源多目标利用情况。结果表明:未来2030水平年的兰州需水增加将导致龙羊峡、刘家峡水库所需合理库容增加,但西线工程的贯通与调水量级的增加将有助于降低综合用水对梯级水库库容规模的要求。若不考虑长系列调水调沙,现有的龙羊峡、刘家峡水库兴利库容能够满足现状及未来一定时期内的黄河上游综合用水;但长系列调水调沙则对现有梯级水库库容提出了挑战,仅当2030水平年西线调水80亿m3情景下现有库容能够满足调水调沙及其他综合用水要求。在此情况下,当西线调水80亿m3尚不能实现时,适当减小调沙力度或降低调沙频率不失为缓解宁蒙河段泥沙淤积与现有工程条件之间矛盾的折中选择。探求新的水资源利用形势下的梯级水库合理库容有利于科学指导黄河上游水资源利用的总体工程布局,通过梯级水库的科学调度,实现宁蒙河段河道健康与水资源兴利相协调的目标,追寻人与自然的和谐共处。
| [1] |
张营营, 胡亚朋, 张范平. 黄河上游天然径流变化特性分析[J]. 干旱区资源与环境, 2017, 31(2): 104-109. ( ZHANG Yingying, HU Yapeng, ZHANG Fanping. The characteristics of natural streamflow in the upstream of the Yellow River[J]. Journal of Arid Land Resources and Environment, 2017, 31(2): 104-109. (in Chinese)) |
| [2] |
孙洋洋, 穆兴民, 高鹏, 等. 黄河上中游区径流量格局长期变化过程[J]. 水土保持研究, 2017, 24(3): 121-127. ( SUN Yangyang, MU Xingmin, GAO Peng, et al. Temporal changes in runoff in the upper and middle reaches of Yellow River[J]. Research of Soil and Water Conservation, 2017, 24(3): 121-127. (in Chinese)) |
| [3] |
师长兴. 黄河上游内蒙古段河床演变及其与水沙变化的关系[J]. 地理科学, 2016, 36(6): 895-901. ( SHI Changxing. Channel adjustments of the inner Mongolia reach of the upper Yellow River to changes in water discharge and sediment load[J]. Scientia Geographica Sinica, 2016, 36(6): 895-901. (in Chinese)) |
| [4] |
秦毅, 李子文, 刘强, 等. 黄河内蒙段泥沙组成与力学运动特征[J]. 水利水运工程学报, 2017(3): 16-24. ( QIN Yi, LI Ziwen, LIU Qiang, et al. Sediment fraction and its mechanic movement characteristics in Inner Mongolia reach of Yellow River[J]. Hydro-Science and Engineering, 2017(3): 16-24. (in Chinese)) |
| [5] |
李秋燕, 蔡强国, 方海燕. 黄河宁蒙河段河道演变过程及影响因素研究[J]. 干旱区资源与环境, 2012, 26(2): 68-73. ( LI Qiuyan, CAI Qiangguo, FANG Haiyan. Channel evolvement and influence factors in Ningxia-Inner Mongolia reach of the Yellow River[J]. Journal of Arid Land Resources and Environment, 2012, 26(2): 68-73. (in Chinese)) |
| [6] |
罗全胜, 许新勇. 黄河内蒙河段水流数值模拟研究[J]. 水利水运工程学报, 2014(5): 95-99. ( LUO Quansheng, XU Xinyong. Flow numerical simulation for Inner Mongolia reach of the Yellow River[J]. Hydro-Science and Engineering, 2014(5): 95-99. DOI:10.3969/j.issn.1009-640X.2014.05.015 (in Chinese)) |
| [7] |
安催花, 鲁俊, 钱裕, 等. 黄河宁蒙河段冲淤时空分布特征与淤积原因[J]. 水利学报, 2018, 49(2): 195-206. ( AN Cuihua, LU Jun, QIAN Yu, et al. Spatial-temporal distribution characteristic and course of sedimentation in the Ningxia-Inner Mongolia reaches of the Yellow River[J]. Journal of Hydraulic Engineering, 2018, 49(2): 195-206. (in Chinese)) |
| [8] |
李国英. 黄河调水调沙[J]. 人民黄河, 2002(11): 1-4. ( LI Guoying. Water and sediment regulation of Yellow River[J]. Yellow River, 2002(11): 1-4. DOI:10.3969/j.issn.1000-1379.2002.11.001 (in Chinese)) |
| [9] |
胡春宏, 陈绪坚, 陈建国. 黄河水沙合理配置研究[J]. 中国科技论文, 2007(7): 463-473. ( HU Chunhong, CHENG Xujian, CHENG Jianguo. Research on the optimal allocation of water and sediment in the Yellow River[J]. China Sciencepaper, 2007(7): 463-473. (in Chinese)) |
| [10] |
张明, 张建民, 刘敏, 等. 调水调沙对黄河下游河道过水能力的影响[J]. 水资源与水工程学报, 2009(3): 140-143. ( ZHANG Ming, ZHANG Jianmin, LIU Ming, et al. Impact on discharge capacity by sediment-runoff regulation in downstream of the Yellow River[J]. Journal of Water Resources and Water Engineering, 2009(3): 140-143. (in Chinese)) |
| [11] |
纪昌明, 刘方, 彭杨, 等. 基于鲶鱼效应粒子群算法的水库水沙调度模型研究[J]. 水力发电报, 2013, 32(1): 71-76. ( JI Changming, LIU Fang, PENG Yang, et al. Study of water-sediment operation model of reservoirs with catfish-effect particle swarm optimization algorithm[J]. Journal of Hydroelectric Engineering, 2013, 32(1): 71-76. (in Chinese)) |
| [12] |
白夏, 吴成国, 黄强, 等. 黄河上游不同用水情景下可调输沙水量概念探析与估算分析[J]. 水力发电报, 2015, 34(3): 96-102. ( BAI Xia, WU Chengguo, HUANG Qiang, et al. Discussion and analysis on concept and estimation of regulatable water volumes for sediment transport in the upper Yellow in different water demand scenarios[J]. Journal of Hydroelectric Engineering, 2015, 34(3): 96-102. (in Chinese)) |
| [13] |
白涛, 阚艳彬, 畅建霞, 等. 水库群水沙调控的单-多目标调度模型及其应用[J]. 水科学进展, 2016, 27(1): 116-127. ( BAI Tao, KAN Yanbin, CHANG Jianxia, et al. Single-multi-objective operation and its application on the regulation of water and sediment by cascade reservoirs[J]. Advances in Water Science, 2016, 27(1): 116-127. (in Chinese)) |
| [14] |
姚文艺, 侯素珍, 丁赟. 龙羊峡、刘家峡水库运用对黄河上游水沙关系的调控机制[J]. 水科学进展, 2017, 28(1): 1-13. ( YAO Wenyi, HOU Suzhen, DING Yun. Effects on flow and sediment in the upper Yellow River by operation of Longyangxia Reservior and Liujiaxia Reservoir[J]. Advances in Water Science, 2017, 28(1): 1-13. (in Chinese)) |
| [15] |
姚前前, 李新举, 王梅, 等. 小浪底运行对黄河三角洲水沙变化规律的影响机制[J]. 水土保持学报, 2012, 26(6): 57-62. ( YAO Qianqian, LI Xinju, WANG Mei, et al. Influencing mechanism of the operation of Xiaolangdi project in flow/sediment variation rules in Yellow River delta[J]. Journal of Soil and Water Conservation, 2012, 26(6): 57-62. (in Chinese)) |
| [16] |
吕学军, 左登华. 南水北调西线一期工程研究[J]. 水土保持研究, 2006, 13(2): 189-192. ( LV Xuejun, ZUO Denghua. Research on the 1st-stage project of west-line for transferring water from southern to northern China[J]. Research of Soil and Water Conservation, 2006, 13(2): 189-192. DOI:10.3969/j.issn.1005-3409.2006.02.061 (in Chinese)) |
| [17] |
水利部黄河水利委员会编. 黄河流域综合规划(2012-2030年)[M]. 郑州: 黄河水利出版社, 2013: 108. ( The Yellow River Water Conservancy Commission. Comprehensive planning of the Yellow River Basin (2012-2030)[M]. Zhengzhou: The Yellow River Water Conservancy Press, 2013: 108. (in Chinese))
|
| [18] |
白涛.黄河上游沙漠宽谷河段水沙调控研究[D].西安: 西安理工大学, 2013. (BAI Tao. Research on water and sediment regulation of desert wide valley reach upper the Yellow River[D]. Xi'an: Xi'an University of Technology, 2013. (in Chinese)) http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D516080
|
| [19] |
白涛, 黄强, 陈广圣, 等. 基于水库群优化调度的黄河干流梯级补偿效益分析[J]. 西北农林科技大学学报(自然科学版), 2013, 41(5): 189-195. ( BAI Tao, HUANG Qiang, CHEN Guangshen, et al. Reservoirs optimal operation based analysis of cascade compensation benefits in main stream of the Yellow River[J]. Journal of Northwest A & F University (Natural Science Edition), 2013, 41(5): 189-195. (in Chinese)) |
| [20] |
李会安, 黄强, 沈晋. 黄河上游水库群防凌优化调度研究[J]. 水利学报, 2001(7): 51-56. ( LI Huian, HUANG Qiang, SHEN Jin. Optimal operation of cascade reservoirs in upper reaches of Yellow River for preventing ice jam[J]. Journal of Hydraulic Engineering, 2001(7): 51-56. DOI:10.3321/j.issn:0559-9350.2001.07.009 (in Chinese)) |
| [21] |
王平. 水电工程径流调节和水能计算的改进时历法[J]. 水力发电学报, 2015, 34(1): 17-22. ( WANG Ping. Improved chronological series method for calculations of runoff regulation and water power of hydroelectric projects[J]. Journal of Hydroelectric Engineering, 2015, 34(1): 17-22. (in Chinese)) |
2. State Grid Shaanxi Ankang Hydropower Station, Ankang 725000, China
 2018
2018 
