2. 三峡大学土木与建筑学院, 湖北 宜昌 443002
目前各国抗震规范中普遍采用的是“小震不坏、中震可修、大震不倒”的设计思想, 然而这种设计思想是基于强度或承载力的设计理论, 并不能准确反应混凝土大坝在强震激励下的真实性能。近几年, 国内外学者开始尝试将基于性能的抗震思想[1]用于高坝抗震分析:张社荣等[2]基于性能的抗震设计思想, 运用概率分析法, 对水工重力坝动力反应参数进行了随机描述, 得出水平地震加速度与年超越概率的近似关系式, 为概率地震反应计算提供了基础; 沈怀至等[3]提出了坝体-地基系统整体易损性曲线的评价概念, 为大坝地震风险评估与决策提供参考; Soysal等[4]基于性能设计思想建立混凝土拱坝抗震分析模型, 并分析了各影响因素与大坝损伤的关联性, 其中峰值加速度被认为是较好的整体损伤预测因子; Terzi等[5-6]也研究了基于性能的堆石坝抗震分析的一些关键问题。
随着性能设计思想的不断深入, 基于性能的结构地震响应分析方法——增量动力分析法[7](IDA法)逐渐被运用在水工建筑物抗震分析中。基于非线性动力分析的IDA方法, 可以考虑地震作用的随机性和结构体系中各种因素的影响, 能够较真实地反映在不同强度地震动作用下结构的抗震性能, 可以对结构的抗震能力做出较为全面的评价。Vanmvatsikos等[7]阐述了IDA的基本原理及其统一术语, 为IDA法从理论到实际工程运用提供了基础。针对水工结构, Aiembagheri等[8]运用IDA法以Pine Flat重力坝为例, 判断该坝在静力和动力情况下的可靠度, 并利用敏感性分析各参数指标对大坝抗震性能的重要性。Amirpour等[9]发现损伤指标中坝顶位移较上游、下游超应力区峰值应力更为合理。李静等[10]认为相比传统的拱坝抗震性能评价指标, 坝体损伤体积比和坝面损伤面积比可以更清晰地反映高拱坝抗震承载能力和损伤程度。
在以往研究中, 针对大坝抗震分析模型中坝体与库水的动力相互作用大多采用传统的附加质量法, 坝体与地基相互作用也基本上采用无质量地基法, 这些方法都在一定程度上夸大了大坝在地震作用中的响应, 并不能精确反映大坝的实际抗震能力, 因此如何建立精确高效的混凝土坝坝体-地基-库水抗震分析模型将变得尤为关键。本文基于增量动力分析法, 建立以黏弹性边界法和流固耦合法为基础的混凝土坝体-地基-库水抗震分析模型, 利用分位分析对比传统模型的结果, 对混凝土重力坝的抗震性能进行评价。
1 IDA方法 1.1 IDA方法的基本原理及步骤增量动力分析是将地震动记录分别进行系数调整, 放大到多个强度等级, 组成1组不同强度的地震动时程。这种调整只针对原地震动的幅值, 基本上保留了地震动频谱特征, 然后再利用这组调幅后的地震记录进行非线性时程分析求得结构的动力响应, 最后通过绘制IDA曲线来评估结构的性能。
基于IDA方法分析重力坝抗震性能的基本步骤[9]如下:
(1) 建立能够正确反映重力坝在地震作用下动力响应主要特征的坝体-地基-库水抗震分析模型。
(2) 选择符合该重力坝所处场地条件的1组地震记录, 并确定合适的地震动强度指标IM(intensity measure)和结构损伤指标DM(damage measure)。
(3) 选择1条时程进行非线性时程分析。
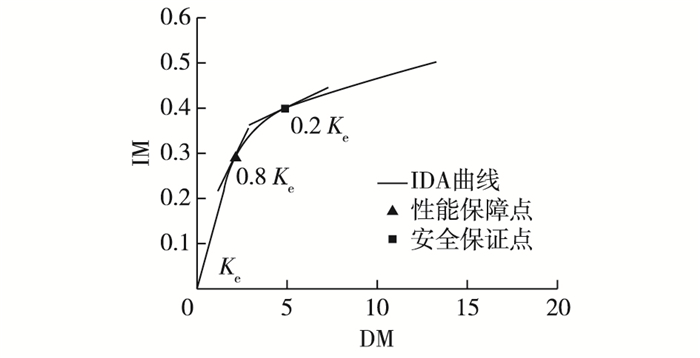
(4) 以每条地震时程所得到的地震动强度指标IM为y轴坐标和结构损伤指标DM为x轴坐标, 将时程分析结果进行插值得到相应的IDA曲线, 并在IDA曲线上定义性能保障点和安全保证点(见图 1)。
|
图 1 IDA曲线示意 Figure 1 IDA curves |
(5) 得到多条IDA曲线后, 对IDA曲线进行统计得到16%, 50%, 84%分位线和中值分位线, 并在这4条IDA曲线上定义性能保障点和安全保证点, 以此对该重力坝性能保障水平和安全水平进行分析和评价。
1.2 IDA方法的参数指标及性能目标点IM是IDA曲线中地震强度的指标。我国《水电工程防震抗震设计规范》[11](NB35057—2015)采用地面峰值加速度(PGA)作为地震动强度指标, 因此以地面峰值加速度(PGA)作为IM。
DM是IDA曲线中描述工程结构性能参数的指标。DM的选取主要由工程结构的自身特性、用途和功能决定, 而坝顶和坝址的相对位移和极限状态下的结构性能有非常好的相关性, 因此以坝顶相对位移作为DM。
我国现行水工建筑物抗震设计规范[11]和国际水工抗震规范均采用二级抗震设防水准。因此可将坝体性能水平同样划分为二级, 分别为功能保障水平和安全保证水平。根据文献[12]定义斜率为80%弹性斜率时的点为功能保障点, 定义斜率为20%弹性斜率时的点为安全保证点。
1.3 分位分析方法分位分析时, 可假定IDA曲线上每个IM-DM点服从对数正态分布[13-14], 根据IDA曲线上的某一特定IM值, 得到不同DM值的均值(m)和对数值的标准差(δDM), 继而可以得到16%, 50%, 84%分位线和中值分位线, 再根据各分位线斜率确定功能保障点和安全保证点。分别采用两种模型对Koyna大坝进行抗震分析, 为了对比分析两种模型功能保障点和安全保证点, 定义安全冗余度如下:
| $ R{\text{ = }}\frac{{{m_2}-{m_1}}}{{{m_2}}} $ | (1) |
式中:m1, m2分别为两种模型相同保证率下各功能保障点和安全保证点对应的DM值。
2 坝体-地基-库水抗震分析模型 2.1 坝体-库水数值模型 2.1.1 附加质量法我国《水电工程防震抗震设计规范》[11]针对坝体-库水相互作用采用Westergaard附加质量法考虑动水压力效应, 附加质量m′i在上游面节点i处可表示为:
| $ {m'_i} = \frac{7}{8}\sqrt {h{y_i}{\rho _{\text{w}}}} \left( {{b_{i1}} + {b_{i2}}} \right)/2 $ | (2) |
式中:h为库水深度; yi为节点到自由水面距离; ρw为库水密度; bi1和bi2为大坝上游面节点i处梁四边形单元的外边缘长度。
2.1.2 流固耦合法采用流固耦合中势流模式[15], 对于势流单元, 基于流体无旋、无黏和均质假定, 可得到以压力P为目标的波动方程:
| $ {\nabla ^2}P = P''/{c^2} $ | (3) |
式中:P″为压力对时间的二阶导数; c为流体中的声速。边界条件如下:
| $ \partial P/\partial n =-\rho {U''_n} $ | (4) |
式中:n为坝体-库水交界面的法向; U″n为法向加速度。自由液面边界, 忽略水表面力波影响时P=0。采用Galerkin法分别建立库水和坝体的动力平衡方程[15], 并组合成统一的矩阵形式:
| $ \left[{\begin{array}{*{20}{c}} \mathit{\boldsymbol{M}}&0 \\ {\rho \mathit{\boldsymbol{Q}}}&\mathit{\boldsymbol{G}} \end{array}} \right]\left( \begin{gathered} {U''} \hfill \\ {P''} \hfill \\ \end{gathered} \right) + \left[{\begin{array}{*{20}{c}} \mathit{\boldsymbol{C}}&0 \\ 0&\mathit{\boldsymbol{L}} \end{array}} \right]\left( \begin{gathered} {U'} \hfill \\ {P'} \hfill \\ \end{gathered} \right) + \left[{\begin{array}{*{20}{c}} \mathit{\boldsymbol{K}}&{-{Q^{\text{T}}}} \\ 0&\mathit{\boldsymbol{H}} \end{array}} \right]\left( \begin{gathered} U \hfill \\ P \hfill \\ \end{gathered} \right) = \left( \begin{gathered} R \hfill \\ {R'} \hfill \\ \end{gathered} \right) $ | (5) |
式中:U和P分别为位移和动水压力; M, K, C分别为结构的质量矩阵、刚度矩阵和阻尼矩阵; G, H, L分别为流体的质量矩阵、刚度矩阵和阻尼矩阵; Q为坝-库交界面上的耦合矩阵。
2.2 黏弹性边界及地震动输入方法黏弹性边界是由Deek等[16]在黏性边界基础上提出的。它的基本思想是在截断边界上并联的弹簧-阻尼器物理元件, 能够自然满足人工边界处的力平衡和位移连续条件, 具有能同时模拟散射波辐射和半无限地基的弹性恢复能力的优点, 且能克服黏性边界引起的低频漂移问题, 稳定性好。由位移连续条件和力学平衡条件, 人工边界上任一点B的动力方程[16-17]为:
| $ {m_B}{\ddot u_{Bi}}\left( t \right) + {C_B}{\dot u_{Bi}}\left( t \right) + {K_B}{u_{Bi}}\left( t \right) = F_{Bi}^{\text{f}}\left( t \right) + F_{Bi}^{\text{s}}\left( t \right) $ | (6) |
式中:KB, CB为节点B的人工边界参数; FfBi和FsBi分别为模拟边界自由场和散射场在B结点沿i方向施加的等效结点荷载。二维黏弹性边界系统的刚度系数KB和阻尼系数CB分别为:
切向边界:
| $ {K_{B{\text{T}}}} = {\alpha _{\text{T}}}\frac{{G'}}{R}, {C_{B{\text{T}}}} = \rho {C_{\text{s}}} $ | (7) |
法向边界:
| $ {K_{B{\text{N}}}} = {\alpha _{\text{N}}}\frac{{G'}}{R}, {C_{B{\text{N}}}} = \rho {C_{\text{P}}} $ | (8) |
| $ {C_{\text{p}}} = \sqrt {\frac{{\lambda + 2\mu }}{\rho }} = \sqrt {\frac{{\left( {1-\gamma } \right)E}}{{\left. {\left( {1 + \gamma } \right)\left( {1-2\gamma } \right)\rho } \right)}}} $ | (9) |
| $ {C_{\text{s}}} = \sqrt {\frac{\mu }{\rho }} = \sqrt {\frac{E}{{2\left( {1 + \gamma } \right)\rho }}} $ | (10) |
式中:E, G′, λ, μ, γ, ρ分别是地基弹性模量、剪切模量、Lame常数、泊松比和地基重度和质量密度; R为散射波源到人工边界的距离; CP和Cs分别为远域地基的纵波和横波波速[18], 参数αN和αT取1.0和0.5。
将上述各系数代入文献[18]等效节点力公式, 可得等效地震荷载, 在此不再赘述。
2.3 坝体-地基-库水抗震分析模型Koyna重力坝一直是经典的混凝土坝动力分析研究对象, 以Koyna大坝为例, 建立Koyna大坝坝体-地基-库水系统的抗震分析模型[19], 最大坝高103 m, 库水深91.75 m, 坝顶宽14.8 m, 坝底厚70 m, 选取坝基深度及库水长度约为3倍坝高, 计算模型的坝体及地基采用四节点平面应变单元。混凝土的材料参数如下:弹性模量为31.0 GPa, 泊松比为0.2, 密度为2 643 kg/m3, Rayleigh阻尼因数根据线弹性分析得到的前两阶频率计算, 阻尼比取8%;动态拉伸屈服强度σt=2.9 MPa, 抗压强度σc=24.1 MPa。
(1) 模型1(传统模型):采用附加质量法考虑坝体-库水相互作用和无质量地基法考虑坝体-地基相互作用的Koyna重力坝抗震分析模型, 节点数4 071, 单元数3 776。
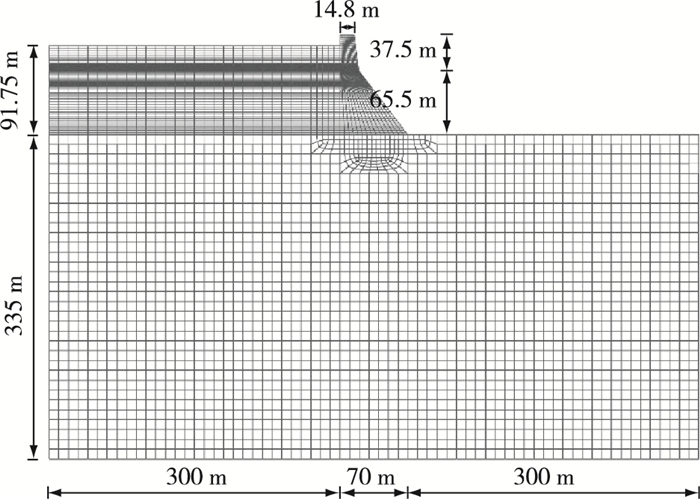
(2) 模型2:采用流固耦合法考虑坝体-库水相互作用和黏弹性边界法考虑坝体-地基相互作用的Koyna重力坝抗震分析模型, 计算模型中节点数6 070, 单元数5 728, 其中底边及侧边有黏弹性单元130个。图 2为Koyna重力坝有限元计算模型。
|
图 2 Koyna重力坝有限元计算模型 Figure 2 Finite element calculation model for Koyna dam |
据Koyna的地震地质资料[20]和《水电工程防震抗震设计规范》[11](NB 35057—2015)中标准设计反应谱, 在Pacific Earthquake Engineering Research Center(PEER)数据库中选取了15条与本工程场地特性及设计反应谱匹配较好的实测地震动记录, 另外增加了1条经典的Koyna地震记录, 选取的地震记录如表 1所示。
| 表 1 选取的地震记录 Table 1 Selected earthquake records |
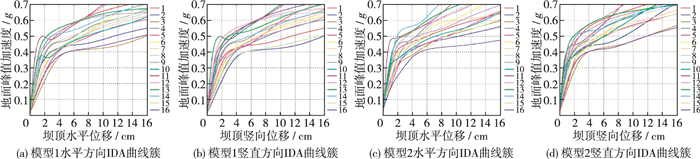
将地震记录的地面峰值加速度(PGA)分别按(0.1~1.0)g分位10级逐级调幅, 调幅上限考虑极罕遇特大地震。将调幅后地震时程导入模型1和模型2, 分别取水平向和竖直向坝顶、坝址相对位移, 模型输出结果作为DM(x轴), 并取输出结果所对应的地面峰值加速度作为IM(y轴), 将(0.1~1.0)g共10组数据插值形成IDA曲线。同理, 完成16条IDA曲线, 得到图 3所示的不同计算模型的IDA曲线。
|
图 3 两种模型的IDA曲线簇 Figure 3 IDA curves given by two models |
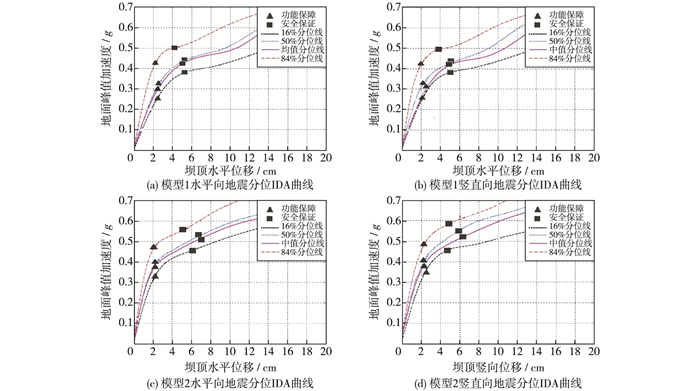
根据IDA曲线簇进行分位分析。图 4列出了不同方向地震时Koyna大坝各关键部位的16%, 50%, 中值和84%分位曲线, 各分位曲线上性能保障点和安全保证点对应的PGA见表 2。
|
图 4 两种模型的地震分位IDA曲线 Figure 4 Fractile IDA curves given by two models |
| 表 2 不同分位概率下各性能水平对应的PGA Table 2 PGA corresponding to performance levels of different fractile probabilities |
以表 2中的16%分位概率(即具有84%保证率)下运用传统方法建模的模型1各性能水平对应的PGA为例进行讨论:水平向地震时, 大坝在PGA达到2.61 m/s2(0.266g), 混凝土仍处在线弹性阶段, 大坝并未造成实质性破坏, 满足功能保障性能水平; 在PGA达到3.69 m/s2(0.376g)时, 混凝土虽存在一定损伤, 但大坝未产生不可控位移, 满足安全性能水平; 垂直流向地震时, 大坝在PGA达到2.56 m/s2(0.261g)时, 满足功能保障性能水平。在PGA达到3.64 m/s2(0.371g)时, 满足安全水平。相比传统方法建立的模型1, 运用黏弹性边界法和流固耦合方法建立的坝体-地基-库水相互作用的抗震模型, 以表 2中的16%分位概率(即具有84%保证率)下大坝的各性能水平对应的PGA为例进行讨论:水平向地震时, PGA达到3.32 m/s2(0.339g)时, 大坝仍能够满足功能保障性能水平, 相比传统方法建立的模型, 安全冗余度提高了21.5%;在PGA达到4.48 m/s2(0.451g)时, 满足安全性能水平, 相比传统方法建立的模型, 安全冗余度提高了17.7%;垂直流向地震时, 大坝在PGA达到3.36 m/s2(0.330g)时, 仍然能够满足功能保障性能水平, 相比传统方法建立的模型, 安全冗余度提高了21.0%。在PGA达到4.42 m/s2(0.451g)时, 仍然能够满足安全性能水平, 安全冗余度提高了18.5%。
同理, 针对表 2中值分位线, 模型2相比于传统模型, 其功能保障和安全保证的安全冗余度在水平向地震作用下, 分别提高了19.7%和16.5%;在竖直向地震作用, 分别提高了19.1%和19.9%。针对表 2中50%分位线(即具有50%保证率), 模型2相比于传统模型, 其功能保障和安全保证的安全冗余度:水平向地震作用下, 分别提高了19.4%和18.2%;竖直向地震作用, 分别提高了16.9%和19.0%。针对表 2中84%分位线(即具有16%保证率), 模型2相比于传统模型, 其功能保障和安全保证的安全冗余度:在水平向地震作用下, 分别提高了9.85%和13.5%;在竖直向地震作用, 分别提高了9.94%和14.2%。
根据上述结果, 针对不同保证率的PGA, 模型2的不论是性能保障水平还是安全保证水平, 其安全冗余度均高于传统模型10%~20%, 说明以传统方法建立的抗震分析模型的计算结果在一定程度上偏于保守; 根据模型2结果Koyna大坝的功能保障水平为0.34g, 极限抗震能力(84%保证率)约为0.45g, 对比文献[21-22]的结果0.40g~0.45g稍有冗余, 但极限抗震能力范围基本一致。
因此, 采用以黏弹性边界法和流固耦合法建立的大坝抗震分析模型可用于混凝土重力坝抗震设计, 增量动力分析法可拓宽高坝抗震性能研究的新思路。
4 结语基于增量动力分析法, 以黏弹性边界法和流固耦合法建立坝体-地基-库水相互作用的重力坝抗震分析模型, 评估混凝土重力坝抗震性能。以Koyna重力坝为例, 选取16条地震记录, 分别建立采用附加质量法和无质量地基法的重力坝抗震分析模型和以黏弹性边界法和流固耦合法的重力坝抗震分析模型。相对于传统模型, 利用分位分析方法, 针对不同保证率的PGA, Koyna大坝的极限抗震能力(84%保证率)约为0.45g左右, 其功能保障水平0.34g, 新模型的性能保障水平和安全保证水平的安全冗余度均高于传统模型10%~20%。说明以传统方法建立的抗震分析模型的计算结果在一定程度上偏于保守, 以黏弹性边界法考虑无限域地基辐射阻尼影响, 同时采用流固耦合方法考虑坝体-库水相互作用可以有效减小大坝的动力响应, 在水工结构抗震设计时应予以重视。
采用的增量动力分析法可作为大坝抗震性能研究的新思路, 在今后研究中还应考虑选取其他地震强度指标和损伤指标进行综合分析, 相信以此建立的重力坝抗震评估模型将更加合理准确。
| [1] |
张楚汉, 金峰, 王进廷, 等. 高混凝土坝抗震安全评价的关键问题与研究进展[J]. 水利学报, 2016, 47(3): 253-264. ( ZHANG Chuhan, JIN Feng, WANG Jingting. Key issues and developments on seismic safety evaluation of high concrete dams[J]. Journal of Hydraulic Engineering, 2016, 47(3): 253-264. (in Chinese)) |
| [2] |
张社荣, 王超, 孙博. 基于性能的重力坝随机地震反应概率特征[J]. 天津大学学报(自然科学与工程技术版), 2013, 46(7): 603-610. ( ZHANG Sherong, WANG Chao, SUN Bo. Probabilistic characteristics of the performance-based seismic response of concrete gravity dams[J]. Journal of Tianjin University (Science and Technology), 2013, 46(7): 603-610. (in Chinese)) |
| [3] |
沈怀至, 金峰, 张楚汉. 基于性能的重力坝-地基系统地震易损性分析[J]. 工程力学, 2008, 25(12): 86-91. ( SHEN Huaizhi, JIN Feng, ZHANG Chuhan. Erformance-based seismic fragility analysis of concrete gravity-foundation system[J]. Engineering Mechanics, 2008, 25(12): 86-91. (in Chinese)) |
| [4] |
SOYSAL B F, BINICI B, ARICI Y. Investigation of the relationship of seismic intensity measures and the accumulation of damage on concrete gravity dams using incremental dynamic analysis[J]. Earthquake Engineering and Structural Dynamics, 2016, 45(5): 719-737. DOI:10.1002/eqe.v45.5 |
| [5] |
TERZI N U, SELCUK M E. Nonlinear dynamic behavior of Pamukcay earthfill dam[J]. Geomechanics and Engineering, 2015, 9(1): 83-100. DOI:10.12989/gae.2015.9.1.083 |
| [6] |
TORISU S S, SATO J, TOWHATA I, et al. 1-G model tests and hollow cylindrical torsional shear experiments on seismic residual displacements of fill dams from the viewpoint of seismic performance-based design[J]. Soil Dynamics and Earthquake Engineering, 2010, 30(6): 423-437. DOI:10.1016/j.soildyn.2009.12.016 |
| [7] |
VANMVATSIKOS D. Incremental dynamic analysis[M]. Springer Berlin Heidelberg, 2015.
|
| [8] |
AIEMBAGHERI M, GHAEMIAN M. Seismic assessment of concrete gravity dams using capacity estimation and damage indexes[J]. Earthquake Engineering and Structural Dynamics, 2013, 42(1): 123-144. DOI:10.1002/eqe.v42.1 |
| [9] |
AMIRPOUR A, MIRZABOZORG H. Quantifying the qualitative limit-states using IDA approach in concrete arch dams[J]. Arabian Journal for Science and Engineering, 2014, 39(11): 7729-7740. DOI:10.1007/s13369-014-1393-z |
| [10] |
李静, 陈健云, 徐强, 等. 高拱坝抗震性能评价指标研究[J]. 水利学报, 2015, 46(1): 118-124. ( LI Jing, CHEN Jianyun, XU Qiang, et al. Study on index of seismic performance evaluation of arch dam[J]. Journal of Hydraulic Engineering, 2015, 46(1): 118-124. (in Chinese)) |
| [11] |
NB 35047—2015水电工程防震抗震设计规范[S]. (NB 35047—2015 Code for seismic design of hydraulic structures of hydropower project[S]. (in Chinese))
|
| [12] |
VAMVASTSIKOS D. Seismic performance uncertainty estimation via IDA with progress accelerogram-wise Latin hypercube sampling[J]. Journal of Structure and Engineering, 2014, 140(8): 657-670. |
| [13] |
HARIRI-ARDEBILI M A, SAOUMA V E, PORTER K A. Quantification of seismic potential failure modes in concrete dams[J]. Earthquake Engineering and Structural Dynamics, 2016, 45(6): 979-997. DOI:10.1002/eqe.v45.6 |
| [14] |
ARDEBILI M H, SAOUMA V. Collapse fragility curves for concrete dams: comprehensive study[J]. Journal of Structural Engineering, 2016, 142(10): 101-115. |
| [15] |
OMIDI O, LOTFI V. A symmetric implementation of pressure-based fluid-structure interaction for nonlinear dynamic analysis of arch dams[J]. Journal of Fluids and Structures, 2017, 69: 34-55. DOI:10.1016/j.jfluidstructs.2016.12.003 |
| [16] |
DEEK A J, RANDOLPH M. Axisymmetric time-domain transmitting boundaries[J]. Journal of Engineering Mechanics, 1994, 120(1): 25-42. DOI:10.1061/(ASCE)0733-9399(1994)120:1(25) |
| [17] |
CHEN D H, DU C B, YUAN J W, et al. An investigation into the influence of damping on the earthquake response analysis of a high arch dam[J]. Journal of Earthquake Engineering, 2012, 16(3): 329-349. DOI:10.1080/13632469.2011.638697 |
| [18] |
何建涛, 马怀发, 张伯艳, 等. 黏弹性人工边界地震动输入方法及实现[J]. 水利学报, 2010, 41(8): 960-969. ( HE Jiantao, MA Huaifa, ZHANG Boyan, et al. Method and realization of the seismic motion input of viscous-spring boundary[J]. Journal of Hydraulic Engineering, 2010, 41(8): 960-969. (in Chinese)) |
| [19] |
WANG G H, ZHANG S R, ZHOU C B, et al. Correlation between strong motion durations and damage measures of concrete gravity dams[J]. Soil Dynamics and Earthquake Engineering, 2015, 69: 148-162. DOI:10.1016/j.soildyn.2014.11.001 |
| [20] |
LEE J, FENVES G L. A plastic-damage concrete model for earthquake analysis of dams[J]. Earthquake Engineering and Structural Dynamics, 1998, 27: 937-956. DOI:10.1002/(ISSN)1096-9845 |
| [21] |
刘章军, 曾波, 周宜红, 等. 地震动过程的概率模型及在重力坝抗震可靠度分析中的应用[J]. 水利学报, 2014, 45(9): 1066-1074. ( LIU Zhangjun, ZENG Bo, ZHOU Yihong, et al. Probabilistic model of ground motion processes and seismic dynamic reliability analysis of the gravity dam[J]. Journal of Hydraulic Engineering, 2014, 45(9): 1066-1074. (in Chinese)) |
| [22] |
张社荣, 王高辉, 王超. 混凝土重力坝极限抗震能力评价方法[J]. 水力发电学报, 2013, 32(3): 168-175. ( ZHANG Sherong, WANG Gaohui, WANG Chao. Study on ultimate aseismic capacity evaluation of concrete gravity dam[J]. Journal of Hydroelectric Engineering, 2013, 32(3): 168-175. (in Chinese)) |
2. College of Civil Engineering & Architecture, China Three Gorges University, Yichang 443002, China
 2018
2018 