2. 广东省水文局,广东广州 510000;
3. 中国水利水电科学研究院,北京 100038;
4. 上海水务建设工程有限公司,上海 200072
温度历程是影响混凝土力学性能的重要因素之一[1]。实际工程中,通常采用标准养护试件的热学和力学性能参数,进行大坝混凝土抗裂性及温度应力仿真分析[2]。大量文献研究表明温度对抗压强度、弹性模量、徐变度等有显著影响,王甲春等[3]研究了实际结构混凝土温度历程下以及20和50 ℃恒温养护下混凝土早期抗压强度的发展,得出3种情况下混凝土早期强度发展历程差异较大。Kim等[4-6]对温度与混凝土力学性能(抗压强度、抗拉强度和弹性模量)的关系进行了系统研究,将混凝土分别在10,23,35,50 ℃的温度下进行养护,并在1,3,7,28 d的龄期下测试其力学性能,试验表明高温养护下试件比低温养护下的混凝土试件早期抗压强度和抗拉强度更高,但后期强度则较低,同理弹性模量也有相同规律。Zhao等[7]开展了粉煤灰混凝土在不同养护温度下的徐变性能研究,发现50 ℃养护下混凝土的水化产物更多,其对应徐变度较20 ℃养护下混凝土的徐变度大。不同温度历程下混凝土力学性能发展存在较大差异性的原因是温度影响混凝土的水化反应速率,此时应将不同的温度历程等效为标准养护状态以考虑温度的影响,文献[8]和[9]基于成熟度等效龄期理论考虑温度历程对力学性能的影响,开展了混凝土温度应力与开裂分析。
混凝土应力应变监测是保证施工质量、评估大坝安全的重要手段[10]。混凝土坝的应力监测主要采用应变计组监测应变,然后根据混凝土的徐变试验成果推算应力。目前以实测应变资料计算应力的方法主要有3种[11-13]:有效弹模法、叠加法和流动率法。有效弹模法最简单,但计算的应力没有考虑混凝土施工期等阶段的应力对后续应力的影响。叠加法以叠加原理为基础,该法又分为变形法和松弛系数法。叠加法计算精度高,是目前国内外常用的计算方法。流动率法对计算精度要求较高,目前该方法在工程上使用较少。
由于混凝土热学和力学性能的发展不仅与龄期有关,还与自身温度和温度历程有关,而现有文献将实测应变转换为应力仅考虑其与龄期的关系,并未考虑温度历程的影响,因此获得的应力历程也无法反应真实的混凝土应力状态,由此作出安全评价的准确性也无法保证。据此,本文基于等效龄期理论,考虑温度对徐变度、弹性模量的影响,基于变形法推导考虑温度历程的实测应变转换为应力公式,并结合西北地区典型混凝土坝内埋应变计组实测资料进行应力计算,对比分析考虑及不考虑温度历程的应力差异。
1 基本原理 1.1 等效龄期基本原理根据Arrhenius方程提出等效龄期[14]的表达式如下:
| $ {\tau _{\rm{e}}} = \int {\exp \left[{\frac{{{U_{\rm{h}}}}}{R}\left( {\frac{1}{{{T_0}}}-\frac{1}{T}} \right)} \right]{\rm{d}}t} $ | (1) |
式中:Uh为水化活动能(J/mol);R为气体常数,取8.315 J/(mol·K);T为混凝土温度;T0为参考温度,通常取293 K,即20 ℃。
张子明[15]等通过对已有不同温度下混凝土绝热温升资料进行回归分析,认为Uh/R与混凝土实际温度T满足如下关系:
| $ {U_{\rm{h}}}/R = 16.187{T^{1.0002}} $ | (2) |
将实测应变转换为应力在文献[11-12]中有详细报导。当采用变形法将实测应变转换为实际应力时,对于一维应力状态,有
| $ \begin{array}{l} \Delta {\sigma _n} = {E_{\rm{s}}}\left( {{{\bar \tau }_n}, {\tau _{n- 1}}} \right)\left\{ {{\varepsilon _n}\left( {{{\bar \tau }_n}} \right)- \sum\limits_{i = 0}^{n- 1} {\Delta {\sigma _i}} \left[{\frac{1}{{E\left( {{\tau _i}} \right)}} + C\left( {{{\bar \tau }_n}.{\tau _i}} \right)} \right]} \right\}\\ \;\;\;\;\;\;\;\;\;\;\;\;{E_{\rm{s}}}\left( {{{\bar \tau }_n}, {\tau _{n -1}}} \right) = \frac{{E\left( {{\tau _{n -1}}} \right)}}{{1 + C\left( {{{\bar \tau }_n}, {\tau _{n -1}}} \right)E\left( {{\tau _{n - 1}}} \right)}} \end{array} $ | (3) |
式中:Δσi为各计算时段的应力增量;εn(τn)为一维应变过程线上,t=τn时刻的应变值,该值为扣除自由体积变形的测值;E(τi)为混凝土龄期τi时刻弹性模量;C(τn, τi)是以龄期τi为加荷龄期,单位应力持续作用到τn的徐变;τn=(τn-1+τn)/2,是时段中点的龄期。
对于三维应力状态,引入泊松比矩阵[16],有
| $ \Delta {\mathit{\boldsymbol{\sigma }}_n} = {E_{\rm{s}}}\left( {{{\bar \tau }_n}, {\tau _{n- 1}}} \right)\left\{ {{\mathit{\boldsymbol{Q}}^{- 1}}{\mathit{\boldsymbol{\varepsilon }}_n}\left( {{{\bar \tau }_n}} \right)- \sum\limits_{i = 0}^{n - 1} {\Delta {\mathit{\boldsymbol{\sigma }}_i}} \left[{\frac{1}{{E\left( {{\tau _i}} \right)}} + c\left( {{{\bar \tau }_n}, {\tau _i}} \right)} \right]} \right\} $ | (4) |
式中:Δσi为t=τi时刻的三维应力增量;εn(τn)为t=τn时刻的三维应变值,该值已扣除自由体积应变;Q-1为泊松比矩阵[16]。
在τn时刻的混凝土实际应力为:
| $ {\mathit{\boldsymbol{\sigma }}_n} = \sum\limits_{i = 0}^{n-1} {\Delta {\mathit{\boldsymbol{\sigma }}_i} + \Delta {\mathit{\boldsymbol{\sigma }}_n}} $ | (5) |
由上述分析可知,混凝土的热学和力学性能与自身温度和温度历程有关,即由实测应变转换为应力的计算式(3)中的徐变度c(τn, τi)和弹性模量E(τi)需要考虑温度的影响。为此,采用1.1节的等效龄期理论将实际温度历程下的力学性能转换到参考温度历程下,从而获得考虑温度历程的徐变度和弹性模量,然后将实测应变转换应力计算式(3)中的徐变度和弹性模量替换成等效龄期的徐变度和弹性模量后再进行计算,获得考虑温度历程的实际应力。由此获得考虑温度历程的一维应变转换应力公式为:
| $ \Delta {\sigma _n} = {E_{\rm{s}}}\left( {{{\bar \tau }_{{\rm{e}}n}}, {\tau _{{\rm{e}}n- 1}}} \right)\left\{ {{\varepsilon _n}\left( {{{\bar \tau }_n}} \right)- \sum\limits_{i = 0}^{n- 1} {\Delta {\sigma _i}} \left[{\frac{1}{{E\left( {{\tau _{{\rm{e}}i}}} \right)}} + c\left( {{{\bar \tau }_{{\rm{e}}n}}, {\tau _{{\rm{e}}i}}} \right)} \right]} \right\} $ | (6) |
式中:εn(τn)为一维应变过程线上,t=τn时扣除自由体积变形后的实测应变。E(τei)为基于等效龄期的弹性模量,c(τen, τei)为以等效龄期τei为加荷龄期,单位应力持续作用到等效时间τen的徐变。
引入泊松比矩阵,考虑温度历程的三维应变转换应力计算式为:
| $ \Delta {\mathit{\boldsymbol{\sigma }}_n} = {E_{\rm{s}}}\left( {{{\bar \tau }_{{\rm{e}}n}}, {\tau _{{\rm{e}}n- 1}}} \right)\left\{ {{\mathit{\boldsymbol{Q}}^{- 1}}{\mathit{\boldsymbol{\varepsilon }}_n}\left( {{{\bar \tau }_n}} \right)- \sum\limits_{i = 0}^{n - 1} {\Delta {\mathit{\boldsymbol{\sigma }}_i}} \left[{\frac{1}{{E\left( {{\tau _{{\rm{e}}i}}} \right)}} + c\left( {{{\bar \tau }_{{\rm{e}}n}}, {\tau _{{\rm{e}}i}}} \right)} \right]} \right\} $ | (7) |
式中:εn(τn)为t=τn时扣除自由体积变形后的三维应变值。
1.2.3 考虑温度历程的实测应变转换应力计算步骤根据上述分析,将考虑温度历程的实测应变转换应力计算步骤归纳如下:
(1) 基准时刻选取。埋入混凝土中应变计的基准值应选择在仪器和混凝土开始共同工作的时刻。由混凝土的特性可知,混凝土达到终凝时开始具备足够强度,并随龄期持续增长。因此,初步确定基准时间为混凝土终凝时间。混凝土的终凝时刻与混凝土浇注时的环境温度、入仓温度和温升过程有关,通常在12~24 h左右[11]。
(2) 无应力计测值分析。由选定的基准时间和基准值,根据规范中实测资料处理方法计算无应力计的应变和温度,与此同时,分析系统误差并加以修正或删除,然后采用最小二乘法或通过无应力计测值统计模型反演热膨胀系数并分离自生体积变形。
(3) 应变计测值分析。由选定的基准时间和基准值,根据规范中实测资料处理方法计算各应力计总应变及温度,与此同时,分析系统误差并加以修正或删除,扣除自生体积变形,获得荷载应变,然后利用第一应变不变量原理或点应变平衡原理进行误差检验,最后基于弹性力学原理,计算正应变和剪切应变。
(4) 等效龄期计算。根据应变计的实测温度历程,采用式(1)和式(2)计算出对应的等效龄期和温度历程。
(5) 考虑温度历程的应力计算。将实验室标准试验下获得的混凝土徐变度和弹性模量公式中龄期,替换为等效龄期,获得考虑温度影响的徐变度及弹性模量公式,然后根据式(6)或式(7)进行考虑温度历程的应力计算。
本文采用Visual Fortran语言编写了考虑温度历程的实测应变转换应力计算程序。
2 实例分析新疆某水利枢纽工程为I等工程,工程规模为大(Ⅰ)型。该坝坝址处多年平均气温为2.7 ℃,极端最高气温40.1 ℃,极端最低气温零下49.8 ℃。以下选取埋设在该坝典型坝段632 m高程处的S3-4编号的5向应变计组为例进行应力应变分析,应变计组埋设位置的混凝土等级为R18020W4F50,混凝土配合比如表 1所示,典型五向应变计组埋设如图 1所示,应变计组采用差阻式应变计,在应变计组附近配套埋设了1支无应力计S3-4-N。
| 表 1 混凝土材料配合比 Table 1 Proportion of concrete material |

|
图 1 五向应变计组埋设 Figure 1 Embedding schematic of strain gauge group |
绘制电阻比和温度过程线,进行粗差分析后,当测值不再跳动,温度和电阻比呈现有规律的对应变化的开始时刻即基准时刻,本文选取该混凝土坝应力计算基准时刻为1.46 d。
通过无应力计测值统计模型,分离出无应力计S3-4-N自生体积变形,热膨胀系数为9.345 0×10-6 / ℃,分析表明,自生体积变形呈收缩型,195.5 d龄期时自生体积变形达到36.84 ×10-6,随后趋于稳定。
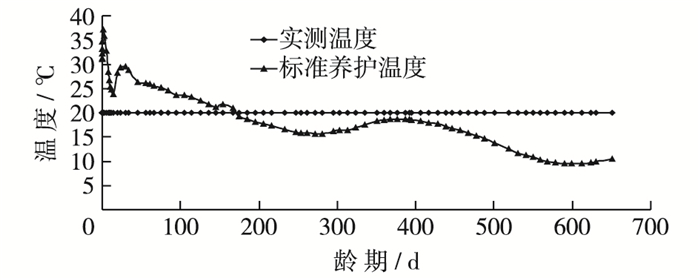
根据文献[11]中的应变计监测资料分析基本方法,获得应变计组S3-4各应变计的温度历程和总应变。S3-4处混凝土温度历程为各向应变计温度值的平均值,与标准养护温度的对比如图 2所示,由于该工程地处西北高寒地区,温控措施一般,在前160 d龄期内,混凝土内部温度均高于标准养护温度;坝体内部混凝土初期由于水泥水化热等原因,达到最高温度37.0 ℃后降温,接着新浇筑的混凝土引起温度再次回升,然后持续降温,呈现周期性的变化规律。总体来看,S3-4处混凝土温度历程的变化范围为6.4~37.0 ℃。并对五向应变计组进行误差平衡修正,然后由修正后的应变扣除自生体积变形,获得荷载应变,最后根据弹性力学原理获得正应变和剪切应变。
|
图 2 实测温度与标准养护温度对比 Figure 2 The contrast of measured temperature and the standard curing temperature |
根据式(1)~(2)计算应变计组的等效龄期,其中Uh/R取4 516.24。S3-4应变计组典型时刻2.75,142.9,26.62,45.21,60.50,94.25,280.21和500.25 d对应的等效龄期为6.06,23.90,47.46,71.17,92.32,136.30,317.60和507.42 d。可见,初期由于混凝土温度高于标准养护温度(20 ℃),混凝土等效龄期大于混凝土浇筑龄期。
根据混凝土标准试验获得混凝土的弹性模量为:
| $ E\left( \tau \right) = \frac{{34381\tau }}{{7.9216 + \tau }} $ | (8) |
混凝土的徐变度采用下式计算:
| $ \begin{array}{l} c\left( {t, \tau } \right) = \left( {0.00079 + 55.941\;48{\tau ^{-0.51678}}} \right)\left( {1-\exp \left( {-0.93595\left( {t - \tau } \right)} \right)} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\left( {0.00069 + 56.93180{\tau ^{ - 0.38715}}} \right)\left( {1 - \exp \left( { - 0.04240\left( {t - \tau } \right)} \right)} \right) \end{array} $ | (9) |
式中:τ为龄期(d);E为弹性模量(MPa);c为徐变度(10-6/MPa)。
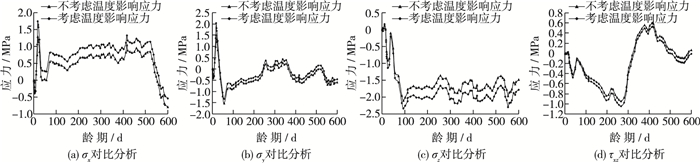
据此,由式(6)和(7)获得考虑温度历程的弹性模量、徐变度、应力,并与基于变形法计算的不考虑温度历程的应力进行对比分析如图 3所示。
|
图 3 考虑温度影响和不考虑温度影响下的应力对比分析 Figure 3 Comparison of stress with and without considering of temperature effect |
由图 3分析可见:①考虑温度历程计算的应力与不考虑温度历程计算的应力变化趋势相同。正应力和剪切应力的变化速率在两种情况下十分接近,且出现应力峰值的时刻基本相同。②考虑温度历程计算的正应力和剪切应力均大于不考虑温度历程时计算的应力。两者差值最大值分别为Δσx=0.46 MPa,Δσy=0.49 MPa,Δσz=0.31 MPa,Δτxy=0.089 MPa,不考虑温度影响时,应力最大值分别为Δσx=1.28 MPa,Δσy=1.50 MPa,Δσz=2.12 MPa,Δτxy=0.95 MPa,即最大差值分别为不考虑温度影响时应力最大值的36%,32.6%,14.6%,9.4%,且应力差值峰值出现在早期,此时由于混凝土强度未得到充分发展,若不考虑温度影响,会影响大坝安全状态的评价。
3 结语混凝土热学和力学性能的发展不仅与龄期有关,还与自身温度和温度历程有关,针对目前常用的实测应变转换应力基本方法均未考虑温度历程对力学性能发展的影响,与实际情况有较大差异,本文开展相关研究,并得到以下结论:
(1) 本文基于变形法原理,结合等效龄期理论,推导了考虑温度历程的实测应变转换应力公式,并给出了考虑温度历程将实测应变转换应力步骤。
(2) 结合西北地区典型混凝土坝五向应变计组实测资料进行应力分析,分析表明考虑温度历程计算的正应力和剪切应力均大于不考虑温度历程时计算的应力,拉应力最大差值为0.49 MPa,且应力差值峰值出现在早期,考虑到此时混凝土强度未完全发展,如果不考虑温度的影响,会影响对混凝土开裂可能性评价的准确性,进而影响结构安全。
| [1] |
梅塔P K, 蒙特罗P J M. 混凝土: 微观结构、性能与材料[M]. 覃维祖, 王栋民, 丁建彤, 译. 北京: 中国电力出版社, 2008. (MEHTA P K, MONTEIRO P J M.Concrete microstructure, properties and materials[M]. Translated by TAN Weizu, WANG Dongmin, DING Jiantong, et al. Beijing: China Electric Power Press, 2008.(in Chinese))
|
| [2] |
丁建彤, 陈波, 蔡跃波. 温度历程对早龄期混凝土抗裂性的影响[J]. 江苏大学学报(自然科学版), 2011, 32(2): 236-240. ( DING Jiantong, CHEN Bo, CAI Yuebo. Influence of temperature history on crack resistance of early age concrete[J]. Journal of Jiangsu University (Natural Science Edition), 2011, 32(2): 236-240. (in Chinese)) |
| [3] |
王甲春, 阎培渝. 温度历程对早龄期混凝土抗压强度的影响[J]. 西北农林科技大学学报(自然科学版), 2014, 42(7): 228-234. ( WANG Jiachun, YAN Peiyu. Influence of temperature history on compressive strength of early age concrete[J]. Journal of Northwest A & F University (Natural Science Edition), 2014, 42(7): 228-234. (in Chinese)) |
| [4] |
KIM J K, MOON Y H. Compressive strength development of concrete with different curing time and temperature[J]. Cement and Concrete Research, 1998, 28(12): 1761-1773. DOI:10.1016/S0008-8846(98)00164-1 |
| [5] |
KIM J K. Estimation of compressive strength by a new apparent activation energy function[J]. Cement and Concrete Research, 2003, 33(7): 965-971. DOI:10.1016/S0008-8846(03)00007-3 |
| [6] |
KIM J K. Effect of temperature and aging on the mechanical properties of concrete: Part Ⅱ. prediction model[J]. Cement and Concrete Research, 2002, 32(7): 1095-1100. DOI:10.1016/S0008-8846(02)00745-7 |
| [7] |
ZHAO Qingxin, LIU Xiaochen, JIANG Jinyang. Effect of curingtemperature on creep behavior of fly ash concrete[J]. Construction and Building Materials, 2015, 96: 326-333. DOI:10.1016/j.conbuildmat.2015.08.030 |
| [8] |
张岫文, 叶列平, 吴佩刚. 基于成熟度的大体积混凝土早期温度应力场有限元分析[J]. 建筑结构, 2005, 35(1): 68-71. ( ZHANG Xiuwen, YE Lieping, WU Peigang. Finite element analysis on thermal stress in mass concrete at early ages with maturity method[J]. Journal of Building Structure, 2005, 35(1): 68-71. (in Chinese)) |
| [9] |
金贤玉, 田野, 金南国. 混凝土早龄期性能与裂缝控制[J]. 建筑结构学报, 2010, 31(6): 204-212. ( JIN Xianyu, TIAN Ye, JIN Nanguo. Early age properties and cracking control of concrete[J]. Journal of Building Structure, 2010, 31(6): 204-212. (in Chinese)) |
| [10] |
储海宁. 关于高混凝土坝应力应变监测的几个问题——兼评安全监测规范的有关规定[J]. 大坝与安全, 2009(2): 29-37. ( CHU Haining. Several issues on stress and strain monitoring of high concrete dams-discussion on some specification in safety monitoring norm[J]. Journal of Dam and Safety, 2009(2): 29-37. (in Chinese)) |
| [11] |
储海宁. 混凝土坝内部观测技术[M]. 北京: 水利电力出版社, 1989. ( CHU Haining. Inside observation technology of concrete dam[M]. Beijing: China Electric Power Press, 1989. (in Chinese))
|
| [12] |
吴中如. 水工建筑物安全监控理论及其应用[M]. 北京: 高等教育出版社, 2003. ( WU Zhongru. Safety monitoring theory & its application of hydraulic structure[M]. Beijing: Higher Education Press, 2003. (in Chinese))
|
| [13] |
黄国兴, 惠荣炎, 王秀军. 混凝土徐变与收缩[M]. 北京: 中国电力出版社, 2011. ( HUANG Guoxing, HUI Rongyan, WANG Xiujun. The creep and shrinkage of concrete[M]. Beijing: China Electric Power Press, 2011. (in Chinese))
|
| [14] |
GEERT D S. Applicability of degree of hydration concept and maturity method for thermo-visco-elastic behaviour of early age concrete[J]. Cement and Concrete Composites, 2004, 26(5): 437-443. DOI:10.1016/S0958-9465(03)00067-2 |
| [15] |
张子明, 周红军, 殷波. 基于等效时间的混凝土徐变[J]. 河海大学学报(自然科学版), 2005, 33(2): 173-176. ( ZHANG Ziming, ZHOU Hongjun, YIN Bo. Equivalent time-based concrete creep[J]. Journal of Hohai University(Natural Science Edition), 2005, 33(2): 173-176. (in Chinese)) |
| [16] |
黄耀英, 郑宏, 周宜红, 等. 基于小概率事件法估计大坝混凝土实际抗拉强度[J]. 武汉理工大学学报, 2012, 34(3): 86-90. ( HUANG Yaoying, ZHENG Hong, ZHOU Yihong, et al. Estimation of actual tensile strength of dam concrete based on small probability event method[J]. Journal of Wuhan University of Technology, 2012, 34(3): 86-90. (in Chinese)) |
2. Guangdong Province Bureau of Hydrology, Guangzhou 510000, China;
3. China Institute of Water Resources and Hydropower Research, Beijing 100038, China;
4. Shanghai Water Construction Engineering Co., Ltd., Shanghai 200072, China
 2017
2017 
