2. 河海大学 水文水资源学院,江苏 南京 210098
近年来,对阶梯溢流坝消能工的研究表明,设计合理的阶梯式溢流坝能减小下游泄水建筑物尺寸,从而减少工程投入[1-2]。众多工程实例显示,阶梯溢流坝在高流速大流量工况下会出现消能率下降、掺气不充分易空化等问题。近几年来有学者提出将宽尾墩+阶梯溢流坝+消力池的消能方式应用于高水头大流量的泄水工程,利用宽尾墩对水流的横向收缩纵向扩展作用,加强水流充分掺气,减小了阶梯消能的压力[3],但不能避免阶梯近壁面产生空化空蚀破坏。为了解决前几级台阶因掺气导致的空化空蚀问题,朱利等提出将掺气坎布置在阶梯溢流坝闸墩出口处,通过模型试验进行研究,结果表明前置掺气坎有利于阶梯掺气,降低了阶梯面发生空化空蚀的概率;刘善君等[5]通过模型试验表明,在前置掺气坎的帮助下,阶梯溢流坝的掺气浓度有所提高并解决了过渡阶梯前几级台阶存在清水区的问题;吴守荣等[4]提出了前置掺气挑坎的体型布置,通过底部强迫掺气加强台阶面的掺气保护作用,从而有效解决了阶梯面的空化空蚀破坏问题。但就前置掺气坎角度对阶梯溢流坝坎后掺气空腔及前几级台阶上的压强影响研究较少。
胡耀华等[7-9]提出了空腔长度估算公式,但几种公式都忽略或简化了许多因素,计算结果差异较大;徐一民等[10]通过理论研究和模型试验得出空腔回水与掺气坎坎高、水流弗劳德数、空腔负压有关的结论,而在实际工程中模型试验往往受到场地及经济条件的限制,现今数值模拟凭借其扎实的理论基础、先进的模拟技术、获取资料完整和花费小等优势,已成为研究水气两相流运动的有效工具之一。笔者将掺气坎应用在Y型宽尾墩阶梯溢流坝上,通过数值模拟分析前置掺气坎角度对阶梯溢流坝上坎后掺气空腔长度及阶梯面上压力的影响。
1 物理模型及试验方案本文以某电站Y型宽尾墩+前置掺气坎+阶梯溢流坝+消力池为模拟对象,依据重力相似准则设计比尺为1 : 60的模型,采用前置掺气坎连接WES堰与阶梯溢流坝,溢流坝坝面共有29级台阶,其高度和宽度分别为1.70和1.25 cm,坝面坡脚为53°,后连接反弧段和消力池,其中反弧段半径为83.3 cm,消力池长度为235 cm。研究显示若掺气坎角度太小,则不利于水流挑射,从而导致坎后水流掺气不充分;若掺气坎角度太大,挑射水流对坝面冲击力增大,进而导致坝面破坏。工程实践表明,溢流坝中的掺气坎坡度取值范围在1:5~1:7(8°~11.3°)之间,本文为探讨前置掺气坎角度对阶梯掺气空腔长度和压力的影响,经试验研究设计前置掺气坎角度分别取8°, 10°和11.3°(掺气坎高度为1 m)。模型主要比尺如下:几何比尺为60,流量比尺为27 885,时间比尺和流速比尺均为7.75,压力比尺为60,糙率比尺为1.98。
2 数学模型采用Hirt等[11]提出适用两种互不相融流体界面跟踪计算的VOF方法,利用RNG k-ε双方程紊流模型对流场进行数值模拟,方程如下:
| $ \text{连续方程}:\;\;\;\;\;\;\;\;\;\;\partial \rho /\partial t + \partial (\rho {u_i})/(\partial {x_i}) = 0 $ | (1) |
| $ \text{动量方程}:\;\;\;\;\;\;\;\;\;\;\frac{{\partial \rho {u_i}}}{{\partial t}} + \frac{\partial }{{\partial {x_i}}}(\rho {u_i}{u_j}) = -\frac{{\partial p}}{{\partial {x_i}}} + \frac{\partial }{{\partial {x_j}}}\left[{(\mu + {\mu _{\text{t}}})\left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right)} \right] $ | (2) |
| $ k\text{方程}:\;\;\;\;\;\;\;\;\;\;\frac{{\partial \left( {\rho k} \right)}}{{\partial t}} + \frac{{\partial (\rho k{u_i})}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left[{{\alpha _k}{\mu _{{\text{eff}}}}\frac{{\partial k}}{{\partial {x_j}}}} \right] + {G_k} + \rho \varepsilon $ | (3) |
| $ \varepsilon \text{方程}:\;\;\;\;\;\;\;\;\;\;{\text{ }}\frac{{\partial \left( {\rho \varepsilon } \right)}}{{\partial t}} + \frac{{\partial (\rho \varepsilon {u_i})}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left[{{\alpha _\varepsilon }{\mu _{{\text{eff}}}}\frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right] + \frac{{C_{1\varepsilon }^{\text{*}}\varepsilon }}{k}{C_k} - {C_{2\varepsilon }}\rho \frac{{{\varepsilon ^2}}}{k} $ | (4) |
式中:xi,xj分别为坐标分量,i, j=1, 2, 3;ui为xi方向的速度瞬时分量;t为运动的时间;ρ为混合相的密度;p为修正后的压力;k为稳动能项;ε为稳动耗散率项;μ为流体动力黏度项;μt为湍流黏度项;Gk为平均梯度状况下产生的湍动能生成项,μeff=μ+μt,ak=1.0, aε=1.3(ak为k的紊流普朗特数,aε为ε的普朗特数);Cμ,C1ε和C2ε均为经验常数项,其值分别取0.09,1.44和1.92。
对第q相流体体积分数采用式(5)计算:
| $ \partial {a_q}/\partial t + {u_j}\partial {a_q}/\partial {x_j} = 0 $ | (5) |
式中:aq是第q相流体的体积分数。
在Fluent软件中,几何重建方式对水气两相流之间的交界面采用分段线性方式进行描绘,它是对水气交界面附近进行插值最精确的方法,其中几何重建方式假设水气两相流之间的界面在每个单元中均有线性斜面,并利用此线性形状的斜面为穿过单元面的流体的水平对流进行计算。
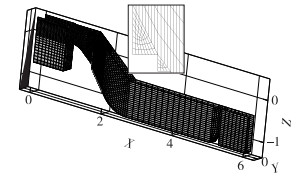
3 数值模拟域网格划分及边界条件设定 3.1 数值模拟域及其网格划分为了简化计算,取该电站5孔溢流坝中的一孔进行数值模拟。模拟区域网格结构如图 1。模拟区域原点取在溢流堰堰面曲线与上游水库交线中心位置,以水库进水方向为x轴,水库横截面方向为y轴,水库铅直方向为z轴。为使模拟结果加快收敛,数值模拟域除宽尾墩、阶梯和尾坎外都利用结构化网格进行划分,利用非结构网格宽尾墩、阶梯和尾坎处进行划分。同时网格划分的原则为密疏适当,重要部位如两相交界面的网格应相对密一些,在仅有水相或气相等次要部位区域的网格相对疏些,模拟域网格数量约为15万,台阶底部网格尺寸为0.315 cm,前置掺气坎底部网格尺寸为1.42 cm。
|
图 1 数值模拟域整体网格(单位:m) Figure 1 Whole grids of numerical simulation domain (unit: m) |
采用非结构网格和有限体积法相结合的方式对方程进行离散,压力-速度耦合采用非定常计算PISO方法,它既可以缩短计算时间又可以修正网格畸变。同时对整个计算区域进行初始化,对残差变量进行监控,采用一阶迎风格式对正在求解的动量方程进行离散,时间步长定为0.001~0.003 s。
边界条件主要划分为5种:
(1) 速度进口边界:将水库入水口边界条件设置为速度进口,单宽流量为123.66 m3/(s·m),流速为2.17 m/s。模型入口平均流速为vin=0.28 m/s。模拟区域紊动能k和耗散率ε的取值可由下列公式计算得出:
| $ k = 0.003{\text{ }}75v_{{\text{in}}}^2 $ | (6) |
| $ \varepsilon = {k^{\frac{2}{3}}}/\left( {0.4{H_0}} \right) $ | (7) |
式中:vin为进口流速;H0为进口水深。
(2) 压力进口边界:将水库入水口上方与空气联通处以及模型上方与大气连接处的边界条件设置为压力进口。
(3) 压力出口边界:将自由出流上方与空气联通处的边界条件设为压力出口。
(4) 壁面边界:模拟区域内将固壁面上的法向速度设置为零,并定义其边界条件为相对无滑移。
(5) 自由出流:将水流出水断面处的边界条件设为自由出流。
4 计算结果与分析 4.1 掺气空腔长度带有Y型宽尾墩的阶梯溢流坝通过增设前置掺气坎后,在过渡台阶处易形成稳定的水舌底部掺气空腔。通过模型试验对阶梯溢流坝阶梯面上的掺气空腔进行观测,在数值模拟中分析截面y =0的空腔形态,图 2是单宽流量为123.66 m3/(s·m)的3种方案阶梯溢流坝坎后掺气空腔形态,图中水相用红色表示,气相用蓝色表示,水气混合相用其他颜色表示,图中挑射水舌越过前几级过渡台阶,水舌底部与过渡台阶的阶梯面之间形成掺气空腔。为了验证模拟的可靠性,利用带有前置掺气坎阶梯溢流坝的三维数学模型,对已进行过物理模型试验的工况进行数值模拟计算,通过对比模拟计算值和实测值对所建立的数学模型进行验证。

|
图 2 阶梯溢流坝坎后掺气空腔形态 Figure 2 Shapes of aerated cavity behind aerator on stepped spillway |
表 1为各方案掺气空腔长度的实测值与模拟值,最大误差为7.9%(单宽流量为123.66 m3/(s·m)时)。挑角为8°时,实测值与模拟值误差为5.2%;挑角为10°时,其误差为7.9%;挑角为11.3°时,其误差为6.3%,吻合较好,其中模拟值略小于实测值,这一结果与文献[13]一致,具体原因一方面是Fluent软件无法模拟水体气泡的破碎、聚合等复杂运动,另一方面是因为不同的网格划分形式以及底部边界层定义影响模拟精度。
| 表 1 坎后掺气空腔长度实测值与模拟值 Table 1 Measured and simulated values of aerated cavity length behind aerator |
文献[10]介绍了在泄槽底坡、跌坎高度、挑坎高及下泄流量不变的情况下,掺气空腔长度随掺气坎角度的增加而增加,与本文试验结果相吻合。从表 1中可以看出在单宽流量一定时,随着前置掺气坎角度的增加,前置掺气坎对下泄水流的纵向挑射作用随之增大,挑射水舌与阶梯面之间形成的掺气空腔的覆盖范围随之增大,泄流单宽流量为123.66 m3/(s·m)时,其覆盖范围从6.05个阶梯增加到8.20个阶梯,掺气空腔长度从8.39 m逐渐增加到10.89 m。前置掺气坎角度为10°相对于前置掺气坎角度为8°时,坎后掺气空腔长度增加了7.5%,前置掺气坎角度为11.3°相对于前置掺气坎角度为10°时,坎后掺气空腔长度增加了20.7%;泄流单宽流量为92.45 m3/(s·m)时,空腔覆盖范围从5.3个阶梯增加到6.45个阶梯,掺气空腔长度从7.4 m逐渐增加到8.97 m。前置掺气坎角度为10°相对于前置掺气坎角度为8°时,坎后掺气空腔长度增加了5.8%,前置掺气坎角度为11.3°相对于前置掺气坎角度为10°时,坎后掺气空腔长度增加了14.6%,故前置掺气坎角度较大时对掺气空腔长度影响较大,反之影响较小。
由表 1还可以看出,在前置掺气坎角度一定时,随着泄流单宽流量的增大,坎后掺气空腔长度增大。前置掺气坎角度为8°时,单宽流量92.45 m3/(s·m)的掺气空腔长度为7.4 m,单宽流量123.66 m3/(s·m)的掺气空腔长度为8.39 m,增长率为13%;前置掺气坎角度为10°时,单宽流量92.45和123.66 m3/(s·m)的掺气空腔长度分别为7.83 m和9.02 m,增长率为15%;前置掺气坎角度为11.3°时,单宽流量92.45和123.66 m3/(s·m)的掺气空腔长度分别为8.97和10.89 m,增长率为21%。
坎后掺气空腔尺寸增加,空腔对泄流的通气面积增大,泄流掺气效果越好,对降低阶梯面发生空化空蚀的概率有利。由上可知,单宽流量一定时,掺气空腔长度随掺气坎角度的增加而增加,就阶梯面上坎后空腔长度而言,方案2和3优于方案1,方案5和6优于方案4。
4.2 阶梯面上平均压力沿程分布利用带有前置掺气坎的阶梯溢流坝的三维数学模型,模拟计算已进行过物理模型试验的工况,通过对坎后空腔最大负压的模拟计算值和实测值比较分析来验证本文模拟的可靠性。方案1,2,3的空腔最大负压模拟计算值依次为-3.97,-4.42和-5.20 kPa,相应实测值为-4.19,-4.57和-5.42 kPa,误差分别为5.25%,3.28%和4.06%,吻合较好,表明该模拟求解方法用来研究压力是可行的。
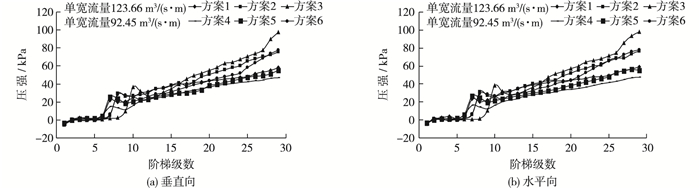
泄流单宽流量123.66和92.45 m3/(s·m)的6种方案中阶梯水平及垂直近壁面平均压力沿程分布如图 3所示,各方案中压力沿程分布形式基本一致,沿程略有波动,但总体变化趋势为沿程增大。当单宽流量一定时,相同断面处平均压力随前置掺气坎角度的增大而增大;当前置掺气坎角度一定时,相同断面处平均压力随泄流单宽流量的增大而增大。图中可以看出各方案中的压力均在掺气空腔后的阶梯上骤增,在压力值波峰所处位置后的几级台阶范围内压力值小幅度降低,随后又呈持续增长趋势,其原因为前置掺气坎将泄流挑入空中,随后泄流跌落到阶梯面后又进一步在阶梯面挑射,所以在该区间内形成压强迅速增加随后又略有减小的现象。各方案中压力最大值依次为59.23,76.32,98.16,47.23,55.32和78.16 kPa。随着冲击压力的增大,阶梯面发生破坏的概率随之增大,由上可知在其他因素一定时,方案3劣于方案1和2,方案6劣于方案4和5。
|
图 3 阶梯水平及垂直近壁面平均压力沿程分布 Figure 3 Average pressure distribution on vertical and horizontal faces of steps |
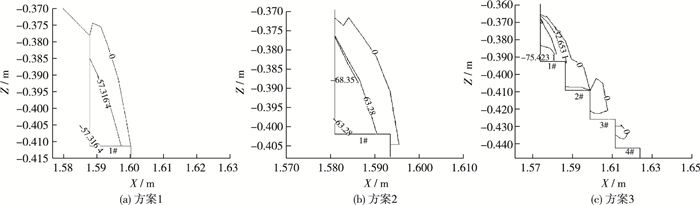
通过模拟计算发现,各方案中前几级过渡台阶上的空腔都存在局部负压,且负压大小和分布范围不同。泄流单宽流量123.66 m3/(s·m)的3种方案负压等值线分布如图 4所示,从图中可以看出当前置掺气坎挑角为8°时,前置掺气坎对水流挑射作用较小,负压分布在第1级台阶,当前置掺气坎角度为10°时,前置掺气坎对水流挑射作用增大,负压分布在第1级台阶和第2级台阶的垂直固壁面之间,当前置掺气坎角度为11.3°时,负压分布增至前四级台阶。重点分析3种方案下空腔负压的大小和分布范围,以及阶梯溢流坝阶梯水平近壁面和垂直近壁面的负压。
|
图 4 阶梯溢流坝阶梯负压等值线(单位:kPa) Figure 4 Contours of negative pressure on stepped spillway (unit: kPa) |
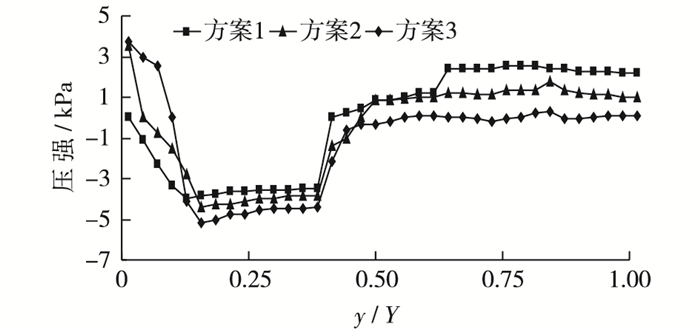
3种方案阶梯溢流坝第1级阶梯垂直近壁面负压值见表 2,方案1最大负压值为-3.97 kPa,方案2的为-4.42 kPa,方案3的为-5.20 kPa。3种方案阶梯溢流坝阶梯垂直固壁面压力分布如图 5所示,各方案负压起始值均出现在第1级台阶垂直固壁面上且产生的位置不同,依次在y/Y为0,0.036和0.072处,负压绝对值沿凸角到凹角方向,3种方案中负压绝对值先逐渐增大后略有下降。在第2级台阶上方案1不产生负压,方案2,3的负压绝对值逐渐下降,方案2负压绝对值从1.37 kPa下降到0,方案3从2.15 kPa下降到0。方案1,2在第3,4级台阶处均不产生负压,且在第3级台阶上压力小幅增加,在第4级台阶处压力小幅减小。方案3在第3级台阶处出现局部负压,负压绝对值从0.18 kPa突降到0.03 kPa,降低了83.33%,在第4级台阶处压力均在0附近,从0.27 kPa降到-0.01 kPa,随后又增加到0.12 kPa。
| 表 2 各方案阶梯水平及垂直固壁面负压值 Table 2 Negative pressure values on horizontal and vertical faceskPa |
|
图 5 3种方案中阶梯垂直近壁面压力分布 Figure 5 Pressure distribution on vertical face |
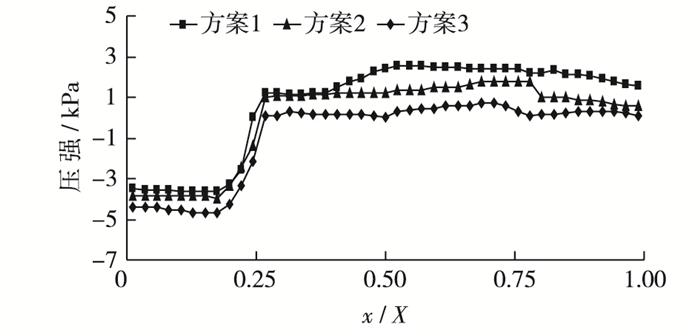
表 2为各方案阶梯溢流坝第1级阶梯水平固壁面负压值,方案1,2,3最大负压值都出现在第1级台阶上,依次为-3.61,-3.97和-4.65 kPa。3种方案阶梯溢流坝阶梯水平固壁面压力分布如图 6所示,在第1级阶梯处各方案均产生负压且负压绝对值沿x/X增大方向先逐渐增大后急剧减小,方案1,2,3负压绝对值从3.52,3.82,4.42 kPa依次上升至3.61,3.97,4.65 kPa,增长率分别为2.56%,3.93%,5.20%, 随后负压绝对值依次突降至1.24,1.40,2.15 kPa,下降率分别为65.65%,64.74%,53.76%。在第2级台阶处,方案1,2和3均不产生负压,方案1和2压力值沿台阶凹角到凸角方向逐渐增大,而方案3压力值先增后减。在第3,4级台阶上,各方案上均产生正压。
|
图 6 3种方案中阶梯水平近壁面压力分布 Figure 6 Pressure distribution on horizontal face |
由以上分析可知,掺气坎角度增大,阶梯近壁面最大负压绝对值增加且负压分布范围逐渐增大。较大的负压易引发空化空蚀破坏,故方案3与方案1,2相比较略显劣势。
5 结语通过对前置掺气坎角度分别为8°,10°和11.3°的Y型宽尾墩+阶梯溢流坝+消力池消能方式的掺气空腔长度和压力进行三维数值模拟,得出如下结论:
(1) 比较坎后空腔长度模拟值与实测值发现两者差别不大,说明本文数值模拟可行,研究结果对工程实践有一定指导作用。
(2) 在泄流单宽流量一定时,随着前置掺气坎角度增加,坎后掺气空腔的覆盖范围和长度随其增加。在前置掺气坎角度一定时,随着泄流单宽增加,坎后掺气空腔的覆盖范围和长度随其增加。
(3) 前置掺气坎角度增加,阶梯溢洪道阶梯面最大负压绝对值、负压分布范围和压力值均有所增大。方案1,2,3最大负压值依次为-3.97,-4.42和-5.20 kPa。方案2与方案1相比较,增长率为11.34%,方案3与方案2相比较,增长率为17.65%。3种方案中负压分布范围不同,方案1负压分布在第1级台阶,方案2负压分布在第1级台阶和第2级台阶的垂直固壁面之间,方案3中负压分布范围最广,几乎布满前4级台阶。方案1,2,3压力最大值分别为59.23,76.32和98.16 kPa。
由上可知,前置掺气坎角度增加,阶梯面上的掺气空腔长度随之增加,对保护阶梯面免受空化空蚀破坏有利。阶梯面上的负压绝对值和冲击压力值亦随其增大,对阶梯面减蚀和防冲不利,故在实际工程运用时应综合考虑,寻求掺气与压力的平衡,选择合理的前置掺气坎角度。
| [1] |
PEGRAM G G S, OFFICER A K, MOTTRAM S R. Hydraulics of skimming flow on modeled stepped spillways[J]. Journal of Hydraulic Engineering, 1999, 125(5): 500-510. DOI:10.1061/(ASCE)0733-9429(1999)125:5(500) |
| [2] |
CHEN Qun, DAI Guangqing, LIU Haowu. Numerical simulation for the stepped spillway overflow with turbulence model[J]. Journal of Hydrodynamics: Ser B, 2002, 14(2): 58-63. |
| [3] |
胡耀华, 伍超, 卢红, 等. 宽尾墩后接阶梯溢流坝面水工设施的研究[J]. 水力发电学报, 2006, 25(5): 37-41. ( HU Yaohua, WU Chao, LU Hong, et al. Study on hydraulic structure of flaring gate piers located at the upstream of stepped spillway[J]. Journal of Hydroelectric Engineering, 2006, 25(5): 37-41. (in Chinese)) |
| [4] |
朱利, 张法星, 刘善均. 前置掺气坎高度对阶梯溢流坝水力特性的影响[J]. 人民黄河, 2014, 36(6): 110-112. ( ZHU Li, ZHANG Faxing, LIU Shanjun. Experimental investigation on the influence of height variations of the pre-aerator upon the hydraulic characteristics of the flow in the stepped spillways[J]. Yellow River, 2014, 36(6): 110-112. (in Chinese)) |
| [5] |
刘善均, 朱利, 张法星, 等. 前置掺气坎阶梯溢洪道近壁掺气特性[J]. 水科学进展, 2014, 25(3): 401-406. ( LIU Shanjun, ZHU Li, ZHANG Faxing, et al. Aeration characteristics for skimming flow along the pre-aerator stepped spillways[J]. Advances in Water Science, 2014, 25(3): 401-406. (in Chinese)) |
| [6] |
吴守荣, 张建民, 许唯临, 等. 前置掺气坎式阶梯溢洪道体型布置优化试验研究[J]. 四川大学学报(工程科学版), 2008, 40(3): 37-42. ( WU Shourong, ZHANG Jianmin, XU Weilin, et al. Experimental investigation on hydraulic characteristics of the flow in the pre-aerator stepped spillways[J]. Journal of Sichuan University(Engineering Science Edition), 2008, 40(3): 37-42. (in Chinese)) |
| [7] |
胡耀华, 伍超, 张挺, 等. X型宽尾墩阶梯掺气空腔影响因素分析[J]. 四川大学学报(工程科学版), 2007, 39(3): 24-28. ( HU Yaohua, WU Chao, ZHANG Ting, et al. Affect factors analysis of aerated cavity of X-shaped flaring gate pier[J]. Journal of Sichuan University(Engineering Science Edition), 2007, 39(3): 24-28. (in Chinese)) |
| [8] |
杨永森, 陈长植, 于琪洋. 掺气槽上射流挟气量的数学模型[J]. 水利学报, 1996, 27(3): 13-21. ( YANG Yongsen, CHEN Changzhi, YU Qiyang. A mathematical model for self-aeration capacity of free jet on the aerator[J]. Journal of Hydraulic Engineering, 1996, 27(3): 13-21. (in Chinese)) |
| [9] |
CHANSON H. Predicting the filling of ventilated cavities behind spillway aerators[J]. J Hydraul Res, 1995, 33(3): 361-372. DOI:10.1080/00221689509498577 |
| [10] |
徐一民, 赵伟, 杨红宣, 等. 掺气挑坎、水流佛氏数及坎后空腔负压对空腔积水的影响[J]. 水力发电学报, 2010, 29(2): 15-20. ( XU Yimin, ZHAO Wei, YANG Hongxuan, et al. Influences of ramp size, Froude number and bottom cavity pressure on the cavity backwater of an aerator[J]. Journal of Hydroelectric Engineering, 2010, 29(2): 15-20. (in Chinese)) |
| [11] |
HIRT C W, NICHOLS B D. Volume of fluid (VOF) method for the dynamics of free boundaries[J]. Journal of Computational Physics, 1981(39): 201-225. |
| [12] |
张洛, 后小霞, 杨具瑞. 边宽尾墩体型对边墙区域水流水力特性的影响研究[J]. 水力发电学报, 2015, 34(1): 85-92. ( ZHANG Luo, HOU Xiaoxia, YANG Jurui. A study of impact of flaring gate pier shape on hydraulic characteristics of flow in sidewall region[J]. Journal of Hydroelectric Engineering, 2015, 34(1): 85-92. (in Chinese)) |
| [13] |
高学平, 贾来飞, 宋慧芳, 等. 溢洪道掺气坎槽后掺气水流三维数值模拟研究[J]. 水力发电学报, 2014, 33(2): 90-96. ( GAO Xueping, JIA Laifei, SONG Huifang, et al. Three dimensional numerical simulation of aerated flow downstream of aeration slot on spillway[J]. Journal of Hydroelectric Engineering, 2014, 33(2): 90-96. (in Chinese)) |
2. College of Hydrology and Water Resources, Hohai University, Nanjing 210098, China
 2017
2017 
