桩基础作为一种古老的基础形式被沿用至今,是基础工程的主要形式之一。在高桩码头、海洋平台、大跨度的跨海大桥等工程中得到了广泛应用。桩不但承受上部结构的自重,且承受着风荷载、波浪力以及土体侧向位移等水平荷载作用。目前工程中主要以中短桩为主,随着国际贸易的逐年增加,海洋平台、码头不断向着深水化、国际化的方向发展,则要求基桩从中短桩向中长桩、超长桩发展。超长桩现在理论上还没有明确的定义,但很多情况下总长L接近或超过50 m及长径比L/D≥40 [1]的桩即可作为超长桩进行分析。
目前很多学者对水平受荷桩进行了研究也提出了一些计算理论。归纳起来主要有Winkler弹性地基梁法、整体数值法和弹性理论法等[2]。其中弹性地基梁法应用最为广泛,该方法可分为弹性地基反力法和p-y曲线法[3]。弹性地基反力法又可细分为常数法、K法、C法和m法。常数法是由我国学者张有龄提出的,故也称张氏法。该法由于数学处理简单,曾在日本、美国等国家流行,但该法的假定与工程实际脱离较大,在工程应用中已逐渐被淘汰;我国公路交通部门在1974年通过一些试桩试验反算出反力系数随深度的0.5次方增加,即C法。m法假定地表处的地基反力系数为零,且该系数沿桩身方向呈线性增加趋势。
弹性地基反力法不能反映土体的非线性,仅在小位移和小荷载的情况下得到较好的效果,而对于大位移和大荷载的工况,或土体较弱的情况下,往往会产生较大误差。所以对于土体产生较大位移的情况,采用p-y曲线法求解较为合理。在对水平受荷桩的计算上,人们更为关心的是桩身的最大位移和最大弯矩。
规范推荐的p-y曲线法是以原状土的不排水抗剪强度Cu和三轴试验最大主应力差一半时的应变ε50为基本参数,但这两个参数获取难度大;而本文基于改进p-y曲线法中采用固结快剪指标近似计算不同深度处的不排水抗剪强度Cu;ε50参考Matlock法、统一法提出的参数值和前面计算得到的Cu确定,这样大大降低了所需土体参数的获取难度。本文根据Winkler地基模型构造方程组,利用桩土间相互作用力的平衡条件和位移协调条件,建立桩土共同作用方程,求解桩身各点的水平位移yi。结合桩身位移yi求解桩身弯矩,编制相应的Matlab计算程序,最后将本文计算结果与现场试验进行对比,验证本文方法的有效性。
地层结构对各类岩土工程的受力、变形、稳定性和经济性有着重要的影响[14]。同一桩基工程中选择不同的地层结构,对桩身弯矩、位移的影响是不同的。本文主要针对黏土层,且构制不同的地层结构,分析得出对桩基承载性状最有利的地层结构。
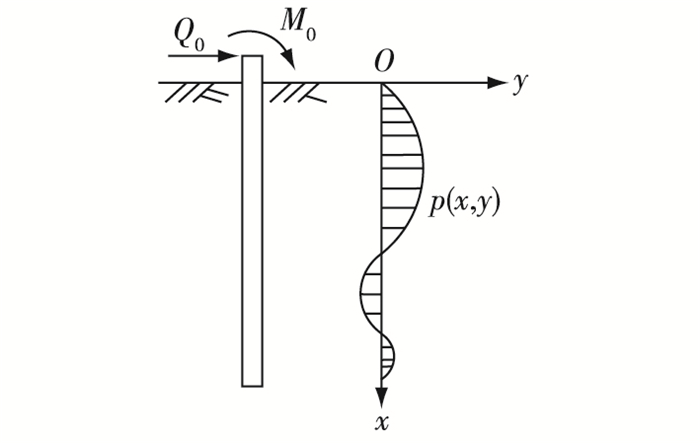
1 计算方法分析 1.1 p-y法介绍建立如图 1所示坐标系:坐标原点O定于桩轴线与土表面的交接点, 地表平面为y轴,沿桩身深度方向为x轴。
|
图 1 竖直弹性地基梁示意 Figure 1 Schematic diagram of vertical elastic foundation beam |
假设土体产生的土反力为p ,桩的横向抗弯刚度为EI, 则可导出桩身位移的基本微分方程:
| $ \frac{{\rm{d}}}{{{\rm{d}}{x^2}}}\left( {EI\frac{{{{\rm{d}}^2}y}}{{{\rm{d}}{x^2}}}} \right) + p = 0 $ | (1) |
桩顶受到水平荷载作用,随着荷载的增加桩侧土体由弹性变形过渡到塑性变形,在弹性区域可以采用弹性地基反力法;在塑性区域采用极限地基反力法。根据弹性变形与塑性变形边界上的连续条件求解桩身的水平抗力,p-y曲线法是目前应用最为广泛的方法。p-y曲线法之所以能够得到广泛的应用是因为其既适用于桩身小变形,又适用于桩身大变形的情况;且适用于任意尺寸、刚度和嵌固状态的桩。规范推荐的p-y曲线法中,由于原状土的不排水抗剪强度Cu、三轴试验最大主应力差一半时的应变ε50两个参数的获取较困难且费用高,难以在实际工程中推广。鲁子爱、周天乔等提出一种新型p-y曲线法弥补了以上不足[9]。
1.2 修改后p-y曲线法海洋工程软黏土中水平受荷桩的p-y曲线公式[9]:
| $ p = 0.8{\left( {\frac{y}{{{y_{50}}}}} \right)^{\frac{1}{8}}}{p_{\rm{u}}},p \le {p_{\rm{u}}} $ |
| $ {p_{\rm{u}}} = 1.2{C_{\rm{u}}} + 0.5\sum {\gamma h} + \frac{{0.4{C_{\rm{u}}}z}}{B},p \le 9{p_{\rm{u}}} $ |
| $ {C_{\rm{u}}} = c + 0.4\sum {\gamma h\tan \varphi } ,{C_{\rm{u}}} \le 96{\rm{kPa}} $ |
| $ {y_{50}} = 0.3{\varepsilon _{50}}B $ |
当Cu ≤18 kPa时,ε50=0.02;当18 kPa≤ Cu ≤96 kPa时,ε50=0.02[1-0.25Cu-180.25]。
在水平荷载作用下桩身的横向位移通过求解基本微分方程(1)获得。考虑到桩承受水平力和弯矩作用时,影响桩和土体受力、变形的因素很多,特别是把土体作为弹塑性变形体来考虑时,常常需要采用能利用计算机进行求解的数值分析方法,如有限差分法、有限元法等。本文采用差分法进行求解。
1.3 有限差分法有限差分法的基本原理是将桩身离散为若干个单元(假定桩身是等截面的),对各个节点以差分式近似代替桩身弹性微分方程中的导数式。对于刚度EI为常数的桩,将整个桩身沿长度方向离散为n个等分段,每个单元长度为h。在分界点i处, 设桩身的水平位移为yi、截面弯矩为Mi、土反力pi、剪力为Qi,并记该点处p-y曲线的割线模量为Esi。
假定f(x)为连续函数,各单元的长度为h, 则在i点处:
| $ {\left( {\frac{{{\rm{d}}y}}{{{\rm{d}}x}}} \right)_i} = \mathop {\lim }\limits_{{\mathit{\Delta }} x \to 0} {\left( {\frac{{{\mathit{\Delta }} y}}{{{\mathit{\Delta }} x}}} \right)_i} = \mathop {\lim }\limits_{{\mathit{\Delta }} x \to 0} \frac{{{y_{i + 1}} - {y_i}}}{{{x_{i + 1}} - {x_i}}} = \mathop {\lim }\limits_{h \to 0} \frac{{{y_{i + 1}} - {y_i}}}{h} $ |
其中:Δx=h;Δy=yi+1-yi。当h很小时,则导数
| $ \frac{{{\rm{d}}y}}{{{\rm{d}}x}}\left| {_i} \right. \approx \frac{1}{h}\left( {{y_{i + 1}} - {y_i}} \right) $ | (2) |
通常称式(2)为一阶向前差分式, 同理可以写出一阶向后差分式:
| $ \frac{{{\rm{d}}y}}{{{\rm{d}}x}}\left| {_i} \right. \approx \frac{1}{h}\left( {{y_i} - {y_{i - 1}}} \right) $ | (3) |
同理还可以写出以i为中心的一阶中心差分式:
| $ {\left( {\frac{{{\rm{d}}y}}{{{\rm{d}}x}}} \right)_i} = \mathop {\lim }\limits_{{\mathit{\Delta }} x \to 0} {\left( {\frac{{{\mathit{\Delta }} y}}{{{\mathit{\Delta }} x}}} \right)_i} = \mathop {\lim }\limits_{{\mathit{\Delta }} x \to 0} \frac{{{y_{i + 1}} - {y_{i - 1}}}}{{{x_{i + 1}} - {x_{i - 1}}}} = \mathop {\lim }\limits_{h \to 0} \frac{{{y_{i + 1}} - {y_{i - 1}}}}{{2h}} $ |
其中:Δx=2h;Δy=yi+1-yi,当h很小时,则导数dy/dx近似等于Δy/Δx,即(dy/dx)i=(Δy/Δx)i,所以有:
| $ \frac{{{\rm{d}}y}}{{{\rm{d}}x}}\left| {_i} \right. \approx \frac{1}{{2h}}\left( {{y_{i + 1}} - {y_{i - 1}}} \right) $ | (4) |
由微分性质得:
| $ \frac{{{{\rm{d}}^2}y}}{{{\rm{d}}{x^2}}} = \frac{{\rm{d}}}{{{\rm{d}}x}}\left( {\frac{{{\rm{d}}y}}{{{\rm{d}}x}}} \right) \approx \frac{{{{\mathit{\Delta }} ^2}y}}{{{\mathit{\Delta }} {x^2}}} $ |
这里用Δ2表示二次差分,则i点处的二阶中心差分:
| $ {\left( {{{\mathit{\Delta }} ^2}y} \right)_i} = {\mathit{\Delta }} \left( {{y_i} - {y_{i - 1}}} \right) = {\mathit{\Delta }} {y_i} - {\mathit{\Delta }} {y_{i - 1}} = \left( {{y_{i + 1}} - {y_i}} \right) - \left( {{y_i} - {y_{i - 1}}} \right) = {y_{i + 1}} - 2{y_i} + {y_{i - 1}} $ |
当h很小时,
| $ \frac{{{{\rm{d}}^2}y}}{{{\rm{d}}{x^2}}}\left| {_i} \right. = \mathop {\lim }\limits_{{\mathit{\Delta }} x \to 0} {\left( {\frac{{{{\mathit{\Delta }} ^2}y}}{{{\mathit{\Delta }} {x^2}}}} \right)_i} = \mathop {\lim }\limits_{h \to 0} \left( {\frac{{{{\mathit{\Delta }} ^2}y}}{{{h^2}}}} \right) = \frac{{{y_{i + 1}} - 2{y_i} + {y_{i - 1}}}}{{{h^2}}} $ | (5) |
三阶中心差分:
| $ {\left( {{{\mathit{\Delta }} ^3}y} \right)_i} = {\mathit{\Delta }} \left( {{{\mathit{\Delta }} ^2}y} \right)i = {\mathit{\Delta }} {y_{i + 1}} - 2{\mathit{\Delta }} {y_i} + {\mathit{\Delta }} {y_{i - 1}} = \frac{1}{2}\left( {{y_{i + 2}} - 2{y_{i + 1}} + 2{y_{i - 1}} - {y_{i - 2}}} \right) $ |
四阶中心差分:
| $ {\left( {{{\mathit{\Delta }} ^4}y} \right)_i} = {{\mathit{\Delta }} ^2}\left( {{{\mathit{\Delta }} ^2}y} \right)i = {{\mathit{\Delta }} ^2}\left( {{y_{i + 1}} - 2{y_i} + {y_{i - 1}}} \right) = {y_{i + 2}} - 4{y_{i + 1}} + 6{y_i} - 4{y_{i - 1}} + {y_{i - 2}} $ |
当h很小时,
| $ \frac{{{{\rm{d}}^4}y}}{{{\rm{d}}{x^4}}}\left| {_i} \right. = \mathop {\lim }\limits_{{\mathit{\Delta }} x \to 0} {\left( {\frac{{{{\mathit{\Delta }} ^4}y}}{{{\mathit{\Delta }} {x^4}}}} \right)_i} \approx \mathop {\lim }\limits_{y \to 0} {\left( {\frac{{{{\mathit{\Delta }} ^4}y}}{{{h^4}}}} \right)_i} = \frac{{{y_{i + 2}} - 4{y_{i + 1}} + 6{y_i} - 4{y_{i - 1}} + {y_{i - 2}}}}{{{h^4}}} $ | (6) |
综上得到中心差分式如下:
| $ \frac{{{\rm{d}}y}}{{{\rm{d}}x}}\left| {_i} \right. = \frac{1}{{2h}}\left( {{y_{i + 1}} - {y_{i - 1}}} \right) $ | (7) |
| $ \frac{{{{\rm{d}}^2}y}}{{{\rm{d}}{x^2}}}\left| {_i} \right. = \frac{1}{{{h^2}}}\left( {{y_{i + 1}} - 2{y_i} + {y_{i - 1}}} \right) $ | (8) |
| $ \frac{{{{\rm{d}}^4}y}}{{{\rm{d}}{x^4}}}\left| {_i} \right. = \frac{1}{{{h^4}}}\left( {{y_{i + 2}} - 4{y_{i + 1}} + 6{y_i} - 4{y_{i - 1}} + {y_{i - 2}}} \right) $ | (9) |
对于桩体刚度为常数的桩的微分方程(1)可写成下式:
| $ EI\frac{{{{\rm{d}}^4}y}}{{{\rm{d}}{x^4}}} + {E_{\rm{s}}}y = 0 $ | (10) |
将式(9)代入式(10)得
| $ EI\frac{1}{{{h^4}}}\left( {{y_{i + 2}} - 4{y_{i + 1}} + 6{y_i} - 4{y_{i - 1}} + {y_{i - 2}}} \right) + {E_{{\rm{s}}i}}y = 0 $ | (11) |
稍加整理得到i点处的差分方程为:
| $ {y_{i + 2}} - 4{y_{i + 1}} + \left( {6 + {h^4}\frac{{{E_{{\rm{s}}i}}}}{{EI}}} \right){y_i} - 4{y_{i - 1}} + {y_{i - 2}} = 0 $ | (12) |
对每个分界点i (i=0, 1, 2, 3, …,n)都能列出式(12)的方程,整个桩身被分成n段,共有n+1个分界点,即有n+1个方程,但有n+5个未知位移yi,还需补充4个方程,才能确定唯一的一组解,这4个方程需要由边界条件确定。
在桩顶i=0的受力情况明确,弯矩M0, 剪力Q0已知,以此作为桩顶的边界条件,根据微分关系可以求得两个补充方程:
| $ {y_{ - 1}} - 2{y_0} + {y_1} = \frac{{{h^2}}}{{EI}}{M_0} $ | (13) |
| $ - {y_{ - 2}} + 2{y_{ - 1}} - 2{y_1} + {y_2} = \frac{{2{h^3}}}{{EI}}{Q_0} $ | (14) |
桩底的边界条件很难确定,根据实际情况近似的假设桩底的弯矩Mn,剪力为Qn或者假设桩底的位移yd,转角y′d, 作为桩底的边界条件。
以桩底的弯矩Mn和桩底的剪力Qn作为边界条件时,补充方程如下:
| $ {y_{n - 1}} - 2{y_n} + {y_{n + 1}} = \frac{{{h^2}}}{{EI}}{M_{\rm{n}}} $ | (15) |
| $ - {y_{n - 2}} + 2{y_{n - 1}} - 2{y_{n + 1}} + {y_{n + 2}} = \frac{{2{h^3}}}{{EI}}{Q_{\rm{n}}} $ | (16) |
以桩的水平位移yd和转角y′d作为桩底的边界条件时,补充方程如下:
| $ {y_{n - 2}} - 4{y_{n - 1}} - 4{y_{n + 1}} + {y_{n + 2}} = - \left( {6 + {h^4}\frac{{{E_{{\rm{s}}n}}}}{{EI}}} \right){y_{\rm{d}}} $ | (17) |
| $ {y_{n - 1}} - {y_{n + 1}} = 2h{{y'}_{\rm{d}}} $ | (18) |
联立方程(12)~(16)或者(12)~(14),(17)~(18)得线性方程组,求出桩身各点的位移yi。
1.4 Matlab编程求解思路:(1) 假定1组Esi是p-y的切线模量,由于p-y曲线未知,所以一开始根据p-y曲线还是无法定出Esi;
(2) 根据构造的方程组求解桩身的水平位移yi;
(3) 由p-y曲线求得桩的水平位移yi所对应土抗力p值,再由Esi=pi/yi,求得1组新的Esi;
(4) 重复步骤(2),(3)直至前后两次迭代求得的y值在允许的误差范围内为止;
(5) 确定yi值后,转角、弯矩、剪力可按下式计算。
| $ {\theta _i} = \left( {{y_{i + 1}} - {y_{i - 1}}} \right)/\left( {2h} \right) $ | (19) |
| $ {M_i} = EI\left( {{y_{i - 1}} - 2{y_i} + {y_{i + 1}}} \right)/{h^2} $ | (20) |
| $ {Q_i} = EI\left( { - {y_{i - 2}} + 2{y_{i - 1}} - {y_{i + 1}} + {y_{i + 2}}} \right)/{h^3} $ | (21) |
通常情况下,实际工程中人们对桩身弯矩大小关注较多,桩身弯矩的计算式如下:
| $ \mathit{\boldsymbol{M}} = \frac{{EI}}{{{h^2}}}\left[ {\begin{array}{*{20}{c}} 0&1&{ - 2}&1&0&0& \cdots &0\\ 0&0&1&{ - 2}&1&0& \cdots &0\\ {}&{}& \ddots &{}&{}&{}&{}&{}\\ \vdots &{}&{}& \ddots &{}&{}&{}& \vdots \\ {}&{}&{}&{}& \ddots &{}&{}&{}\\ {}&{}&{}&{}&{}& \ddots &{}&{}\\ 0& \cdots &0&1&{ - 2}&1&0&0\\ 0& \cdots &0&0&1&{ - 2}&1&0 \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{y_{ - 2}}}\\ {{y_{ - 1}}}\\ {{y_0}}\\ {{y_1}}\\ \vdots \\ {{y_{n - 1}}}\\ {{y_n}}\\ {{y_{n + 1}}}\\ {{y_{n + 2}}} \end{array}} \right\} $ | (22) |
以往工程中人们通常将土体看成弹性体,例如文献[11]采用弹性地基反力法,但该方法不能反映出土体的非线性,对于港口、海洋等软弱土体适应性较差。p-y曲线法,考虑了土体的非线性,较为符合桩土相互作用的实际情况,可适应于桩身发生较大变形、海洋软土地基等情况[11-12];鉴于规范中使用的p-y曲线法获取原状土三轴试验中不排水抗剪强度Cu和三轴试验中最大主应力差一半时的应变ε50较为困难,而改进的p-y曲线中不需要通过试验来测得这两个参数,大大减小了所需土体参数的获取难度,降低了工程成本;本文编写的Matlab程序可以根据不同工况,进行灵活调整,而且编写的Matlab程序计算精度高、速度快;提高了该方法的实用性。
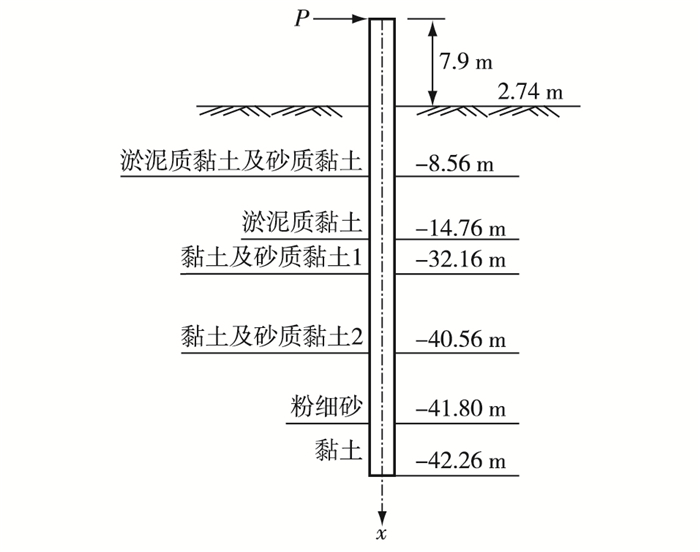
2 算例验证根据南京水利科学研究院和河海大学于1982年在镇江大港进行的水平受荷桩短期静载试验[13],测试桩采用钢管桩,测试桩的桩径1 200 mm,桩的壁厚19 mm,泥面以上自由长度为7.9 m,泥面以下桩长45 m,桩身的抗弯刚度为2.936×106 kN· m2,加载点距离泥面7.9 m。水平受荷桩示意见图 2,试验土体参数见表 1。
|
图 2 水平受荷桩示意 Figure 2 Schematic diagram of horizontal load pile |
| 表 1 试验土体各土层参数 Table 1 Parameters of each layer of experiment soil |
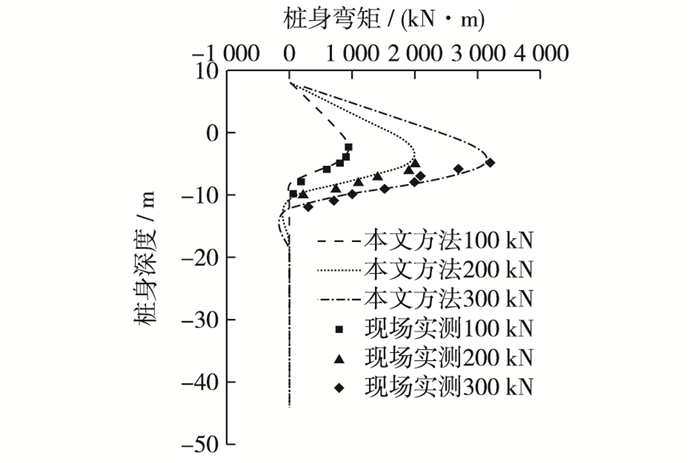
在静载单桩试验中分别在桩顶施加100,200,300 kN的水平力,桩身位移和弯矩的计算结果如图 3和4。

|
图 3 桩身水平位移对比 Figure 3 Comparison of pile horizontal displacement |
|
图 4 桩身弯矩对比 Figure 4 Comparison of pile bending moment |
位移和弯矩的计算结果都与试验数据吻合较好,验证了本文方法的正确性。该方法不但可以满足实际工程对精确度的要求,还减小了所需土体参数的获取难度,大大方便了在工程中的推广和应用。
3 工程算例某工程的桩基础,桩长48 m,埋深40 m,桩径1.2 m,桩身弹性模量3.25×104 MPa。桩周土体参数见表 2。在桩顶上作用有水平集中力F=300 kN。考虑到实际近海工程及水上桥梁工程中的桩基础往往受到冲於、人工处理等作用,导致桩基周地层结构发生变化。现基于本文推导的方法,分析水平作用力影响深度范围内的不同地层结构对桩基水平承载力的影响。
| 表 2 某工程各土层参数 Table 2 Parameters of each layer of soil in one project |
为将地层结构表述清楚,对土层进行编号从上到下分别用①②③④⑤表示。因为施加300 kN的水平力,对上面3层土的影响最为明显。以下通过改变水平力影响深度范围内的地层结构比较桩身位移和弯矩的变化。工况1地层结构为:①②③④⑤(稍硬土层在底层,软弱土层在首层,此为正常地层结构);工况2地层结构为:①③②④⑤(稍硬土层在中间,两个软弱土层夹稍硬土层);工况3地层结构为:③②①④⑤(稍硬土层在顶层,软弱土层在底层,经过工程处理后地层结构)。
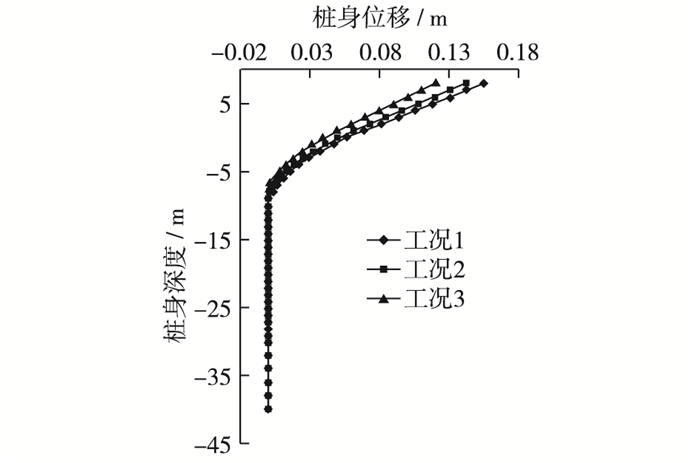
由图 5和6可以看出不同地层结构对桩身位移和弯矩有较大的影响。当由工况1变到工况2时,桩顶位移减小了8.2%,桩身最大弯矩减小了1.4%;当由工况1变化到工况3时,桩顶位移减小了22.3%,桩身最大弯矩减小了12.6%。由此可知地层结构对桩身弯矩、位移具有一定的影响。且最软弱土层在首层时(即工况1),桩身位移、弯矩都最大。当首层土体经处理之后(即工况3),桩身位移和弯矩都明显减小。
|
图 5 某工程桩身水平位移对比 Figure 5 Comparison of pile horizontal displacement |

|
图 6 某工程桩身弯矩对比 Figure 6 Comparison of pile bending moment |
(1) 本文把桩假定为弯曲杆件,结合弹性地基梁理论,运用Matlab编写相应程序,与大型有限元软件相比,具有计算速度快、易于调整等优点。通过与现场试验数据的对比,验证了本文方法的正确性与可行性。
(2) 土体参数获取的难易程度决定了方法的认可程度,本文方法中采用易于获得的土体黏聚力c近似计算出p-y曲线中所需的原状土不排水抗剪强度Cu,根据计算所得的Cu确定最大主应力差一半时的应变ε50,降低了工程成本,提高了该法在工程应用中的认可度。
(3) 本文基于改进p-y曲线法的求解程序简单易懂、经济实用,且能较好地考虑不同地基分层、土体参数变化、桩长变化等情况下部分入土单桩的水平荷载性状,具有较强的适应性。
(4) 计算复杂水平荷载作用下部分入土单桩在软黏土中的桩身位移和弯矩时,应考虑土体的塑性。
(5) 在水平力影响深度范围内对桩身位移、弯矩的最不利地层结构是从上到下由软到硬;最有利的地层结构是从上到下由硬到软。结果表明实际工程中对首层土体进行处理很重要。
| [1] |
姚文娟, 吴怀睿, 程泽坤, 等. 基于p-y曲线法的超长桩非线性数值分析[J]. 岩土工程学报, 2011, 33(11): 1683-1690. ( YAO Wenjuan, WU Huairui, CHENG Zekun, et al. Nonlinear numerical analysis of super-long piles based on p-y curves[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(11): 1683-1690. (in Chinese)) |
| [2] |
王国粹, 杨敏. 黏土中水平受荷桩基计算方法[J]. 同济大学学报(自然科学版), 2012, 40(3): 373-378. ( WANG Guocui, YANG Min. Calculation of laterally loaded piles in clay[J]. Journal of Tongji University(Natural Science), 2012, 40(3): 373-378. (in Chinese)) |
| [3] |
尹杰, 黎相森, 罗慧明, 等. 基于P-Y曲线法的单桩水平承载力计算[J]. 广东造船, 2016, 35(1): 34-36. ( YIN Jie, LI Xiangsen, LUO Huiming, et al. Calculation of single pile lateral load capacity based on P-Y curves[J]. Guangdong Shipbuilding, 2016, 35(1): 34-36. (in Chinese)) |
| [4] |
MCCLELLAND B, JR FOCHT J A. Soil modulus for laterally loaded piles[J]. Journal of the Soil Mechanics and Foundations Division, 1958, 82: 1-22. |
| [5] |
MATLOCK H. Correlation for design of laterally loaded piles in soft clay[C]//Offshore Technology Conference, Houston, Texas, 1970: 77-94.
|
| [6] |
REESE L C, COX W R, KOOP F D. Analysis of laterally loaded piles in sand[C]//Offshore Technology Conference, Houston, Texas, 1974: 95-105.
|
| [7] |
REESE L C, COX W R, KOOP F D. Field testing and analysis of laterally loaded piles om stiff clay[C]//Offshore Technology Conference, 5-8 May, Houston, Texas, 1975.
|
| [8] |
史佩栋. 桩基工程手册[M]. 北京: 人民交通出版社, 2008. ( SHI Peidong. Pile and pile foundation handbook[M]. Beijing: China Communications Press, 2008. (in Chinese))
|
| [9] |
周天乔, 鲁子爱, 王德虎. 横向受载超长PHC管桩计算方法[J]. 水运工程, 2013(6): 155-160. ( ZHOU Tianqiao, LU Ziai, WANG Dehu. Calculation method of laterally loaded super-long PHC pile[J]. Port and Waterway Engineering, 2013(6): 155-160. (in Chinese)) |
| [10] |
蒋建平, 陈文杰. 复杂水平荷载作用下部分埋入单桩的计算方法[J]. 水运工程, 2016(7): 116-121. ( JIANG Jianping, CHEN Wenjie. Calculation method for partially embedded single pile under complex horizontal loading[J]. Port and Waterway Engineering, 2016(7): 116-121. (in Chinese)) |
| [11] |
王成华, 孙冬梅. 横向受荷桩的p-y曲线研究与应用述评[J]. 中国港湾建设, 2005(2): 1-4. ( WANG Chenghua, SUN Dongmei. Review of the researches and applications of p-y curves for laterally loaded piles[J]. China Harbour Engineering, 2005(2): 1-4. (in Chinese)) |
| [12] |
刘红军, 上官士青, 王虎. 水平受荷桩p-y曲线法的数学规划法求解[J]. 工程力学, 2014, 31(4): 225-231. ( LIU Hongjun, SHANGGUAN Shiqing, WANG Hu. An optimization algorithm solution of the p-y curve method for laterally loaded piles[J]. Engineering Mechanics, 2014, 31(4): 225-231. (in Chinese)) |
| [13] |
王惠初, 鲁子爱. P-Y曲线法在镇江大港横向受载桩中的应用[J]. 河海大学学报, 1986, 14(1): 124-131. ( WANG Huichu, LU Ziai. Application of P-Y curve method to laterally loaded piles in Zhenjiang port[J]. Journal of Hohai University, 1986, 14(1): 124-131. (in Chinese)) |
| [14] |
蒋建平. 岩土工程地层结构效应与层组参数[M]. 北京: 人民交通出版社, 2011. ( JIANG Jianping. Stratigraphic structure effect and stratigraphic parameters in geotechnical engineering[M]. Beijing: China Communications Press, 2011. (in Chinese))
|
 2017
2017 