降雨条件下滑坡渗流模拟是其稳定性评价的基础,具有重要意义。对于土质滑坡,目前可采用有限元法求解Richards方程[1]来获取滑坡非饱和渗流过程,其中关键问题之一是降雨入渗边界的处理。典型的强降雨入渗过程可概述为:降雨初期,由于坡表土体含水量低,入渗能力大于雨强,雨水全部入渗;随着降雨的进行,坡表含水量逐渐增大而入渗能力逐步减小,坡表最终饱和;坡表饱和后,雨水不能全部入渗而产流。
现有数值模拟方法中,在坡表饱和之前,降雨入渗边界的处理方式大致相同,即将其视为流量边界,流量大小等于雨强;而坡表饱和之后,处理方式可分为两类。第1类方法忽略坡面径流,将降雨入渗边界视为水头边界,水头值等于地面高程[2-6];第2类方法考虑坡面径流,如采用运动波方程描述坡面径流。后者根据求解方式的不同,又可细分为2种方法:一种是采用迭代方法求解坡体渗流、坡面径流两场,其思路是先假定一个交换流量再分别求解两场,然后根据计算结果重新确定新的交换流量并分别作为两场边界,以边坡表面水深相等为依据进行迭代计算直到交换流量达到稳定值[7-12],这种方法可称之为迭代求解模型;另一种是将坡面看作渗流和径流两场的内部区域,从而避免求解交换流量,将渗流和径流两场统一求解,这种方法可称为联合求解或整体求解模型[13-15]。
文献[16]详细讨论了径流对入渗的影响,指出上述方法在考虑径流流量补给对滑体渗流影响时存在一定不足(后文将这种影响称为径流补给),并提出了一种简化的二维有限元模拟方法弥补该不足。然而,产汇流受地形影响较大,特别是三维地形,而二维模型无法真实反映该过程。因此,在文献[16]基本思想的基础上开展进一步研究,提出了考虑径流补给的滑坡降雨入渗三维数值模拟方法。
1 基本理论采用Richards方程描述滑体非饱和渗流。借助运动波方程确定径流对滑体入渗的补给流量。下面介绍相关基本理论。
1.1 Richards方程及其有限元格式Richards[1]将Darcy定律推广应用到非饱和渗流,开创了非饱和渗流的研究。水相流所满足的控制方程随之建立起来,即Richards方程:
| $ C\frac{{\partial H}}{{\partial t}} = \frac{\partial }{{\partial x}}\left( {{K_x}\frac{{\partial H}}{{\partial x}}} \right) + \frac{\partial }{{\partial y}}\left( {{K_y}\frac{{\partial H}}{{\partial y}}} \right) + \frac{\partial }{{\partial z}}\left( {{K_z}\frac{{\partial H}}{{\partial z}}} \right) $ | (1) |
式中:
初始条件为:H(x, y, z, 0)=H0(x, y, z)。简便起见,只考虑降雨入渗边界S:
未饱和时:
饱和时:H=z
其中:nx,ny,nz分别为降雨入渗边界内法线方向;R为降雨强度[L/T]。
采用Galerkin加权余量法,可建立Richards方程的有限元格式:
| $ \mathit{\boldsymbol{DH}}+\mathit{\boldsymbol{S}}\frac{\partial \mathit{\boldsymbol{H}}}{\partial \mathit{\boldsymbol{t}}}=\mathit{\boldsymbol{P}} $ | (2) |
式中:D,S,P由相应单元矩阵De,Se,Pe集成而得。各单元矩阵的元素分别为:dij=
由于运动波理论在大多数情况下可以很好地描述坡面流运动过程,且计算简单,因此仍采用运动波方程进行近似模拟[17-18],其二维格式为:
| $ \left\{ \begin{matrix} \frac{\partial h}{\partial t}+\frac{\partial {{q}_{x}}}{\partial x}+\frac{\partial {{q}_{y}}}{\partial x}+{{q}_{e}} \\ {{q}_{x}}=\frac{1}{n}{{h}^{\frac{5}{3}}}\frac{S_{x}^{1/2}}{{{(1+{{({{S}_{y}}/{{S}_{x}})}^{2}})}^{1/4}}} \\ {{q}_{y}}=\frac{1}{n}{{h}^{\frac{5}{3}}}\frac{S_{y}^{1/2}}{{{(1+{{({{S}_{x}}/{{S}_{y}})}^{2}})}^{1/4}}} \\ \end{matrix} \right. $ | (3) |
式中:qx,qy分别为x,y方向的单宽流量[L2];h为水深[L];qe为垂直净降雨强度[L/T];Sx,Sy分别为x,y方向的坡度;n为Manning糙率[T L-1/3]。
2 新数值模拟方法的构建 2.1 分析模型的简化通常情况下,滑坡渗流计算域应取自分水岭至滑坡前缘包括滑体、滑带以及滑床等区域。当滑床和滑带渗透性较小时,降雨对滑床和滑带渗流场影响很小;同时滑床和滑带与滑体间流量交换也将很小。故渗流计算域只取滑体即可。这样处理不但可减小计算规模和便于三维建模,而且也可避免因滑体与滑床(滑带)渗透系数相差过大带来数值求解上的困难。
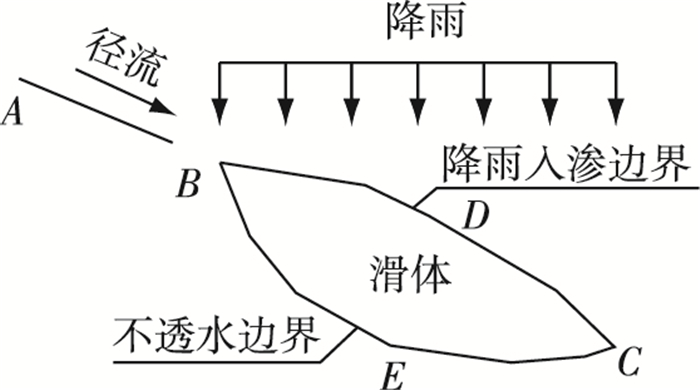
2.2 径流补给量的确定经简化后,计算边界如图 1所示(以剖面示意),其中BDC为降雨入渗边界,BEC为不透水边界。
|
图 1 渗流边界剖面 Figure 1 Diagram of profile for seepage simulation |
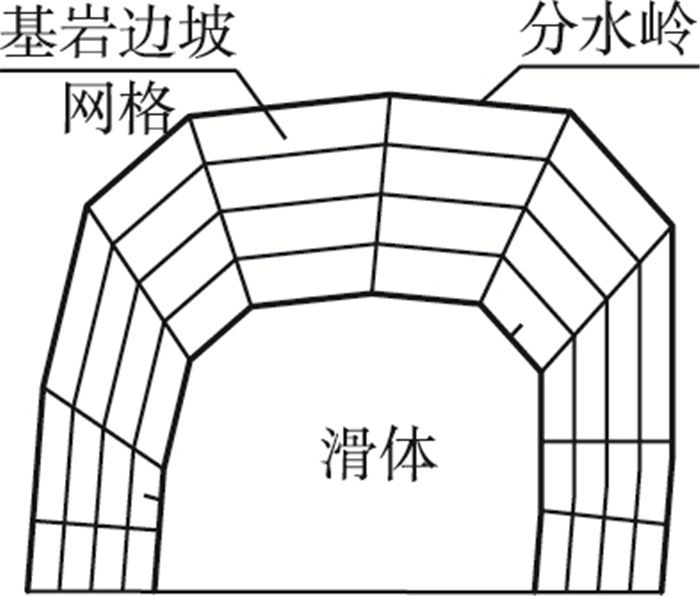
进行滑体渗流数值模拟之前,将自分水岭起至滑体边界终的滑床表面进行网格划分,如图 2所示的四边形曲面网格。
|
图 2 径流补给区网格(水平投影) Figure 2 Plane meshs of runoff |
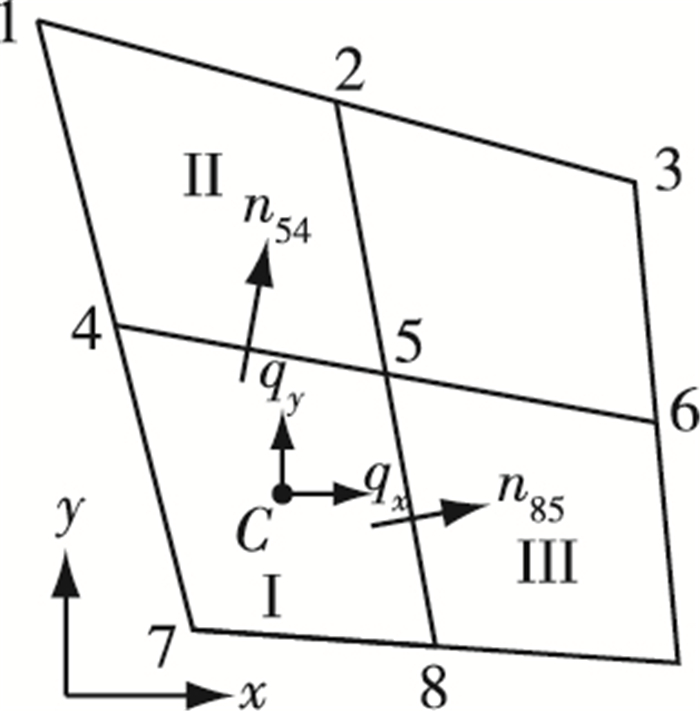
所建新方法不考虑径流过程,只考虑径流流量的传递。由于忽略滑床渗透性,降雨至其中任意一个四边形单元后,将受地形影响向周围单元径流,直至进入滑体。如图 3所示,假设单位雨强单位时间内,单元Ⅰ有降雨量QR=A[L3]向单元Ⅱ补给QⅡ[L3]和向单元Ⅲ补给QⅢ[L3],其中A为单元Ⅰ水平投影面积[L2]。则QⅡ和QⅢ确定方法如下:
|
图 3 降雨水量补给量确定 Figure 3 Precipitation supplement of one element |
设单元Ⅰ内x,y方向的单宽流量为qx[L2]和qy[L2],边85和边54的长度分别为L85[L]和L54[L],外法线方向用向量表示为n85:(n85x, n85y)和n54:(n54x, n54y),则,
| $ {{Q}_{\rm{Ⅱ}}}=({{q}_{x}}n_{85}^{x}+{{q}_{y}}n_{85}^{y}){{L}_{85}} $ | (4(a)) |
| $ {{Q}_{\rm{Ⅲ}}}=({{q}_{x}}n_{54}^{x}+{{q}_{y}}n_{54}^{y}){{L}_{54}} $ | (4(b)) |
| $ A={{Q}_{\rm{Ⅱ}}}+{{Q}_{\rm{Ⅲ}}} $ | (5) |
根据式(3),qx/qy=sx/sy, 写为
| $ q_x=(qs_x, 0), q_y=(0, qs_y) $ | (6) |
式中:sx,sy分别为单元形心处的x,y方向坡度。如果qx·n85 < 0,则表示Ⅲ向Ⅰ补给,反之则表示Ⅰ向Ⅲ补给。为方便,这里假定Ⅰ向Ⅱ和Ⅲ补给。将式(6) 代入式(4) 并结合式(5) 可得:
| $ q=A/[({{s}_{x}}n_{85}^{x}+{{s}_{y}}n_{85}^{y}){{L}_{85}}+({{s}_{x}}n_{54}^{x}+{{s}_{y}}n_{54}^{y}){{L}_{54}}] $ |
将q代回式(4),可得单元Ⅰ向单元Ⅱ和Ⅲ的补给量。若单元Ⅰ通过1条、3条或4条边向周边补给,其补给量可类似得到。
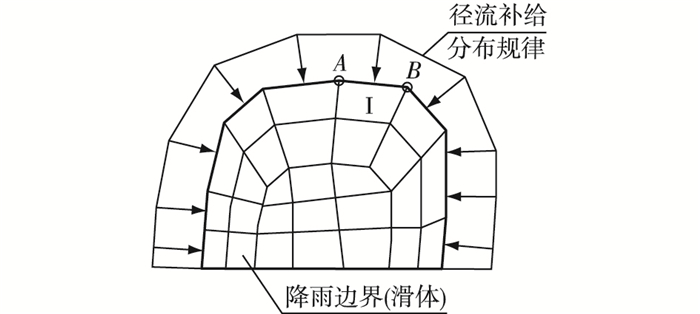
当所有单元向周围补给量确定后,可以形成树(数据结构的一种)。每个单元看做节点,父节点为向其补给的单元;子节点为受其补给的单元;补给量随同存储。可将该树先转为二叉树,然后确定每个节点向滑体的补给路径和补给量,进而确定滑体边界上受到的径流补给分布,如图 4所示。关于二叉树路径遍历问题是常见算法,此处不再叙述。
|
图 4 基岩径流补给分布平面 Figure 4 Runoff supply distribution on slide mass boundary |
在三维渗流分析中,计算域被剖分为八节点六面体网格,采用等参单元;降雨边界被剖分为四边形网格。根据2.2节方法确定径流补给在滑体边界上的分布规律后,即可对降雨边界流量进行修正。如图 4中的单元Ⅰ,给定雨强后,除降雨流量外,该单元边界流量还有来自AB边的径流补给量。
计算过程中,滑体降雨边界中的四边形也可能出现饱和情况(即4个节点水深均大于0)。此时,将该单元4个节点视为水头边界,如水头值等于地表高程;同时按照2.2节方法,确定该单元向周边单元的流量补给,该单元所能提供的补给量等于其他饱和单元对其的径流补给量加上该单元降雨量减去该单元入渗量。入渗量由所求渗流场通过式(2) 反算节点流量确定。
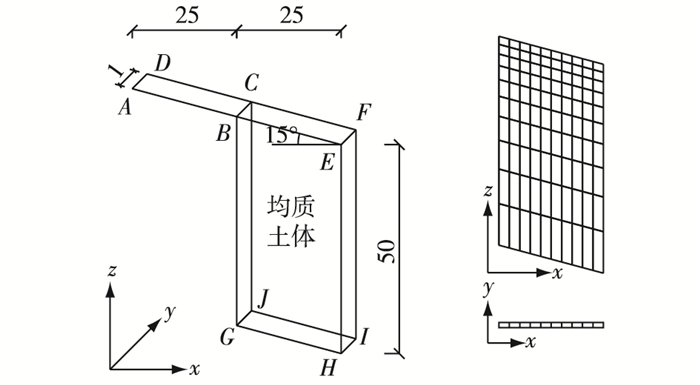
3 数值算例本算例通过模拟所得的入渗总量和渗流场来说明考虑径流补给的必要性。如图 5所示,六面体BEFCGHIJ为计算域,可代表滑体区域;ABCD为径流补给区域,可代表滑床表面;所建有限元网格节点数242,单元数100。BEFC为降雨边界,持续10 h,ABCD有相同降雨;其他为不透水边界。初始体积含水率0.1。表 1为土体的土水特征曲线及渗透性函数数据。
|
图 5 算例的几何尺寸及网格(单位:cm) Figure 5 Geometry sizes and meshes of an example (unit: cm) |
| 表 1 土体SWCC与渗透性函数 Table 1 SWCC and permeability function of soil mass |
降雨量与时间关系用Rc(t)表示:
| $ R_c(t)=50Rt $ | (7(a)) |
入渗总量与时间关系用QM1或QM2表示,分别由下式计算:
| $ {{Q}_{M1}}(t)=\sum\limits_{i=1}^{n}{\int_{ei}{({{Q}_{M1}}(t)-{{\theta }_{0}})\rm{d}\mathit{V}}} $ | (7(b)) |
| $ {{Q}_{M2}}(t)=\sum\limits_{i=1}^{n}{\int_{ei}{({{Q}_{M2}}(t)-{{\theta }_{0}})\rm{d}\mathit{V}}} $ | (7(c)) |
式中:n为单元总数,下标M1表示所建新方法计算结果,即考虑径流补给;M2表示第1类方法计算结果,即不考虑径流补给;采用高斯积分计算。
曲线D1和D2代表两种方法所得入渗总量与降雨量之差的百分比,分别由下式计算:
| $ {{D}_{1}}(t)=[{{Q}_{\rm{M1}}}(t)-{{Q}_{R}}(t)]\times 100/Q_R(t) $ | (7(d)) |
| $ {{D}_{2}}(t)=[{{Q}_{\rm{M1}}}(t)-{{Q}_{R}}(t)]\times 100/Q_R(t) $ | (7(e)) |
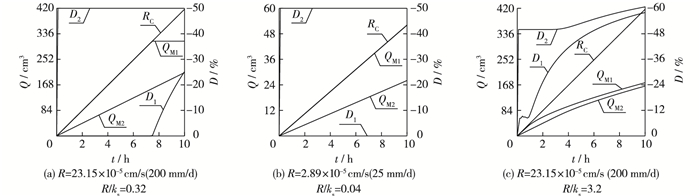
模拟时采用的雨强R和饱和渗透系数ks见表 2。图 6给出了由式(4)~(7) 计算所得的曲线,图中雨强后括号中的数字表示换算成mm/d后的大小,如R=2.89×10-5 cm/s等于R=25 mm/d。图 6(a)表示刚开始降雨量(包括ABCD段的降雨)全部渗入BCFE段,降雨量和入渗量之差几乎为0。7.5 h后,边坡完全饱和,ABCD段边坡的径流无法渗入滑体,对应总入渗量为311.3 cm3,与边坡BCFE总孔隙体积(25×50×0.25×1=312.5 cm3)几乎相同,表明计算结果正确;此后因降雨量随时间增大而入渗量保持为常量,故降雨量和入渗量之差开始增大。图 6(b)所示当边坡未饱和时,径流补给全部渗入BCFE段边坡;若不考虑径流补给,则所得入渗量与降雨量差1倍。
| 表 2 雨强和饱和渗透系数 Table 2 Values of R and ks |
|
图 6 各统计曲线 Figure 6 Statistical curves |
当ks=7.22×10-5 cm/s时,由于此时土体渗透性小,而雨强相对较大(如23.15×10-5 cm/s)时,则两种方法区别不大,如图 6(c)所示。因为即便有径流补给,但土体入渗能力有限,坡表很快饱和,再多雨水也无法入渗。
图 7为10 h时刻两种方法所得压力水头等值线对比。可见,考虑流量补给后,土体基质吸力降低更多,径流对入渗补给效果明显,意味着土体强度降低更多。特别是当雨强较大时(图 7(b)),若考虑径流补给则边坡早在7.5 h时就已完全饱和。当雨强相对渗透系数较大时,则两种方法区别不大(图 7(c)),原因同前。

|
图 7 压力水头等值线对比(单位:cm) Figure 7 Comparison of pressure head contours (unit: cm) |
已有方法在模拟边坡降雨入渗时,出现坡面径流(或超渗产流)后将坡面水深近似为0处理;忽略坡面水深同时,也忽略了径流对入渗的流量补给。所建新方法虽然也将坡面水深近似为0处理,但是对非产流边界(未饱和坡表)的流量进行了修正,从而可以考虑径流对入渗的补给。
4 结语基于Richards方程、运动波方程和有限单元法,提出了一种简化的考虑径流流量补给的滑坡降雨入渗三维数值模拟方法。该方法根据地形和降雨强度确定径流的补给流量;根据入渗边界是否饱和确定边界类型:如果饱和,则边界类型视为定水头边界(水深为0);如果非饱和,则边界类型视为流量边界且根据径流补给流量修正边界流量大小。从而考虑了径流补给对滑体入渗的影响。
简单边坡降雨入渗的算例表明,径流流量补给对边坡入渗过程影响较大。考虑径流流量补给时才能保证计算结果水量平衡,正确反映降雨入渗大幅降低基质吸力的作用。
| [1] |
RICHARDS L A. Capillary conduction of liquids in porous mediums[J]. Physics, 1931, 1: 318-333. DOI:10.1063/1.1745010 |
| [2] |
TSAI T L, YANG J C. Modeling of rainfall-triggered shallow landslide[J]. Environ Geol, 2006, 50: 525-534. DOI:10.1007/s00254-006-0229-x |
| [3] |
娄一青. 降雨条件下边坡渗流及稳定有限元分析[J]. 水利学报, 2007(增刊1): 346-351. ( LOU Yiqing. Finite element analysis of slope seepage and stability due to rainfall infiltration[J]. Journal of Hydraulic Engineering, 2007(Suppl1): 346-351. (in Chinese)) |
| [4] |
李萍, 张琦, 陈小念. 降雨条件下饱和-非饱和土坡的渗流分析[J]. 兰州理工大学学报, 2007, 33(6): 115-118. ( LI Ping, ZHANG Qi, CHEN Xiaonian. Seepage analysis of saturated-unsaturated slope under rainfall[J]. Journal of Lanzhou University of Technology, 2007, 33(6): 115-118. (in Chinese)) |
| [5] |
沈银斌, 朱大勇, 蒋泽锋, 等. 降雨过程中边坡临界滑动场[J]. 岩土力学, 2013, 34(增刊1): 60-66. ( SHEN Yinbin, ZHU Dayong, JIANG Zefeng, et al. Critical slip field of slope in process of rainfall infiltration[J]. Rock and Soil Mechanics, 2013, 34(Suppl1): 60-66. (in Chinese)) |
| [6] |
唐栋, 李典庆, 周创兵, 等. 考虑前期降雨过程的边坡稳定性分析[J]. 岩土力学, 2013, 34(11): 3239-3248. ( TANG Dong, LI Dianqing, ZHOU Chuangbing, et al. Slope stability analysis considering antecedent rainfall process[J]. Rock and Soil Mechanics, 2013, 34(11): 3239-3248. (in Chinese)) |
| [7] |
张培文, 刘德富, 郑宏, 等. 降雨条件下坡面径流和入渗耦合的数值模拟[J]. 岩土力学, 2004, 25(1): 109-113. ( ZHANG Peiwen, LIU Defu, ZHENG Hong, et al. Coupling numerical simulation of slope runoff and infiltration under rainfall conditions[J]. Rock and Soil Mechanics, 2004, 25(1): 109-113. (in Chinese)) |
| [8] |
MORITA M, YEN B C. Modelling of conjunctive two-dimensional surface three-dimensional subsurface flows[J]. Journal of Hydraulic Engineering, 2002, 128(2): 184-200. DOI:10.1061/(ASCE)0733-9429(2002)128:2(184) |
| [9] |
HUSSEIN M, SCHWARTZ F W. Modelling of flow and contaminant transport in coupled stream-aquifer systems[J]. Journal of Contaminant Hydrology, 2003, 65(1/2): 41-64. |
| [10] |
PRUDIC D E, KONIKOW L F, BANTA E R. A new stream-flow routing (SFR1) package to simulate stream-aquifer interaction with Modflow-2000[R]. United States Geological Survey, Open File Report 2004-1042.
|
| [11] |
LIANG D, FALCONER R A, LIN B. Coupling surface and subsurface flows in a depth averaged flood wave model[J]. Journal of Hydrology, 2007, 337(1-2): 147-158. DOI:10.1016/j.jhydrol.2007.01.045 |
| [12] |
SPANOUDAKI K, STAMOU A I, NANOU-GIANNAROU A. Development and verification of a 3-D integrated surface water-groundwater model[J]. Journal of Hydrology, 2009, 375(3-4): 410-427. DOI:10.1016/j.jhydrol.2009.06.041 |
| [13] |
KOLLET S J, MAXWELL R M. Integrated surface-groundwater flow modeling: a free-surface overland flow boundary condition in a parallel groundwater flow model[J]. Advances in Water Resources, 2006, 29(7): 945-958. DOI:10.1016/j.advwatres.2005.08.006 |
| [14] |
童富果, 田斌, 刘德富. 改进的斜坡降雨入渗与坡面径流耦合算法研究[J]. 岩土力学, 2008, 29(4): 1035-1040. ( TONG Fuguo, TIAN Bin, LIU Defu. A coupling analysis of slope runoff and infiltration under rainfall[J]. Rock and Soil Mechanics, 2008, 29(4): 1035-1040. (in Chinese)) |
| [15] |
TIAN D, LIU D. A new integrated surface and subsurface flows model and its verification[J]. Applied Mathematical Modelling, 2011, 35(7): 3574-3586. DOI:10.1016/j.apm.2011.01.035 |
| [16] |
田东方, 郑宏, 刘德富. 考虑径流影响的滑坡降雨入渗二维有限元模拟及应用[J]. 岩土力学, 2016, 37(4): 1179-1186. ( TIAN Dongfang, ZHENG Hong, LIU Defu. 2D FEM numerical simulation of rainfall infiltration for landslide with considering runoff effect and its application[J]. Rock and Soil Mechanics, 2016, 37(4): 1179-1186. (in Chinese)) |
| [17] |
WOOLHISER D A, LIGGET J A. Unsteady, one-dimensional flow over a plane-the rising hydrograph[J]. Water Resources Research, 1967, 3(3): 753-771. DOI:10.1029/WR003i003p00753 |
| [18] |
李占斌, 鲁克新. 透水坡面降雨径流过程的运动波近似解析解[J]. 水利学报, 2003(6): 8-13, 21. ( LI Zhanbin, LU Kexin. Approximate analytical solution of rainfall runoff process on permeable slope[J]. Journal of Hydraulic Engineering, 2003(6): 8-13, 21. (in Chinese)) |
 2017
2017 
