2. 河海大学 港口海岸与近海工程学院,江苏 南京 210098
我国黄、渤海沿岸分布着很多沙质海岸,中值粒径D50普遍为0.1~0.5 mm。由于特殊的地理环境,受到宽广的大陆架影响,波高常年较小,受风暴潮影响不大,破波带很窄且靠近岸线,破波带内无剧烈的泥沙输运,岸滩长期演变需考虑非破碎波的影响,可以称这部分海岸为低能沙质海岸[1]。这些低能沙质海岸中不乏有旅游胜地,如北戴河、青岛、烟台等地的旅游海滩,有着重要的经济和社会价值。因此,研究低能沙质海岸地貌动力,对于认识沙质海岸动力过程和黄、渤海沿岸旅游海滩的保护有重要意义。
采用物理试验方法研究沙质海岸动力过程可以直观地反映特定自然条件下的地貌变化,是研究海岸演变和海岸剖面变化的重要手段。其中对试验比尺的推导是波浪泥沙试验的重要基础,比尺效应更是试验中不可忽视的影响因素。对于海岸演变的问题,开展物理模型试验所遇到的比尺效应主要是由所选取的模型沙不能满足泥沙运动相似,特别是泥沙起动、沉降相似所引起的比尺效应[2],能否克服泥沙运动不相似带来的比尺效应直接关系到试验结果准确性的高低[3]。
对于波浪泥沙试验来讲,泥沙起动和沉降过程是试验关注的两个主要过程,其比尺推导的控制参数分别为希尔兹数和泥沙沉速。这两个参数的经典表达式均为分段式,如希尔兹曲线在光滑层流区、紊动光滑区(过渡区)、紊动粗糙区有不同的表达式,泥沙沉速在滞性状态、过渡状态、紊动状态也有着不同的表达式。这两个参数均存在“两边简,中间繁”的特点,光滑端和紊动端均有简单的规律,但在中间的过渡区表达式非常复杂,无法直接推导比尺关系[4-5]。因此,在经典的泥沙试验理论中,通常只给出光滑端和紊动端的比尺关系,而过渡段往往要具体问题具体分析,例如文献[6-7]中对于沉速比尺和起动比尺的处理。特别是当限于试验条件,泥沙粒径的几何比尺无法满足而必须选用轻质模型沙时(按照模型几何比尺推算后,模型沙粒径过小引起泥沙性质的改变),比尺的推算更为复杂。
对于低能沙质海滩,在岸线到闭合水深(或称界限水深,指存在剖面演变的水深范围)范围内,非破碎波引起的泥沙输运占主导地位,其泥沙起动和沉降的水流状态基本处于过渡状态;而在实验室研究选用轻质模型沙时,过渡状态的起动和沉降过程给比尺的推导带来了一系列麻烦。为了解决试验比尺设计困难的问题,本文针对低能沙质海岸剖面变化规律的波浪动床模型,提出了一种局部拟合方法,在现有的对泥沙运动过程认识的基础上,用于研究低能沙质海岸剖面变化规律物理模型的比尺推导。该方法绕过复杂的表达式问题,不仅限于解决本文遇到的比尺推算问题,对于海岸动力、河流动力模型里面其他难以进行比尺推算的复杂情况,在限定的研究范围内,也能很好地解决比尺推算问题。
1 设计方法 1.1 动床模型相似参数对于水流相似的相似参数,因为相对比较成熟,故不再赘述。重点关注泥沙相关的无量纲数。波浪作用下的泥沙运动通过π定理可推求4个无量纲参数:沙粒雷诺数U*D/υ、弗劳德数ρU*2/((ρs-ρ)gD)、无量纲密度参数ρs/ρ及沙粒几何相似参数λ/D。这4个无量纲参数在不同文献中可能表达式略有差别,但总体一致。Kamphuis将这4个参数表示为[8]:
| $ {{\Pi }_{\mathit{A}}}=\phi (\frac{{{\mathit{U}}_{*}}\mathit{D}}{\upsilon}, \frac{\rho {{\mathit{U}}^{2}}_{*}}{{{\mathit{\gamma }}_{\rm{s}}}\mathit{D}}, \frac{{{\rho }_{\rm{s}}}}{\rho }, \frac{\lambda }{\mathit{D}}) $ | (1) |
式中:D和ρs分别为泥沙颗粒粒径和干密度,表征了泥沙颗粒特性;切向速度
目前较广泛采用的解决方法之一是Dean提出的最优模型(Best Model)[9]。Dean在重力相似准则所计算出的模型几何比尺基础上,推算了模型沙所采用的相似比尺,他设定模型所选用的模型沙仍然是天然沙,只是粒径与原型不同,根据泥沙起动和沉降规则,计算了泥沙沉速比尺以及泥沙起动相似判别式。对于4个无量纲参数,最优模型除沙粒雷诺数不满足相似条件外,其余3个无量纲参数都可满足。Dean认为沙粒雷诺数不需要满足,很多情况下也可以满足试验精度,原因有二:一是研究破波带内泥沙输运时,底床泥沙运动的主要影响因素是波浪破碎引起的水流紊动,而不是底部切应力的作用;二是在紊动状态下,即原型与模型的泥沙雷诺数换算为泥沙流体参数满足S*>2,弗劳德数(ρU*2/(ρs-ρ)gD)接近于一个常数,泥沙雷诺数的变化对模型的影响可以忽略。但对于低能沙质海岸波浪动床模型,Dean给出的条件并不能完全适用:第一,由于波浪能较低,波浪破碎造成的紊动强度较小,相比来看,底部切应力对于底床泥沙运动的影响不可忽略;第二,由希尔兹起动曲线可知,通常认为S*>70时,即天然沙粒径ds>2 mm时才可认定为紊动起动,而低能沙质海岸天然沙粒径不属于这个范围[7]。
对于本文研究的低能沙质海岸,天然沙中值粒径为0.1~0.5 mm,若满足模型沙粒径大于0.08 mm,则可选取的几何比尺范围很小,模型尺度将非常大,在有限的试验条件下无法完成大范围区域的模拟。针对这种情况,可以采用轻质模型沙,选择性地根据前两个无量纲数(也就是沙粒雷诺数和无量纲弗劳德数)来设计试验比尺,后两个参数(无量纲密度参数和沙粒几何相似参数)不能满足。由于沙粒雷诺数和无量纲弗劳德数分别对应泥沙起动和沉降过程,满足了前两个参数,可以认为基本满足了动床演变规律上的相似,后两个参数的不满足,可以通过冲淤比尺的计算来弥补。这种模型在某些文献里面被称作轻质模型(LWM)[10]。虽然轻质模型也会有一些缺点,如模型沙形状一般较为规则,无法模拟天然沙的不规则形态等[11],但可以解决较大研究区域无法在有限试验场地内模拟的问题。
1.3 比尺关系推求问题的提出根据以上对模型选择的考虑,在试验场所有限的情况下,基于泥沙起动和沉降过程进行比尺设计是解决低能沙质海岸波浪动床模型的最佳选择之一。因此对于研究低能沙质海岸变化规律的波浪动床模型,其比尺设计的问题就转化为了确定泥沙起动比尺和沉速比尺的问题。但是在波浪作用下的泥沙运动过程中,由于泥沙粒径的大小会影响到波浪边界层的紊动状态,以及泥沙沉降时绕流的紊动状态,进而影响其沉降和起动的规律,且研究区域是我国渤海、黄海沿岸常见的沙质海岸,其粒径范围(0.1~0.5 mm)较大,起动、沉降规律更为复杂,使其比尺设计更加困难。
对于泥沙沉速比尺的计算,通常根据颗粒绕流的不同流态来计算泥沙沉速[12-13],这些公式大同小异,基本按照层流、紊流和过渡状态来分类讨论。在层流和紊流状态,因为影响因素相对单一,其沉速表达式相对简单,据此推出的沉速比尺不存在太大疑义,已经广为接受[5]。但是在层、紊流过渡状态,也正是沙质海岸所处的状态,由于泥沙沉降过程中,表面阻力和形状都不可忽略,其理论表达式又非常复杂,如Rubey,Soulsby,van Rijn等提出的公式[5, 14],不适合进行比尺计算。因此,对于绕流在层、紊流过渡状态的泥沙沉降的比尺推算,尚无广泛接受的方法。
对于泥沙起动比尺的计算,通常的判断依据是希尔兹曲线。在Dean的最优模型比尺推导中,认为希尔兹数的相似可不满足,与上文中提到的沙粒雷诺数不需要满足是一致的,因为希尔兹数可看作沙粒雷诺数的函数。Dean给出的解释是破波带内,底床泥沙运动的主要影响因素是波浪破碎引起的水流紊动,而不是底部切应力作用,即希尔兹曲线判别不再适用。但对于低能沙质海滩来说,Dean的解释并不适用,因为低能沙质海滩波高相对较小,水动力因素影响较弱,底部水流切应力的作用对于泥沙起动影响成为主要因素,所以低能沙质海滩动床模型的比尺设计需要考虑希尔兹数相似。希尔兹数相似的比尺设计和沉速相似的比尺设计面临同样问题,希尔兹曲线是一条非单调曲线,其数值分布规律会受到波浪边界层紊动强度的影响,难以找到一个通用方法来描述。这同样给泥沙起动比尺的推求造成了麻烦。
1.4 局部拟合法为了克服以上问题,解决低能沙质海滩波浪动床模型的泥沙沉降和起动比尺设计的困难,参考了文献[7]处理希尔兹曲线时用到的方法,提出了一种局部拟合方法,在现有的对泥沙沉降和起动过程认识的基础上,用于低能沙质海滩泥沙起动比尺和沉速比尺的推导。
局部拟合法是针对研究海岸泥沙类型等特定自然因素,选择最适合解决问题的泥沙沉速和起动公式,在研究的泥沙参数范围内计算数据点;再以这些数据点为基础,采用方便比尺推导的表达式,在研究的泥沙参数范围内对函数关系进行重新拟合,利用得到的新关系进行比尺推导。
研究对象为低能沙质海滩,其泥沙粒径D50范围为0.1~0.5 mm,进行比尺缩放以后,采用轻质模型沙的粒径范围亦在此范围内。因此,以此范围为例,首先考虑沙质海岸模型试验所有应该满足的相似参数;再根据相似参数不能同时满足的实际情况以及低能海滩的限定条件,优先满足沙粒雷诺数和弗劳德数这两个相似参数;这样比尺设计关键便转化为满足泥沙起动相似和沉降相似,即确定泥沙起动和沉速比尺;最后基于局部拟合法,分别选取合适的计算公式,对泥沙起动和沉速比尺进行推导。
2 泥沙起动比尺泥沙起动判别式是判断泥沙是否在底部水流切应力作用下脱离底床,被水流挟带并随水流方向移动的重要关系式。通过泥沙起动判别式所推求的泥沙起动比尺关系可以很好地帮助试验模型还原原始状态下泥沙的起动,保证了泥沙输运的基本规则不被改变,对选定试验模型沙有很大作用。泥沙起动判别式在光滑层流区和粗糙紊动区的表达式可以精确地给出,并为推算模型比尺所用,但是在过渡区仍无法给出简洁的表达形式。根据局部拟合法的原理,对于层流及紊动区的划分可以不予考虑,只需将研究范围内的曲线进行简化拟合,从而可以得到最符合试验要求的泥沙起动比尺关系。
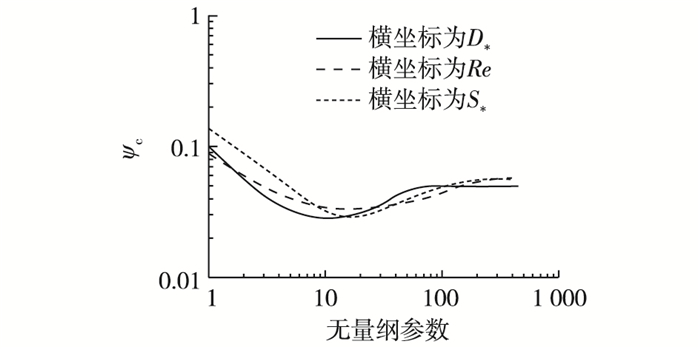
2.1 起动判别式的选取波浪作用下的泥沙起动规律与临界希尔兹数密切相关,单向波浪水流作用下,临界希尔兹数只与泥沙颗粒雷诺数Re=U*D/υ有关。基于前人大量的试验研究结果,可以确定雷诺数与希尔兹数的关系,并称之为希尔兹起动关系曲线,研究表明希尔兹起动关系曲线适用于波浪作用下的泥沙起动的判别。原始希尔兹曲线如图 1所示。
|
图 1 不同类型的希尔兹曲线 Figure 1 Different kinds of critical Shields curves |
由于临界希尔兹数与泥沙颗粒雷诺数的表达式中都含有U*,原始希尔兹曲线在应用时存在横、纵坐标数值同时变化的问题,不便于数据读取,因此Madsen等将希尔兹曲线转化为临界希尔兹数ψc和泥沙流体参数S*之间的关系[8],由此得到了ψc与S*的关系曲线如图 1。
Soulsby等在Madsen的基础上又对希尔兹曲线进行了改进[9],他将希尔兹曲线转化为临界希尔兹数ψc与无量纲颗粒尺寸参数D*之间的关系,关系曲线如图 1。
| $ \text{上述关系中}{{\psi }_{\text{c}}}\text{的表达式为:}\ \ \ \ \ \ \ \ \ \ {{\psi }_{\text{c}}}\text{=}\frac{{{\tau }_{\text{mc}}}}{\left( {{\rho }_{\text{s}}}-\rho \right)gD}~ $ | (2) |
| $ {{\mathit{S}}_{*}}\rm{的表达式为:}\ \ \ \ \ \ \ \ \ \ \ \ \ {{\mathit{S}}_{*}}=\frac{\mathit{D}\sqrt{\left( \mathit{s}-1 \right)\mathit{gD}}}{4\upsilon ~} $ | (3) |
| $ {{D}_{*}}\rm{的表达式为:}\ \ \ \ \ \ \ \ {{\mathit{D}}_{*}}=\mathit{D}{{\left[\left( \mathit{s}-1 \right)\frac{\mathit{g}}{{{\upsilon }^{2}}} \right]}^{\frac{1}{3}}} $ | (4) |
式中:τmc为底部临界切应力幅值;ρs为泥沙颗粒干密度;ρ为海水密度;s=ρs/ρ;D为泥沙颗粒粒径;υ为水体运动黏滞系数。
从图 1可以看出,在横坐标值小于10的区域,曲线接近于一条倾斜直线,而在Re大于100,S*和D*大于300的时候,曲线基本为一条水平直线,也就是说ψc为一定值。根据这个规律,希尔兹曲线可被分为光滑层流区,即Re<10的区域,这一区域内临界希尔兹数ψc的值与泥沙粒径无关;粗糙紊动区,即Re>100的区域,这一区域内临界希尔兹数ψc的值接近常数0.05;以及过渡区,即曲线中光滑层流区与粗糙紊动区中间的区域,这部分区域的临界希尔兹数ψc的值不易通过计算确定。
针对我国渤海、黄海的低能沙质海岸泥沙特点,选取粒径在0.1~0.5 mm范围内的曲线段,即1.01<S*<11.25或2.53<D*<12.65,由于ψc与Re的关系曲线中ψc与Re都含有U*,无法做到两个变量不相关,因此不考虑使用其做局部拟合。观察图 1可以发现,ψc与S*的关系曲线在这一范围内有明显弧度,直接作为直线拟合必然会导致拟合后的关系式失真,而以二次曲线形式拟合得到的关系式依然复杂,无法达到推求比尺的目的。反观ψc与D*的关系曲线,在2.53<D*<12.65的范围内更接近一条直线,因此以ψc与D*的关系曲线作为基础,对2.53<D*<12.65范围内的曲线进行局部拟合,从而得到所希望的简单希尔兹曲线公式。
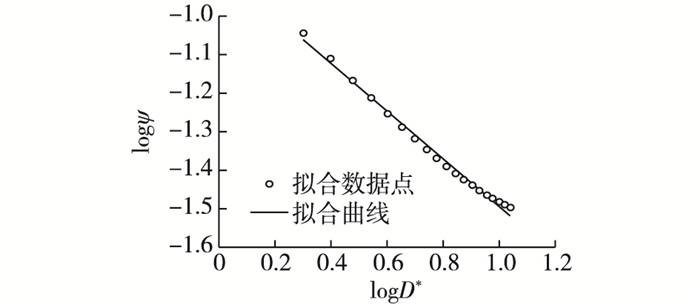
2.2 局部拟合法推求比尺根据前文提出的局部拟合法,以线性拟合的方式对图 1中关系曲线2.53<D*<12.65范围内的部分进行重新拟合,最终得到在对数坐标下ψc与D*的一次线性关系式:
| $ \rm{lg}{{\psi }_{\rm{c}}}=-0.62\rm{lg}{{\mathit{D}}_{*}}-0.88 $ | (5) |
式(5) 拟合结果的优劣可通过确定系数R(Coefficient of determination)来反映,确定系数的算法是用拟合后数据点与原始数据点平均值差的平方和除以原始数据点与原始数据点平均值差的平方和,R的表达式为:
| $ \mathit{R}=\frac{\sum\limits_{i=1}^{n}{{{w}_{i}}{{\left( {{{\hat{y}}}_{i}}-{{{\bar{y}}}_{i}} \right)}^{2}}}}{\sum\limits_{i=1}^{n}{{{w}_{i}}{{\left( {{y}_{i}}-{{{\bar{y}}}_{i}} \right)}^{2}}}}\rm{ } $ | (6) |
式中:
|
图 2 一次线性关系拟合临界希尔兹数与泥沙颗粒尺寸参数 Figure 2 Linear fitting curve of critical Shields number and sediment particle size parameter |
根据线性拟合得到的对数坐标下ψc与D*的一次线性关系式(5),可推求出更简洁的泥沙起动判别式,将关系式(5) 中对数运算去除得到ψc与D*的直接表达式:
| $ {{\psi }_{\rm{c}}}=0.13\mathit{D}_{*}^{-0.62} $ | (7) |
将ψc与D*各自相应的表达式代入式(7) 中,则式(7) 变为:
| $ \frac{{{\tau }_{\rm{mc}}}}{\left( {{\rho }_{\rm{s}}}-\rho \right)\mathit{gD}}~=0.13{{\left\{ \mathit{D}{{\left[\left( \mathit{s}-1 \right)\frac{\mathit{g}}{{{\upsilon }^{2}}} \right]}^{1/3}} \right\}}^{-0.62}} $ | (8) |
式中:底部临界切应力幅值τmc=0.5ρfwUmc2,fw为波浪摩阻系数;Umc为水底临界轨迹速度幅值。对于fw的确定,许多学者提出了不同的研究成果,分别对水流的层流、光滑湍流、粗糙湍流的不同区域进行了精确计算,得出了很多经验公式。为了能判断近底水流流态以确定fw的表达式,根据研究区域为低能沙质海滩这一条件,使用Jonsson (1966) 提出的波浪边界层流态的判别方法,计算得出在低能沙质海滩的大多数情况下,边界层雷诺数满足1.2×104<Re<4.2×105,符合光滑湍流状态的条件[15],即104<Re<106, amc/Δ>103,其中:Re为波浪作用下的边界层雷诺数,Re=Umcamc/υ,amc为底部水质点最大运动幅值,Δ为当量糙度,对于平坦床面Δ=D,对于沙纹床面Δ=η,η为沙纹高度[15]。
确定波浪边界层属于光滑湍流状态后,可以依据Jonsson的理论得到波浪摩阻系数计算式[13]:
| $ {{\mathit{f}}_{\rm{w}}}=0.09{{\left( {{\mathit{U}}_{\rm{mc}}}{{\mathit{a}}_{\rm{mc}}}/\mathit{v} \right)}^{-0.2}} $ | (9) |
值得注意的是,因为不同的波浪边界层状态中,波浪摩阻系数的变化规律有所差异,因此在选沙时应使模型和原型的波浪边界层处于同等紊动状态。
根据式(9) 对式(8) 进行化简,可以得到粒径在0.1~0.5 mm范围内的天然沙在波浪作用下的泥沙起动判别式:
| $ \mathit{U}_{\rm{mc}}^{1.80}/\left[{{\left( \mathit{s}-1 \right)}^{0.79}}{{g}^{0.79}}{{D}^{0.38}}{{\upsilon }^{0.21}} \right]=2.96\mathit{a}_{\rm{mc}}^{0.20}~ $ | (10) |
将式(10) 写成比尺关系:
| $ \lambda _{{{\mathit{U}}_{\rm{mc}}}}^{1.80}/\left( \lambda _{\mathit{s}-1}^{0.79}\lambda _{\mathit{D}}^{0.38} \right)=\lambda _{{{\mathit{a}}_{\rm{mc}}}}^{0.20} $ | (11) |
根据波浪相似准则可知,
| $ {{\lambda }_{\rm{h}}}=\lambda _{\mathit{s}-1}^{1.14}\lambda _{\mathit{D}}^{0.55} $ | (12) |
泥沙沉速比尺关系可以反映模型沙脱离水流的挟带沉降到底床的速度关系,对于研究岸滩演变及泥沙输运规律有重要影响。根据目前的研究成果,可以将泥沙在水中下沉的运动归纳为滞性状态、过渡状态和紊动状态等3种流动状态。当研究的泥沙颗粒下沉状态属于滞性状态和紊动状态时,泥沙沉速可通过确定的公式表达,而当下沉状态属于过渡状态时,沉速公式变得复杂且难以准确反映真实沉速。对于过渡状态的泥沙沉速公式可以使用局部拟合法,对所研究的泥沙粒径范围内的泥沙沉速进行重新拟合,得出适合研究使用的简单沉速公式,并依此推导出泥沙沉速比尺关系。
3.1 沉速公式的选取泥沙沉速是泥沙在静水中等速沉降的速度,是在水流挟沙力等于泥沙颗粒自重时计算得出,它的影响因素包括泥沙颗粒干密度、颗粒粒径和颗粒形状。当泥沙开始沉降时泥沙重力大于阻力,下沉运动加速后阻力增大,达到与重力相等,此时可得到泥沙最终沉速为:
| $ \mathit{\omega }=\sqrt{\frac{4}{3}\frac{{{\rho }_{\rm{s}}}-\rho }{\rho }\frac{\mathit{gD}}{{{\mathit{C}}_{\rm{D}}}}} $ | (13) |
此式中只要确定泥沙阻力系数CD便可求得泥沙沉速,经过大量理论及试验研究,可确定泥沙颗粒下沉状态属于滞性状态时,即Re<0.1时,泥沙沉速可表达为[14]:
| $ \omega =\left( \mathit{s}-1 \right)\mathit{g}{{\mathit{D}}^{2}}/\left( 18v \right), \rm{ }\mathit{D}<0.05\ \rm{mm} $ | (14) |
紊动状态,即Re>500时,泥沙沉速可表达为[12]:
| $ \omega =1.1\left[ \left( s-1 \right)gD \right]{{~}^{0.5}},D>1.80\ ~\text{mm}~ $ | (15) |
以上推导得出的结论便是经典的斯托克斯定律[12],在计算滞性状态和紊动状态的泥沙沉速时,具有极高准确度而被广泛使用。式(14) 和(15) 不仅具备精确性,其简洁表达方式也为物模试验计算比尺提供了便利,因此在模拟处于滞性状态和紊动状态的泥沙沉降时,可直接得到沉速比尺,毋需进行局部拟合。然而对于粒径在0.05<D<1.80 mm范围内的泥沙颗粒,其下沉状态属于过渡状态,沉速公式无法通过简单公式推导得出,一般通过试验给出半经验半理论公式。沉速公式普遍形式复杂且多种多样,适用范围各不相同,对于得到过渡区泥沙沉速比尺造成了困难。
Rubey提出一种半经验的处理方法[14],即假定过渡区内阻力表达式可写为黏滞阻力和形状阻力的叠加,则沉速可表达为:
| $ \omega =-4\frac{{{\mathit{k}}_{2}}}{{{\mathit{k}}_{1}}}\frac{\upsilon }{\mathit{D}}+\sqrt{\left( 4\frac{{{\mathit{k}}_{2}}}{{{\mathit{k}}_{1}}}\frac{\upsilon }{\mathit{D}} \right){{~}^{2}}+\frac{4}{\rm{3}{{\mathit{k}}_{1}}}~\frac{{{\rho }_{\rm{s}}}-\rho }{\rho }\mathit{gD}} $ | (16) |
Soulsby提出了用泥沙粒径D和颗粒尺寸参数D*作为变量表达泥沙沉速的关系式[16]:
| $ \omega =\frac{\mathit{D}}{\upsilon }(\sqrt{{{10.36}^{2}}+1.049\mathit{D}_{*}^{3}}-10.36)~ $ | (17) |
van Rijn将泥沙沉速分为3个分段函数表达[5, 17]:
| $ \omega =\left\{ \begin{align} &\frac{\left( \mathit{s}-1 \right)\mathit{g}{{\mathit{D}}^{2}}}{18\upsilon }, \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 1~\mu \rm{m}\mathit{<D}\le \rm{0}\rm{.1}\ \rm{mm} \\ &\frac{10\upsilon }{\mathit{D}}\left[{{\left( 1+\frac{0.01\left( \mathit{s}-1 \right)\mathit{g}{{\mathit{D}}^{3}}}{{{\upsilon }^{2}}} \right)}^{0.5}}-1 \right], \ \ \ \ \ ~0.1\ \rm{mm}\mathit{<D}<\rm{1}\ \rm{mm} \\ &1.1{{\left[\left( \mathit{s}-1 \right)\mathit{gD} \right]}^{0.5}}, \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ D\ge 1\ \rm{mm} \\ \end{align} \right. $ | (18) |
从形式上看,式(18) 的表达方式复杂;从精确度上看,式(16) 中系数k1和k2需要试验确定,准确性有所降低,同时更增加了推求比尺的难度,因此不适合用作原始公式进行拟合。式(17) 这种表达方法可以不区分流态获得各种泥沙粒径下的沉速公式,也基本可将不同粒径大小泥沙沉速表达精准,但D*的表达式过于复杂,且其中包含D,当D单独变化时D*也会受到影响产生变化,不利于公式拟合。
式(18) 在滞性状态和紊动状态下沉速公式与斯托克斯定律一致,仅粒径分段区间不同,其过渡状态的表达式可看做沉速ω与泥沙粒径D及相对(密度)(s-1) 的关系式,D与(s-1) 互不相关,可以作为原始公式进行局部拟合。对于低能沙质海岸,式(18) 的过渡状态分段恰好将研究海岸泥沙中值粒径范围0.1~0.5 mm包含在内,可以根据这一公式对0.1<D<0.5 mm范围内的泥沙沉速进行局部拟合,以得到较为简单的泥沙沉速公式。
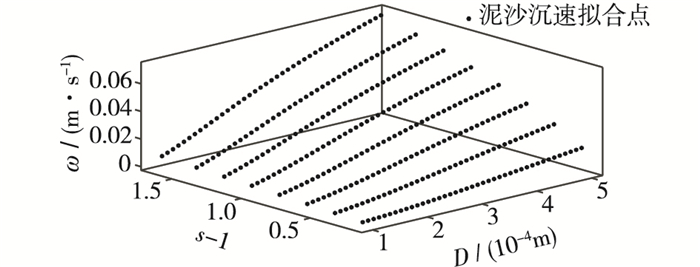
3.2 局部拟合法推求比尺使用式(18) 计算研究区域内不同干密度以及不同粒径沙的沉速曲线,再用空间曲面对沉速关系进行拟合。分析可知在一定温度下泥沙沉速主要与泥沙粒径和干密度相关,因此确定以泥沙粒径D(单位为m)作为x轴坐标,泥沙相对密度s-1作为y轴坐标,其中s=ρs/ρ,计算出的泥沙沉速ω值作为z轴坐标,绘制多个真实泥沙沉速空间点,如图 3所示。
|
图 3 泥沙沉速拟合点 Figure 3 Fitting points of sediment settling velocity |
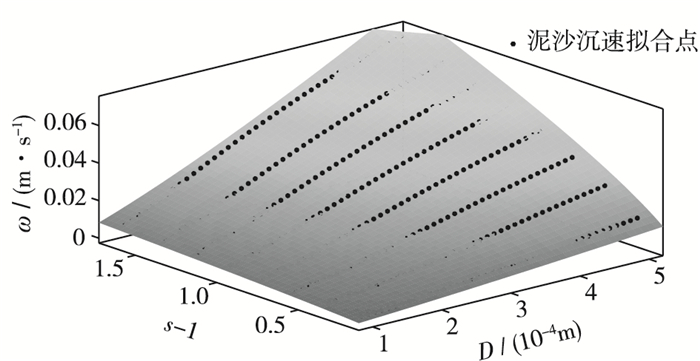
对这些空间点进行曲面拟合,拟合过程中尝试了许多种不同的形式,最终发现使用如式(19) 的关系式进行拟合时拟合度最高,这与夏益民等根据试验得出泥沙沉速推导的经验公式相似[7, 18],当改变研究粒径范围时这种形式依然可以得到拟合度很高的曲面如图 4。
| $ \omega =\mathit{a}{{\left( \mathit{s}-1 \right)}^{b}}\mathit{g}{{\mathit{D}}^{\mathit{c}}} $ | (19) |
|
图 4 曲面拟合泥沙沉速关系 Figure 4 Sediment deposition velocity relationships by using surface fitting method |
根据拟合结果可得泥沙粒径在0.1~0.5 mm范围内的不同干密度泥沙的沉速值,拟合结果的确定系数R达到0.993,接近于完全相关,RMSE值等于0.001 6,也证明了拟合效果非常好,因此研究区域内泥沙沉速基本符合式(20) 所计算出的结果:
| $ \omega =68.71\left( \mathit{s}-1 \right)0.72\mathit{g}{{\mathit{D}}^{1.24}}~ $ | (20) |
根据式(20),可以得到研究区域泥沙粒径在0.1~0.5 mm、泥沙干密度在1.20~2.65 g/cm3范围内的泥沙沉速比尺关系:
| $ {{\lambda }_{\omega }}=\lambda _{\mathit{s}-1}^{0.72}\lambda _{\mathit{D}}^{1.24} $ | (21) |
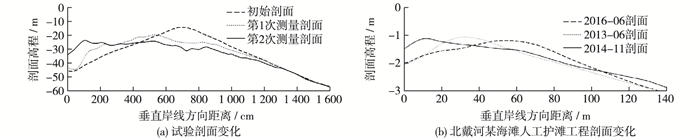
使用局部拟合法推导出的相似比尺关系式被用于北戴河某海滩人工护滩工程,以研究人工护滩后的海滩剖面变化过程。试验采用正态模型,天然沙中值粒径为0.3 mm,综合考虑现场数据和实验室条件,设定几何比尺为8。根据确定的模型沙粒径范围0.1~0.5 mm,可以给定泥沙粒径比尺λD的范围为0.6~3.0,再根据所提供的比尺关系,可以通过式(12) 确定泥沙相对密度比尺3.65≤λs-1≤7.93,相应计算出所选轻质模型沙密度范围应为1.21~1.45 g/cm3。由于符合这一条件范围的轻质模型沙类型较少,综合考量选定符合这一条件范围且对天然沙模拟效果较好的核桃沙(ρs=1.44 g/cm3)作为轻质模型沙,并使用式(12) 计算选定模型沙的粒径比尺为0.11 mm。
根据上述比尺设计进行低能沙质海岸剖面波浪动床模型的试验研究,结果显示海滩剖面的变化与实测地形剖面变化趋势一致,剖面形状特征基本吻合,如图 5所示,充分证明了本文的分析与推导能够较好地应用于低波浪能状态下的波浪动床物模试验研究。
|
图 5 北戴河某海滩人工护滩工程剖面与物模试验剖面对比 Figure 5 Comparison between profiles of an artificial nourishment project in Beidaihe and profiles given by physical model experiments |
针对长期以来一直影响海岸波浪动床物理模型试验精确度的物理模型比尺问题进行了探讨,并结合各种现有的物理模型比尺设定方法,针对低能沙质海滩的特征,选定了轻质模型理论作为比尺设计的依据。
低能沙质海滩的泥沙起动和沉降均处于层流、紊流的过渡状态,计算方法复杂且无统一公认的公式,给比尺推求带来了诸多困难。针对此问题,提出了局部拟合法,将问题聚焦到研究范围,选用合适的方法在研究范围内计算得到一定的数据点,然后使用简单的形式拟合得到在研究范围内可用的简单表达式,在此基础上进行比尺推算,从而成功规避了复杂公式无法进行比尺推算的矛盾。
针对低能沙质海岸波浪动床模型的比尺推算问题,基于局部拟合法,对泥沙起动和泥沙沉速比尺进行了推算,得到了泥沙起动比尺关系λh=λs-11.14λD0.55和泥沙沉速比尺关系λω=λs-10.72λD1.24,以这两个比尺关系进行设计的波浪动床试验取得了良好试验效果。
提出的局部拟合法思路不仅限于解决针对低能沙质海岸波浪动床模型的比尺推算问题,对于海岸动力、河流动力模型里面其他难于进行比尺推算的复杂问题,在限定的研究范围内,也能很好地解决比尺推算问题。
| [1] |
DOUCETTE J S. Bedform migration and sediment dynamics in the nearshore of a low-energy sandy beach in southwestern Australia[J]. Journal of Coastal Research, 2002, 18(3): 576-591. |
| [2] |
王玉海, 蒋卫国, 王艳红. 冲刷物理模型试验的比尺效应研究[J]. 泥沙研究, 2012(3): 31-34. ( WANG Yuhai, JIANG Weiguo, WANG Yanhong. A study of scale effect in scour physical-model experiments[J]. Journal of Sediment Research, 2012(3): 31-34. (in Chinese)) |
| [3] |
朱立俊, 赵晓冬. 模型变率对斜坡上泥沙起动相似影响研究[J]. 海洋工程, 1997, 15(2): 65-73. ( ZHU Lijun, ZHAO Xiaodong. The impact of scale distortion on the similarity of incipient motion on river gradient bed[J]. The Ocean Engineering, 1997, 15(2): 65-73. (in Chinese)) |
| [4] |
邹志利. 海岸动力学[M]. 北京: 人民交通出版社, 2009: 146-187. ( ZOU Zhili. Coastal hydrodynamics[M]. Beijing: China Communications Press, 2009: 146-187. (in Chinese))
|
| [5] |
IMIS V, VAN RIJN L C. Principles of sediment transport in rivers, estuaries and coastal seas[J]. Morfologie Morf, 1993, 185-201. |
| [6] |
窦国仁. 全沙模型相似律及设计实例[J]. 水利水运工程学报, 1977(3): 3-22. ( DOU Guoren. A similarity theory concerning the design of total sediment transport models with reference to a particular project[J]. Hydro-Science and Engineering, 1977(3): 3-22. (in Chinese)) |
| [7] |
夏益民, 段子冰, 徐华, 等. 波浪作用下海岸泥沙运动规律和模型相似律研究[C]//第十三届中国海洋(岸)工程学术讨论会论文集. 北京: 海洋出版社, 2007: 230-237. (XIA Yimin, DUAN Zibing, XU Hua, et al. Study on the law of coastal sediment movement and model similarity under the action of waves[C]//The 13th China Ocean (Shore) Engineering Symposium Proceedings. Beijing: China Ocean Press, 2007: 230-237. (in Chinese))
|
| [8] |
KAMPHUIS J W, NAIRN R B. Scale effects in large coastal mobile bed models[C]//19th International Conference on Coastal Engineering. Virginia: ASCE, 2012: 2322-2338.
|
| [9] |
DALRYMPLE R A. Physical modelling of littoral processes[M]. Netherlands: Kluwer Academic Publishers, 1989: 567-588.
|
| [10] |
KAMPHUIS J W. Coastal mobile bed model—does it work[C]//Proceedings of the 2nd Symposium on Modeling Techniques. Virginia: ASCE, 2010: 993-1009.
|
| [11] |
KAMPHUIS J W. Introduction to coastal engineering and management[J]. World Scientific, 2015, 564. |
| [12] |
STOKES G G. On the effect of the internal friction of fluids on the motion of pendulums[J]. Transactions of the Cambridge Philosophical Society, 1851, 9(2): 8-106. |
| [13] |
OSEEN C W. Neuere methoden und ergebnisse in der hydrodynamik[J]. Monatshefte Für Mathematik Und Physik, 1928, 35(1): A67-A68. DOI:10.1007/BF01707470 |
| [14] |
RUBEY W W. Equilibrium conditions in debris laden streams[J]. Eos Transactions American Geophysical Union, 1933, 14(1): 497-505. DOI:10.1029/TR014i001p00497 |
| [15] |
JONSSON I G. Wave boundary layers and friction factors[C]//Tenth International Conference on Coastal Engineering, 1966: 127-148.
|
| [16] |
GRANT W D. Sediment transport in the coastal environment[M]. Massachusetts: Massachusetts Institute of Technology, 1976: 79-91.
|
| [17] |
VOOGT L, VAN RIJN L C, BERG J H V D. Sediment transport of fine sands at high velocities[J]. Journal of Hydraulic Engineering, 1991, 117(7): 869-890. DOI:10.1061/(ASCE)0733-9429(1991)117:7(869) |
| [18] |
夏益民. 沙质海岸波浪动床模型设计—毛里塔尼亚友谊港下游冲刷试验模型[J]. 海洋工程, 1994, 12(3): 42-53. ( XIA Yimin. Design of coastal mobile bed model of sandy beach-erosion test model of Youyi harbor downstream in Mauritania[J]. The Ocean Engineering, 1994, 12(3): 42-53. (in Chinese)) |
2. College of Harbor, Coastal and Offshore Engineering, Hohai University, Nanjing 210098, China
 2017
2017 
