2. 中国科学院大学,北京 100049;
3. 国家海洋局 第二海洋研究所 工程海洋学重点实验室,浙江 杭州 310012;
4. 广东海洋大学 海洋与气象学院,广东 湛江 524088
台风是浙江主要的海洋灾害之一,平均每年大约有3个台风影响浙江地区。浙江南部的温州、台州地区是最容易遭受台风灾害的区域,既受到浙江登陆台风的影响,又受到福建地区登陆台风的影响,且由于浙江南部位于福建登陆台风的危险右半圆区域,因此受到的台风破坏程度甚至比浙江登陆的更为严重。台风浪作为台风引起的海洋灾害之一,近岸的台风浪能够毁坏港口海岸工程,对海上交通和养殖业造成巨大威胁,因此深入研究台风浪的时空特征,对于港口运输、防灾减灾、海岸工程防护具有重要意义[1]。
在台风浪的数值模拟中,波浪场的模拟精度很大程度上依赖于海面风场的计算精度,常见的台风风场模型有藤田模型、Jelesnianski模型、Holland模型等。针对各个风场模型在台风浪计算中的适用性,许多学者进行了大量研究。黄文锋[2]利用中国东南沿海1949—2012年的台风历史数据进行香港地区台风关键参数概率分布的研究,提出了基于新的Holland径向气压分布参数B表达式的台风风场经验模型,提高了台风预报的时效性。张志旭[3]利用经验的Holland台风模型和NCEP再分析风场资料相结合构造出南海台风风场,结果较好地符合TOPEX/Poseidon(T/P)卫星高度计观测的风速分布,以此作为第三代海浪模式的输入风场,模拟了1999年York台风经过南海海域的台风浪。梁连松等[4]将Holland台风风场模型与CCMP背景风场相叠加,构造合成风场来驱动SWAN模型,研究了台风“米雷”通过舟山海域的波浪场。齐庆辉等[5]采用Jelesnianski风场模式风速作为波浪模式MIKE-SW的驱动风场,再现1210号台风“达维”登陆连云港海域波浪变化过程。何倩倩等[6]基于Jelesnianski风场模型和NCEP风场,利用SWAN模型对台风达维过境江苏期间的台风浪进行了研究。金罗斌[7]基于第三代海浪模式SWAN,利用Myers理论模型风场、CCMP风场以及两者的合成风场,分别作为台风驱动风场,对2003—2010年经过南海的15个台风浪过程进行数值模拟研究。通过与卫星高度计观测资料比较表明:Myers理论模型风场模式在台风中心附近波高较大时与实测值吻合较好,CCMP风场模式离台风中心较远处与实测值吻合较好。
总结前人研究成果可知,之前的研究实测资料多来自卫星数据,误差较大,而且对Holland风场模型各种参数缺乏比较分析,本文采用第三代海浪模型SWAN,选取Holland风场模型,比较不同Holland风场模型中最大风速半径和B参数计算组合对风场模拟精度的影响,选取最优组合,以1323号台风“菲特”为例,分析浙江南部海域的风浪分布特征和时空规律。
1 台风模型介绍1980年,Holland[8]在Schloemer指数气压分布模型基础上,引入Holland B参数,利用梯度风风场得到Holland台风风场如下:
| $ \rm{气压方程:}\ \mathit{p}\left( \mathit{r} \right)={{\mathit{p}}_{\rm{c}}}+\left( {{\mathit{p}}_{\rm{n}}}-{{\mathit{p}}_{\rm{c}}} \right){{(-\frac{{{\mathit{R}}_{\rm{max}}}}{\mathit{r}})}^{\mathit{B}}}~ $ | (1) |
| $ \rm{风场方程:}\ {{\mathit{V}}_{\mathit{g}}}\left( \mathit{r} \right)=\ \sqrt{\left( {{\mathit{p}}_{\rm{n}}}-{{\mathit{p}}_{\rm{c}}} \right)\ \frac{\mathit{B}}{{{\rho }_{\rm{a}}}}{{\left( \ \frac{{{\mathit{R}}_{\rm{max}}}}{\mathit{r}}\ \right)}^{\mathit{B}}}\rm{exp}{{\left( -\ \frac{{{\mathit{R}}_{\rm{max}}}}{\mathit{r}}\ \right)}^{\mathit{B}}}+{{\left( \ \frac{\mathit{rf}}{2} \right)}^{2}}}-\ \frac{\mathit{rf}}{2} $ | (2) |
式中:pc为台风中心气压;pn为外围气压;Rmax为最大风速半径;ρa为空气密度;f为科氏力参数;r为与台风中心的距离;B参数决定了台风的峰度和强度。
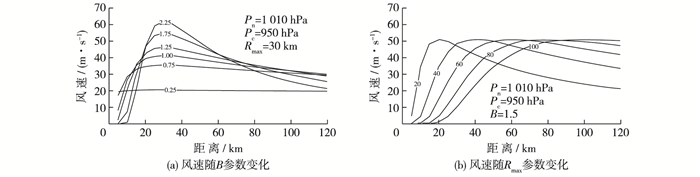
基于Holland风场的台风浪数值计算由式(1) 和(2) 可知,B参数和Rmax是决定Holland风场的两个关键参数。图 1(a)表明其他参数固定时,随着B参数的增加,最大风速半径处的风速也逐渐增加,而离台风中心较远位置的风速则变弱,风场能量更加集中。反之,风速大小则随距离分布比较平均。图 1(b)展示了其他参数固定时,风速随Rmax变化示意图。由图 1(b)可知,风速由台风中心向外侧逐渐增大,在最大风速半径处达到最大,然后逐渐减小,随着Rmax的增加,最大风速半径外的风速变化趋于平缓。
|
图 1 风速随B参数和Rmax参数变化曲线 Figure 1 Change curves of wind speed with parameters B and Rmax |
关于B参数的取值,Holland首先基于澳大利亚海域台风数据,给出B的合理取值范围为1.0~2.5。Hubbert[9]提出了适用于澳大利亚海域的经验参数B的计算式:
| $ \mathit{B}=1.5+\left( 980-{{\mathit{P}}_{\rm{c}}} \right)/120 $ | (3) |
Holland[10]考虑了台风过程中的气压、强度、所在纬度和移动速度等因素,重新改进了B参数计算式如下:
| $ {{\mathit{B}}_{\rm{s}}}=-4.4\times {{10}^{-5}}\mathit{\Delta }{{\mathit{p}}^{2}}+0.01\Delta\mathit{p}+0.03\partial \mathit{p}/\partial \mathit{t}-0.014\phi +0.15\mathit{V}_{\rm{t}}^{\mathit{x}}+1~ $ | (4) |
| $ \mathit{x}=0.6(1-\Delta\mathit{p}/215) $ | (5) |
| $ \mathit{B}=1.6{{\mathit{B}}_{\rm{s}}} $ | (6) |
式中:Δp为台风中心气压与外围气压之差(hPa);ϕ为纬度;Vt为台风前进速度(m/s)。
Willoughby等[11]基于丰富的飞机低空探测数据对台风模型的各个参数进行了最小二乘法拟合,研究显示随着风速增加,最大风速半径减小,而参数B则增大,拟合计算式如下:
| $ {{\mathit{R}}_{\rm{max}}}=51.6\rm{exp}(-0.022\ 3{{\mathit{V}}_{\rm{max}}}+0.028\ 1\phi )~ $ | (7) |
| $ \mathit{B}=1.003\ 6+0.017\ 3{{\mathit{V}}_{\rm{max}}}-0.031\ 2\rm{ln}{{\mathit{R}}_{\rm{max}}}+0.008\ 7\phi $ | (8) |
式中:Vmax为最大风速。
Vickery等[12]结合飞机探测和HRD观测数据对台风特征参数进行了统计分析,分别给出了最大风速半径和B参数的计算式如下:
| $ {{\mathit{R}}_{\rm{max}}}=\rm{exp}(3.015-6.291\times {{10}^{-5}}\Delta{{\mathit{p}}^{2}}+0.033\ 7\phi )~ $ | (9) |
| $ \mathit{B}=1.881-0.005\ 57{{\mathit{R}}_{\rm{max}}}-0.012\ 95\phi ~ $ | (10) |
综上所述,国内外学者对于B参数和Rmax进行了详尽研究,但大部分都是基于飞机探空数据对特定海区的研究,专门针对中国海域的台风研究比较少,而且我国缺乏风廓线上层风速观测数据,难以直接利用统计方法拟合台风参数。因此,结合已有的风场模型参数,利用台风期间测站风、波浪数据进行验证,选择适用于我国海域的台风参数并进行误差分析。为减小台风登陆引起的风场结构改变以及复杂地形的影响,本研究选取海岛测站和海洋浮标测站数据进行验证。
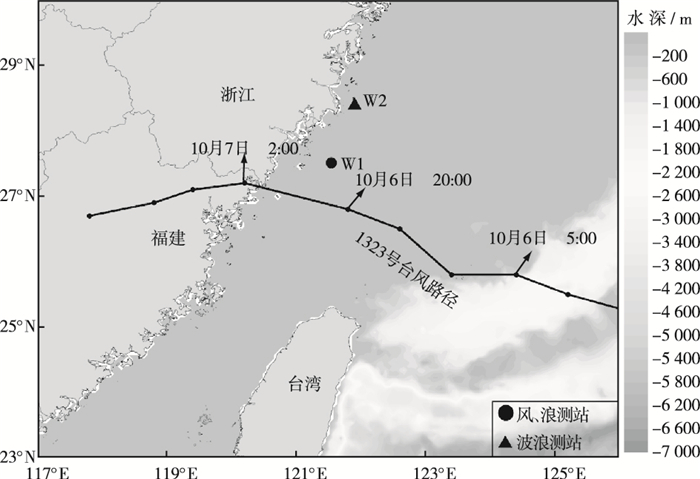
2 风场参数组合试验以1323号台风为例,分析模型风场与实测风速的误差。2013年第23号热带风暴“菲特”于2013年9月30日20:00在菲律宾以东洋面生成,10月1日20:00增强为强热带风暴,4日17:00增强为强台风,7日01:15在福建省福鼎市沙埕镇沿海登陆,登陆时中心最低气压为955 hPa,近中心最大风力14级,强度为强台风。“菲特”是建国以来10月份登陆我国大陆强度最强的台风,浙江、福建、江苏、上海紧急转移139.8万人,9 500余间房屋倒塌或严重损坏,直接经济损失高达623.3亿元,为近十年来单个台风直接经济损失最严重的一次。台风路径及各测站位置如图 2所示,W1为风、浪观测站,W2为波浪测站。
|
图 2 1323号台风“菲特”路径 Figure 2 Moving path of No.1323 typhoon "Fitow" |
为比较不同的Holland B参数和最大风速半径计算式构造出的台风风场对台风浪模拟精度的影响,设置了6组试验,试验设置如表 1所示。模型对比所需的实测风速资料来自海洋浮标W1站。台风路径及中心气压来源于中国气象局热带气旋资料的CMA最佳路径数据集。
| 表 1 试验方案设置 Table 1 Schemes of experiments |
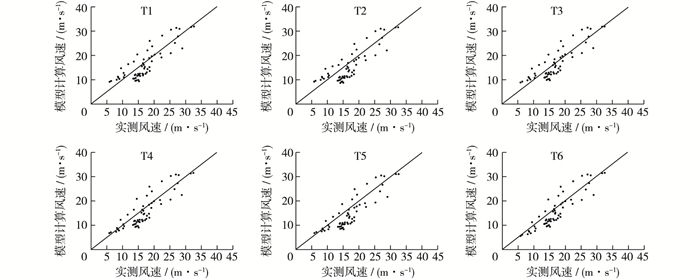
图 3为模拟风速与实测风速的对比,总体上,散点基本分布在y=x的两侧,表明模型风速计算结果较好,为了定量分析各个试验的模拟效果,寻找最优参数,我们采用均方根误差RSME对模型结果的准确性进行比较。
| $ \mathit{RSME}=\sqrt{\frac{1}{\mathit{N}}\sum\limits_{i=1}^{N}{{{\left( {{x}_{i}}-{{y}_{i}} \right)}^{2}}}} $ | (11) |
|
图 3 各方案模型风速与实测风速对比 Figure 3 Comparison between simulated and measured wind speeds |
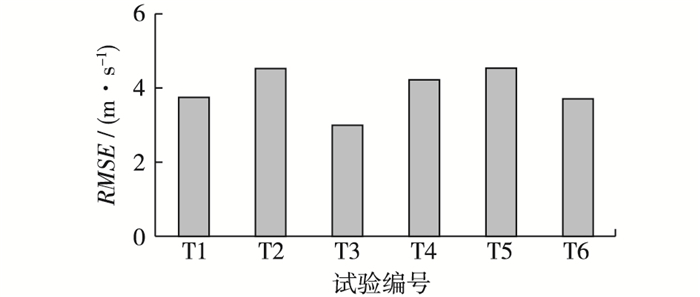
式中:yi为模型计算结果;xi为实测值;N为样本总数。各方案误差统计如图 4所示。
|
图 4 各方案试验误差统计 Figure 4 Statistics of experiment errors |
经误差计算可知:基于Holland台风模型对1323号“菲特”台风风速的模拟较好,对比6个方案可知,不同风速半径和不同B参数对风场模拟精度有较大影响,T3方案的模拟结果误差最小,优于其他方案,说明Willoughby提出的最大风速半径计算式和Vickery提出的B参数计算式组合对1323号台风的模拟误差最小。
3 台风浪模拟研究 3.1 波浪数学模型台风浪计算采用的波浪模型为SWAN模型,SWAN模型是Delft大学提出的考虑了波浪破碎、波波相互作用和白帽耗散等影响的第3代海浪数值模式,适用于近岸海域的波浪计算[13]。SWAN模型的控制方程为动谱密度守恒方程,在笛卡尔坐标下的表达式为:
| $ \frac{\partial \mathit{N}}{\partial \mathit{t}}+\frac{\partial {{\mathit{C}}_{\mathit{x}}}\mathit{N}}{\partial \mathit{x}}+\frac{\partial {{\mathit{C}}_{\mathit{y}}}\mathit{N}}{\partial \mathit{y}}+\frac{\partial {{\mathit{C}}_{\mathit{\sigma }}}\mathit{N}}{\partial \mathit{\sigma }}+\frac{\partial {{\mathit{C}}_{\mathit{\theta }}}\mathit{N}}{\partial \theta }=\frac{\mathit{S}}{\sigma } $ | (12) |
式中:动谱密度函数
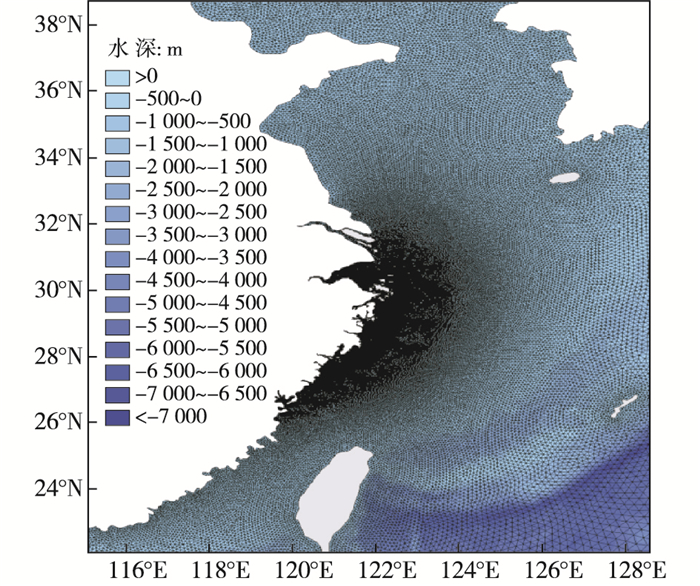
模型采用非结构三角网格,外海分辨率较低,网格尺度为5 000 m左右,近岸网格进行加密(见图 5),最高可达300 m,不同分辨率网格之间平滑过渡,既保证了计算效率又能保证岸线地形的准确性,也避免采用多重嵌套带来的计算误差。计算时间从2013年10月5—8日,时间步长取60 s。模型中考虑了海底摩擦、波浪破碎、三波和四波相互作用及绕射效应。模型所使用的地形资料来自于GEBCO全球地形数据集,近岸采用航保部海图水深数据。台风风场来自Holland T3方案参数生成的台风风场数据。
|
图 5 波浪模型计算范围和网格 Figure 5 Model calculation area and grids |
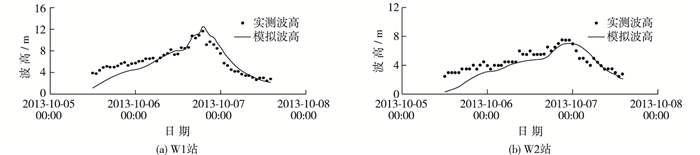
波浪验证资料选取W1和W2站的观测资料,模拟结果与实测结果对比曲线如图 6所示。由图 6可知,10月6日8:00以前模拟的有效波高偏小,但是有效波高的峰值拟合较好,两个站的波高峰值误差在0.25 m以内。总体而言,此次台风浪模拟结果良好,模型能够用于后续台风浪的特征分析。
|
图 6 模型与实测有效波高验证 Figure 6 Validation between model and measured avaliable wave heights |
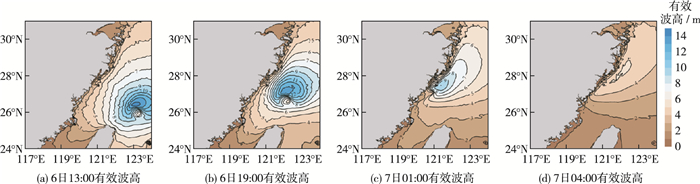
图 7给出了“菲特”台风过境期间浙江海域波高分布,当台风在外海时,台风中心海域的台风浪要远大于周边,中心区域有效波高超过12 m,随着台风的移动,最大波高位置也随之移动,越靠近岸边波高等值线分布越密集,与水下地形等深线分布基本一致,近岸浅水区域波浪衰减速度加快。当台风登陆时(图 7(c),温州海域的波高明显高于其他区域,有效波高最大达到10 m左右,当台风进入内陆以后,波高迅速减小至4 m左右。台风移动方向右侧有效波高相对较大,近岸地区受到地形、岛屿影响,分布和变化较外海更加复杂。
|
图 7 1323号“菲特”台风期间有效波高分布 Figure 7 Avaliable wave height distribution during No.1323 typhoon "Fitow" |
采用Holland台风模型,选取不同的最大风速半径和B参数进行组合,然后将模型构造风场与实测风速资料进行比较分析。结果表明,Willoughby风速半径公式和Vickery的Holland B参数经验公式组合后的计算误差最小。然后基于SWAN模型,模拟了1323号“菲特”台风过境期间浙江南部地区的台风浪。结果表明,最优组合参数生成的台风风场,对台风浪的模拟结果较好。外海台风中心有效波高超过12 m,台风移动方向右侧有效波高相对较大。当台风登陆时,温州地区的波高明显高于其他区域,中心最大波高超过10 m,当台风进入内陆以后,波高迅速减小至4 m左右。
| [1] |
郑祥靖. 潮汐和潮流作用下1323号台风"菲特"台风浪数值模拟[J]. 海洋预报, 2015, 32(5): 8-13. ( ZHENG Xiangjing. Numerical simulation of typhoon waves with tide during 1323 typhoon "Fitow"[J]. Marine Forecasts, 2015, 32(5): 8-13. DOI:10.11737/j.issn.1003-0239.2015.05.002 (in Chinese)) |
| [2] |
黄文锋, 周焕林, 孙建鹏. 应用台风风场经验模型的台风极值风速预测[J]. 哈尔滨工业大学学报, 2016, 48(2): 142-146. ( HUANG Wenfeng, ZHOU Huanlin, SUN Jianpeng. Prediction typhoon design wind speed with empirical typhoon wind field model[J]. Journal of Harbin Institute of Technology, 2016, 48(2): 142-146. DOI:10.11918/j.issn.0367-6234.2016.02.024 (in Chinese)) |
| [3] |
张志旭, 齐义泉, 施平, 等. 最优化插值同化方法在预报南海台风浪中的应用[J]. 热带海洋学报, 2003, 22(4): 34-41. ( ZHANG Zhixu, QI Yiquan, SHI Ping, et al. Application of an optimal interpolation wave assimilation method in South China Sea[J]. Journal of Tropical Oceanography, 2003, 22(4): 34-41. (in Chinese)) |
| [4] |
梁连松, 李瑞杰, 丰青, 等. 舟山海域台风浪数值模拟[J]. 水道港口, 2014, 35(6): 582-588. ( LIANG Liansong, LI Ruijie, FENG Qing, et al. Numerical simulation of typhoon wave in Zhoushan[J]. Journal of Waterway and Harbor, 2014, 35(6): 582-588. (in Chinese)) |
| [5] |
齐庆辉, 朱志夏, 王志国, 等. "达维"台风作用下连云港海域台风浪数值模拟[J]. 水利水运工程学报, 2015(5): 60-66. ( QI Qinghui, ZHU Zhixia, WANG Zhiguo, et al. Numerical simulation of storm surge induced by typhoon Dawei in Lianyungang seas[J]. Hydro-Science and Engineering, 2015(5): 60-66. (in Chinese)) |
| [6] |
何倩倩, 杨娟, 王卫远. 台风"达维"影响期间江苏海域台风浪研究[J]. 海洋通报, 2015, 34(5): 592-599. ( HE Qianqian, YANG Juan, WANG Weiyuan. Study on the simulated typhoon waves off Jiangsu coast during Typhoon Damrey[J]. Marine Science Bulletin, 2015, 34(5): 592-599. DOI:10.11840/j.issn.1001-6392.2015.05.014 (in Chinese)) |
| [7] |
金罗斌, 陈国平, 赵红军, 等. 合成风场在南海台风浪数值模拟中的研究[J]. 水道港口, 2015, 36(1): 12-20. ( JIN Luobin, CHEN Guoping, ZHAO Hongjun, et al. Study of combined wind in simulating storm waves in the South China Sea[J]. Journal of Waterway and Harbor, 2015, 36(1): 12-20. (in Chinese)) |
| [8] |
HOLLAND G. An analytic model of the wind and pressure profiles in hurricanes[J]. Monthly Weather Review, 1980, 108(8): 1212-1218. DOI:10.1175/1520-0493(1980)108<1212:AAMOTW>2.0.CO;2 |
| [9] |
HUBBERT G D, HOLLAND G J, LESLIE L M, et al. A real-time system for forecasting tropical cyclone storm surges[J]. Weather and Forecasting, 1991, 6(1): 86-97. DOI:10.1175/1520-0434(1991)006<0086:ARTSFF>2.0.CO;2 |
| [10] |
HOLLAND G. A revised hurricane pressure-wind model[J]. Monthly Weather Review, 2008, 136(9): 3432-3445. DOI:10.1175/2008MWR2395.1 |
| [11] |
WILLOUGHBY H E, RAHN M E. Parametric representation of the primary hurricane vortex. Part Ⅰ: Observations and evaluation of the Holland (1980) model[J]. Monthly Weather Review, 2004, 132(12): 3033-3048. DOI:10.1175/MWR2831.1 |
| [12] |
VICKERY P J, SKERLJ P F, STECKLEY A C, et al. Hurricane wind field model for use in hurricane simulations[J]. Journal of Structural Engineering, 2000, 126(10): 1203-1221. DOI:10.1061/(ASCE)0733-9445(2000)126:10(1203) |
| [13] |
武海浪, 陈希, 陈徐均, 等. 近岸港口风暴潮与台风浪相互作用的数值模拟[J]. 解放军理工大学学报(自然科学版), 2015, 16(4): 360-367. ( WU Hailang, CHEN Xi, CHEN Xujun, et al. Numerical simulation of interaction of storm surge and typhoon wave on near shore harbor[J]. Journal of PLA University of Science and Technology(Natural Science Edition), 2015, 16(4): 360-367. (in Chinese)) |
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Key Laboratory of Engineering Oceanography, Second Institute of Oceanography, State Oceanic Administration, Hangzhou 310012, China;
4. College of Ocean and Meteorology, Guangdong Ocean University, Zhanjiang 524088, China
 2017
2017 