丁坝坝头冲刷坑的变化趋势直接影响丁坝的稳定性,预测冲刷坑变化倍受关注。国内学者[1-6]采用水力模型试验方法,建立了丁坝局部最大冲深的计算公式,并且探究挑角、床沙粒度对冲刷坑形态、位置、尺寸的影响。Pandey等[7-8]通过模型试验得到冲刷深度与弗劳德数的关系以及不同混合沙对坝头及坝下游冲刷深度的影响,Karami等[9]通过水槽试验分析丁坝对主流束窄的影响。佘俊华等[10-12]采用Flow-3D二维泥沙数值模型,计算冲刷坑范围及深度。Gu等[13]采用CFD软件对丁坝群附近的水流进行模拟,认为LES湍流模型能更好地模拟丁坝附近的流场。
已有研究建立的丁坝局部冲刷深度公式反映的是极限状态,不能反映演变趋势;数学模型研究丁坝局部冲刷坑演变趋势尚不成熟。丁坝局部冲刷坑演变是一个复杂的非线性动态系统问题。人工神经网络具有自组织、自学习和非线性逼近的能力,适用于研究非线性问题,近年来取得了长足进展,在水科学等诸多领域得到应用[14-15]。因此,本文探讨采用人工神经网络方法预测丁坝坝头冲刷坑的演变趋势。
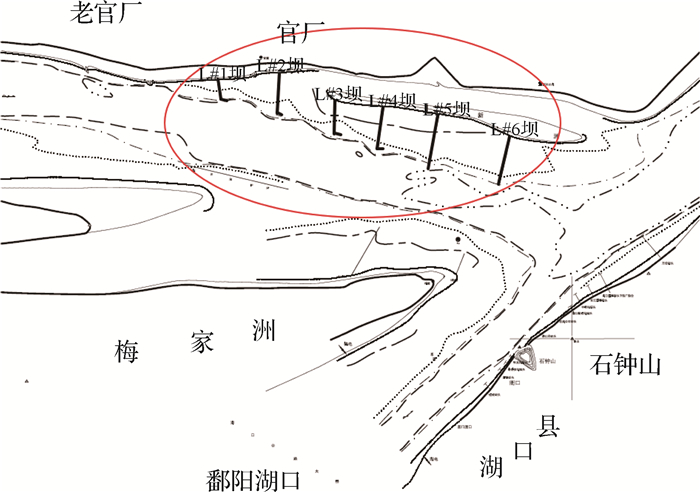
1 研究区域概况张家洲水道为微弯分汊河型,研究河段为张家洲水道南港下浅区(见图 1),航道整治工程包括:左岸6道丁坝,右岸梅家洲边滩建护滩带两道和右岸官洲尾滩缘护岸(护岸长1 090 m)。由于5#和6#丁坝在2008年发生人工非法采砂,同时2010年进行了维修,人为因素影响大,因此本文研究丁坝坝头冲刷坑变化时,仅对1#~4#丁坝开展研究,见表 1。
|
图 1 张家洲水道南港下浅区工程平面布置 Fig.1 Plan layout of the lower shallow area of Zhangjiazhou Waterway |
| 表 1 张南水道1#~4#丁坝参数 Tab.1 Parameters of 1#~4# spur of Zhangnan Waterway |
张家洲水道上游约2.3 km处设有九江水文站,与张家洲水道之间无大的支流入汇,其水文特征值能够反映该水道水文泥沙特性。本文收集了2008—2016年九江站的逐日平均流量、逐日平均输沙量、逐日平均含沙量、逐日平均水位资料,以及张家洲水道南港航道测图及丁坝的高程测图。
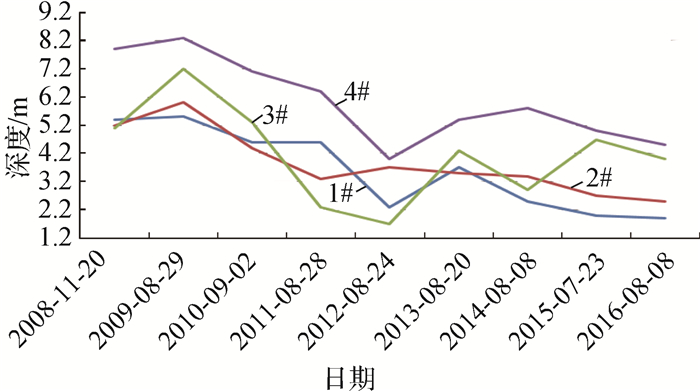
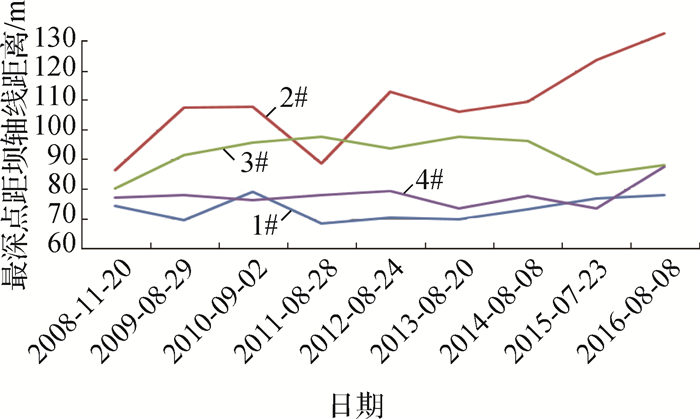
2 影响冲刷坑演变的因素分析 2.1 来水、来沙总量图 2和3为2008—2016年1#~4#丁坝坝头的冲刷坑深度以及最深点距坝轴线距离的变化(每年测1次)。从图 2和3可知,4个丁坝坝头的冲刷坑深度、最深点距坝轴线距离在不同年份的变化趋势大致相同。因此,本文以1#丁坝为例,分析年径流量和年输沙量对冲刷深度以及冲刷坑位置的影响,如图 4和5所示。
|
图 2 2008—2016年1#~4#丁坝冲刷坑深度变化 Fig.2 Change of scouring depth of 1# ~ 4# pits from 2008 to 2016 |
|
图 3 2008—2016年1#~4#冲刷坑最深点位置变化 Fig.3 Change of deepest point position of 1#~4# scouring pits from 2008 to 2016 |
|
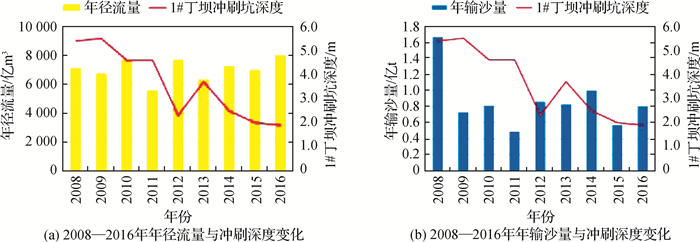
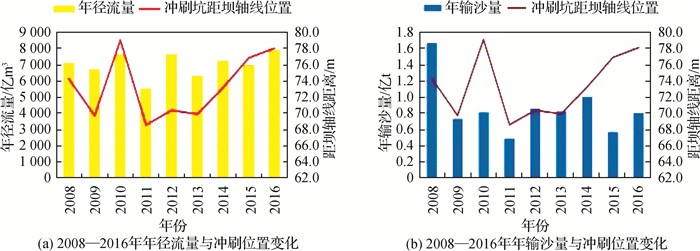
图 4 2008—2016年年径流量、年输沙量与1#丁坝冲刷深度变化 Fig.4 Changes of annual runoff, annual sediment transport volume and scouring depth of 1# spur from 2008 to 2016 |
|
图 5 2008—2016年年径流量、年输沙量与1#丁坝冲刷位置变化 Fig.5 Changes of annual runoff, annual sediment transport volume and scouring position of 1# spur from 2008 to 2016 |
从图 4和5可见,年径流量和年输沙量相对较大的年份,冲刷坑深度大,距坝轴线较近(2008年);年径流量相对较小,年输沙量较大的年份,冲刷坑深度较小,距坝轴线较远(2014年);年径流量较大,年输沙量较小年份,冲刷坑深度较大,距坝轴线较近(2009年)。但是,2012年年径流量和年输沙量较上年增大,冲刷坑深度却减少,最深点与坝轴线距离也增大。这说明丁坝冲刷坑深度以及距坝轴线距离与年径流量和年输沙量并不是单调增或减的关系,而是一个复杂的非线性关系。
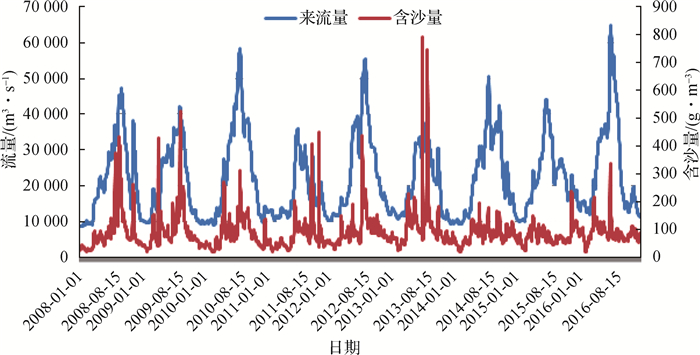
2.2 来水、来沙过程河段上游年来水来沙总量变化不大,但冲刷坑变化有些年份显著不同,这与来水来沙过程有关。九江站2008—2016年实测来水来沙过程变化见图 6,按洪、中、枯划分,枯水期11月至翌年2月的逐日平均流量为10 000~15 000 m3/s,逐日平均含沙量为0~60 g/m3;平水期3—5月及10—11月的逐日平均流量为15 000~25 000 m3/s,逐日平均含沙量为60~100 g/m3;洪水期6—9月逐日平均流量为25 000~40 000 m3/s,逐日平均含沙量为100~250 g/m3。为了反映来水、来沙非恒定过程与冲刷坑变化的关系,本文分级统计逐日平均流量及含沙量的持续天数作为反映来水来沙过程变化的参数。以2010年和2012年为例分级统计逐日平均流量及含沙量的持续天数(见表 2)。2010年和2012年径流量和总输沙量相似,但是两年的各级流量和含沙量持续时间不同,两年冲刷坑的冲刷幅度不一样。说明冲刷坑的变化与来水来沙过程有关。
|
图 6 九江水文站2008—2016年日均流量含沙量过程 Fig.6 Process of daily average flow and sediment concentration in Jiujiang hydrological station from 2008 to 2016 |
| 表 2 2010和2012年逐日平均流量及含沙量持续天数 Tab.2 Daily average flow and sediment concentration in 2010 and 2012 |
丁坝长度直接改变河道有效过水断面的宽度和坝头附近的水流状态,影响坝头冲刷的深度及冲刷坑位置。丁坝挑角可对水流结构及坝后淤积效果产生影响,水槽试验[6]表明,丁坝挑角对淹没丁坝坝头附近床面冲刷坑尺寸、位置以及冲刷坑的变化过程都有一定的影响。
丁坝间的掩护影响需要视实际情况而定。张南水道下浅区左岸6个丁坝组成的丁坝群,1#~4#坝头高程3 m,为等高丁坝群;4#~6#坝头高程分别为3, 2和1 m,为阶梯降丁坝群。5#和6#丁坝高程低于1#~4#丁坝,壅水对1#~4#丁坝冲刷坑的影响较小,可以忽略不计。根据文献[2-3]枯水期丁坝处于非淹没状态,坝头冲刷坑不明显,洪水期洪峰来临丁坝处于淹没状态,冲刷坑大。长江洪季淹没水深大,此时丁坝间的掩护作用可以忽略不计。因此,本文不考虑丁坝间的掩护影响。
河床边界对冲刷坑大小和位置的影响比较复杂,反映河床特征因素有河道宽度、行近水深、床沙中值粒径及泥沙级配等[16],其中关于粒径、泥沙不均匀性与冲刷坑的关系研究成果不一,存在争论。
3 预测模型构建 3.1 输入输出因子根据前文分析可知,丁坝冲刷坑的形成及演变是坝体属性、河床边界条件、水流、泥沙之间相互影响和作用的结果,因此选择下列因素作为输入因子。
坝体属性因子:根据坝体属性与冲刷坑演变间的关系,坝体属性因子取丁坝长度(b)和丁坝挑角(α)。
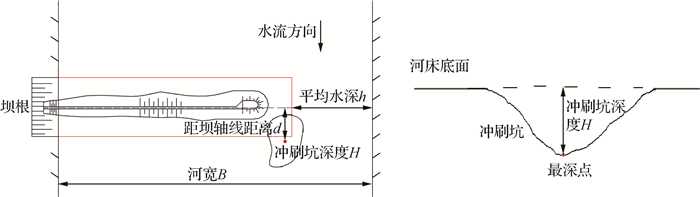
河床边界因子:研究河段2008—2016年间泥沙组成及中值粒径基本稳定,预测冲刷坑变化可暂不考虑河床泥沙组成及粒径的影响。因此,河床边界因子为坝头至河对岸的平均水深(h)、丁坝所在位置河道两岸垂直于水流方向的宽度(B),见图 7。
|
图 7 坝头冲刷坑几何尺度 Fig.7 Schematic diagram of geometrical scale of scouring pit near spur head |
水流、泥沙因子:从前文分析可知,冲刷坑的变化趋势与来水来沙总量及过程关系密切,因此,水流、泥沙因子取来水来沙总量及来水来沙过程,其中,反映来水来沙总量的因子是年径流量(Q)和年输沙量(G);反映来水过程变化影响的因子是各级流量持续的天数TQ1,TQ2,TQ3和TQ4;反映来沙过程变化影响的因子是各级输沙量持续的天数TS1,TS2,TS3和TS4。
输入因子独立性检验采用皮尔逊相关系数法,河床边界条件及坝体属性与来水来沙各因素之间的皮尔逊系数均小于0.3,基本不相关,故输入因子具有独立性。
输出因子为冲刷坑深度(H)以及最深点距坝轴线距离(d)。
3.2 网络建立经过大量试算,本文采用的BP神经网络模型为3层结构14×60×2。“试错法”确定最佳的隐含层节点数n=60时模型预测精度较高。
初始权值随机取值,其值均接近于零,可有效避免计算过早进入饱和区。经反复试验,本文取初始权值在(-1,1)之间的随机数,学习率η=0.01。
4 模型训练与验证为了方便处理计算结果,防止神经元进入过饱和状态,对输入及输出因子进行了规范化处理。样本数据分为两部分:28组数据是训练样本,用于网络的结构学习和权值训练;4组数据是检验样本(见表 3)。在研究时段内,包含了不同情况下的来水来沙条件,2008年为丰水丰沙年,2009年为中水中沙年、2011年为小水少沙年,2012年为丰水中沙年,因此该时段的样本覆盖性较好,基本涵盖各种水文情况,训练样本从水文条件的变化来看具有普遍性。
| 表 3 2015年张南水道1#~4#丁坝检验样本 Tab.3 Inspection sample of 1#~4# spurs of Zhangnan Waterway in 2015 |
由训练样本得到的丁坝坝头附近冲刷坑深度的模拟值与真实值较为吻合,最大误差为6.4%,最小误差为0.1%,平均误差为2.3%;最深点距坝轴线距离的模拟值与真实值较吻合,最大误差为1.3%,最小误差为0.2%,平均误差为0.8%。模型训练结果误差小,收敛效果好。
表 4为模型验证结果,冲刷坑深度预测值的最大绝对误差0.1 m,最小绝对误差-0.1 m,相对误差范围(2.1~5.0)%;最深点距坝轴线距离预测值的最大绝对误差6.8 m,最小绝对误差1.4 m,相对误差范围(1.8~6.5)%。
| 表 4 2015年BP网络模型预测值与实测值比较 Tab.4 Comparison of predicted and actual values of BP network model in 2015 |
通过分析张南水道附近水文站的水沙年际变化和年内变化,结合前人对丁坝冲刷坑的研究成果,确定了反映丁坝冲刷坑变化趋势的特征量为冲刷坑深度及最深点距坝轴线距离;影响丁坝冲刷坑变化的因子为河宽、水深、丁坝长度、丁坝挑角,以及年径流量、年输沙量、逐日平均流量小于15 000 m3/s,15 000~25 000 m3/s,25 000~40 000 m3/s及大于40 000 m3/s的天数,逐日平均输沙量小于60 g/m3,60~100 g/m3,100~250 g/m3,大于250 g/m3的天数。
从BP神经网络模型的预测结果看,模型对张南水道下浅区1#~4#丁坝冲刷坑的深度以及冲刷坑最深点距坝轴线距离的预测与实测值相吻合,说明该方法用于丁坝冲刷坑的深度和位置预测是可行的。
| [1] |
周银军, 陈立, 桂波, 等. 正挑桩式丁坝壅水特性及其冲刷深度计算模式理论[J]. 四川大学学报(工程科学版), 2009, 41(2): 58-63. ( ZHOU Yinjun, CHEN Li, GUI Bo, et al. Theoretical study on calculation of scouring depth and backwater height associated with pile permeable spur dike[J]. Journal of Sichuan University (Engineering Science Edition), 2009, 41(2): 58-63. (in Chinese)) |
| [2] |
张秀芳.非恒定流作用下丁坝水毁试验研究[D].重庆: 重庆交通大学, 2012. (ZHANG Xiufang. Experimental study on the failures of spur dike under unsteady flow[D]. Chongqing: Chongqing Jiaotong University, 2012. (in Chinese)) http://cdmd.cnki.com.cn/Article/CDMD-10618-1013374668.htm
|
| [3] |
喻涛, 王平义, 陈里, 等. 非恒定流作用下丁坝局部冲刷研究[J]. 四川大学学报(工程科学版), 2014, 46(3): 31-36. ( YU Tao, WANG Pingyi, CHEN Li, et al. Local scour of spur dike in unsteady flow[J]. Journal of Sichuan University (Engineering Science Edition), 2014, 46(3): 31-36. (in Chinese)) |
| [4] |
钱撼, 郭志学, 苏杨中. 堆积体作用下的河道最大冲刷深度[J]. 泥沙研究, 2013(3): 65-70. ( QIAN Han, GUO Zhixue, SU Yangzhong. Maximum scour depth under action of deposit body[J]. Journal of Sediment Research, 2013(3): 65-70. DOI:10.3969/j.issn.0468-155X.2013.03.012 (in Chinese)) |
| [5] |
刘磊, 苗润泽, 钟德钰. 细沙河床丁坝局部冲刷深度计算公式的验证[J]. 水力发电学报, 2014, 33(2): 122-130. ( LIU Lei, MIAO Runze, ZHONG Deyu. Verification of calculation formulas for local scour depth of fine sediment riverbed around spur dikes[J]. Journal of Hydroelectric Engineering, 2014, 33(2): 122-130. (in Chinese)) |
| [6] |
陆晶, 倪丁凡, 刘亚威, 等. 挑角对淹没丁坝附近河床变形影响的试验[J]. 武汉大学学报(工学版), 2015, 48(1): 11-14. ( LU Jing, NI Dingfan, LIU Yawei, et al. Experimental study of effects of spur-dike angle on local river bed deformation near a submerged spur-dike[J]. Engineering Journal of Wuhan University, 2015, 48(1): 11-14. (in Chinese)) |
| [7] |
PANDEY M, AHMAD Z, SHARMA P K. Estimation of maximum scour depth near a spur dike[J]. Canadian Journal of Civil Engineering, 2016, 43(3): 270-278. DOI:10.1139/cjce-2015-0280 |
| [8] |
LODHI A S, JAIN R K, SHARMA P K. Influence of cohesion on scour around submerged dike founded in clay-sand-gravel mixtures[J]. ISH Journal of Hydraulic Engineering, 2016, 22(1): 70-87. DOI:10.1080/09715010.2015.1075916 |
| [9] |
KARAMI H, BASSER H, ARDESHIR A, et al. Verification of numerical study of scour around spur dikes using experimental data[J]. Water and Environment Journal, 2014, 28(1): 124-134. DOI:10.1111/wej.12019 |
| [10] |
佘俊华, 夏云峰, 徐华, 等. 护底条件下淹没丁坝坝头局部冲刷试验[J]. 水科学进展, 2016, 27(4): 579-585. ( SHE Junhua, XIA Yunfeng, XU Hua, et al. Experimental study on local scouring of submerged spur dike head under bottom protection condition[J]. Advances in Water Science, 2016, 27(4): 579-585. (in Chinese)) |
| [11] |
孙志林, 倪晓静, 许丹. 丁坝周围流动图像与局部冲刷深度[J]. 浙江大学学报(工学版), 2017, 51(11): 2189-2196. ( SUN Zhilin, NI Xiaojing, XU Dan. Physics of flow and local scour depth around spur dikes[J]. Journal of Zhejiang University (Engineering Science), 2017, 51(11): 2189-2196. DOI:10.3785/j.issn.1008-973X.2017.11.013 (in Chinese)) |
| [12] |
宁健, 李国栋, 马淼. 丁坝绕流流场及局部冲刷三维数值模拟研究[J]. 水动力学研究与进展, 2017, 32(1): 46-53. ( NING Jian, LI Guodong, MA Miao. 3D numerical simulation for flow and local scour around spur dike[J]. Chinese Journal of Hydrodynamics, 2017, 32(1): 46-53. (in Chinese)) |
| [13] |
GU Z H, CAO X M, JIAO Y T, et al. Appropriate CFD models for simulating flow around spur dike group along urban riverways[J]. Water Resources Management, 2016, 30(13): 4559-4570. DOI:10.1007/s11269-016-1436-1 |
| [14] |
任磊, 岳春芳, 何训江. RBF神经网络模型在金沟河流域径流预测中的应用[J]. 水资源与水工程学报, 2011, 22(1): 94-97. ( REN Lei, YUE Chunfang, HE Xunjiang. Application of RBF neural network model to the prediction of runoff in Jingouhe River Basin[J]. Journal of Water Resources and Water Engineering, 2011, 22(1): 94-97. (in Chinese)) |
| [15] |
刘佩瑶, 郝振纯, 王国庆, 等. 新安江模型和改进BP神经网络模型在闽江水文预报中的应用[J]. 水资源与水工程学报, 2017, 28(1): 40-44. ( LIU Peiyao, HAO Zhenchun, WANG Guoqing, et al. Application of Xin'anjiang model and the improved BP neural network model in hydrological forecasting of the Min River[J]. Journal of Water Resources & Water Engineering, 2017, 28(1): 40-44. (in Chinese)) |
| [16] |
周哲宇, 陶东良, 哈岸英, 等. 丁坝局部冲刷研究现状与展望[J]. 人民黄河, 2010, 32(6): 18-21. ( ZHOU Zheyu, TAO Dongliang, HA Anying, et al. Present status and prospects of study on local scour of groins[J]. Yellow River, 2010, 32(6): 18-21. DOI:10.3969/j.issn.1000-1379.2010.06.009 (in Chinese)) |
 2019
2019 
