2. 中国电建集团成都勘测设计研究院有限公司,四川 成都 610072;
3. 中广核工程有限公司 核电安全监控技术与装备国家重点实验室,广东 深圳 518024
地基液化引起的结构破坏在地震中屡有发生,也一直是岩土工程领域的热点问题。相比模型试验方法,数值方法因其具有高效、易于实施、成本低廉等优点,且可以求解具有高度非线性本构关系和复杂初始、边界条件的实际问题,是评价液化问题的主要手段之一。例如,刘华北等[1]和王刚等[2]应用有限元法研究液化地基中地铁车站反应;邹德高等[3]和孔宪京等[4]对液化地基中管线上浮问题进行了研究;黄雨等[5]应用FEM-FDM耦合法研究了液化地基上堤防的动力反应;刘汉龙等[6]对阪神地震中码头岸壁震害进行了数值模拟分析。但只有验证了数值方法的可靠性,应用于工程研究得到结果才具有可信性。将数值解与离心机模型试验数据进行对比是验证液化数值分析方法可靠性的一个重要途径。
20世纪90年代,美国国家科学基金会资助了一项名为VELACS的离心机模型试验计划,目的在于对已有的数值工具和本构模型对于液化问题的分析能力进行验证。国内外很多学者对该计划中的离心机模型试验进行了数值模拟[7-9]。随后二十多年,传感器等试验设备和液化分析方法以及液化土的本构模型均有很大的发展。最近,来自6个国家和地区的科研人员在液化试验与分析计划(LEAP)中开展了一项液化试验,他们分别对同一个饱和斜坡地基进行了离心机模型试验[10-12],为液化数值分析提供了高质量的对比数据。
本文采用大连理工大学改进广义塑性模型[13-16]模拟土体在循环荷载作用下的本构关系,该模型可以考虑土体的剪缩和剪胀特性,进而反映饱和砂土在地震等复杂循环荷载下的液化及循环活动性。在此基础上,应用基于u-p形式的Biot动力固结方程的非线性有限元程序GEODYNA[17-19]模拟了LEAP中饱和斜坡地基离心机试验的动力反应,对比了数值分析和离心机试验得到的地基加速度响应、孔压时程和累积变形等规律,验证了数值方法的可靠性。
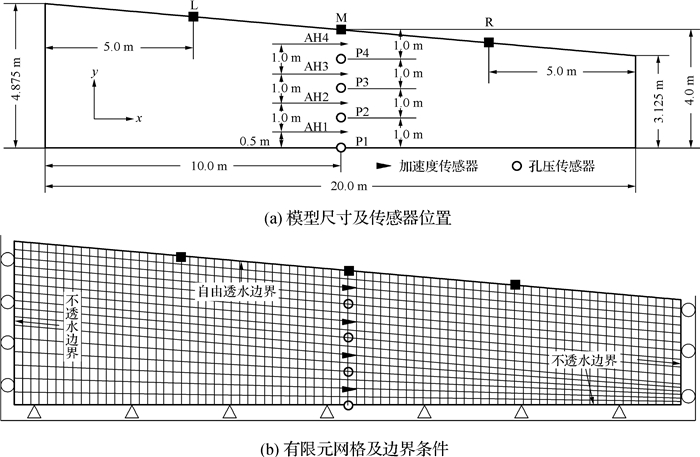
1 离心机模型试验LEAP是一项旨在为液化数值方法提供可靠验证数据的试验分析项目[10],由剑桥大学(CU)、京都大学(KU)、加州大学戴维斯分校(UCD)、国立中央大学(NCU)、伦斯勒理工(RPI)和浙江大学(ZJU)共6所科研机构参与。各参与机构分别对同一个饱和斜坡地基的振动液化问题进行离心机模型试验,试验在刚性箱内进行,地基土为Ottawa砂。模型试验对应的原型如图 1(a)所示,斜坡地基宽20 m,坡面倾角5°,斜坡中间位置厚4.0 m,左、右两侧的厚度分别为4.875和3.125 m。图 1(a)中AH1-AH4为加速传感器的布设位置,P1~P4为孔压传感器的布设位置。试验过程中依次输入了5条(Motion 1~5)变幅值正弦波加速度时程(频率均为1 Hz,持时均为16 s),其中Motion 1, 3, 5最大加速度幅值均为0.015g,Motion 2和Motion 4最大幅值分别为0.15g和0.25g。前后两次输入波的时间间隔足够大以确保振动引起的孔压能够完全消散。本文针对正弦波Motion 2输入时斜坡地基的动力响应进行了数值模拟,将数值分析得到的加速度、孔压及变形等结果与离心机试验实测结果[10-12]进行比较。
|
图 1 饱和斜坡地基模型示意 Fig.1 Schematic diagram for the saturated slope ground used in the centrifuge test |
数值分析采用大连理工大学抗震研究所自主开发的非线性有限元程序GEODYNA,该程序基于u-p形式的Biot动力固结方程[20],可以考虑土体和孔隙流体的耦合作用。有限元控制方程可表达为:
| $ \boldsymbol{M} \ddot{\bar{\boldsymbol{u}}}+\boldsymbol{C} \dot{\bar{\boldsymbol{u}}}+\boldsymbol{K} \overline{\boldsymbol{u}}-\boldsymbol{Q} \overline{\boldsymbol{p}}-\boldsymbol{f}^{(1)}=0 $ | (1) |
| $ \boldsymbol{M}_{\rm{f}} \ddot{\bar{\boldsymbol{u}}}+\boldsymbol{Q}^{\mathrm{T}} \dot{\bar{\boldsymbol{u}}}+\boldsymbol{S} \dot{\bar{\boldsymbol{p}}}+\boldsymbol{H} \overline{\boldsymbol{p}}-\boldsymbol{f}^{(2)}=0 $ | (2) |
式中:M为土体的质量矩阵;C为阻尼矩阵;K为刚度矩阵;Q为耦合矩阵;f(1)为土体的荷载向量;Mf为流体的质量矩阵;S为流体的压缩矩阵;H为流体的渗透矩阵;f(2)为流体的荷载向量。采用广义Newmark时域离散法[20]将上述二阶常微分方程组方程组转化为代数方程组进行求解。结合程序内置的大连理工大学改进广义塑性本构模型,可以模拟地震等动力荷载作用下土体内孔压累积、发展和消散以及残余变形的累积。
有限元网格划分首先要考虑到传感器的布设位置,确保在传感器处设有节点,以便于试验数据和数值结果的比较。此外,还要满足波的传播对于网格尺寸的要求,在波的传播方向单元尺寸不大于波长的1/9~1/6[21]。本文有限元网格如图 1(b)所示,采用四边形等参单元,共1 280个单元,1 377个节点,单元横向尺寸为0.25 m,纵向最大尺寸为0.36 m,最小尺寸为0.15 m。模拟刚性箱对斜坡地基的约束作用,边界条件设为:底部节点水平向和竖向约束,左、右两侧边界均为法向约束;地基表面自由透水,底部以及左、右两侧边界均为不透水边界。
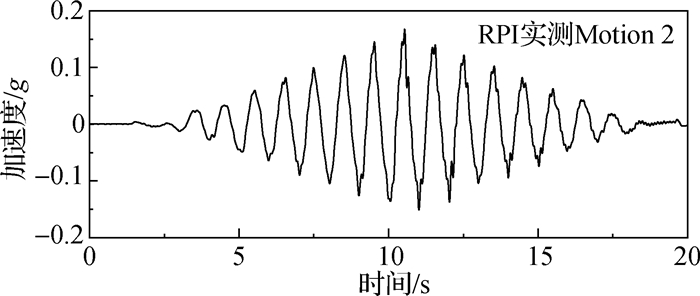
2.2 计算参数根据模型试验中Ottawa砂的三轴试验数据对广义塑性模型参数进行标定,模型参数列于表 1。依据Ottawa砂[22-23]的物理性质试验数据,砂土渗透系数取0.018 cm/s。输入水平向地震波,地震波采用图 2中RPI实测Motion 2加速度时程,计算时间步长取0.005 s。计算时,除了广义塑性模型的滞回效应外,还引入瑞利阻尼确保数值计算的稳定性,阻尼比取0.05。
| 表 1 砂土广义塑性模型参数 Tab.1 Generalized plastic model parameters for the slope ground soil |
|
图 2 输入加速度时程 Fig.2 Input acceleration time history |
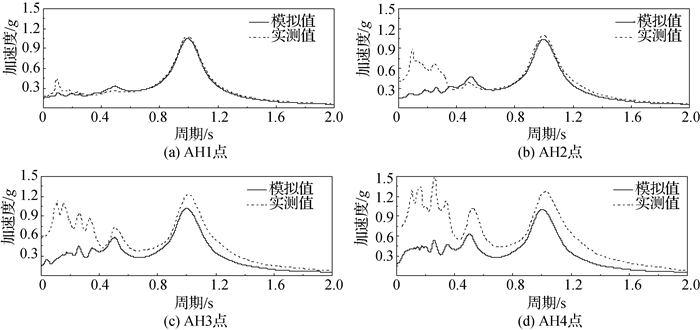
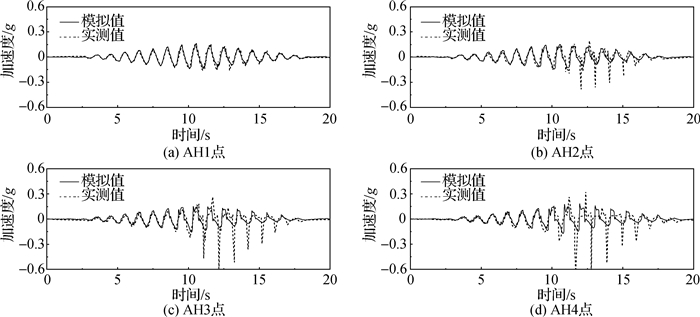
图 3给出了监测点AH1~AH4的加速度反应谱,各监测点的位置如图 1(a)所示。对比数值结果和实测数据,数值模拟基本再现了地基中实际加速度响应。其中,埋深较深的AH1和AH2点,模拟得到的加速度反应谱与实测反应谱基本一致;埋深较浅的AH3和AH4点,模拟值在高频段与实测数据存在偏差,在输入频率1 Hz附近,模拟得到的加速度和实测加速度较为接近,总体上加速反应谱在0~2 s周期内的分布规律与试验数据基本吻合。图 4给出了模拟和实测的AH1~AH4点0~20 s的加速度时程曲线,两者在9 s以前基本一致,但在9 s以后(此时变形和孔压较大)实测加速度在x负方向存在差异。上述反应谱的差异主要是由9 s以后的地震加速度引起的。
|
图 3 实测和模拟加速度反应谱 Fig.3 Comparison between measured and simulated acceleration response spectrum |
|
图 4 加速度时程 Fig.4 Comparison between measured and simulated acceleration time histories |
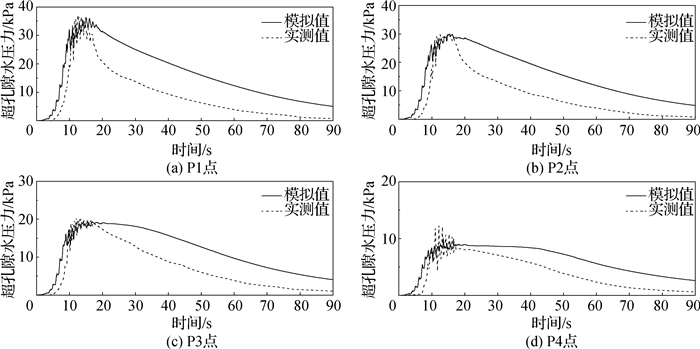
模型中线处点P1~P4的超孔隙水压力模拟值及试验值如图 5所示,图中给出了各点0~90 s的孔压,包括振动过程中孔压的累积上升阶段和振动结束后孔压的消散阶段。经比较,数值计算得到的孔压累积和消散趋势以及数值大小与试验实测值较为接近。振动开始阶段输入的正弦波幅值较小,在地基中没有引起明显的孔压,随着输入波幅值的增大,土体的塑性体变显著增加,地基内的孔隙水压力开始迅速累积上升,逐渐接近初始竖向有效应力。
|
图 5 实测和模拟超孔压时程 Fig.5 Comparison between measured and simulated excess pore pressure time histories |
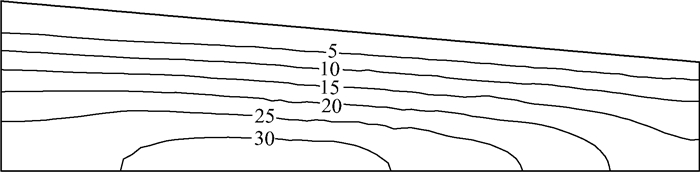
图 6给出了20 s时斜坡地基内超孔隙水压力的分布。随着埋深由浅及深,孔隙水压力逐渐增加,其中地基底部中心区域孔压值最大,约为32 kPa。底部测点P1和P2在振动结束后孔压随即开始消散,而顶部节点P3和P4在振动结束后,孔压值没有明显下降,这是由于振动结束后地基底部区域孔隙水压力较大,孔隙水将沿着排水路径由下向上排出,减缓了表层土体孔压减小的速度。
|
图 6 20 s时地基内超孔压分布(单位: kPa) Fig.6 Excess pore pressure distribution of the slope ground at 20 s (unit: kPa) |
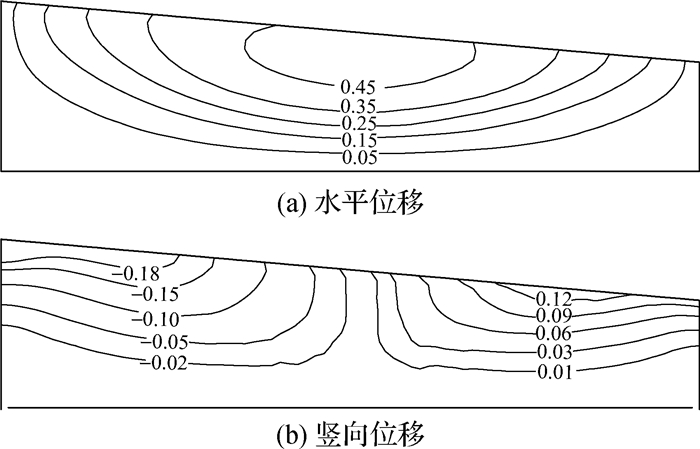
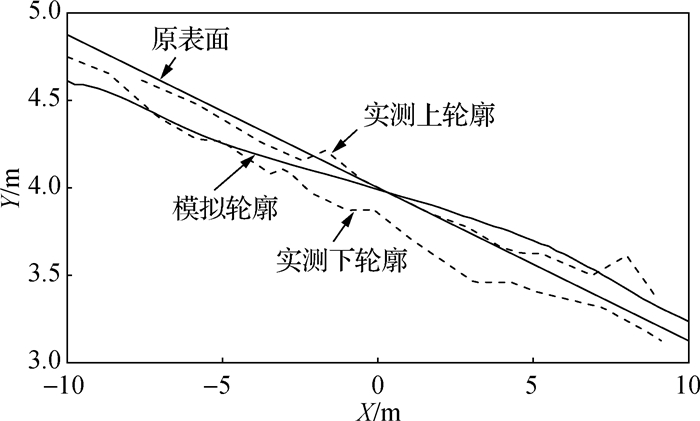
图 7给出了20 s时地基的网格变形图(变形放大3倍),由于斜坡地基存在初始剪应力,地基整体发生向右的侧向变形,地基左半部分产生沉降变形,右半部分则产生隆起变形。图 8分别给出了20 s时地基内水平位移和竖向位移云图,其中水平位移由下到上依次增大,左、右两侧受边界水平位移较小,地基中部水平位移较大,最大值约为0.48 m;左侧地基表面最大沉降值约为0.26 m,右侧地基表面最大隆起值约为0.15 m。在对LEAP试验进行数值分析的一些其他研究[23-25]中也得到了同样的变形分布规律。图 9给出了地基振动结束后地基表面的竖向变形包络图,可以看到模拟规律与试验结果规律一致,且量值基本位于各研究单位试验结果的上、下包络线之间。

|
图 7 20 s时地基3倍变形 Fig.7 Three times deformation of the slope ground at 20 s |
|
图 8 20 s时位移等值线(单位: m) Fig.8 Displacement contour lines of the slope ground at 20 s (unit: m) |
|
图 9 地基表面竖向位移包络图 Fig.9 Envelope diagram of vertical displacement of ground surface |
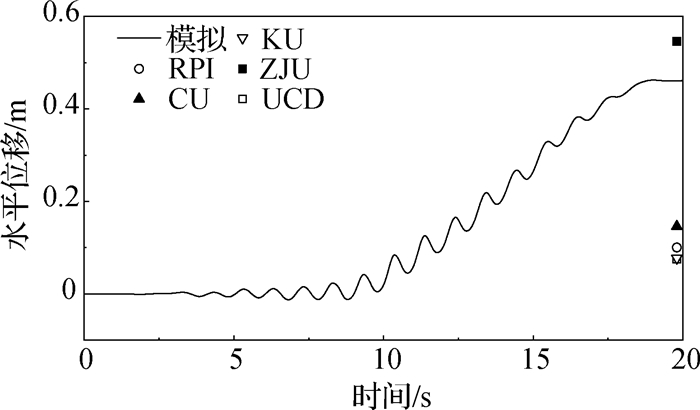
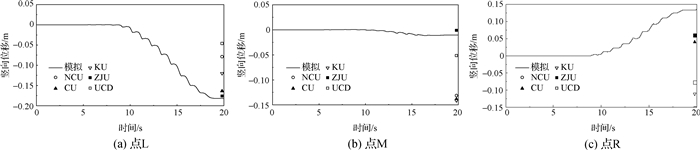
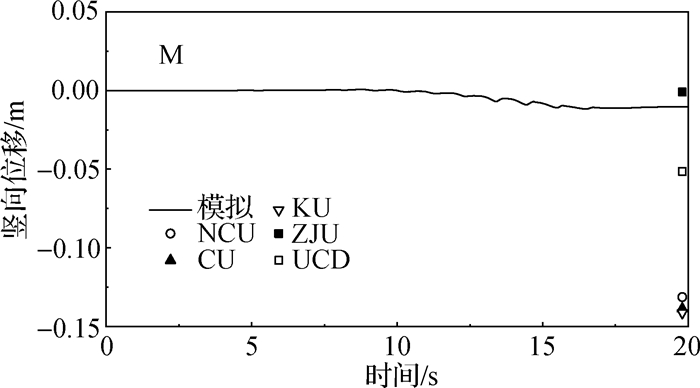
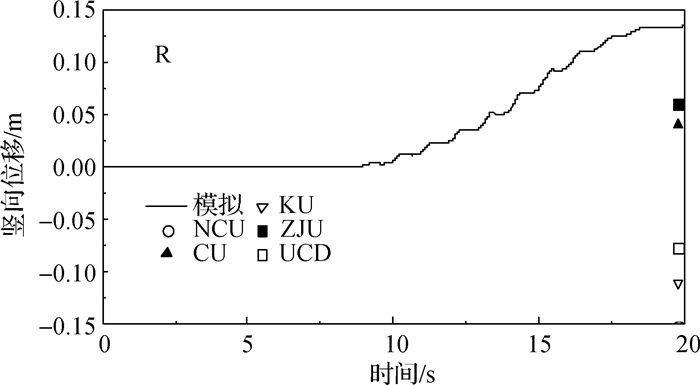
图 10给出了地基表面中点M的水平向位移时程。在振动初期,水平位移以可恢复的弹性变形为主,大约从9 s开始由于孔压逐渐接近竖向压力,导致地基的有效应力显著降低,地基开始产生明显的由左向右的侧向残余变形。图 11给出了地基表面3个点L, M, R的竖向位移时程,可以看到竖向变形发展规律与水平位移规律类似。将模拟值和试验机构实测的最终位移值[10]进行比较,虽然控制条件一致但各单位的位移数据比较离散。中心M点的水平位移数值为0.46 m,与ZJU的结果更接近;左侧点L处沉降值约为0.18 m,与ZJU的结果数据基本一致;右侧点R处向上隆起,20 s时隆起值约为0.13 m,大于所有试验结果;中线处点M也发生沉降,数值较小,与ZJU实测数据接近。
|
图 10 振动阶段表面中点M的水平位移时程 Fig.10 Horizontal displacement time history of surface node M during shaking event |
|
图 11 振动阶段表面竖向位移时程 Fig.11 Vertical displacement history of surface nodes |
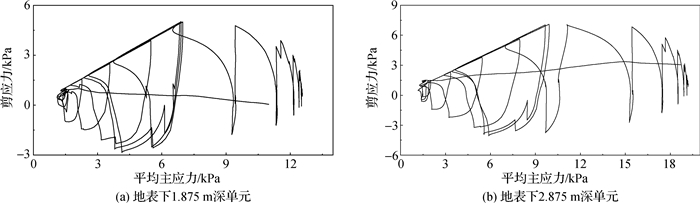
图 12给出了位于模型中线处埋深1.875和2.875 m单元的水平剪应力和平均有效应力之间的关系。从图 12中可以看出,随着振幅和振动时间增加,塑性体变引起土体内孔隙水压力显著升高,导致有效应力迅速降低减小。当剪应力达到一定水平后,随着剪应力增加土体中有效应力增加,呈现出明显的剪胀现象。振动结束后,孔隙水不断固结排出,孔压降低,平均有效应力持续增加。
|
图 12 剪应力τ和平均有效主应力p的关系 Fig.12 Relationship between shear stress τ and mean effective principal stress p |
图 13给出了振动过程地基内最大动剪应力的分布,地基底部的动剪应力较大,表面和两侧边界的动剪应力较小。相应的动剪应力比(最大动剪应力与初始平均有效应力之比)如图 14所示,地基大部分区域动剪应力比都在0.2以上,只有两侧边界附近小范围区域内动剪应力比低于0.2,地基中心区域动剪应力达到0.33以上。
|
图 13 振动过程地基最大动剪应力(单位: kPa) Fig.13 Maximum dynamic shear stress during shaking event (unit: kPa) |
|
图 14 振动过程最大动剪应力比 Fig.14 Dynamic shear stress ratio during shaking event |
应用基于u-p形式的Biot动力固结方程的非线性有限元程序GEODYNA和改进的广义塑性模型对LEAP中的饱和斜坡地基离心机模型试验进行了动力弹塑性有效应力数值分析,并将数值结果与试验数据进行对比。结果表明:
(1)数值模拟得到的地基深层测点的加速度反应谱与实测数据吻合较好,浅层测点除在高频部分存在偏差外也与实测值较为接近;典型节点处的加速度时程和试验规律也较为接近。
(2) 振动过程中超孔隙水压力的上升趋势和振后超孔隙水压力的消散趋势与试验数据基本一致,孔压的大小也与试验数据较为吻合。数值分析可以再现地基液化前、液化和孔压消散阶段土体的应力路径和循环剪切作用下土体的剪胀现象。
(3) 数值模拟和模型试验得到的地表沉降规律基本相符。数值模拟合理地再现了地基典型位置处竖向和侧向变形在振动液化过程的累积过程,振动初始阶段变形以可恢复的弹性变形为主,随着输入振幅的增加,土体刚度显著降低,土体发生明显的侧向和竖向残余变形。
(4) 考虑土水耦合作用的非线性有限元程序GEODYNA和大连理工大学改进的广义塑性模型可以合理再现离心机试验中饱和斜坡地基的动力响应,验证了本文方法的可靠性,为工程实践中饱和土液化安全评价提供了有效、可信的数值工具。
数值模拟与试验数据存在的偏差可能源于地基土与刚性箱边界的简化以及三维模型向二维平面应变模型的简化等。模型边界简化形式的影响、模型维度的影响有待于进一步研究。
| [1] |
刘华北, 宋二祥. 可液化土中地铁结构的地震响应[J]. 岩土力学, 2005, 26(3): 381-386, 391. ( LIU Huabei, SONG Erxiang. Earthquake induced liquefaction response of subway structure in liquefiable soil[J]. Rock and Soil Mechanics, 2005, 26(3): 381-386, 391. DOI:10.3969/j.issn.1000-7598.2005.03.009 (in Chinese)) |
| [2] |
王刚, 张建民, 魏星. 可液化土层中地下车站的地震反应分析[J]. 岩土工程学报, 2011, 33(10): 1623-1627. ( WANG Gang, ZHANG Jianmin, WEI Xing. Seismic response analysis of a subway station in liquefiable soil[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(10): 1623-1627. (in Chinese)) |
| [3] |
邹德高, 孔宪京. 液化土中管线抗上浮排水措施数值分析[J]. 大连理工大学学报, 2010, 50(3): 379-385. ( ZOU Degao, KONG Xianjing. Numerical analysis of mitigation methods against pipeline up-lifting in liquefiable soil[J]. Journal of Dalian University of Technology, 2010, 50(3): 379-385. (in Chinese)) |
| [4] |
孔宪京, 邹德高. 基于液化后变形分析方法的地下管线上浮反应研究[J]. 岩土工程学报, 2007, 29(8): 1199-1204. ( KONG Xianjing, ZOU Degao. Study on uplift behavior of pipelines based on post-liquefaction deformation method[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(8): 1199-1204. DOI:10.3321/j.issn:1000-4548.2007.08.012 (in Chinese)) |
| [5] |
黄雨, 八嵨厚, 沢田和秀, 等. 堤防地基地震液化的数值模拟[J]. 工程力学, 2007, 24(12): 82-87. ( HUANG Yu, YASHIMA A, SAWADA K, et al. Numerical modeling of earthquake liquefaction in earth embankment foundations[J]. Engineering Mechanics, 2007, 24(12): 82-87. DOI:10.3969/j.issn.1000-4750.2007.12.015 (in Chinese)) |
| [6] |
刘汉龙, 井合进, 一井康二. 大型沉箱式码头岸壁地震反应分析[J]. 岩土工程学报, 1998, 20(2): 26-30. ( LIU Hanlong, IAI S, ICHII K. Seismic response analysis of large-size caisson quay wall[J]. Chinese Journal of Geotechnical Engineering, 1998, 20(2): 26-30. DOI:10.3321/j.issn:1000-4548.1998.02.009 (in Chinese)) |
| [7] |
王刚, 张建民. 砂土液化变形的数值模拟[J]. 岩土工程学报, 2007, 29(3): 403-409. ( WANG Gang, ZHANG Jianmin. Numerical modeling of liquefaction-induced deformation in sand[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(3): 403-409. DOI:10.3321/j.issn:1000-4548.2007.03.015 (in Chinese)) |
| [8] |
POPESCU R, PREVOST J H. Centrifuge validation of a numerical model for dynamic soil liquefaction[J]. Soil Dynamics and Earthquake Engineering, 1993, 12(2): 73-90. DOI:10.1016/0267-7261(93)90047-U |
| [9] |
BYRNE P M, PARK S S, BEATY M, et al. Numerical modeling of liquefaction and comparison with centrifuge tests[J]. Canadian Geotechnical Journal, 2004, 41(2): 193-211. DOI:10.1139/t03-088 |
| [10] |
KUTTER B L, CAREY T J, HASHIMOTO T, et al. LEAP-GWU-2015 experiment specifications, results, and comparisons[J]. Soil Dynamics and Earthquake Engineering, 2018, 113: 616-628. DOI:10.1016/j.soildyn.2017.05.018 |
| [11] |
MANZARI M T, EL GHORAIBY M, KUTTER B L, et al. Liquefaction Experiment and Analysis Projects (LEAP): summary of observations from the planning phase[J]. Soil Dynamics and Earthquake Engineering, 2018, 113: 714-743. DOI:10.1016/j.soildyn.2017.05.015 |
| [12] |
KOKKALI P, ABDOUN T, ZEGHAL M. Physical modeling of soil liquefaction: overview of LEAP production test 1 at Rensselaer Polytechnic Institute[J]. Soil Dynamics and Earthquake Engineering, 2018, 113: 629-649. DOI:10.1016/j.soildyn.2017.01.036 |
| [13] |
孔宪京, 邹德高, 徐斌, 等. 紫坪铺面板堆石坝三维有限元弹塑性分析[J]. 水力发电学报, 2013, 32(2): 213-222. ( KONG Xianjing, ZOU Degao, XU Bin, et al. Three-dimensional finite element elasto-plastic analysis of Zipingpu concrete faced rock-fill dam[J]. Journal of Hydroelectric Engineering, 2013, 32(2): 213-222. (in Chinese)) |
| [14] |
邹德高, 杨依民, 刘京茂, 等. 广义塑性模型在海洋砂土中的适用性研究[J]. 水电能源科学, 2013, 31(11): 159-162. ( ZOU Degao, YANG Yimin, LIU Jingmao, et al. Study on adaptability of generalized plastic model in ocean sand[J]. Water Resources and Power, 2013, 31(11): 159-162. (in Chinese)) |
| [15] |
ZOU D G, XU B, KONG X J, et al. Numerical simulation of the seismic response of the Zipingpu concrete face rockfill dam during the Wenchuan earthquake based on a generalized plasticity model[J]. Computers and Geotechnics, 2013, 49: 111-122. DOI:10.1016/j.compgeo.2012.10.010 |
| [16] |
邹德高, 徐斌, 孔宪京, 等. 基于广义塑性模型的高面板堆石坝静、动力分析[J]. 水力发电学报, 2011, 30(6): 109-116. ( ZOU Degao, XU Bin, KONG Xianjing, et al. Static and dynamic analysis of high concrete-faced rockfill dam based on generalized plastic model[J]. Journal of Hydroelectric Engineering, 2011, 30(6): 109-116. (in Chinese)) |
| [17] |
邹德高.地震时浅埋地下管线上浮机理及减灾对策研究[D].大连: 大连理工大学, 2008. (ZOU Degao. Study on uplifting mechanism and mitigation measurement of the pipelines buried at shallow depth during the earthquake[D]. Dalian: Dalian University of Technology, 2008. (in Chinese)) http://cdmd.cnki.com.cn/Article/CDMD-10141-2009040891.htm
|
| [18] |
ZOU D G, TENG X W, CHEN K, et al. An extended polygon scaled boundary finite element method for the nonlinear dynamic analysis of saturated soil[J]. Engineering Analysis with Boundary Elements, 2018, 91: 150-161. DOI:10.1016/j.enganabound.2018.03.019 |
| [19] |
ZOU D G, TENG X W, CHEN K, et al. A polyhedral scaled boundary finite element method for three-dimensional dynamic analysis of saturated porous media[J]. Engineering Analysis with Boundary Elements, 2019, 101: 343-359. DOI:10.1016/j.enganabound.2019.01.012 |
| [20] |
ZIENKIEWICZ O C, CHAN A H C, PASTOR M, et al. Computational geomechanics with special reference to earthquake engineering[M]. Chichester: Wiley, 1999.
|
| [21] |
刘晶波, 廖振鹏. 离散网格中的弹性波动(Ⅱ)——几种有限元离散模型的对比分析[J]. 地震工程与工程振动, 1989, 9(2): 1-11. ( LIU Jingbo, LIAO Zhenpeng. Elastic wave motion in discrete grids (Ⅱ)——Comparison of common finite element models[J]. Earthquake Engineering and Engineering Vibration, 1989, 9(2): 1-11. (in Chinese)) |
| [22] |
VASKO A. An investigation into the behavior of Ottawa sand through monotonic and cyclic shear tests[D]. Washington: The George Washington University, 2015. https://search.proquest.com/docview/1685959360
|
| [23] |
GHOFRANI A, ARDUINO P. Prediction of LEAP centrifuge test results using a pressure-dependent bounding surface constitutive model[J]. Soil Dynamics and Earthquake Engineering, 2018, 113: 758-770. DOI:10.1016/j.soildyn.2016.12.001 |
| [24] |
MADABHUSHI S S C, HAIGH S K, MADABHUSHI G S P. LEAP-GWU-2015: centrifuge and numerical modelling of slope liquefaction at the University of Cambridge[J]. Soil Dynamics and Earthquake Engineering, 2018, 113: 671-681. DOI:10.1016/j.soildyn.2016.11.009 |
| [25] |
ZIOTOPOULOU K. Seismic response of liquefiable sloping ground: class A and C numerical predictions of centrifuge model responses[J]. Soil Dynamics and Earthquake Engineering, 2018, 113: 744-757. DOI:10.1016/j.soildyn.2017.01.038 |
2. Power China Chengdu Engineering Corporation Limited, Chengdu 610072, China;
3. State Key Laboratory of Nuclear Power Safety Monitoring Technology and Equipment, China Nuclear Power Engineering Co., Ltd., Shenzhen 518024, China
 2019
2019 
