2. 中国电建集团贵阳勘测设计研究院有限公司,贵州 贵阳 550081
现代堆石坝坝型主要包括面板堆石坝和心墙堆石坝[1]。一般来说,心墙堆石坝适应坝体变形能力优于面板堆石坝,所以世界范围内,200~300 m级特高土石坝大多为心墙堆石坝,如坝高235 m的美国Oroville坝[2]、坝高261.5 m的糯扎渡心墙堆石坝[3]、坝高242.0 m的加拿大Mica心墙堆石坝[4]以及坝高292 m的两河口心墙堆石坝。我国一批300 m级的心墙堆石坝也正在筹划建设,这些高库大坝设计和建设管理经验相对比较缺乏,数值模拟成为了预测结构性状的有力工具。数值计算旨在尽可能模拟大坝实际情况,但传统土石坝数值模拟认为基岩与坝体模量相差巨大,不考虑地基的变形,坝体固定在基岩上,也无法考虑坝体-地基之间的接触摩擦变形。已有原型观测资料表明,修建在陡峻狭窄河谷区的高土石坝,坝体与地基之间的摩擦效应强烈[5],所以传统模拟方法与实际情况不符。宋文晶等[6]曾采用一种接触摩擦单元模拟了面板堆石坝坝体与坝基的摩擦接触效应,结果表明坝体与地基之间存在明显的滑动位移;文献[7]对狭窄河谷区面板堆石坝坝体-地基接触效应进行了模拟研究,结果表明不考虑接触效应高估了岸坡部位坝体的拱效应;文献[8]提出了一个接触摩擦弹塑性模型用于模拟坝体-地基相对滑移。总体来说目前对坝体-地基接触效应的研究尚不充分,尤其是在湿化、流变等变形共同作用下坝体-地基接触面演化规律的研究极少。本文研究以狭窄河谷区特高心墙坝为例,模拟考虑坝体湿化、流变效应的特高坝坝体应力变形长期演化规律以及坝体-地基接触变形演化规律,以评估狭窄河谷区特高心墙堆石坝结构的长期安全性。
1 计算理论与模型 1.1 计算理论为了模拟心墙堆石坝在填筑和蓄水期孔隙水压力的产生、消散规律,本文研究采用基于Biot固结理论[9]的有效应力有限单元法。Biot固结理论中土骨架和孔隙水之间的相互影响服从有效应力原理,土体平衡方程如式(1)。
| $ \left\{\begin{array}{l} {\frac{\partial \sigma_{x}^{\prime}}{\partial x}+\frac{\partial \tau_{x y}}{\partial y}+\frac{\partial \tau_{x z}}{\partial z}+\frac{\partial p}{\partial x}=0} \\ {\frac{\partial \tau_{y x}}{\partial x}+\frac{\partial \sigma_{y}^{\prime}}{\partial y}+\frac{\partial \tau_{y z}}{\partial z}+\frac{\partial p}{\partial y}=0} \\ {\frac{\partial \tau_{z x}}{\partial x}+\frac{\partial \tau_{z y}}{\partial y}+\frac{\partial \sigma_{z}^{\prime}}{\partial z}+\frac{\partial p}{\partial z}-\rho g=0} \end{array}\right. $ | (1) |
式中:σ′x, σ′y, σ′z, τxy, τyz, τzx为有效应力分量;p为孔隙压力;ρ为土体密度;g为重力加速度。
孔隙水连续性方程表示为:
| $ \frac{\partial \varepsilon_{\mathrm{v}}}{\partial t}=-\frac{1}{\rho_{\mathrm{w}} g}\left(k_{x} \frac{\partial^{2} p}{\partial x^{2}}+k_{y} \frac{\partial^{2} p}{\partial y^{2}}+k_{z} \frac{\partial^{2} p}{\partial z^{2}}\right) $ | (2) |
式中:ρw为孔隙水密度;εv为土体应变;kx, ky, kz为x, y, z三向渗透系数。
采用有限元方法求解Biot固结微分方程,其支配方程为
| $ \left[\begin{array}{cc} {\boldsymbol{K}_{{\rm e}}} & {\boldsymbol{K}_{{\rm c}}} \\ {\boldsymbol{K}_{{\rm c}}{^{\mathrm{T}}}} & {-\theta \Delta t \boldsymbol{K}_{{\rm s}}} \end{array}\right]\left\{\begin{array}{l} {\Delta \boldsymbol{u}} \\ {\Delta \boldsymbol{p}} \end{array}\right\}=\left\{\begin{array}{l} {\Delta R} \\ {\Delta t\left(\boldsymbol{R}_{\mathrm{q}}+\boldsymbol{K}_{\rm s} \boldsymbol{p}_{n}\right)} \end{array}\right\} $ | (3) |
式中:Ke为土骨架刚度矩阵;Ks为渗透矩阵;Kc为耦合矩阵;Δu为结点位移增量;Δp为结点孔压增量;ΔR为结点荷载增量;Rq为等效结点流量;θ为结点积分常数;pn为tn时刻结点孔压。
1.2 筑坝料本构模型 1.2.1 瞬变模型筑坝料瞬变模型采用土石坝工程中常用的邓肯E-B模型,切线弹性模量Et如式(4),切线体积模量Bt如式(5)。
| $ E_{\mathrm{t}}=K \cdot p_{\mathrm{a}} \cdot\left(\frac{\sigma_{3}}{p_{\mathrm{a}}}\right)^{n}\left(1-R_{\mathrm{f}} \cdot S_{{\rm l}}\right)^{2} $ | (4) |
| $ B_{\mathrm{t}}=K_{\mathrm{b}} \cdot p_{\mathrm{a}} \cdot\left(\frac{\sigma_{3}}{p_{\mathrm{a}}}\right)^{m} $ | (5) |
式中:K, n, Rf, Kb, m为材料参数;σ3为第三主应力;Sl为剪应力水平;pa为大气压力。
1.2.2 流变模型为了模拟应力作用下筑坝料变形随时间变化的特性,本研究采用李国英等[10]提出的7参数流变模型,如式(6)。
| $ \left.\begin{array}{rl} {\varepsilon_{\mathrm{vf}}} & {=b\left(\frac{\sigma_{3}}{p_{\mathrm{a}}}\right)^{m_{1}}+c\left(\frac{q}{p_{\mathrm{a}}}\right)^{m_{2}}} \\ {\gamma_{\mathrm{f}}} & {=d\left(\frac{S_{{\rm l}}}{1-S_{{\rm l}}}\right)^{m_{3}}} \end{array}\right\} $ | (6) |
式中:εvf为最终体积流变;γf为最终剪切流变;q为广义剪应力;b,c,d,m1,m2,m3为模型参数,流变变形的发展过程可用指数型函数描述,如式(7)。
| $ \varepsilon(t)=\varepsilon_{\mathrm{f}}(1-\exp (-\alpha t)) $ | (7) |
式中:α为表征流变变形发展的参数。
1.2.3 湿化模型湿化模型用于模拟筑坝料在蓄水过程中由非饱和状态转变为饱和状态时发生的湿陷变形,本次研究采用沈珠江提出的3参数湿化变形模型,湿化体积变形εvs和湿化剪切变形Δγ可表示为:
| $ \varepsilon_{\mathrm{vs}}=c_{\mathrm{w}}\left(\frac{\sigma_{3}}{p_{\mathrm{a}}}\right)^{n_{\mathrm{w}}} $ | (8) |
| $ \Delta \gamma=b_{\mathrm{w}} \frac{S_{1}}{1-S_{1}} $ | (9) |
式中:cw,nw,bw为材料参数。
1.3 坝体-地基接触面模型坝体-地基接触模拟采用无厚度的Goodman模型[11],接触面剪切切线刚度形式如下:
| $ K_{\mathrm{t}}=k_{1} \cdot \gamma_{\mathrm{w}}\left(\frac{\sigma_{\mathrm{n}}}{p_{\mathrm{a}}}\right)^{n}\left(1-\frac{R_{\mathrm{f}} \tau}{C+\sigma_{\mathrm{n}} \operatorname{tg} \varphi}\right)^{2} $ | (10) |
式中:k1, n, Rf为材料参数;γw为水的重度;σn为法向应力; τ为剪应力; C和φ为咬合强度与摩擦角。
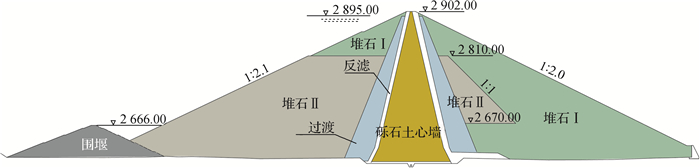
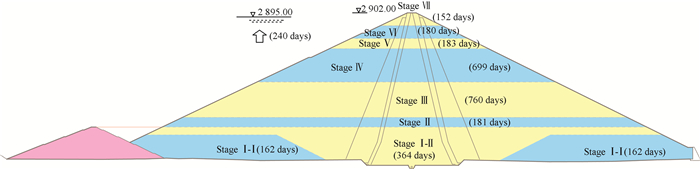
1.4 如美堆石坝有限元数值模型高315 m的如美特高心墙堆石坝典型剖面分区如图 1,坝料主要包括堆石Ⅰ、堆石Ⅱ、过渡、反滤、砾石心墙土、接触黏土等,填筑分为7期,共2 681 d(图 2),大坝填筑至顶后开始蓄水,蓄水至正常蓄水位2 895.0 m高程共用240 d,运行期模拟至大坝蓄水运行后8年。
|
图 1 如美心墙堆石坝典型材料分区(单位:m) Fig.1 Maximum cross section of the Rumei earth-core rockfill dam (unit: m) |
|
图 2 如美心墙堆石坝填筑蓄水过程(单位:m) Fig.2 Construction schedule of the Rumei earth-core rockfill dam (unit: m) |
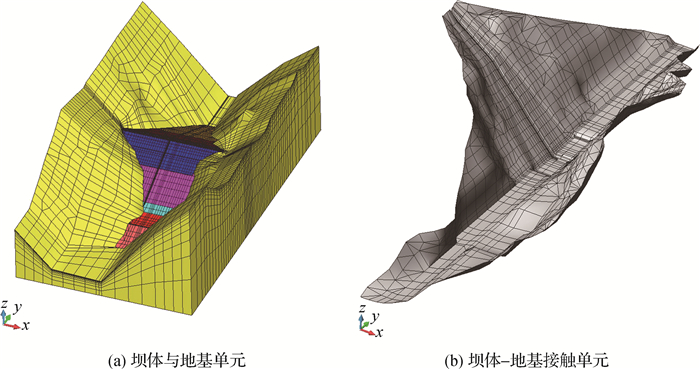
大坝有限元网格离散如图 3,有限元模型包括了坝体及地基,坝体与地基接触采用无厚度接触摩擦单元模拟[12],如图 3(b)。有限元模型共包含节点59 061个,单元62 262个,数值模型严格按照坝体实际填筑加载过程进行模拟(图 2),坝体填筑、蓄水、运行共采用了95个荷载级进行模拟。筑坝料邓肯E-B模型参数见表 1,坝料流变和湿化模型参数见表 2。坝料与基岩之间接触面参数取值如下:堆石料与基岩,φ=31.9°, C=0.178 MPa, k1=6 747,法向刚度K2=108 kN/m3(受压),法向刚度K2=5 kN/m3(受拉),n=0.62, Rf=0.85;接触黏土与混凝土垫层,φ=22.0°, C=0.040 MPa, k1=3 434,法向刚度K2=108 kN/m3(受压),法向刚度K2=7 kN/m3(受拉),n=0.64, Rf=0.88。
|
图 3 如美心墙堆石坝有限元模型 Fig.3 FEM meshes of the Rumei rockfill dam |
| 表 1 如美筑坝料邓肯E-B模型参数 Tab.1 Parameters of the E-B model of the Rumei dam materials |
| 表 2 筑坝料流变模型参数 Tab.2 Parameters of the creep model of the Rumei dam materials |
表 3给出了各时期坝体应力变形极值,图 4~6分别给出了竣工期、蓄水期、运行期8年后坝体位移分布。竣工期、蓄水期、运行期坝体最大沉降分别为284.3,307.9和317.3 cm,沉降率分别达到了0.9%,0.98%和1.0%。竣工期坝体沉降最大值出现在砾石心墙坝轴线处2 686 m高程附近,蓄水后受坝壳湿化、流变效应影响,坝体沉降最大值位置逐渐向上游和向上移动。
| 表 3 大坝应力变形特征值 Tab.3 Extreme values of the dam stress and deformation |

|
图 4 竣工期坝体位移分布(单位:cm) Fig.4 Deformation of the Rumei rockfill dam at completion (unit: cm) |

|
图 5 蓄水初期坝体位移分布(单位:cm) Fig.5 Deformation of the Rumei rockfill dam at the first time of water storage (unit:cm) |

|
图 6 运行8年后坝体位移分布(单位:cm) Fig.6 Deformation of the Rumei rockfill dam after 8 years operation (unit:cm) |
图 7为竣工期和蓄水期坝体孔隙压力分布,可以看出竣工期砾石心墙土内累积了较高的超静孔隙压力,最大值达576.8 kPa,蓄水期心墙内孔压分布规律良好。

|
图 7 坝内孔隙压力分布(单位:kPa) Fig.7 Pore pressure in the dam body (unit: kPa) |
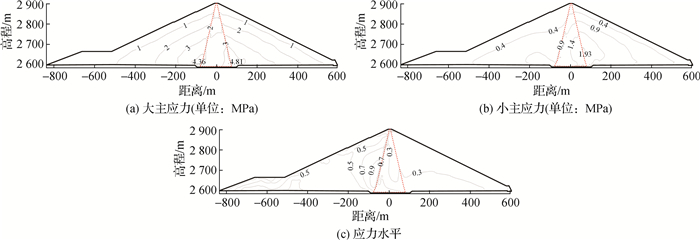
图 8为运行期坝体主应力和应力水平分布,从大主应力分布可以看出,心墙大主应力明显低于坝壳,存在强烈的“拱效应”,大主应力极值出现在坝壳料基底。受水荷载影响,心墙上游坝壳料附近应力水平较高,有发生剪切破坏可能,但由于该区域坝体变形指向坝内一般不会影响大坝整体安全。
|
图 8 运行期坝内主应力和应力水平分布 Fig.8 Stress of the dam during the operation period |
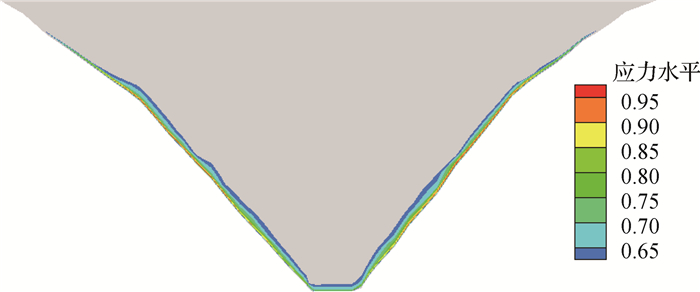
为了防止砾石土心墙与混凝土垫层之间摩擦接触引起心墙剪切破坏,在砾石土心墙底部和混凝土垫层之间设置了高塑性接触黏土层(见图 9)。接触黏土层具有低强度、低模量、高塑性的特点(见表 1),工程上允许接触黏土本身发生剪切破坏,由于其塑性指数高,在较大的含水率区间内均能保证较强的可塑性,可保证心墙基底防渗性以及保护砾质土心墙不发生剪切破坏。如美大坝在河床段设置的接触黏土层厚度为2 m,岸坡段厚度为1 m。图 10为大坝运行期心墙与接触黏土区纵剖面应力水平分布,可以看出,应力水平较高区域位于岸坡陡峭区域,高程2 630~2 810 m范围内接触黏土应力水平基本在0.9以上,达到剪切破坏状态。砾石土心墙区未发生剪切破坏。

|
图 9 砾质心墙和接触黏土示意 Fig.9 Core wall and contact clay |
|
图 10 运行期砾质心墙与接触黏土应力水平 Fig.10 Stress level of the core and the contact clay in the operation period |
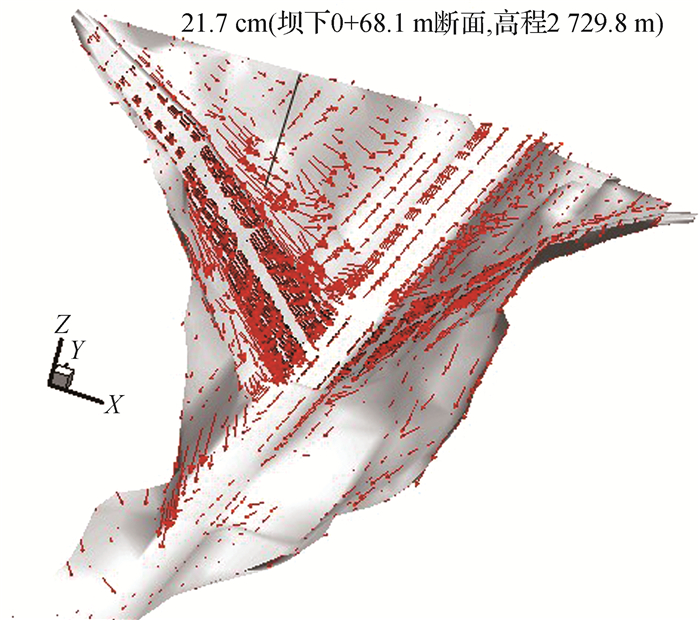
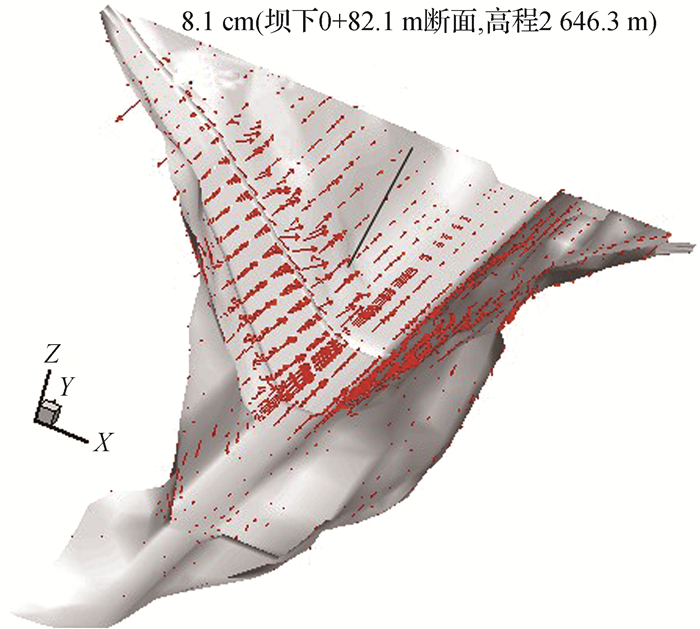
图 11为运行8年后坝体与地基发生的相对摩擦滑动矢量(接触面上下盘相对滑移量),可以看出,坝体与基岩发生了明显的相对滑移,且在地形陡峭部位更为明显,运行期坝体相对基岩最大滑移量达21.7 cm,出现在坝下0+68.1 m断面,2 729.8 m高程。图 12为坝体竣工后在蓄水、湿化、流变作用下产生的坝体相对地基的位移矢量增量,可以看出,工后坝体-地基相对滑移主要表现为坝体相对基岩向下游的滑移变形,受水荷载作用,滑移较大区域出现在心墙迎水面下游区域,最大达8.1 cm(坝下0+82.1 m断面,高程2 646.3 m)。
|
图 11 运行期坝体-地基接触面相对滑移 Fig.11 Displacement between dam-foundation interface during operation period |
|
图 12 工后坝体-地基接触面相对滑移增量 Fig.12 Displacement between dam-foundation interface after dam completion |
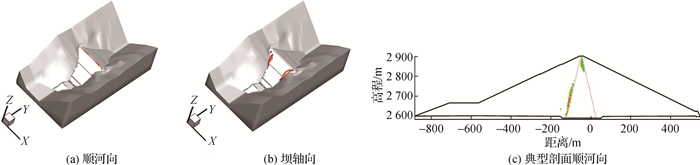
国内外已建的高心墙堆石坝监测资料表明,蓄水、运行期坝顶裂缝较为常见,如瀑布沟心墙堆石坝初次蓄水出现了坝顶纵向裂缝[13]、小浪底斜心墙坝运行期也出现了坝顶纵向裂缝[14]。心墙堆石坝产生坝体裂缝的本质机理是由于坝体变形不协调所致,尤其是湿化、流变效应引起的后期变形。倾度法[15]是判断坝体裂缝的常用方法,沿顺河向倾度定义为γy=∂S/∂y·100%;沿坝轴向倾度定义为γx=∂S/∂x·100%,坝体产生裂缝的临界倾度值尚没有定论,根据一些工程经验,开裂临界值大体取1%[16]。如美大坝倾度γ≥1%的区域分布见图 13。
|
图 13 倾度γ≥1%的区域分布 Fig.13 Zones of γ≥1% of the dam |
图 13(a)为运行期如美大坝顺河向倾度γy≥1%区域分布,可以看出,倾度较大区域位于坝顶,这表明在运行期坝顶可能出现纵向裂缝。图 13(b)为运行期如美大坝轴向倾度γx≥1%区域分布,可以看出,倾度较大区域位于上游坝壳2 850 m高程处,这表明该区域在运行期坝顶出现横向裂缝可能性较高。
图 13(c)为顺河向倾度γy在典型剖面的分布, 可以看出,倾度较大区域出现在坝顶以及上游过渡、反滤料区。坝顶裂缝开展区延伸至心墙下游区对防渗体具有明显的危害,上游过渡、反滤区产生的隐形裂缝出现自愈的可能性高,这是由于该区域坝体变形后期变形指向坝内,一般不会危及坝体安全。由于坝体裂缝主要是由于坝体后期流变、湿化效应导致的,设计与施工过程中可考虑对坝体结构、填筑过程以及蓄水过程进行优化,以控制坝体裂缝的产生和扩展。
5 结语本文对考虑了坝体-地基摩擦接触效应的如美特高心墙堆石坝的结构安全性进行了分析,得到的主要结论如下:
(1) 由于大坝位于狭窄陡峻河谷,坝体与地基出现了明显的相对滑移变形,填筑期以及运行期累积的相对滑移变形达21.7 cm,坝体蓄水运行后产生的相对滑移增量最大值达8.1 cm,受水荷载作用影响,滑移变形最大值出现在坝体下游。可见,对于狭窄河谷上的高土石坝,坝体与地基的相对滑移位移量值较大,计算分析中应予以考虑。
(2) 坝内应力水平总体较低,但受蓄水影响,心墙上游附近堆石区剪应力水平较高,考虑到该区域坝体位移指向坝内,不会影响大坝安全。心墙料与混凝土垫层之间的接触黏土层2 630~2 810 m高程区域应力水平在0.9以上,已达剪切破坏状态,但心墙本身未发生剪切破坏。
(3) 采用倾度有限元法评估了坝体可能出现裂缝的区域,结果表明,运行期坝顶可能产生纵向裂缝,而大坝上游坝坡靠近两岸区域可能产生横向裂缝,坝顶延伸至心墙区域的裂缝会危害坝体安全,对坝体填筑、蓄水过程、结构布置进行优化以控制裂缝的产生和开展。
| [1] |
顾淦臣, 束一鸣, 沈长松. 土石坝工程经验与创新[M]. 北京: 中国电力出版社, 2004. ( GU Ganchen, SHU Yiming, SHEN Changsong. Experience and innovation of earth and rock dam engineering[M]. Beijing: China Electric Power Press, 2004. (in Chinese))
|
| [2] |
KULHAWY F H, DUNCAN J M. Stresses and movements in Oroville dam[J]. Journal of the Soil Mechanics and Foundations Division, 1972, 98(7): 653-665. |
| [3] |
WU Y K, ZHANG B Y, YU Y Z, et al. Consolidation analysis of Nuozhadu high earth-rockfill dam based on the coupling of seepage and stress-deformation physical state[J]. International Journal of Geomechanics, 2015, 16(3): 1-11. |
| [4] |
SKERMER N A. Mica dam embankment stress analysis[J]. Journal of the Geotechnical Engineering Division, 1975, 101: 229-242. |
| [5] |
张启岳, 熊国文. 鲁布革坝的原型观测(一)[J]. 水利水运科学研究, 1994(3): 211-230. ( ZHANG Qiyue, XIONG Guowen. Prototype observation of Lubuge dam Ⅰ[J]. Journal of Nanjing flydraulic Research Institute, 1994(3): 211-230. (in Chinese)) |
| [6] |
宋文晶, 高莲士. 窄陡河谷面板堆石坝坝肩摩擦接触问题研究[J]. 水利学报, 2008, 27(7): 94-100. ( SONG Wenjing, GAO Lianshi. Influence of valley topography on the safety of CFRD anti-seepage systems[J]. Journal of Hydroelectric Engineering, 2008, 27(4): 94-100. (in Chinese)) |
| [7] |
魏匡民, 陈生水, 李国英, 等. 陡峻河谷高面板坝坝体与坝基接触效应[J]. 岩土力学, 2018, 39(9): 3415-3424. ( WEI Kuangmin, CHEN Shengshui, LI Guoying, et al. Influence of contact effect between dam body and dam foundation on behaviors of high CFRDs built in steep valleys[J]. Rock and Soil Mechanics, 2018, 39(9): 3415-3424. (in Chinese)) |
| [8] |
李文轩, 卞士海, 李国英, 等. 粗粒料接触面模型及其在土石坝工程中的应用[J]. 岩土力学, 2019, 40(6): 2379-2388. ( LI Wenxuan, BIAN Shihai, LI Guoying, et al. Interface model of coarse-grained soils and its application in earth rock dam[J]. Rock and Soil Mechanics, 2019, 40(6): 2379-2388. (in Chinese)) |
| [9] |
MAURICE A B. General theory of three-dimensional consolidation[J]. Journal of Applied Physics, 1941, 12(2): 155-164. DOI:10.1063/1.1712886 |
| [10] |
李国英, 米占宽, 傅华, 等. 混凝土面板堆石坝堆石料流变特性试验研究[J]. 岩土力学, 2004, 25(11): 1712-1716. ( LI Guoying, MI Zhankuan, FU Hua, et al. Experimental studies on rheological behaviors for rockfills in concrete faced rockfill dam[J]. Rock and Soil Mechanics, 2004, 25(11): 1712-1716. DOI:10.3969/j.issn.1000-7598.2004.11.007 (in Chinese)) |
| [11] |
殷宗泽. 土工原理[M]. 北京: 中国水利水电出版社, 2007. ( YIN Zongze. Principles of geotechnical engineering[M]. Beijing: China Water Resources and Hydropower Press, 2007. (in Chinese))
|
| [12] |
CLOUGH G W, DUNCAN J M. Finite element analyses of retaining wall behavior[J]. Journal of the Soil Mechanics and Foundations Division, 1971, 97(SM12): 1657-1672. |
| [13] |
林道通, 朱晟, 邬铭科, 等. 瀑布沟砾石土心墙堆石坝初次蓄水期坝顶裂缝成因分析[J]. 水力发电, 2017, 43(10): 56-61. ( LIN Daotong, ZHU Sheng, WU Mingke, et al. Cause analysis of crest cracking of Pubugou rockfill dam with a central gravelly soil core during first reservoir impounding[J]. Water Power, 2017, 43(10): 56-61. (in Chinese)) |
| [14] |
韩朝军, 朱晟. 土质防渗土石坝坝顶裂缝开裂机理与成因分析[J]. 中国农村水利水电, 2013(8): 116-120. ( HAN Chaojun, ZHU Sheng. Cracking mechanism and cause analysis in earth-rock dam[J]. China Rural Water and Hydropower, 2013(8): 116-120. DOI:10.3969/j.issn.1007-2284.2013.08.030 (in Chinese)) |
| [15] |
李君纯. 土坝裂缝的简捷估算方法[J]. 水利水运科学研究, 1983(3): 1-11. ( LI Junchun. Simple calculation method of soil dam crack[J]. Journal of Nanjing Hydraulic Research Institute, 1983(3): 1-11. (in Chinese)) |
| [16] |
张丙印, 张美聪, 孙逊. 土石坝横向裂缝的土工离心机模型试验研究[J]. 岩土力学, 2008, 29(5): 1254-1258. ( ZHANG Bingyin, ZHANG Meicong, SUN Xun. Centrifugal modeling of transverse cracking in earth core dams[J]. Rock and Soil Mechanics, 2008, 29(5): 1254-1258. DOI:10.3969/j.issn.1000-7598.2008.05.020 (in Chinese)) |
2. PowerChina Guiyang Engineering Corporation Limited, Guizhou 550081, China
 2019
2019 