2. 浙江省河口海岸重点实验室,浙江 杭州 310020
据不完全统计,世界上大约有450个河口存在涌潮[1]。目前,我国钱塘江、长江口北支[2]、浙江椒江干流灵江和浙江鳌江河口[3]均存在涌潮,其中钱塘江涌潮强度大,潮景多变,且两岸交通方便,是世界上最有欣赏价值的涌潮[4]。另一方面,钱塘江涌潮对涉水工程的破坏力极大,是引起钱塘江两岸毁堤成灾、涉水建筑物破坏的主要原因之一。特别在台风期间,台风一方面引起外海高潮位抬高、潮差增大[5],进而导致涌潮强度增大[6];另一方面,台风期间较大的局地顺风导致涌潮传播速度加快,涌潮流速猛增[7]。上述两个因素相互作用,年最大涌潮几乎都发生在台风期间,此时涌潮最为壮观,同时带来的破坏力也最大。因此,为保护钱塘江涌潮这一宝贵的自然资源,同时缓解乃至消除其灾害,开展台风对钱塘江涌潮影响研究,具有十分重要的学术意义和实际应用价值。
最近10余年来,大尺度涌潮数值模型取得了突破性的进展。潘存鸿等先后采用Godunov格式[8]和KFVS(Kinetic Flux Vector Splitting)格式[6]建立了基于三角形网格的“和谐”二维涌潮数值模型,模拟了涌潮形成、发展和衰减的全过程;张舒羽等[7]基于上述KFVS格式的涌潮数学模型探讨了概化河道中风况对涌潮的影响;Lu等[9]应用WENO格式模拟了钱塘江二维涌潮;李绍武等[10]建立了准三维涌潮数学模型;谢东风等[11]应用FVCOM模型进行了钱塘江涌潮的三维数值模拟;程文龙等[12]研究了FVCOM模型关键参数并进行了处理,改善了涌潮计算结果;汪求顺等[13]应用FVCOM模型数值研究了不同湍流模式对涌潮计算结果的影响。
在天文潮和风暴潮非线性耦合的台风暴潮数值研究方面,国内外都取得了较大进展。谢亚力等[14]和Guo等[15]应用数值模型分别研究了钱塘江河口治江缩窄对杭州湾台风暴潮的影响。黄世昌等[16]和郑立松等[17]分别应用台风暴潮数值模型计算分析了杭州湾风暴增水与天文潮的非线性效应;于普兵等[5]建立了杭州湾台风暴潮实时预报模型,并得到了很好的应用。
综上所述,涌潮和风暴潮数值模拟研究已取得了许多成果,但台风暴潮对涌潮作用研究还罕见公开报道。考虑到台风过程中风场的非恒定性和复杂性,为简化研究,本文基于FVCOM模型研究了顺风和逆风条件下恒定风况对涌潮的作用,分析了风况对涌潮特征的影响。
1 台风期间实测潮汐资料初步分析东海潮波传入杭州湾后,因受杭州湾两岸岸线向上游缩窄及乍浦以上床底抬升的影响,潮波能量积聚,浅水变形加剧,最终在澉浦上游形成涌潮。涌潮形成后向上游逐渐增大,在大缺口至盐官河段达到最大,涌潮高度一般为1~2 m,最大可达3 m以上,盐官以上涌潮逐渐减弱,涌潮最远可达闻堰以上,从起潮点算起,涌潮河段长达120 km左右。涌潮过后的涌潮流速测点实测最大为6.54 m/s,涌潮传播速度一般为3~7 m/s[6, 18]。
鉴于台风期间涌潮观测的困难及其危险性,台风期间钱塘江涌潮实测资料非常缺乏,现对收集到的风况、潮汐等相关资料作初步分析。
1.1 台风对潮汐特征的影响1997年以后对钱塘江河口影响较大的几次台风资料见表 1,表中潮差与涨潮历时的差值为实测值与天文潮的差值,潮波传播速度为台风期实测值与台风前实测值的差值。由表 1可知:①台风期间,杭州湾海盐风向一般为ENE方向,有利于潮波上溯,导致杭州湾潮差增大,各台风澉浦潮差增大0.26~1.11 m,相对增大4.2%~22.8%。②台风期间,除0509和1509台风外,一般情况下高、低潮位出现时间均提前,且高潮位出现时间更早,因此涨潮历时缩短,各台风期间澉浦涨潮历时缩短11~39 min,相对缩短3.3%~13.4%。③台风期间,在东北风向作用下,潮波(涌潮)传播速度加快,台风期间从澉浦到盐官加快0.06~0.77 m/s,相对加快1.9%~26.7%。
| 表 1 台风期潮汐特征 Tab.1 Tidal characteristics during typhoons |
涌潮特征与潮汐特征密切相关[6]。台风造成起潮点下游澉浦潮差增大,涨潮历时缩短,潮波传播速度加快,从而导致涌潮高度增大,涌潮流速加大,涌潮传播速度加快。
对于固定位置,在其他条件相同情况下,涌潮高度与当地潮差密切相关,潮差越大,涌潮越强。根据2010年10月盐官涌潮实测资料,盐官涌潮高度ΔH与潮差A的相关关系为(相关系数为0.98)[19]:ΔH=0.95A-2.24。
盐官潮差与澉浦潮差、涌潮流速与当地潮差均存在良好的正相关关系,从而得到澉浦潮差越大,盐官潮差越大,涌潮也越大。即台风促使盐官河段涌潮增大,涌潮流速也加大。
2 三维数值模型简介及其验证计算 2.1 三维数值模型简介FVCOM模型的控制方程为雷诺时均的三维σ坐标下N-S方程[20],其中垂向采用静压假定。
| $ \frac{\partial \zeta}{\partial t}+\frac{\partial(D u)}{\partial x}+\frac{\partial(D v)}{\partial y}+\frac{\partial w}{\partial \sigma}=0 $ | (1) |
| $ \begin{array}{c} \frac{\partial(u D)}{\partial t}+\frac{\partial\left(u^{2} D\right)}{\partial x}+\frac{\partial(u v D)}{\partial y}+\frac{\partial(u w)}{\partial \sigma}=f v D-g D \frac{\partial \zeta}{\partial x}+\frac{\tau_{\mathrm{s}x}-\tau_{\mathrm{b}x}}{\rho_{0}}+\\ \frac{1}{D} \frac{\partial}{\partial \sigma}\left(K_{\mathrm{m}} \frac{\partial u}{\partial \sigma}\right)+\frac{\partial}{\partial x}\left[2 A_{\mathrm{m}} H \frac{\partial u}{\partial x}\right]+\frac{\partial}{\partial y}\left[A_{\mathrm{m}} H\left(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\right)\right] \end{array} $ | (2) |
| $ \begin{array}{c} \frac{\partial(v D)}{\partial t} +\frac{\partial\left(v^{2} D\right)}{\partial y}+\frac{\partial(u v D)}{\partial x}+\frac{\partial(v w)}{\partial \sigma}=-f u D-g D \frac{\partial \zeta}{\partial y}+\frac{\tau_{\mathrm{sy}}-\tau_{\mathrm{by}}}{\rho_{0}}+\\ \frac{1}{D} \frac{\partial}{\partial \sigma}\left(K_{\mathrm{m}} \frac{\partial v}{\partial \sigma}\right)+\frac{\partial}{\partial y}\left[2 A_{\mathrm{m}} H \frac{\partial v}{\partial y}\right]+\frac{\partial}{\partial x}\left[A_{\mathrm{m}} H\left(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\right)\right] \end{array} $ | (3) |
式中:t为时间;x,y和σ分别为水平和垂向坐标;ζ为水面的高度;u,v,w分别为x, y, σ方向流速;D为全水深;H为静水深;f为科氏常数;g为重力加速度;ρ0为水密度;Am为水平紊动黏性系数;Km为垂向涡黏系数。湍流方程采用修正Mellor-Yamada 2.5阶紊流模型计算。τsx,τsy分别为x,y方向风应力,τsx=cdρa(u10+ v10)0.5 u10,τsy=cdρa(u10+ v10)0.5 v10。其中:Cd为风的拖曳系数,选用Large和Pond建立的公式进行计算[21];ρa为空气密度;u10,v10分别为x,y方向水面以上10 m的风速。τbx,τby分别为x,y方向底部切应力,τbx=cbρ0 (ub+vb)0.5ub,τby=cbρ0(ub+vb)0.5vb,其中:Cb为底部摩阻系数,根据以往研究成果,采用较小糙率系数的曼宁公式进行计算;ub,vb分别为x,y方向床面的流速。
对模型中的关键参数糙率系数和垂向紊动系数的选取作了改进[12],计算离散方法详见文献[20]。
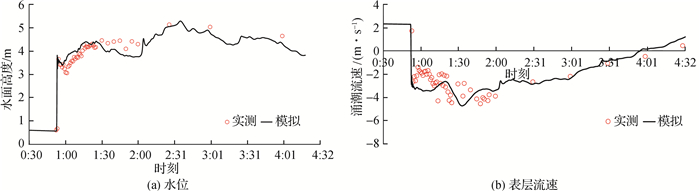
2.2 模型验证模型计算范围从下游的澉浦到上游的杭州闸口(图 1),计算域采用无结构三角形网格离散,平面上共布置41 221个单元,相邻节点间的最小距离为30 m,垂向上分成12层。模型验证采用2010年10月实测潮汐和涌潮资料,江道地形根据2010年7月实测1:50 000地形数据进行概化,上、下水边界均采用实测潮位,澉浦潮差7.81 m。外模和内模的时间步长分别为0.05和0.50 s。模型验证了7个潮位站的潮位过程、6个站(丁桥北和南、盐官北和南、胡头北和南)的涌潮过程以及5个测点的流速和流向过程。经验证,当曼宁糙率系数取0.006 5~0.015 0 m-1/3·s范围时验证结果较好。限于篇幅,图 2仅给出了盐官站涌潮到达前后水位和表层流速的验证。由图 2可知,涌潮过后约1 h内,潮位、流速变化幅度很大,尽管潮位总体上涨,但过程并不单调,同样流速跳动也很大,比无涌潮水流复杂得多。因此,要准确验证潮位、流速变化过程的细节非常困难。但从涌潮前后水位和流速的变化可知,建立的数学模型反映了涌潮水流的水位猛增和流速的突变过程。

|
图 1 模型计算范围 Fig.1 Sketch of study area and computational domain |
|
图 2 盐官站涌潮到达前后水位和表层流速验证 Fig.2 Validation of water level and velocity at the surface layer during the tidal bore passage at Yanguan |
为研究风况对涌潮的影响,以无风作为基础方案,设置了顺风(东风)和逆风(西风)两个方向,10,20,30 m/s共3个风速的6个计算方案,增加下边界涨潮开始加风的东风30*方案,其余方案始终加风。以盐官河段作为主要研究河段,计算中采用的江道地形、水边界条件均同验证计算一致。其中,风拖曳系数Cd按下式[21]计算:
| $ C_{\mathrm{d}}=\left\{\begin{array}{lc} {1.20 \times 10^{-3}, } & {u<11 \mathrm{m} / \mathrm{s}} \\ {(0.49+0.065 u) \times 1.0 \times 10^{-3}, } & {11 \mathrm{m} / \mathrm{s} \leqslant u \leqslant 25 \mathrm{m} / \mathrm{s}} \\ {(0.49+0.065 \times 25) \times 1.0 \times 10^{-3}, } & {u>25 \mathrm{m} / \mathrm{s}} \end{array}\right. $ | (4) |
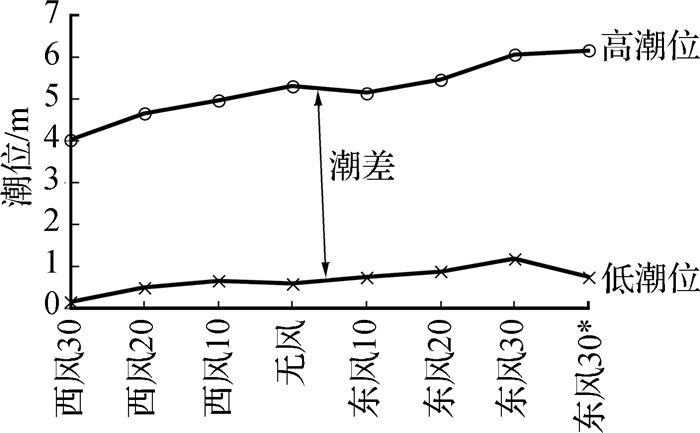
潮汐特征特别是潮差直接影响涌潮大小。对于某一固定位置,一般潮差越大,涌潮越强[6]。图 3为不同风况情况下盐官潮汐特征。由图 3可知,顺风一般导致高潮位抬高,逆风引起高潮位降低,并且风速越大,影响越大。同样,顺风导致低潮位抬高,逆风一般引起低潮位降低,并且风速越大,影响越大;东风30*方案因仅在涨潮时加风,故该方案对盐官低潮位影响不大。顺风对潮差的影响比较复杂,东风10和东风20方案潮差有所减小,而东风30方案潮差有所增大,东风30*方案潮差增大幅度最大;逆风引起潮差减小。顺风导致潮差增大的计算结果与实测资料在定性上一致。
|
图 3 不同风况盐官潮汐特征 Fig.3 Characteristics of tides under different winds at Yanguan |
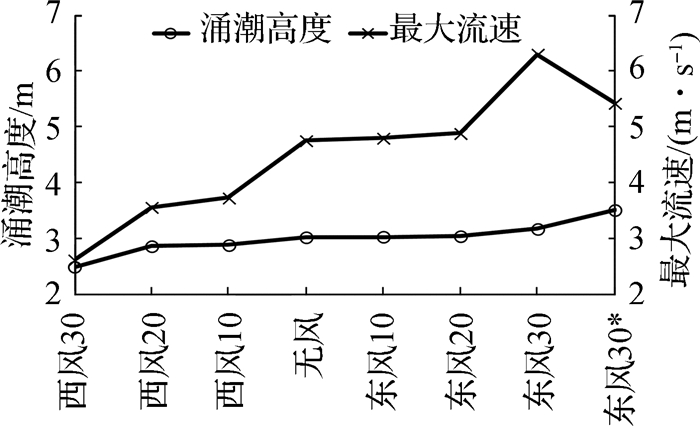
图 4绘出了不同风况下盐官涌潮高度,图 5为顺风和逆风情况下盐官涌潮过程。由图 4可知,顺风促使涌潮增大,逆风引起涌潮减小,且风速越大,增减幅度越大;同样风速下,逆风引起涌潮减小的幅度大于顺风促使涌潮增大的幅度;除西风30和东风30*方案外,其他方案对涌潮高度的影响不是很大,增减值大致在5%以内。
|
图 4 不同风况盐官涌潮高度和最大流速 Fig.4 Tidal bore height and the maximum velocity under different winds at Yanguan |

|
图 5 顺风和逆风情况下盐官涌潮过程 Fig.5 Water level of tidal bores under favorable wind and head wind at Yanguan |
东风30*方案,由于仅在下边界澉浦涨潮时开始加风,对盐官的低潮位抬高影响较小,故潮差增大最多,相应地涌潮高度也增大最多。
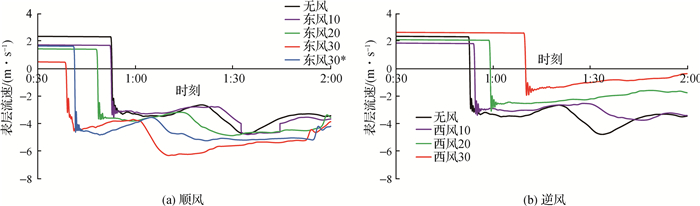
3.3 风对涌潮流速的影响不同风况下盐官表层涌潮流速过程如图 6。由图 6可知,顺风促使涌潮流速增大,逆风引起涌潮流速减小,且风速越大,增减幅度越大;在同样风速下,逆风引起涌潮流速减小的幅度大于顺风促使涌潮流速增大的幅度;在同样风速下,涌潮最大流速的变化幅度比涌潮高度变化幅度大得多,如东风30方案,涌潮高度仅增加5%,而涌潮最大流速增大33%,西风30方案,涌潮高度减小18%,而涌潮最大流速减小45%。
|
图 6 顺风和逆风情况下盐官表层流速过程 Fig.6 Velocity at the surface layer under favorable wind and head wind at Yanguan |
不同风况对涌潮流速过程的影响也不同。无风和顺风条件下流速有2个峰值,而逆风条件下只有西风10方案有2个流速峰值,西风20和西风30方案只有1个流速峰值。
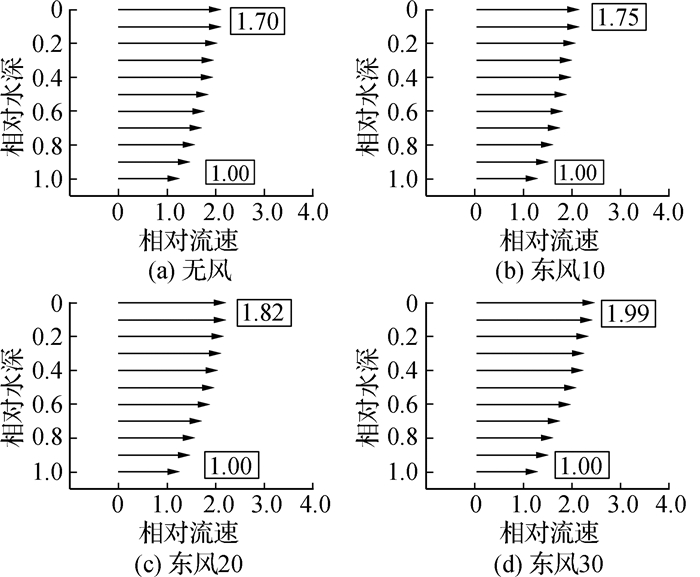
风况对涌潮流速垂向分布影响较大,图 7和8为顺风和逆风情况下涌潮流速最大时刻涌潮流速垂向分布。图中横坐标为相对流速,设底层流速为1。无风条件下涌潮最大流速出现在表层,从表层到底层涌潮流速逐渐减小,表层流速与底层之比为1.70。
|
图 7 顺风情况下盐官涌潮流速垂向分布 Fig.7 Vertical distribution of tidal bore velocity under favorable wind at Yanguan |

|
图 8 逆风情况下盐官涌潮流速垂向分布 Fig.8 Vertical distribution of tidal bore velocity under head wind at Yanguan |
顺风时,表层最大流速增大,风速越大,增加幅度越大,如东风10、东风20和东风30方案,与无风方案相比,表层最大流速分别增加了2%, 7%和14%。而中、下层流速相对变化较小。因此,在涌潮流速最大时刻涌潮流速垂向分布更加不均匀,上述3个顺风方案表层流速与底层流速之比分别为1.75, 1.82和1.99,如图 7。
逆风时,表层最大流速减小,风速越大,减小幅度越大,如西风10、西风20和西风30方案,与无风方案相比,在涌潮流速最大时刻表层流速分别减小5%, 44%和54%。在涌潮流速垂向分布上,西风10方案最大流速仍在表层,表层流速与底层之比为1.62;西风20和西风30方案最大流速均位于中下层,且底层流速大于表层流速,表层流速与底层之比分别为0.96和0.78,如图 8。
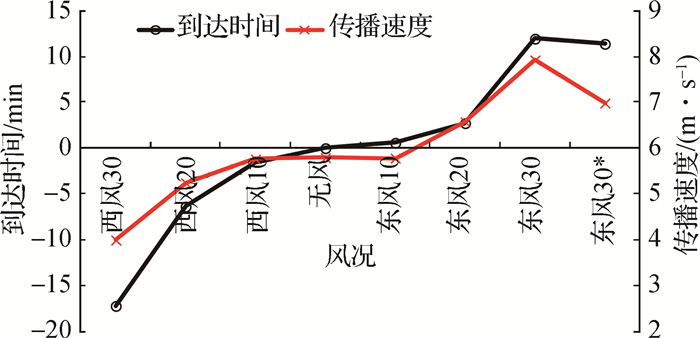
3.4 风对涌潮传播速度的影响为比较不同风况下涌潮传播速度,设无风下涌潮到达盐官的时间为0,图 9为不同风况下盐官涌潮到达时间的比较,其中“+”表示涌潮达到时间提前,“-”表示涌潮到达时间滞后。可见,顺风促使涌潮传播速度加快,逆风导致涌潮传播速度减慢,且风速越大,增减幅度越大。同样风速下,逆风引起涌潮传播速度减慢的幅度大于顺风促使涌潮传播速度加快的幅度,如东风30方案盐官涌潮到达时间比无风时早11 min 57 s,而西风30方案盐官涌潮到达时间比无风时迟17 min 13 s。上述结果与基于涌潮传播速度计算公式[6]得到的结果在定性上是一致的。
|
图 9 不同风况下盐官涌潮到达时间及传播速度 Fig.9 Arrival time and propagation speed under different winds at Yanguan |
盐官至胡斗的涌潮传播速度同绘于图 9,西风30方案涌潮传播速度最慢,为4.0 m/s,比无风条件下慢31%;东风30方案涌潮传播速度最快,为7.9 m/s,约为前者的2倍,比无风条件下快37%。其他方案的涌潮传播速度介于上述之间。计算结果与实测值在定性上一致。
3.5 风对涌潮潮景的影响钱塘江涌潮在传播过程中,因受岸线形状、江道地形以及涉水工程等影响形成涌潮潮景,其中最为著名的是大缺口以下的交叉潮、盐官的一线潮和老盐仓的回头潮[6]。交叉潮一般只有在江道存在中沙的条件下才能形成,由于涌潮尺度小,要准确模拟二股涌潮相交,要求网格尺度很小,为此,本文仅模拟了一线潮和回头潮。
盐官河段岸线顺直,河宽几乎相同,河床断面近似成“U”形,因此,往往发育“一”字型的一线潮。根据前文分析,尽管风况对盐官河段的涌潮高度有一定影响,但影响幅度并不大。影响杭州湾的台风在登陆前大多为偏东风,对盐官河段而言为顺风,涌潮高度略有增大,但肉眼一般难以观测到其变化。因此,模型计算成果与实际情况基本符合。
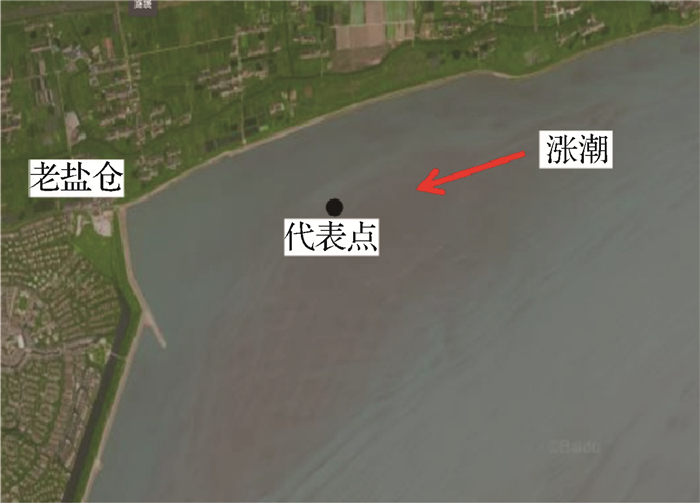
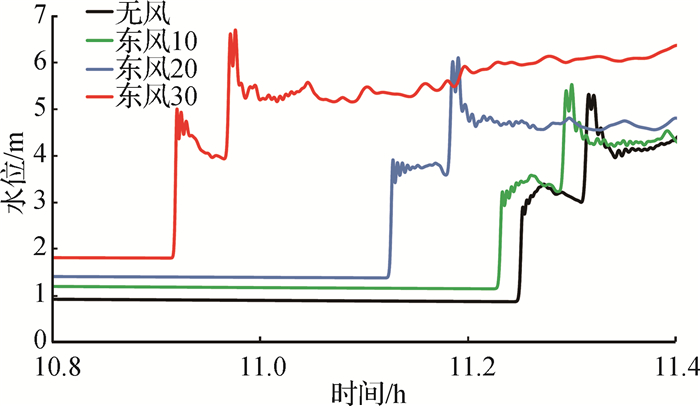
涌潮传播到老盐仓河段,受老盐仓直角岸线和丁坝的影响(见图 10),涌潮几近正反射,图 11为代表点在无风、东风10、东风20和东风30等方案的涌潮及回头潮过程。图 11中潮位过程第1个台阶为涌潮,第2个台阶为回头潮。由图 11可知,无风情况下涌潮高度为2.14 m,回头潮高度为2.32 m。与无风方案相比,顺风方案存在以下特点:①潮前低水位抬高,东风10、东风20和东风30方案比无风情况下分别抬高0.28,0.52和0.94 m。②涌潮高度有所增大,东风10、东风20和东风30方案比无风情况下分别增大1%,8%和26%。③回头潮高度有所增大,东风10、东风20和东风30方案比无风情况下分别增大 < 1%,5%和16%。④一方面低潮位抬高,另一方面涌潮高度和回头潮高度均增大,因此回头潮水位明显抬高,东风10、东风20和东风30方案比无风情况下分别抬升0.22,0.71和1.32 m。⑤涌潮传播速度加快,涌潮及回头潮到达时间提前,在计算下边界澉浦潮到时间相同的条件下,东风10、东风20和东风30方案比无风情况下涌潮到达时间分别提前72,450和1 195 s,回头潮到达时间分别提前76,464和1 234 s。由于涌潮能量增大,涌潮反射后潮动能转化为潮势能的能量也相应增大,这从另一角度解释了回头潮水位抬高的原因。实际情况是台风期间,老盐仓回头潮的水位明显抬高,经常出现回头潮翻越海堤堤顶、破坏防浪墙的情况,上述计算结果反映了这一现象。
|
图 10 老盐仓河段及代表点位置 Fig.10 Location of the representative point at the Laoyancang Reach |
|
图 11 代表点涌潮及回头潮过程 Fig.11 Water level of tidal bore and back-flow bore at the representative point |
本文基于三维涌潮数值模型计算分析了顺风和逆风条件下不同风速对钱塘江涌潮的影响,结合实测资料分析,得出的主要结论如下:
(1) 台风期间,在大范围风场和气压场作用下,一般起潮点下游澉浦潮差增大,涨潮历时缩短,潮波传播速度加快,从而导致涌潮高度增大,涌潮流速加大,涌潮传播速度加快。
(2) 顺风作用使得涌潮高度、流速和传播速度均增大,风速愈大,增幅愈大。在顺风30 m/s风况下,盐官涌潮高度增加5%,涌潮流速增大33%,涌潮传播速度加快37%;顺风风速愈大,表层涌潮流速增加愈大,涌潮流速沿水深分布愈不均匀,在顺风10,20,30 m/s风况下,表、底层流速之比分别为1.75,1.82和1.99。
(3) 在逆风作用下,涌潮高度、流速和传播速度均减小,风速愈大,减小幅度愈大。在逆风30 m/s风况下,盐官涌潮高度减小18%,涌潮流速减小45%,涌潮传播速度减小31%;逆风风速愈大,表层涌潮流速减小愈明显。在逆风20和30 m/s风况下,最大流速均位于中下层,且底层流速大于表层流速,表层流速与底层之比分别为0.96和0.78。
(4) 顺风作用导致老盐仓回头潮更强。在顺风10,20和30 m/s风况下,比无风情况下回头潮分别增大 < 1%,5%和16%。因潮前低潮位抬高,涌潮高度和回头潮高度均增大,因此回头潮水位明显抬高,顺风10,20和30 m/s风况比无风情况下分别抬升0.22,0.71和1.32 m。这与台风期间老盐仓经常出现回头潮翻越海堤堤顶的情况相一致。
| [1] |
CHANSON H. Current knowledge in tidal bores and their environmental, ecological and cultural impacts[J]. Environmental Fluid Mechanics, 2011, 11(1): 77-98. |
| [2] |
许宝华, 乔红杰. 长江口北支涌潮现状分析[J]. 长江科学院院报, 2019, 36(5): 13-17. ( XU Baohua, QIAO Hongjie. Current situation of tidal bore in North Branch of the Yangtze River Estuary[J]. Journal of Yangtze River Scientific Research Institute, 2019, 36(5): 13-17. (in Chinese)) |
| [3] |
《鳌江志》编纂委员会. 鳌江志[M]. 北京: 中华书局, 1999. ( Compilation Committee of Aojiang River Records. Aojiang river zhi[M]. Beijing: Zhonghua Book Company, 1999. (in Chinese))
|
| [4] |
潘存鸿, 韩曾萃. 钱塘江河口保护与治理研究[M]. 北京: 中国水利水电出版社, 2017. ( PAN Cunhong, HAN Zengcui. Research on conservation and regulation of Qiantang Estuary[M]. Beijing: China Waterpower Press, 2017. (in Chinese))
|
| [5] |
于普兵, 潘存鸿, 谢亚力. 二维风暴潮实时预报模型及其在杭州湾的应用[J]. 水动力学研究与进展(A辑), 2011, 26(6): 747-756. ( YU Pubing, PAN Cunhong, XIE Yali. 2-dimensional real time forecasting model for storm tides and its application in Hangzhou Bay[J]. Chinese Journal of Hydrodynamics(SerA), 2011, 26(6): 747-756. (in Chinese)) |
| [6] |
潘存鸿, 鲁海燕, 曾剑. 钱塘江涌潮特性及其数值模拟[J]. 水利水运工程学报, 2008(2): 1-9. ( PAN Cunhong, LU Haiyan, ZENG Jian. Characteristic and numerical simulation of tidal bore in Qiantang River[J]. Hydro-Science and Engineering, 2008(2): 1-9. (in Chinese)) |
| [7] |
张舒羽, 潘存鸿. 径流和风对涌潮影响的数值模拟[J]. 海洋工程, 2013, 31(3): 54-62. ( ZHANG Shuyu, PAN Cunhong. Effect of runoff and wind on tidal bore using numerical model[J]. The Ocean Engineering, 2013, 31(3): 54-62. (in Chinese)) |
| [8] |
潘存鸿. 三角形网格下求解二维浅水方程的和谐Godunov格式[J]. 水科学进展, 2007, 18(2): 204-209. ( PAN Cunhong. Well-balanced Godunov-type scheme for 2D shallow water flow with triangle mesh[J]. Advances in Water Science, 2007, 18(2): 204-209. (in Chinese)) |
| [9] |
LU C N, QIU J X, WANG R Y. Weighted essential non-oscillatory schemes for tidal bore on unstructured meshes[J]. International Journal for Numerical Methods in Fluids, 2009, 59(6): 611-630. |
| [10] |
李绍武, 卢丽锋, 时钟. 河口准三维涌潮数学模型研究[J]. 水动力学研究与进展(A辑), 2004, 19(4): 407-415. ( LI Shaowu, LU Lifeng, SHI Zhong. A quasi-3D numerical model for estuarine tidal bore[J]. Journal of Hydrodynamics(SerA), 2004, 19(4): 407-415. (in Chinese)) |
| [11] |
谢东风, 潘存鸿, 吴修广. 基于FVCOM模式钱塘江河口涌潮三维数值模拟研究[J]. 海洋工程, 2011, 29(1): 47-52. ( XIE Dongfeng, PAN Cunhong, WU Xiuguang. Three-dimensional numerical modeling of tidal bore in Qiantang based on FVCOM[J]. The Ocean Engineering, 2011, 29(1): 47-52. (in Chinese)) |
| [12] |
程文龙, 潘存鸿, 吴修广. FVCOM模型关键参数的处理及其在涌潮模拟中的应用[J]. 海洋学研究, 2017, 35(1): 33-40. ( CHENG Wenlong, PAN Cunhong, WU Xiuguang. Processing on key parameter in FVCOM and its application on tidal bore simulation[J]. Journal of Marine Science, 2017, 35(1): 33-40. (in Chinese)) |
| [13] |
汪求顺, 潘存鸿. 不同湍流模式下钱塘江涌潮水流三维模拟[J]. 海洋工程, 2017, 35(1): 80-89. ( WANG Qiushun, PAN Cunhong. Three-dimensional simulation of tidal bore in the Qiantang estuary under different turbulence models[J]. The Ocean Engineering, 2017, 35(1): 80-89. (in Chinese)) |
| [14] |
谢亚力, 黄世昌, 王瑞锋, 等. 钱塘江河口围涂对杭州湾风暴潮影响数值模拟[J]. 海洋工程, 2007, 25(3): 61-67. ( XIE Yali, HUANG Shichang, WANG Ruifeng, et al. Numerical simulation of effects of reclamation in Qiantang Estuary on storm surge at Hangzhou Bay[J]. The Ocean Engineering, 2007, 25(3): 61-67. (in Chinese)) |
| [15] |
GUO Y K, ZHANG J S, ZHANG L X, et al. Computational investigation of typhoon-induced storm surge in Hangzhou Bay, China[J]. Estuarine, Coastal and Shelf Science, 2009, 85(4): 530-536. |
| [16] |
黄世昌, 李玉成, 谢亚力, 等. 杭州湾湾内天文潮与风暴潮耦合模式建立与应用[J]. 大连理工大学学报, 2010, 50(5): 735-741. ( HUANG Shichang, LI Yucheng, XIE Yali, et al. Construction of mode coupling astronomical tide with storm surge and its application in Hangzhou Bay[J]. Journal of Dalian University of Technology, 2010, 50(5): 735-741. (in Chinese)) |
| [17] |
郑立松, 余锡平. 杭州湾内风暴潮与天文潮的耦合效应[J]. 应用基础与工程科学学报, 2013, 21(1): 107-115. ( ZHENG Lisong, YU Xiping. Interaction between storm surge and astronomical tide in Hangzhou Bay[J]. Journal of Basic Science and Engineering, 2013, 21(1): 107-115. (in Chinese)) |
| [18] |
潘存鸿, 潘冬子, 鲁海燕, 等. 钱塘江涌潮流速研究[J]. 海洋工程, 2017, 35(5): 33-41. ( PAN Cunhong, PAN Dongzi, LU Haiyan, et al. Study on velocity of tidal bore in Qiantang Estuary[J]. The Ocean Engineering, 2017, 35(5): 33-41. (in Chinese)) |
| [19] |
谢东风, 潘存鸿, 陆波, 等. 基于实测资料的钱塘江涌潮水动力学特性研究[J]. 水动力学研究与进展(A辑), 2012, 27(5): 501-508. ( XIE Dongfeng, PAN Cunhong, LU Bo, et al. A study on the hydrodynamic characteristics of the Qiantang tidal bore based on field data[J]. Chinese Journal of Hydrodynamics(SerA), 2012, 27(5): 501-508. (in Chinese)) |
| [20] |
CHEN C S, LIU H D, BEARDSLEY R C. An unstructured grid, finite-volume, three-dimensional, primitive equations ocean model: application to coastal ocean and estuaries[J]. Journal of Atmospheric and Oceanic Technology, 2003, 20(1): 159-186. |
| [21] |
LARGE W G, POND S. Open ocean momentum flux measurements in moderate to strong winds[J]. Journal of Physical Oceanography, 1981, 11(3): 324-336. |
2. Zhejiang Provincial Key Laboratory of Estuary and Coast, Hangzhou 310020, China
 2019
2019 