2. 交通运输部天津水运工程科学研究院, 天津 300456
珊瑚礁地形复杂,呈现不同的坡度变化。远海地区的珊瑚礁地形多数为自1 000 m以上深水中凸出的环礁[1],出水的礁坪水深很浅,同时珊瑚礁前常为1: 10~1: 0.5的陡坡,这与缓坡地形明显不同,而这种坡度陡变的珊瑚礁地形对波浪的传播和变形产生了很大的影响。珊瑚岛礁护岸工程是保障后方建筑物安全稳定的第一道屏障,为增大空间利用面积,护岸工程建设往往靠近礁缘,因而显著缩短了礁坪宽度,限制了礁坪上方的波流传播距离与能量耗散空间,进而导致护岸前沿水位的抬升和波流动力的增强,对护岸工程本身的安全产生不利影响。
对于波浪在天然珊瑚礁地形上的传播变形规律,国内外学者开展了大量研究,其中水槽物理模型试验是最常用的研究手段。Gourlay[2-3]对岛礁不同的平均水位和入射波高引起的波浪增水及波生流进行了一系列的规则波试验,发现当平均水位远高于礁坪时,岛礁水动力主要受礁坪底摩阻控制;当平均水位等于或低于礁坪时,岛礁水动力主要受礁缘波浪破碎的控制。在Gourlay的试验中,没有给出模型比尺,但考虑到礁坪上水深一般为0~2 m,根据水深比尺反推其试验的最大原型波高为4.76 m。Yao等[4-5]在实验室中对规则波和不规则波的破碎特征与礁坪水深和礁前坡度的关系进行了研究,其模拟的最大原型波高为2 m。Hench等[6-7]对现场的波浪传播变形规律进行了研究,但观测到的最大波高也仅限于2.6 m的平常波浪条件。对于岛礁工程的安全稳定,50年或100年一遇的重现期波浪是工程设计的控制工况,而上述研究均未涉及极端波浪的传播特征。国内学者赵子丹等[8]结合珊瑚礁地形,综述了台阶式水深剧变地形上的波浪传播研究进展。张庆河等[9]对规则波在台阶地形上的破碎规律进行了试验研究,并给出了描述波浪临界破碎、破碎带宽及波浪衰减规律的经验公式。Shi等[10-11]采用数学模型和物理模型试验研究了礁冠的存在和不同的礁冠宽度对波浪传播变形及礁坪增水的影响,发现礁冠能显著改变波浪在礁坪上的运动特性。任冰等[12]研究了规则波在岛礁地形上传播变化特性。李绍武等[13]对不规则波在岸礁地形增水变化规律进行了小水槽试验研究。由于水槽尺度和模型比尺的限制,极端条件下的波浪在礁坪上的传播特性考虑得比较少。陈松贵等[14-16]采用大水槽试验分别对珊瑚礁地形上的波浪增水、胸墙受力和直立堤越浪量进行了研究,但未详细探讨工程建设对礁坪上波浪传播的影响。
在极端条件下,随着波高的增大,波浪在礁缘处的破碎和紊动更加强烈,传播特征也会与小波高的情况有所不同。同时,岛礁护岸的修建阻断了波浪的传播路径,使得波浪在礁坪上的传播过程更为复杂。针对这些问题,本文将利用大比尺波浪水槽,通过对比分析礁坪上不同位置波高、波谱和增水在护岸工程修建前后的变化,分析珊瑚岛礁护岸对礁坪上极端波浪传播特性的影响,为珊瑚礁工程的设计提供依据。
1 试验设置 1.1 试验设备本试验在大比尺波浪水槽中完成。该水槽长456 m、宽5 m、高12 m。在水槽的一端为推板式造波机,造波系统采用计算机自动进行调节控制,最大造波能力为3.5 m,造波周期为2~10 s(图 1)。

|
图 1 大比尺波浪水槽 Fig.1 Large scale wave flume |
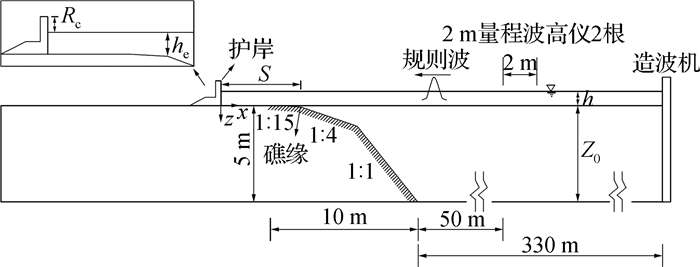
试验采用弗劳德相似准则,按照1: 15的模型比尺进行设计。模型布置如图 2所示,主要包括3个部分:礁前的深水区、礁缘的陡坡区和礁坪平台区。陡坡区的坡度设计值参考Gourlay关于珊瑚礁地形坡度研究中的模型D(Reefs in Malé,Madldives),其中深水区水深5 m,前坡分3段,陡坡坡度为1: 1,1: 4和1: 15。平台上设有直立式护岸,堤顶高0.6 m,顶宽0.15 m,底宽0.9 m。陡坡坡脚与造波机之间的距离为330 m,能较好地复演波浪从深水区经过礁前陡变地形发生破碎,再传播至礁坪上的强非线性物理过程[14]。
|
图 2 试验布置 Fig.2 Experimental arrangement |
试验斜坡和平台采用方钢管和钢板分段焊接而成,试验平台上铺有10 cm厚的混凝土以保持平台高程一致,并且在钢板和水槽壁间隙采用混凝土闭合以防止出现透水现象。水槽墙壁上端布置有6个高速摄像机,用来记录波浪在礁坪上的传播过程。
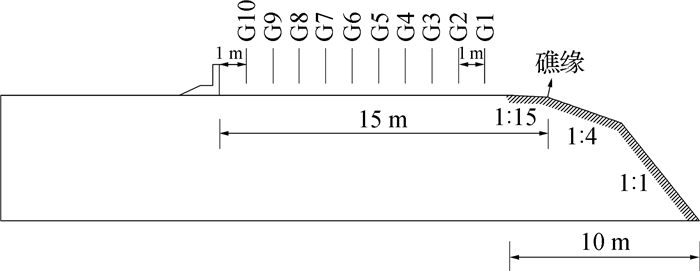
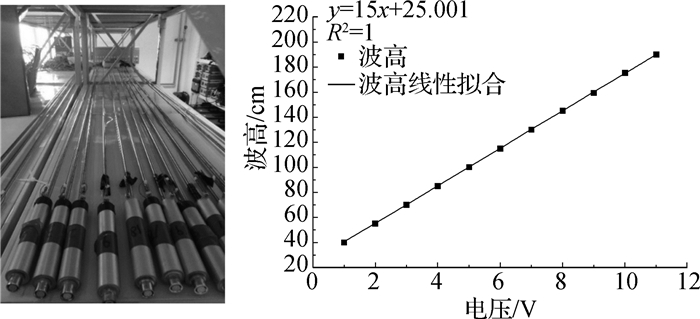
在护岸堤前每隔1 m放置1根波高传感器测量礁坪上的破碎波高,护岸与礁缘之间的距离分为5,10,15和20 m,传感器位置和编号如图 3所示,所有波高传感器均采用电容式波高传感器(图 4)进行采集,传感器精度均为2 mm,率定结果(图 4)表明水位和电压有很好的线性关系。
|
图 3 试验传感器布置(试验地形中护岸离礁缘15 m) Fig.3 Experimental sensor arrangement (revetment is placed 15 m away from the reef edge) |
|
图 4 电容式波高传感器 Fig.4 Capacitive wave height sensor |
试验时的入射波均采用规则波,每种工况重复3次,试验组次共包含3个水位、4个周期、6个入射波波高、护岸与礁缘之间的4个间距和无护岸的情况(如表 1所示),试验波高的原型值可达4.5~12 m,能较好反映极端波浪条件。
| 表 1 试验组次 Tab.1 Experimental group |
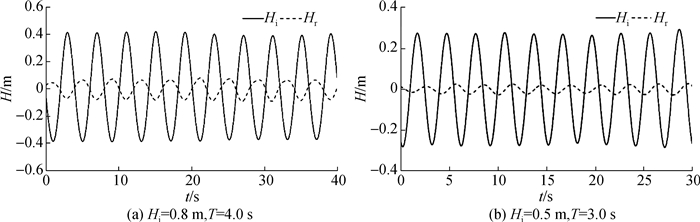
为了提高模拟精度和造波效率,在试验前,首先率定原始波要素。大比尺波浪水槽中的试验制模周期长,为了加快试验进度,波浪的率定在模型安装后进行,此时水槽中的水位变化受到入射波和反射波的共同作用,无法直接得到入射波高。因此,波浪率定时采用入反射分离的方法,先得到准确的入射波高,再通过调整造波机的输入参数,使分离出的入射波的波高和周期满足试验规程要求。试验前,在距水槽边壁2.5 m,距陡坡边缘50 m的深水处布置2根量程2 m的波高传感器测量深水波浪,采用Sun等[17]提出的两点式入反射分离方法,计算得到每组试验的入射波见图 5。
|
图 5 深水处的入射波(Hi)和反射波(Hr)波高 Fig.5 Wave height of incident wave(Hi) and reflected wave(Hr) in deep water |
每组试验开始前均以静水面为零点,试验中在第1个波浪到达深水波高仪时开始采集波高,所有波高传感器通过数据采集系统同步测量,采样频率为50 Hz。为避免试验受到二次反射波的影响,每组试验波浪的采集时间为30个波,均在二次反射波到达前停止采集。每组试验重复3次,最终结果为3次测量数据的平均值,单次间采集数据误差均小于5%,证明试验重复性良好。
2 试验结果与分析 2.1 护岸对波浪形态的影响由于礁坪上存在护岸,会产生反射波,使波浪在礁坪上的破碎更加剧烈。同时,护岸与礁缘之间的距离不同,也会使波浪的破碎和形态变化有所区别。图 6给出了自然条件和护岸建设后极端波浪在礁坪上的传播过程图,从左到右分别为波浪在礁缘发生破碎、在破碎区传播和破碎后继续向内传播。对比发现,护岸建设后的波浪传播形态呈现出如下特征:(1)破波形态仍为激破波,但受护岸的影响,向海运动的反射波与入射波在礁缘斜坡处发生碰撞,礁缘处波峰抬高,引起更偏陡的波面和更强烈的破碎;(2)波浪破碎带更宽,水体掺气更为剧烈;(3)波浪在礁坪上传播的过程中,仍会与反射波发生多次碰撞,使波浪能量的沿程演化十分复杂。

|
图 6 波浪传播形态(红线是波浪破碎带宽度,蓝线为护岸位置,箭头表示波浪传播方向) Fig.6 Wave propagation pattern (Red line is the wave fracture zone width, the blue line is for breakwater, the arrows represent wave propagation direction) |
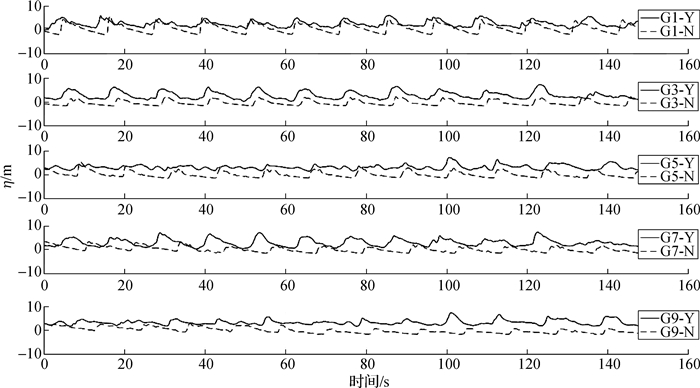
图 7给出了护岸建设前后不同位置处的波面过程线,其中,实线为存在护岸时工况,虚线为自然地形工况。各个测点所在的位置如图 3所示。可以发现,礁坪上的波浪形态以段波为主,即水位上升过程历时短,下降过程历时长。护岸的建设显著增加了礁坪上的水位,且越往礁坪内传播,水位的增加越显著。
|
图 7 不同位置波面过程线(h=3.0 m, Hi=10.7 m, T=11.62 s) Fig.7 Different locations' wave process lines (h=3.0 m, Hi=10.7 m, T=11.62 s) |
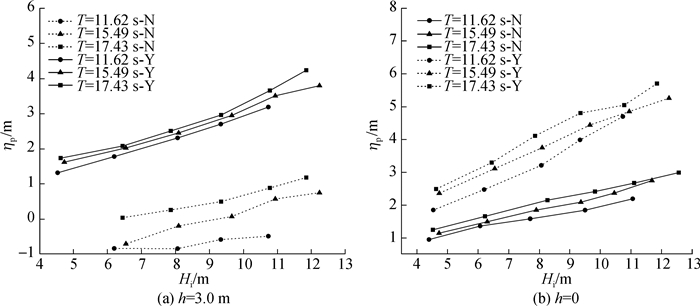
图 8给出了有护岸(S=75 m)和无护岸时的礁坪上最大增水的对比情况。礁坪增水ηp的定义为平均水位与静止水位之间的差值。如图 8(a)所示,当礁坪水深h=3.0 m时,不同周期下的堤前最大增水均大于同条件下无护岸时的礁坪上增水;当礁坪水深减小(h=0 m)时,堤前增水仍大于无护岸时的增水位。这说明护岸的存在阻碍了礁坪波浪和水流的传播,导致礁坪产生了明显的壅水现象。
|
图 8 有护岸(Y,S=150 m)和无护岸(N)时的礁坪最大增水对比 Fig.8 Comparison of the maximum wave setup in reef flat with revetment (Y, S=150 m) and without revetment (N) |
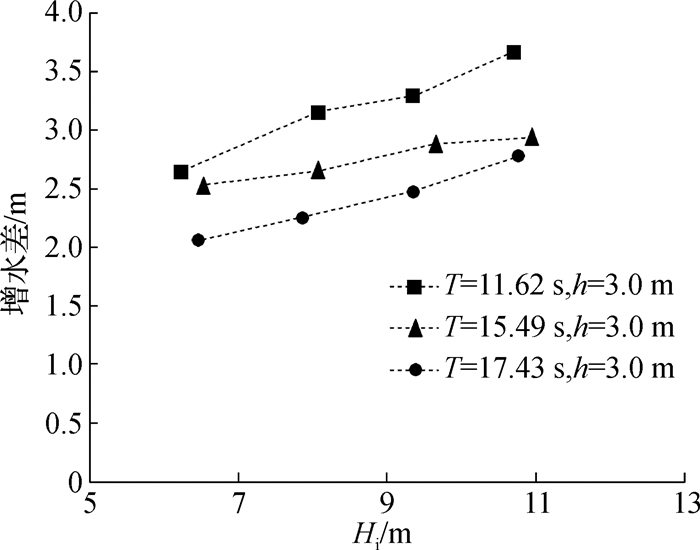
图 9给出了有护岸(Y,S=150 m)和无护岸(N)时不同周期的礁坪增水差值,可以发现,护岸显著增加了礁坪上的增水值,最大增水增加值超过3.5 m,是原来的4倍。这主要是由于护岸的修建使得礁坪上水体在护岸前累积。此外,随着入射波高的增加和波周期的减小,护岸对增水的影响更加显著。
|
图 9 有护岸(Y,S=150 m)和无护岸(N)时不同周期的礁坪增水差值 Fig.9 Differences of water level setup on the reef flat for different wave periods with revetment (Y, S=150 m) and without revetment (N) |
Gourlay提出过估算礁坪时均水位的计算公式[2]:
| $ \frac{\eta_{\mathrm{r}}}{H_{\mathrm{i}}}=0.378 \varepsilon^{2 / 3}\left(\frac{g T^{2}}{H_{\mathrm{i}}}\right)^{1 / 6}\left(\frac{h_{\mathrm{i}}}{H_{\mathrm{i}}}\right)^{1 / 3} $ | (1) |
式中:ηr为礁坪增水;Hi为入射波波高;T为入射波周期;g为重力加速度;hi为深水区水深;ε为由波形决定的无量纲因子(假设波面为正弦波时取1/2π)。
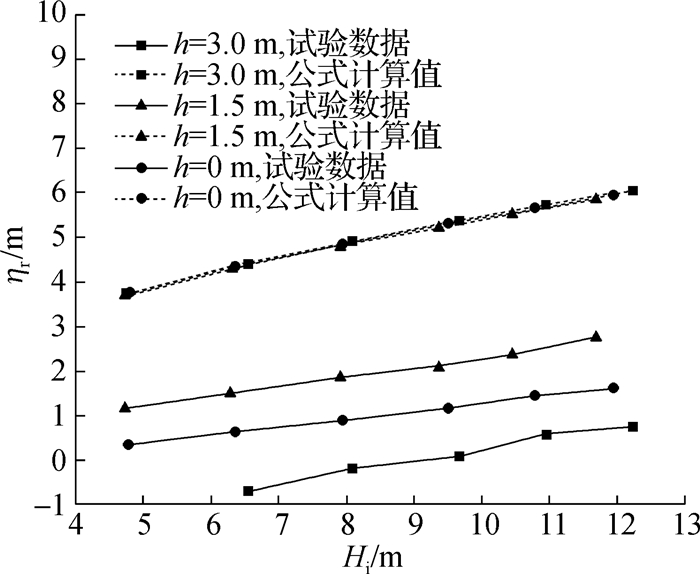
将入射波周期T=15.49 s时礁坪时均水位使用式(1)进行计算,并与试验中的数据进行对比。如图 10所示,很明显在3个不同的礁坪水深下,Gourlay的理论公式计算出的时均水位均大于试验值。当礁坪水深变化时,Gourlay公式计算结果相差较小,这与试验得到的时均水位变化规律明显不符。当礁坪水深h=3 m时,礁坪时均水位会出现低于静水位的情况,主要原因为极端波浪作用下,波浪破碎后产生较大的波生流,一方面使得礁坪上水体被带到后方的泻湖中,另一方面更多的能量转化为水流动能,也使得水位下降,而Gourlay公式不适用于极端波浪和有护岸情况。究其原因,Gourlay公式是基于常浪条件下得到的,且未考虑护岸的影响。而本试验的波浪条件均代表极端情况,波浪在礁缘的破碎更为强烈,叠加上护岸引起的反射波碰撞,导致波浪运动有很大区别。
|
图 10 礁坪最大增水实测值与Gourlay公式计算结果的对比(T=15.49 s) Fig.10 Comparison between measured water maximum increase in reef flat and Gourlay formula (T=15.49 s) |
通过分析相邻波高传感器波面过程线的时间差,计算得到波速C。如图 11所示,相邻的波高传感器WG4和WG5的波面过程线的时间差为dNdt(dN为相邻波高传感器采到波峰时的数据点差值,dt为采样间隔,为0.02 s),其间距为ΔL为1 m,波速C可通过式(2)计算得到:
| $ C=\frac{\Delta L}{\mathrm{d} N \mathrm{d} t} $ | (2) |

|
图 11 相邻波高传感器波面过程线 Fig.11 Water surface elevations from adjacent wave gauges |
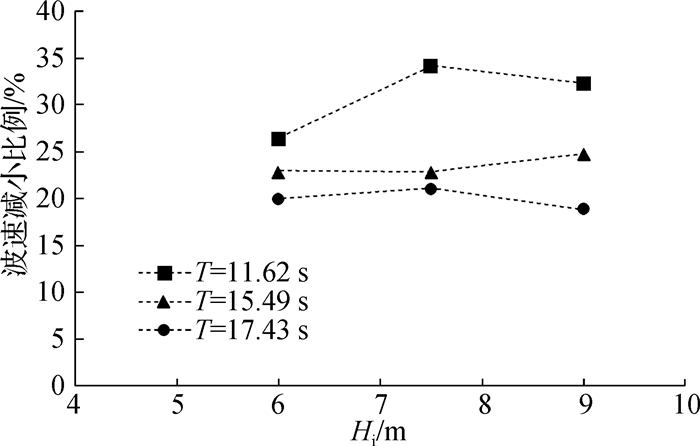
图 12给出了3 m水深条件下,不同入射波高工况下的波速变化规律,图中所示波速为波浪从1号波高仪传到10号波高仪过程中的平均波速。可以看出:①波速随波高的增大而增大,这是典型的浅水区非线性波浪运动特征;②在相同波高下,波速随周期增大而增大,这与浅水波速仅与水深有关的传统认识不一致。虽然礁坪上水深较浅,但由于礁前地形陡变,波浪没有足够的空间发生充分变形以适应于局地水深,因此波速仍在一定程度上受到深水波周期的影响;③由于护岸工程的阻水效应和反射波的影响,礁坪上的波速明显减小。图 13给出了不同工况下护岸引起的波速减小幅度。可以发现,波速的减小幅度为20%~35%,波速的减小受周期影响较大,受入射波高的影响较小。周期越小,护岸对波速的影响程度越大。试验结果还发现,实测的波速量值明显超出线性波理论下的浅水波速公式计算结果。由于超过10 m/s的段波波速会对结构物产生较大的冲击力,上述结果表明采用传统公式会低估珊瑚岛礁护岸工程在极端波浪条件下承受的冲击效应。

|
图 12 不同工况的礁坪上平均波速随入射波高的关系(N:无护岸,Y:有护岸S=150 m) Fig.12 Relationship between average wave celerity and incident wave height on reef flat under different wave conditions (N: no revetment, Y: revetment S=150 m) |
|
图 13 不同工况下护岸对波速的减小程度 Fig.13 Wave celerity reduction under different wave conditions |
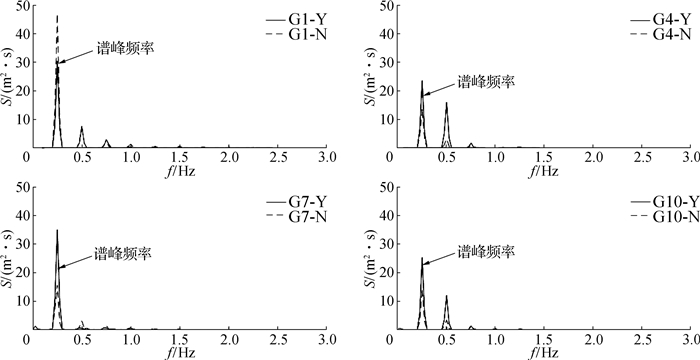
图 14给出了S=150 m时有护岸和无护岸的礁坪上不同位置的波谱。可以看出,不论有无护岸,由于波浪破碎后的非线性相互作用,在主频以外,均产生了高频谐波。无护岸时,主频能量会随着传播距离的增加迅速减小,而护岸的存在使得波浪的非线性相互作用更加复杂。在礁缘位置,反射波与入射波叠加,使得波浪在礁缘处的破碎更加强烈(见图 6),因此能量耗散更多,主频能量更低。随着波浪向礁坪内部传播,主频和高频能量并不会迅速减小,在某些传感器的位置,入反射波叠加的波腹位置主频能量要高于礁缘处,且二阶谐波的能量相对于无防波堤的工况会明显增加。
|
图 14 有护岸(Y,S=150 m)和无护岸(N)珊瑚礁礁坪上不同位置的波谱(h=3.0 m,Hi=6.0 m,T=15.49 s) Fig.14 Comparison of wave spectrums at different locations on coral reef flat with (S=150 m) and without revetment (h =3.0 m, Hi=6.0 m, T=15.49 s) |
珊瑚礁地形上存在护岸时,往往会出现壅水现象,礁坪壅水又会影响防浪建筑物的安全,所以堤前的水位决定了护岸的越浪量大小和护岸结构的稳定性。
图 15给出了护岸与礁缘距离S=150 m时同一礁坪水深h=3.0 m和0时不同周期下的堤前时均水位。可以发现,礁坪水深h=3.0 m,入射波周期不变时,堤前时均水位随着波高的增大而增高;当礁坪水深和波高不变时,堤前时均水位随着周期的增大而增高;当礁坪水深变浅(h=0 m)时,变化趋势与礁坪水深h=3 m的相同,当入射波周期不变,堤前时均水位随着波高的增大而增高;当礁坪水深和波高不变,堤前时均水位随着周期的增大而增高。

|
图 15 S=150 m时不同周期下的堤前时均水位 Fig.15 The average water level before the dike in different periods(S=150 m) |
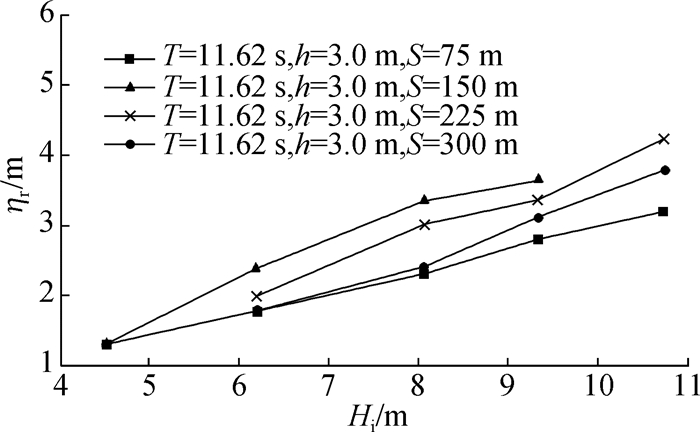
图 16给出了周期T=11.62 s时不同距离下的堤前时均水位。如图 16所示,当礁坪水深h=3.0 m,入射波周期T=11.62 s时,S=75 m的堤前时均水位最低;当S=150 m时,堤前时均水位最大,随后随着距离的增大堤前时均水位有所减小。研究发现出现这种现象是由于护岸离礁缘较近时,波浪与护岸相互作用产生的回流能够流回到深水区,所以堤前时均水位较小,而当护岸与礁缘之间的距离增大到150 m时,礁坪上的回流受阻,水流壅在礁坪上,使礁坪水位整体抬高,从而导致堤前时均水位增高;当护岸与礁缘之间的距离继续增大时,堤前礁坪面积增大,壅高的水位随之减小,使堤前时均水位有所减小。
|
图 16 T=11.62 s,h=3.0 m时不同距离下的堤前时均水位 Fig.16 The average water level in front of the dike at different distances (T=11.62 s and h=3.0 m) |
采用1: 15的模型比尺,从波浪形态、增水、波速、波谱等方面,研究了珊瑚岛礁护岸对礁坪上极端波浪传播特性的影响规律,并分析了护岸距礁缘距离对堤前水位的影响,得到如下结论:
(1) 护岸工程的建设对波浪传播形态具有重要影响,反射波的存在使得礁缘处波浪破碎更为剧烈,波面更为复杂。
(2) 护岸工程产生了明显的阻水效应,显著降低了波速,增加了礁坪增水。波周期越小,阻水效应越明显。
(3) 护岸工程影响了礁坪上的波浪谱分布,使得礁缘处的主频能量更低,但在礁坪上的主频及高频能量均更高。
(4) 护岸距礁缘距离对堤前水位具有重要影响,随着该距离的增加,堤前时均水位呈现先增加后降低的规律。
| [1] |
徐承德, 冯守珍. 岛礁类型划分及可持续发展探讨[J]. 海岸工程, 2008, 27(3): 47-52. ( XU Chengde, FENG Shouzhen. Divisions of island-reef types and discussion on national long-term continued development[J]. Coastal Engineering, 2008, 27(3): 47-52. (in Chinese)) |
| [2] |
GOURLAY M R. Wave set-up on coral reefs. 1. set-up and wave-generated flow on an idealised two dimensional horizontal reef[J]. Coastal Engineering, 1996, 27(3/4): 161-93. |
| [3] |
GOURLAY M R. Wave set-up on coral reefs. 2. set-up on reefs with various profiles[J]. Coastal Engineering, 1996, 28(1/4): 17-55. |
| [4] |
YAO Y, HUANG Z H, MONISMITH S G, et al. Characteristics of monochromatic waves breaking over fringing reefs[J]. Journal of Coastal Research, 2013, 29(1): 94-104. |
| [5] |
YAO Y, ZHANG Q M, CHEN S G, et al. Effects of reef morphology variations on wave processes over fringing reefs[J]. Applied Ocean Research, 2019, 82: 52-62. |
| [6] |
HENCH J L, LEICHTER J J, MONISMITH S G. Episodic circulation and exchange in a wave-driven coral reef and lagoon system[J]. Limnology and Oceanography, 2008, 53(6): 2681-2694. |
| [7] |
MONISMITH S G, HERDMAN L M M, AHMERKAMP S, et al. Wave transformation and wave-driven flow across a steep coral reef[J]. Journal of Physical Oceanography, 2013, 43(7): 1356-1379. |
| [8] |
赵子丹, 张庆河, 刘海青. 波浪在珊瑚礁及台阶式地形上的传播[J]. 海洋通报, 1995, 14(4): 1-10. ( ZHAO Zidan, ZHANG Qinghe, LIU Haiqing. Wave transformation on coral reefs and submerged steps[J]. Marine Science Bulletin, 1995, 14(4): 1-10. (in Chinese)) |
| [9] |
张庆河, 刘海青. 波浪在台阶地形上的破碎[J]. 天津大学学报, 1999, 32(2): 204-207. ( ZHANG Qinghe, LIU Haiqing. Wave breaking on a submerged step[J]. Journal of Tianjin University, 1999, 32(2): 204-207. (in Chinese)) |
| [10] |
SHI J, ZHANG C, ZHENG J H, et al. Modelling wave breaking across coral reefs using a non-hydrostatic model[J]. Journal of Coastal Research, 2018, 85(Suppl1): 501-505. |
| [11] |
姚宇, 杜睿超, 蒋昌波, 等. 礁冠宽度对珊瑚礁坪波浪增水影响的实验研究[J]. 海洋通报, 2017, 36(3): 340-347. ( YAO Yu, DU Ruichao, JIANG Changbo, et al. Experimental study of the effect of reef-crest width on wave-induced set-up over the reef flat[J]. Marine Science Bulletin, 2017, 36(3): 340-347. (in Chinese)) |
| [12] |
任冰, 唐洁, 王国玉, 等. 规则波在岛礁地形上传播变化特性的试验[J]. 科学通报, 2018, 63(5/6): 590-600. ( REN Bing, TANG Jie, WANG Guoyu, et al. Experimental investigation of monochromatic wave transformation characteristics over the coral reefs[J]. Chinese Science Bulletin, 2018, 63(5/6): 590-600. (in Chinese)) |
| [13] |
李绍武, 胡传越, 柳叶. 不规则波在岸礁地形增水变化规律试验[J]. 水科学进展, 2019, 30(4): 581-588. ( LI Shaowu, HU Chuanyue, LIU Ye. Experimental investigation on set-up of irregular waves over fringing reef flat[J]. Advances in Water Science, 2019, 30(4): 581-588. (in Chinese)) |
| [14] |
陈松贵, 张华庆, 陈汉宝, 等. 不规则波在筑堤珊瑚礁上传播的大水槽实验研究[J]. 海洋通报, 2018, 37(5): 576-582. ( CHEN Songgui, ZHANG Huaqing, CHEN Hanbao, et al. Experimental study of irregular wave transformation on reefs with seawalls in large wave flume[J]. Marine Science Bulletin, 2018, 37(5): 576-582. (in Chinese)) |
| [15] |
陈松贵, 陈汉宝, 赵洪波, 等. 珊瑚礁地形上胸墙波浪力大水槽试验[J]. 河海大学学报(自然科学版), 2019, 47(1): 65-70. ( CHEN Songgui, CHEN Hanbao, ZHAO Hongbo, et al. Experimental study of wave forces on the seawall of coral reef in large wave flume[J]. Journal of Hohai University (Natural Sciences), 2019, 47(1): 65-70. (in Chinese)) |
| [16] |
陈松贵, 王泽明, 张弛, 等. 珊瑚礁地形上直立式防浪堤越浪大水槽实验[J]. 科学通报, 2019, 64(增刊2): 3049-3058. ( CHEN Songgui, WANG Zeming, ZHANG Chi, et al. Experimental study on wave overtopping of a vertical seawall on coral reefs in large wave flume[J]. Chinese Science Bulletin, 2019, 64(Suppl2): 3049-3058. (in Chinese)) |
| [17] |
SUN H, WANG Y, PENG J. Hilbert transform applied to separation of waves[J]. China Ocean Engineering, 2002, 16(2): 239-248. |
2. Tianjin Research Institute for Water Transport Engineering, Tianjin 300456, China
 2019
2019 
