2. 合肥工业大学 水资源与环境系统工程研究所, 安徽 合肥 230009
资源环境领域的承载能力概念来源于生态学、用以衡量特定区域中可承载某一物种个体的最大数量[1],随后承载力概念得到扩展并用来说明环境或生态系统承受发展和特定活动能力的限度[2]。水资源承载力是一个国家或地区持续发展过程中各种自然资源承载力的重要组成部分,对一个国家或地区的综合发展具有重要影响[3]。区域水资源承载力综合评价是基于区域水资源承载时空、承载标准、承载原则、承载条件和承载状态等承载要素,从水资源承载的支撑力、压力和调控力3个子系统,建立相应的水资源承载力评价指标体系、评价标准和评价模型,综合评估区域水资源总体状况[4-5]。通过评价区域水资源承载状况,可判断研究区域水资源能否支撑人口、经济与环境协调发展,对水资源超载状况及时提出调控建议,有利于确保水资源-经济社会-生态环境综合体系的协调发展、促进人水和谐发展[6-7]。
经过许多学者深入研究,水资源承载力评价方法已从过去的单指标和静态分析发展到多指标和动态综合分析[8],目前用于水资源承载力评价的主要方法有风险矩阵法[9]、模糊综合评价法[10]、主成分分析法[11]、集对分析法[12]、物元可拓模型[13]、Logistic集对分析模型[14]等。其中,在运用集对分析进行综合评价时,差异度系数I的计算方法是影响其处理不确定性问题的关键,李陶等[15]利用灰色关联[16]的方法求解差异度系数I,李辉等[17]利用联系数的概念评价区域水资源承载力时,差异度系数I仅作为标记。区域水资源承载力评价是对复杂系统的研究,需要考虑多种不确定性因素的相互作用,而集对分析[18]就是研究不确定性问题的一类新颖方法。本文充分考虑水资源系统中众多不确定性因素,通过借鉴灰色关联[16]、减法集对势[4]的思想,深入挖掘集对分析核心思想中各联系数分量间隐含的信息,求解差异度与同一度、对立度之间的偏确定度,从而求解差异度系数I。为此,本文基于全偏确定度的方法,建立区域水资源承载力动态评价模型,同时在安徽省进行实证研究,为区域水资源承载力定量评估奠定科学基础,也为制定有效的区域水资源承载力调控措施提供科学依据。
1 评价方法的构建构建基于全偏确定度的区域水资源承载力动态评价方法有如下9个步骤:
步骤1:在综合分析区域水资源承载力内涵的基础上,依据评价指标体系的全面性、层次性、适用性、可操作性等原则[19-20],依据与区域水资源承载过程相关的影响因素,将区域水资源承载力系统分为承载支撑力、承载压力和承载调控力的3个子系统进一步分解为若干评价指标。3个子系统及其评价指标构成了区域水资源承载力评价指标体系,可描述为{x(k, j)|k=1, 2, 3; j=1, 2, …, nk},其中x(k, j)为某评价区域水资源承载力系统第k子系统中的第j个评价指标,nk是第k子系统中的指标数量,k=1,2,3分别表示支撑力、压力和调控力子系统,评价系统指标总数为n,即n=n1+n2+n3。采用基于加速遗传算法的层次分析法(AGA-AHP)[21-22]计算每个子系统及各指标的权重{wj|j=1, 2, …, n},其中wj为第j个指标的权重,根据最终计算的权重值确定评价指标体系。
步骤2:考虑到区域自然条件、经济和社会等因素对区域水资源承载力的作用,同时,在现有评价指标体系[20]和咨询专家意见的基础上,建立区域水资源承载力评价等级标准{s(g, j)|g=1, 2, …, G; j=1, 2, …, n},相应的评价指标样本数据集记为{x(i, k, j)| i=1, 2, …, N; k=1, 2, 3; j=1, 2, …, n}。其中G,N分别为评价等级标准的等级数和评价区域总数。为简便且不失一般性,这里的水资源承载力评价指标采用3个等级标准[23],其中1级、2级、3级分别表示未超载、临界超载、超载。
步骤3:计算评价区域i水资源承载力的第k子系统的第j个评价指标样本值{x(i, k, j)| i=1, 2, …, N; k=1, 2, 3; j=1, 2, …, nk}与水资源承载力评价等级标准{s(g, j)|g=1, 2, 3; j=1, 2, …, nk}之间的评价指标值联系数{u1g(i, k, j)| i=1, 2, …, N; k=1, 2, 3; j=1, 2, …, nk},u1g(i, k, j)=a1g(i, k, j)+b1g(i, k, j)I+c1g(i, k, j)J。评价区域i水资源承载力第k子系统的第j个评价指标联系数[18, 24]。
| $ {a_1}\left( {i,k,j} \right) = \left\{ \begin{array}{l} 1,\;正向指标\;x\left( {i,k,j} \right) \le s\left( {1,j} \right)或反向指标\;x\left( {i,k,j} \right) \ge s\left( {1,j} \right)\\ 1 - 2\frac{{x\left( {i,k,j} \right) - s\left( {1,j} \right)}}{{s\left( {2,j} \right) - s\left( {1,j} \right)}},正向指标\;s\left( {1,j} \right) < {x_{ij}} \le s\left( {2,j} \right)\;或反向指标\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;s\left( {i,1,j} \right) > x\left( {i,k,j} \right) \ge s\left( {2,j} \right)\\ - 1,正向指标\;x\left( {i,k,j} \right) > s\left( {2,j} \right)\;或反向指标\;x\left( {i,k,j} \right) \ge s\left( {2,j} \right) \end{array} \right. $ | (1) |
| $ {b_1}\left( {i,k,j} \right) = \left\{ \begin{array}{l} 1 - 2\frac{{s\left( {1,j} \right) - x\left( {i,k,j} \right)}}{{s\left( {1,j} \right) - s\left( {0,j} \right)}},正向指标\;x\left( {i,k,j} \right) \le s\left( {1,j} \right)\;或反向指标\;x\left( {i,k,j} \right) \ge s\left( {1,j} \right)\\ 1,正向指标\;s\left( {1,j} \right) < x\left( {i,k,j} \right) \le s\left( {2,j} \right)\;或反向指标\;s\left( {1,j} \right) > x\left( {i,k,j} \right) \ge s\left( {2,j} \right)\\ 1 - 2\frac{{x\left( {i,k,j} \right) - s\left( {2,j} \right)}}{{s\left( {3,j} \right) - s\left( {2,j} \right)}},正向指标\;s\left( {2,j} \right) < x\left( {i,k,j} \right) \le s\left( {3,j} \right)\;或反向指标\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{s_{2j}} > x\left( {i,k,j} \right) \ge {s_{3j}}\\ - 1,正向指标\;x\left( {i,k,j} \right) > s\left( {3,j} \right)或反向指标\;x\left( {i,k,j} \right) < s\left( {3,j} \right) \end{array} \right. $ | (2) |
| $ {c_1}\left( {i,k,j} \right) = \left\{ \begin{array}{l} - 1,正向指标\;x\left( {i,k,j} \right) \le s\left( {1,j} \right)或反向指标\;x\left( {i,k,j} \right) \ge s\left( {1,j} \right)\\ 1 - 2\frac{{s\left( {2,j} \right) - x\left( {i,k,j} \right)}}{{s\left( {2,j} \right) - s\left( {1,j} \right)}},正向指标\;s\left( {1,j} \right) < x\left( {i,k,j} \right) \le s\left( {2,j} \right)或反向指标\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;s\left( {1,j} \right) > x\left( {i,k,j} \right) \ge s\left( {2,j} \right)\\ 1,正向指标\;s\left( {2,j} \right) < x\left( {i,k,j} \right) \le s\left( {3,j} \right)或反向指标\;s\left( {2,j} \right) > x\left( {i,k,j} \right) \ge s\left( {3,j} \right) \end{array} \right. $ | (3) |
式中:正向指标表示标准等级随评价指标值的增大而增大,反向指标表示标准等级值随评价指标值的增大而减小;s(0, j)是每个指标等级1的评价级别的另一端点值,s(1, j)为1级与2级评价标准之间的阈值,s(2, j)是2级与3级评价标准之间的阈值,s(3, j)是每个指标等级3的评价级别的另一端点值[24]。
步骤4:将同一度、差异度与对立度转化成相对隶属度[4]并归一化。
| $ \left\{ \begin{array}{l} a_2^*\left( {i,k,j} \right) = 0.5 + 0.5{a_1}\left( {i,k,j} \right)\\ b_2^*\left( {i,k,j} \right) = 0.5 + 0.5{b_1}\left( {i,k,j} \right)\\ c_2^*\left( {i,k,j} \right) = 0.5 + 0.5{c_1}\left( {i,k,j} \right) \end{array} \right. $ | (4) |
| $ \left\{ \begin{array}{l} {a_2}\left( {i,k,j} \right) = \frac{{a_2^*\left( {i,k,j} \right)}}{{a_2^*\left( {i,k,j} \right) + b_2^*\left( {i,k,j} \right) + c_2^*\left( {i,k,j} \right)}}\\ {b_2}\left( {i,k,j} \right) = \frac{{b_2^*\left( {i,k,j} \right)}}{{a_2^*\left( {i,k,j} \right) + b_2^*\left( {i,k,j} \right) + c_2^*\left( {i,k,j} \right)}}\\ {c_2}\left( {i,k,j} \right) = \frac{{c_2^*\left( {i,k,j} \right)}}{{a_2^*\left( {i,k,j} \right) + b_2^*\left( {i,k,j} \right) + c_2^*\left( {i,k,j} \right)}} \end{array} \right. $ | (5) |
步骤5:构造被评价区域i水资源承载力评价样本联系数u2gi。用集对分析方法[12, 18]将评价区域i与标准等级g之间进行集对,得到联系数u2gi,例如,当评价区域i与等级1集对时,联系数[18, 25]为:
| $ {u_{2,1}}\left( {i,k,j} \right) = {a_{2,1}}\left( {i,k,j} \right) + {b_{2,1}}\left( {i,k,j} \right)I + {c_{2,1}}\left( {i,k,j} \right)J $ | (6) |
| $ {u_{2,1}}\left( {i,k} \right) = {a_{2,1}}\left( {i,k} \right) + {b_{2,1}}\left( {i,k} \right)I + {c_{2,1}}\left( {i,k} \right)J $ | (7) |
| $ {u_{2,1,i}} = {a_{2,1,i}} + {b_{2,1,i}}I + {c_{2,1,i}}J $ | (8) |
式中:
式(7)~(8)中,u2, 1(i, k)为评价区域i中水资源承载力第k子系统与标准等级g之间集对得到的三元联系数,a2, 1(i, k)为第k子系统属于集对等级1所有a2,1(i, k, j)指标进行权重加和,b2, 1(i, k)为第k子系统属于集对等级1相邻等级所有b2,1(i, k, j)的权重加和,c2, 1(i, k)为第k子系统属于与集对等级1相隔等级所有c2,1(i, k, j)的权重加和。a2, 1, i为评价区域i的3个子系统中属于集对等级1所有a1(i, k)进行加和,同理得b2, 1, i和c2, 1, i。u2, 1, i为评价区域i与等级1之间集对时的联系数,I为差异度系数,J为对立度系数。
步骤6:归一化式(7)和(8)的同一度、差异度、对立度[4],得到评价区域i的第k子系统联系数ug(i, k)和评价区域i的三元联系数ugi。
| $ \left\{ \begin{array}{l} {a_g}\left( {i,k} \right) = \frac{{{a_{2g}}\left( {i,k} \right)}}{{{a_{2g}}\left( {i,k} \right) + {b_{2g}}\left( {i,k} \right) + {c_{2g}}\left( {i,k} \right)}}\\ {a_{gi}} = \frac{{{a_{2gi}}}}{{{a_{2gi}} + {b_{2gi}} + {c_{2gi}}}}\\ {b_g}\left( {i,k} \right) = \frac{{{b_{2g}}\left( {i,k} \right)}}{{{a_{2g}}\left( {i,k} \right) + {b_{2g}}\left( {i,k} \right) + {c_{2g}}\left( {i,k} \right)}}\\ {b_{gi}} = \frac{{{b_{2gi}}}}{{{a_{2gi}} + {b_{2gi}} + {c_{2gi}}}}\\ {c_g}\left( {i,k} \right) = \frac{{{c_{2g}}\left( {i,k} \right)}}{{{a_{2g}}\left( {i,k} \right) + {b_{2g}}\left( {i,k} \right) + {c_{2g}}\left( {i,k} \right)}}\\ {c_{gi}} = \frac{{{c_{2gi}}}}{{{a_{2gi}} + {b_{2gi}} + {c_{2gi}}}} \end{array} \right. $ | (9) |
| $ {u_g}\left( {i,k} \right) = {a_g}\left( {i,k} \right) + {b_g}\left( {i,k} \right)I + {c_g}\left( {i,k} \right)J $ | (10) |
| $ {u_{gi}} = {a_{gi}} + {b_{gi}}I + {c_{gi}}J $ | (11) |
步骤7:计算偏确定度。灰色关联[16]与减法集对势方法[4]相结合,将减法集对势的思想用于灰色关联的数列关系求解中。首先要确定主数列与副数列,将差异度bgi作为主数列,同一度agi、对立度cgi分别作为副数列, 其中bgi是不同评价样本i与等级g集对时的差异度值,同理得agi,cgi。记bgi与agi的偏正确定系数ξbgiagi,计算式[4, 12]为:
| $ {\xi _{{b_{gi}}{a_{gi}}}} = {a_{gi}}\left( {1 + {b_{gi}}} \right) $ | (12) |
于是bgi与agi之间的偏正确定度rbgiagi为:
| $ {r_{{b_{gi}}{a_{gi}}}} = \frac{1}{N}\sum\limits_{i = 1}^N {{\xi _{{b_{gi}}{a_{gi}}}}} $ | (13) |
式中:rbgiagi为主数列bgi与副数列agi之间的偏正确定度,是所有偏正确定系数ξbgiagi的算术平均值。同理,参照式(12)~(13)可得bgi与cgi的偏负确定度rbgicgi。
步骤8:确定差异度系数I。将步骤7得到的偏正确定度rbgiagi、偏负确定度rbgicgi归一化处理,得到r′ bgiagi和r′ bgicgi,将差异度系数I按比例分为r′ bgiagi与-r′ bgicgi两个部分[26],以此得到评价样本的联系度值:
| $ {u_{gi}} = {a_{gi}} + {b_{gi}}\left( {{{r'}_{{b_{gi}}{a_{gi}}}} - {{r'}_{{b_{gi}}{c_{gi}}}}} \right) + {c_{gi}}J $ | (14) |
式中:(r′ bgiagi-r′ bgicgi)为全偏确定度。运用式(14)对差异度系数I的分配方法,依据同一度、对立度比例将bgiI分成两部分,用联系数的伴随函数减法集对势[4]的思路分配差异度系数I,以此减少差异度系数I取值上的不确定性,同时,进一步挖掘了集对分析中同一度、差异度、对立度之间隐含的关系。
步骤9:评价样本i的水资源承载力等级。通过归一化式(14)计算的联系度值得评价样本i的联系数vgi,样本i隶属于模糊集“标准等级g”的相对隶属度vgi*可表示为[24]:
| $ v_{gi}^ * = 0.5 + 0.5{u_{gi}} $ | (15) |
进行归一化运算,得到评价样本i的联系数vgi:
| $ {v_{gi}} = v_{gi}^*/\sum\limits_{g = 1}^G {v_{gi}^*} $ | (16) |
采用级别特征值法[27]计算样本i的等级值Hi:
| $ {H_i} = \sum\limits_{g = 1}^G {{v_{gi}}} \cdot g $ | (17) |
为了比较分析级别特征值法的评价结果,提高水资源承载力结果的合理性,同时采用属性识别法[28]评价区域i的水资源承载力评价等级值gi:
| $ {g_i} = \left\{ \begin{array}{l} 1,{v_{1i}} > \lambda \\ 2,{v_{1i}} \le \lambda \;且\;{v_{1i}} + {v_{2i}} > \lambda \\ 3,{v_{1i}} + {v_{2i}} \le \lambda \;且\;{v_{1i}} + {v_{2i}} + {v_{3i}} > \lambda \end{array} \right. $ | (18) |
式中:λ表示置信度,通常为[0.50, 0.70],λ越大表示评价结果越趋于稳妥[28],本文取λ=0.50[17]。
2 实例分析以安徽省16个地市为研究区域,为深入探讨安徽省水资源承载驱动机制,参考《安徽省城镇体系规划2011—2030》和淮河、长江流域,将安徽省16个地市分为3个研究区:淮河以北的皖北地区(淮北、亳州、宿州、蚌埠、阜阳、淮南6个城市),长江、淮河之间的皖中地区(合肥、滁州、六安、安庆4个城市),长江以南的皖南地区(马鞍山、芜湖、宣城、铜陵、池州、黄山6个城市)。依照《安徽省统计年鉴》(2012—2016年)和《安徽省水资源公报》(2011—2015年)的资料,运用上述评价模型对2011—2015年安徽省水资源现状进行综合评价。由步骤1得到评价等级标准及权重,结果见表 1[17]。
| 表 1 安徽省水资源承载力评价指标、等级标准及权重[17] Tab.1 Standard and weight of index of water resources carrying capacity in Anhui Province[17] |
从《安徽省水资源公报》、《安徽省统计年鉴》和《安徽省水资源综合规划文本》中收集整理2011—2015年安徽省16个地级市各评价指标的数据及相关资料,由式(1)~(18)对安徽省水资源承载力进行综合评价,因篇幅有限,只将2015年安徽省的水资源承载力计算结果进行展示,见表 2。
| 表 2 2015年安徽省16个地市联系数及其评价等级 Tab.2 Connection number and evaluation grade of 16 cities in Anhui Province in 2015 |
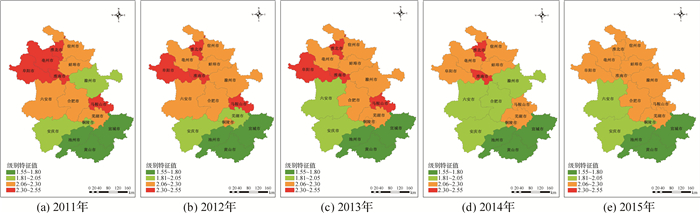
为进一步分析安徽省水资源承载力空间上的差异,用级别特征值和属性识别从水资源承载力子系统层面对安徽省各地市进行评价分析,并按级别特征值法计算得到的评价等级值绘图,如图 1所示。
|
图 1 2011—2015年安徽省16个地市水资源承载力时空分布 Fig.1 Spatial-temporal distribution of water resources carrying capacity in 16 cities of Anhui Province from 2011 to 2015 |
由图 1可知:(1)从时间上可看出安徽省水资源承载状况趋于向好,2011年全省评价等级为2.126,到2015年时达到2.049,降低了0.079。但是水资源承载状况依然处在临界超载状态,全省5年间基本处在2.0左右,水资源形势依然不乐观。从空间上来看,安徽省南北差异明显,由北向南水资源承载状况逐渐趋好,皖北水资源状况最差。(2)从安徽省3个地区的变化趋势可以看出,皖北水资源承载状况始终处在超载的边缘,亟需安徽省出台相关的措施进行治理,改变当前的发展模式。皖中水资源承载状况5年间基本处在承载临界状态,没有发生较为明显的改观,此地区还需进一步加强水资源的开发利用效率。皖南地区是全省水资源承载状况最好的地区,多年平均承载力等级稳定在1.9左右。(3)从安徽省3个地区的典型地市的变化趋势可以看出,皖北中阜阳市由2011年的2.423降到2015年的2.177,呈现出较好的发展趋势,但是仍处在超载的边缘,是皖北变化趋势的典型代表。皖中的合肥市由2011年的2.258降到2014年的2.032最后到2015年的2.175,承载力等级先降后升,始终处在临界超载状况。皖南中池州市、黄山市和宣城市始终处在未超载状态,发展状况一直较好,而芜湖市和马鞍山市一直处在临界超载状态,没有发生较为明显的改观。
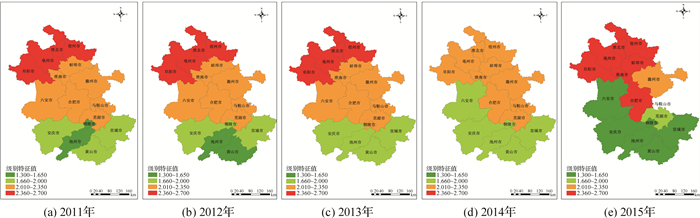
为进一步分析安徽省水资源承载力的变化如何受3个子系统的影响以及子系统与整体之间的相互作用关系,由式(1)~(18)计算2011—2015年间安徽省16个地级市的水资源支撑力、压力、调控力评价结果并分别绘图进行分析,如图 2~4所示。
|
图 2 2011—2015年安徽省16个地市水资源承载支撑力时空分布 Fig.2 Spatial and temporal distribution of water resources support capacity in 16 cities of Anhui Province from 2011 to 2015 |
|
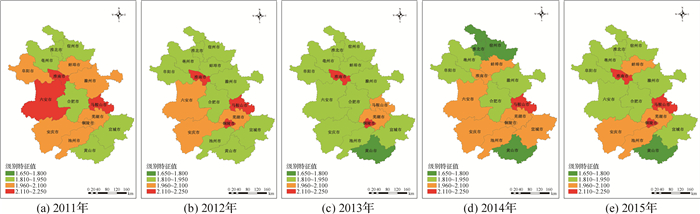
图 3 2011—2015年安徽省16个地市水资源承载压力时空分布 Fig.3 Spatial-temporal distribution of water resources carrying pressure in 16 cities of Anhui Province from 2011 to 2015 |
|
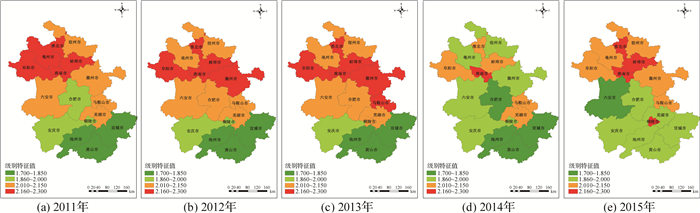
图 4 2011—2015年安徽省16个地市水资源承载调控力时空分布 Fig.4 Spatial and temporal distribution of water resources control capacity in 16 cities of Anhui Province from 2011 to 2015 |
由图 2可知:(1) 2011—2015年间安徽省水资源承载支撑力评价等级处在2.1左右,保持在相对稳定的状态,这与全省整体评价等级基本一致,从北到南支撑力呈明显的变化,皖北支撑力等级较大,皖中处在过渡阶段,皖南支撑力等级较小。从空间上来看,安徽省南北差异明显,由北向南水资源承载支撑力逐渐趋好,皖北水资源支撑力状况最差。(2)从安徽省3个地区的支撑力等级变化可以看出,皖北在2014年的评价达到2.279,处于最好状况,2015年等级增长至2.601,达到历史最高等级,皖北支撑力始终处在一个高位,即使稍有降低,依然没有彻底改变超2.0的状况。皖中2011—2013年基本没有变化,在2014年出现转好的趋势,2015年达到最好状况,最终整个地区支撑力等级达到1.939。皖南在2011—2015年间处在向好的趋势,支撑力等级从2011的1.885降低到2015年的1.619,全地区评价等级降低了0.265。(3)从安徽省3个地区的典型地市的变化趋势可以看出,皖北地区中淮南市和蚌埠市在5年间等级分别增长了0.274和0.265,2015年时分别达到2.494和2.478,支撑力处在较差的状况,是全区典型的发展趋势。皖中地区中六安市、安庆市支撑力等级变化较为明显,5年间分别提升了0.473和0.401,而合肥市由2011年的2.185增长了0.256。皖南地区中黄山市和宣城市发生较为明显的改观,分别由2011年的1.765和1.784降低至1.419和1.333,如此大的降幅在全省均属少见。
由图 3可知:(1)安徽省整体从时间上来看,水资源承载压力在2011—2014年间评级等级趋于向好,评价等级降低了0.091,全省在2014年时水资源压力等级达到最低,为1.913。空间上皖中大部、皖南大部压力状态在2015年时不容乐观,皖北压力状况进一步缓解。(2)皖北水资源压力相对较小,且每年的发展趋势向好,评价由2011年的1.961降至2015年的1.862。皖中地区水资源压力最高等级由2011年逐渐降低至2014年的1.861,2015年时向好趋势稍有回落,增至1.929。皖南地区水资源压力等级稳定在2.0左右,皖南南部普遍高于北部,压力等级有逐渐增加的趋势。(3)从安徽省3个地区的典型地市的变化趋势可以看出,皖北地区中宿州市变化最为明显,水资源压力等级降低了0.176,蚌埠市和淮南市水资源压力状况不容乐观,一直处于高位。皖中地区中合肥市和滁州市水资源压力始终保持在1.9左右,其他地市有较为明显的波动,每年压力状况不平稳。皖南地区中黄山市压力等级维持在1.8左右,处在较好水平,马鞍山市压力等级多年普遍高于2.15,是此地区压力问题突出地市。
由图 4可知:(1)从时间上可以看出安徽省水资源承载调控力,2011—2015年间全省水资源调控力保持在2.0左右,未出现较大波动。全省2014年时达到最佳状况,水资源调控能力整体最好,达到1.953。空间上呈现出南北较大差异,皖北水资源调控能力明显弱于皖南。(2)从全省3个地区可以看出,皖北水资源调控力等级在5年间趋好,2013年等级最高,为2.181,2014年评价等级最低,为2.052。皖中水资源承载力等级由2011年的2.028降低至2015年的1.922,全区处于较好的发展态势,从图 4可以看出,皖中处于皖北与皖南的过渡区域。皖南水资源调控力等级始终处于较好的水平,是全省调控力等级最好的地区,全区整体等级在1.9左右,2014年达到1.885,是历年最好水平,皖南是全省其他地市借鉴的模范,好的整治措施应当积极推广。(3)从安徽省3个地区的典型地市的变化趋势可以看出,皖北地区中亳州市水资源调控力有较大改善,由2011年的2.157提升至2014年的1.983,2015年时趋于2.043,这样的变化趋势是皖北地区整体变化的缩影。皖中地区滁州市是波动较大的一个城市,评价等级最高为2.207,最低为1.965,合肥市由超2级水平逐渐回落到2级以下,最终为1.867。皖南地区中铜陵市的调控力评价等级由2011年的1.976变化到2015年的2.190,呈现出调控力减弱的趋势,应当采取相应的措施。皖南地区中池州市、黄山市和宣城市在2011—2014年间基本在1.8左右徘徊,2015年时增长了0.06,但依然小于2,是全省调控力状况较好的3个城市。
3 结语本文构建基于全偏确定度的区域水资源承载力时空动态评价方法,并在安徽省进行了实证研究,分析出安徽省水资源承载力现状及16个地市的水资源承载力现状,同时分析了水资源承载力3个子系统的评价等级的时空分布,得到了这3个子系统与整体评价结果的关系。结果表明:
(1) 运用同一度、差异度、对立度三者之间的模糊关系信息,求解同一度与差异度、对立度与差异度之间的全偏确定度,从而改进差异度系数的分配方式,实际运用的结果与安徽省水资源承载实际情况基本一致,表明对差异度系数I的取值方式是合理可靠的,充分挖掘出联系数隐含的信息。
(2) 安徽省水资源承载力状况有向好趋势,但是仍然处于临界超载状态,由北往南有着明显的地区差别,其中皖北地区水资源形势处在超载状态,前景不容乐观,皖中地区水资源形势处在临界超载状态,皖南地区水资源形势处在未超载状态。水资源支撑力等级值方面皖北较大,皖南中等,皖北最小;压力方面皖北、皖南较小,皖中较大; 调控力方面皖北较大,皖中、皖南较小。
(3) 安徽省皖北水资源承载力处在超载状态,主要由于该地区水资源支撑力、调控力较小,且压力较大,导致最终的水资源形势不乐观。皖中水资源承载力处在临界超载状态,主要由于3个子系统相对均衡,且3个系统等级值均较高。皖南水资源承载力处在未超载状态,主要是由于水资源调控力、支撑力较大,压力较小,水资源承载力状况全省最好。
| [1] |
孙鸿烈. 中国资源科学百科全书[M]. 北京: 中国大百科全书出版社, 2000. ( SUN Honglie. China encyclopedia of resources science[M]. Beijing: China Encyclopedia Publishing House, 2000. (in Chinese))
|
| [2] |
冯尚友. 水资源持续利用与管理导论[M]. 北京: 科学出版社, 2000. ( FENG Shangyou. Introduction to sustainable utilization of water resources[M]. Beijing: Science Press, 2000. (in Chinese))
|
| [3] |
汤奇成, 张捷斌. 西北干旱地区水资源与生态环境保护[J]. 地理科学进展, 2001, 20(3): 227-233. ( TANG Qicheng, ZHANG Jiebin. Water resources and eco-environment protection in the arid regions in Northwest of China[J]. Progress in Geography, 2001, 20(3): 227-233. (in Chinese)) |
| [4] |
金菊良, 沈时兴, 郦建强, 等. 基于联系数的区域水资源承载力评价与诊断分析方法[J]. 华北水利水电大学学报(自然科学版), 2018, 39(1): 1-9. ( JIN Juliang, SHEN Shixing, LI Jianqiang, et al. Assessment and diagnosis analysis method for regional water resources carrying capacity based on connection number[J]. Journal of North China University of Water Resources and Electric Power (Natural Science Edition), 2018, 39(1): 1-9. (in Chinese)) |
| [5] |
吴开亚, 金菊良, 魏一鸣, 等. 基于指标体系的流域水安全诊断评价模型[J]. 中山大学学报(自然科学版), 2008, 47(4): 105-113. ( WU Kaiya, JIN Juliang, WEI Yiming, et al. Diagnosis assessment model of watershed water security based on index system[J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2008, 47(4): 105-113. (in Chinese)) |
| [6] |
REN C F, GUO P, LI M, et al. An innovative method for water resources carrying capacity research—Metabolic theory of regional water resources[J]. Journal of Environmental Management, 2016, 167: 139-146. |
| [7] |
HARRIS J M, KENNEDY S. Carrying capacity in agriculture: global and regional issues[J]. Ecological Economics, 1999, 29(3): 443-461. |
| [8] |
张永勇, 夏军, 王中根. 区域水资源承载力理论与方法探讨[J]. 地理科学进展, 2007, 26(2): 126-132. ( ZHANG Yongyong, XIA Jun, WANG Zhonggen. Research on regional water resources carrying capacity theory and method[J]. Progress in Geography, 2007, 26(2): 126-132. (in Chinese)) |
| [9] |
金菊良, 董涛, 郦建强, 等. 区域水资源承载力评价的风险矩阵方法[J]. 华北水利水电大学学报(自然科学版), 2018, 39(2): 46-50. ( JIN Juliang, DONG Tao, LI Jianqiang, et al. Risk matrix method for evaluating regional water resources carrying capacity[J]. Journal of North China University of Water Resources and Electric Power (Natural Science Edition), 2018, 39(2): 46-50. (in Chinese)) |
| [10] |
MENG L H, CHEN Y N, LI W H, et al. Fuzzy comprehensive evaluation model for water resources carrying capacity in Tarim River Basin, Xinjiang, China[J]. Chinese Geographical Science, 2009, 19(1): 89-95. |
| [11] |
MOSLEY L M, ZAMMIT B, LEYDEN E, et al. The impact of extreme low flows on the water quality of the Lower Murray River and Lakes (South Australia)[J]. Water Resources Management, 2012, 26(13): 3923-3946. |
| [12] |
金菊良, 张浩宇, 宁少尉, 等. 效应全偏联系数及其在区域水资源承载力评价中的应用[J]. 华北水利水电大学学报(自然科学版), 2019, 40(1): 1-8. ( JIN Juliang, ZHANG Haoyu, NING Shaowei, et al. Effect full partial connection number and its application in evaluation of regional water resources carrying capacity[J]. Journal of North China University of Water Resources and Electric Power (Natural Science Edition), 2019, 40(1): 1-8. (in Chinese)) |
| [13] |
左其亭, 张培娟, 马军霞. 水资源承载能力计算模型及关键问题[J]. 水利水电技术, 2004, 35(2): 5-8, 11. ( ZUO Qiting, ZHANG Peijuan, MA Junxia. Calculating model and key questions about carrying capacity of water resources[J]. Water Resources and Hydropower Engineering, 2004, 35(2): 5-8, 11. (in Chinese)) |
| [14] |
刘童, 杨晓华, 宋帆. 水资源承载力评价的Logistic集对分析模型及其应用[J]. 华北水利水电大学学报(自然科学版), 2019, 40(1): 27-33. ( LIU Tong, YANG Xiaohua, SONG Fan. Logistic set pair analysis model for water resources carrying capacity assessment and its application[J]. Journal of North China University of Water Resources and Electric Power (Natural Science Edition), 2019, 40(1): 27-33. (in Chinese)) |
| [15] |
李陶, 付强, 丁红. 基于灰色关联度的集对分析差异系数研究[J]. 黑龙江水专学报, 2010, 37(1): 97-99. ( LI Tao, FU Qiang, DING Hong. Research for variation coefficient in set pair analysis based on correlation degree of grey theory[J]. Journal of Heilongjiang Hydraulic Engineering, 2010, 37(1): 97-99. (in Chinese)) |
| [16] |
邓聚龙. 灰色系统理论教程[M]. 武汉: 华中理工大学出版社, 1990. ( DENG Julong. Course of grey system theory[M]. Wuhan: Huazhong University of Science and Technology Press, 1990. (in Chinese))
|
| [17] |
李辉, 金菊良, 吴成国, 等. 基于联系数的安徽省水资源承载力动态诊断评价研究[J]. 南水北调与水利科技, 2018, 16(1): 42-49. ( LI Hui, JIN Juliang, WU Chengguo, et al. Dynamic evaluation and diagnostic analysis for water resources carrying capacity in Anhui province based on connection number[J]. South-to-North Water Transfers and Water Science & Technology, 2018, 16(1): 42-49. (in Chinese)) |
| [18] |
赵克勤. 集对分析及其初步应用[M]. 杭州: 浙江科技出版社, 2000. ( ZHAO Keqin. Set pair analysis and its application[M]. Hangzhou: Zhejiang Science and Technology Press, 2000. (in Chinese))
|
| [19] |
SONG X M, KONG F Z, ZHAN C S. Assessment of water resources carrying capacity in Tianjin City of China[J]. Water Resources Management, 2011, 25(3): 857-873. |
| [20] |
王友贞, 施国庆, 王德胜. 区域水资源承载力评价指标体系的研究[J]. 自然资源学报, 2005, 20(4): 597-604. ( WANG Youzhen, SHI Guoqing, WANG Desheng. Study on evaluation indexes of regional water resources carrying capacity[J]. Journal of Natural Resources, 2005, 20(4): 597-604. (in Chinese)) |
| [21] |
金菊良, 洪天求, 王文圣. 基于熵和FAHP的水资源可持续利用模糊综合评价模型[J]. 水力发电学报, 2007, 26(4): 22-28. ( JIN Juliang, HONG Tianqiu, WANG Wensheng. Entropy and FAHP based fuzzy comprehensive evaluation model of water resources sustaining utilization[J]. Journal of Hydroelectric Engineering, 2007, 26(4): 22-28. (in Chinese)) |
| [22] |
金菊良, 沈时兴, 陈梦璐, 等. 遗传层次分析法在区域水资源承载力评价指标体系筛选中的应用[J]. 华北水利水电大学学报(自然科学版), 2019, 40(2): 1-6, 15. ( JIN Juliang, SHEN Shixing, CHEN Menglu, et al. Application of genetic analytic hierarchy process in screening the evaluation index system of regional water resources carrying capacity[J]. Journal of North China University of Water Resources and Electric Power (Natural Science Edition), 2019, 40(2): 1-6, 15. (in Chinese)) |
| [23] |
CUI Y, FENG P, JIN J L, et al. Water resources carrying capacity evaluation and diagnosis based on set pair analysis and improved the entropy weight method[J]. Entropy, 2018, 20(5): 359. |
| [24] |
金菊良, 吴开亚, 魏一鸣. 基于联系数的流域水安全评价模型[J]. 水利学报, 2008, 39(4): 401-409. ( JIN Juliang, WU Kaiya, WEI Yiming. Connection number based assessment model for watershed water security[J]. Journal of Hydraulic Engineering, 2008, 39(4): 401-409. (in Chinese)) |
| [25] |
王文圣, 金菊良, 丁晶, 等. 水资源系统评价新方法——集对评价法[J]. 中国科学(E辑):技术科学, 2009, 52(9): 3017-3023. ( WANG Wensheng, JIN Juliang, DING Jing, et al. A new approach to water resources system assessment―set pair analysis method[J]. Science in China(SerE): Technological Sciences, 2009, 52(10): 3017-3023. (in Chinese)) |
| [26] |
金菊良, 张浩宇, 陈梦璐, 等. 基于灰色关联度和联系数耦合的农业旱灾脆弱性评价和诊断研究[J]. 灾害学, 2019, 34(1): 1-7. ( JIN Juliang, ZHANG Haoyu, CHEN Menglu, et al. Evaluation and diagnosis of agricultural drought vulnerability based on grey correlation and connection number coupling[J]. Journal of Catastrophology, 2019, 34(1): 1-7. (in Chinese)) |
| [27] |
ZOU Q, ZHOU J Z, ZHOU C, et al. Comprehensive flood risk assessment based on set pair analysis-variable fuzzy sets model and fuzzy AHP[J]. Stochastic Environmental Research and Risk Assessment, 2013, 27(2): 525-546. |
| [28] |
程乾生. 属性识别理论模型及其应用[J]. 北京大学学报(自然科学版), 1997, 33(1): 12-20. ( CHENG Qiansheng. Attribute recognition theoretical model with application[J]. Acta Scientiarum Naturalium Universitatis Pekinensis, 1997, 33(1): 12-20. (in Chinese)) |
2. Water Resources and Environmental Systems Engineering Institute, Hefei University of Technology, Hefei 230009, China
 2019
2019 
