2. 浙江省水利河口研究院,浙江 杭州 310007;
3. 杭州市河道管理总站,浙江 杭州 310014
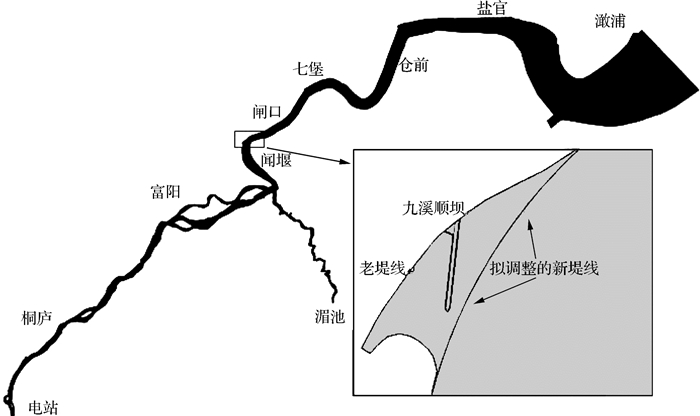
杭州城西地区地势低洼,上承西部山洪,下受平原河网高水位顶托,北排至太湖路径较长,历来是杭州城区防洪排涝问题较为突出的区域。为解决城西防洪排涝问题,杭州市拟建设城西南排通道工程,新建一条长约11 km、洞径约11 m的深埋排水隧洞,利用闲林湿地、五常湿地和西溪湿地将城西涝水汇流后直接南排入钱塘江,新增一条杭嘉湖平原直排钱塘江的排涝通道,同时兼顾杭州之江地区和西湖景区九溪十八涧的防洪御潮(图 1)。

|
图 1 城西南排通道工程示意图 Fig.1 Sketch map of Chengxi drainage channel project |
城西南排通道工程出口需布置大(1)型泵站、调压池等水工建筑物,占地规模较大。经论证,将现有钱塘江九溪弯道堤线适当外移,可满足出口水工建筑物布置的空间需求。九溪涌潮汹涌,大潮期潮水翻越至之江路,影响行人和车辆安全。堤线外移在满足工程功能要求的同时也减小了涌潮危害,但九溪涌潮是知名的观潮点,因此在堤线外移时必须对堤线方案进行优化,实现涌潮就近重塑。
由于钱塘江涌潮独特性,国内外学者也越来越关注钱塘江涌潮,针对涌潮数值计算、涉水建筑物对涌潮影响等方面已有不少的研究成果[1-5],但真正探讨钱塘江涌潮重塑的并不多见。本文建立涌潮数学模型,模拟堤线外移工程实施前后的流场及涌潮传播特性,从构筑物近区涌潮高度、涌高明显的岸线长度和涌高明显的区域面积等3个指标综合评判涌潮效果;利用物理模型试验,模拟涌潮的形成与传播过程,分析比较堤线外移工程实施后涌潮传播过程的壅高、越堤等变化情况,进一步验证涌潮效果。
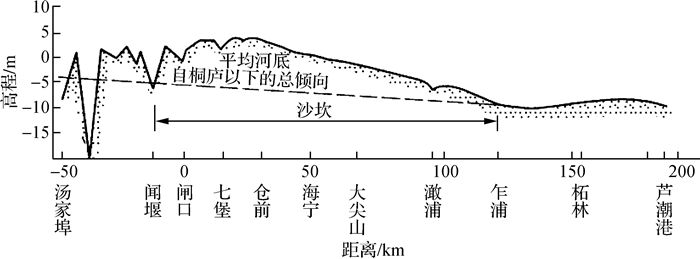
1 河段涌潮特征涌潮是钱塘江河口特殊的江道条件(纵向庞大的沙坎+喇叭形平面形态)下产生的水力学现象[6]。钱塘江涌潮的最大行进流速可达4~7 m/s,同一地点水位涨速可达1 m/s。因此涌潮既壮观,又具有很强的破坏性。从空间上看,涌潮形成于澉浦至大尖山一带,上溯过程中由于江道束窄,河床抬升,先是逐渐增强,至八堡—大缺口一带最大(图 2);之后由于涌潮传播中能量渐渐耗散,强度渐弱。强潮时潮头仍可上溯到闻堰以上,全程约90 km。从时间上看,涌潮多集中在每年的7—9月。当秋季大潮来临时,若前期水量充沛、汛期河床冲刷幅度大, 涌潮就会壮观。此时,九溪岸段则由于急弯和珊瑚沙水库围堤与下游堤防围成的局部喇叭形的平面形态共同作用,也能形成较为壮观的回头潮。
|
图 2 钱塘江河口河床纵剖面 Fig.2 Sandbed vertical profiles of Qiantang Estuary |
非恒定二维浅水流动方程守恒形式为
| $ \frac{\partial E}{\partial t}+\frac{\partial F}{\partial x}+\frac{\partial G}{\partial y}=S $ | (1) |
式中:
计算域采用任意三角形剖分,并采用网格中心格式,即将物理量定义在三角形形心,控制体即为单元本身。设Ωi为第i个三角形单元域,Гi为其边界,对式(1)应用有限体积法离散,并利用格林公式,则有:
| $ {A_i}\frac{{\partial E}}{{\partial t}} + \oint_\mathit{\Gamma } {(F\cos \theta + G\sin \theta )} {\rm{d}}l = \iint\limits_{{\mathit{\Omega }_i}} {{S_i}{\rm{d}}x{\rm{d}}y} $ | (2) |
式中:Ai为三角形单元Ωi的面积;(cosθ, sinθ)为Г外法向单位向量;dl为线积分微元。对式(2)时间导数采用前差,记Fn=Fcosθ+Gsinθ,即得基本数值解为:
| $ E_{i}^{n+1}=E_{i}^{n}-\frac{\Delta t}{A_{i}} \sum\limits_{j=1}^{3} F_{n j} l_{j}+\frac{\Delta t}{A_{i}} \iint\limits_{{\mathit{\Omega }_i}} S_{0 i} \mathrm{d} x \mathrm{d} y+\Delta t S_{\mathrm{f}i} $ | (3) |
式中:Δt为时间步长;下标j表示i单元第j边;lj为三角形边长;上标n为时间步;S0i为底坡源项;Sfi为阻力项。
求解式(3)的核心是法向数值通量的计算,本文采用KFVS(kinetic flux vector splitting)格式计算法向数值通量[7]。求解守恒型非平底浅水流动方程时,需对底坡源项作特殊的处理,以使方程左端的压力项与方程右端的底坡源项在每个单元内“和谐”,上述模型的静水和斜激波等典型算例检验见文献[7]。
2.2 数值模型验证本次数学模型研究范围上游边界选在富春江电站,下边界选在澉浦,结合涌潮特征计算需要,对闻家堰至七堡河段网格进行局部加密处理,最小网格尺度2 m。模型计算范围及网格布置如图 3所示。验证采用2018年6月实测1:1 000水下地形图,水文验证为2018年6月实测资料,潮位站有闸口、闻堰、富阳和九溪共4个,流速测点有5个。
|
图 3 涌潮数值计算范围 Fig.3 Numerical calculation range of tidal bore of Qiantang River |
计算模拟了钱塘江涌潮形成、发展及其衰减的过程,验证结果为:高潮位最大误差为0.37 m,低潮位最大误差0.10 m,各测点流速过程验证吻合较好,特别是各站点涨急流速、落急流速均能捕捉到。验证结果较为理想,可信度高,说明数学模型的各项参数取值合理,可用于城西南排通道工程钱塘江九溪岸段优化方案的计算分析[8]。
2.3 优化方案比较 2.3.1 计算条件及工况组合分析九溪岸段优化方案对钱塘江沿程各观潮点涌潮特征的影响,计算上游流量边界选择富春江电站多年平均径流流量,下游潮位边界选择典型秋季大潮过程,模型地形选择最新实测地形资料。
根据前期研究,影响钱塘江涌潮强弱的重要因素可归纳为潮汐、山水和江道地形等因素。对江道地形,计算水文条件选用钱塘江河口治理基本到位后的、江道容积偏大的年份,取当年潮差保证率接近1%(2.60 m)和20%大潮(1.77 m,本次水文测验期间实测大潮接近该值)。设计3种优化方案,分别为:方案1,将沿山河新闸紧贴珊瑚沙水库并往岸边调整,闸泵轴线平行布置; 方案2, 在九溪挡潮闸下游的三角区域内形成人工的喇叭口状岸线形态; 方案3,将沿山河新闸尽量往之江路一侧靠近,最大限度让出涌潮发展壮大通道。由此,计算组次包括工程实施前及3个优化方案等4种工况,组合前述两种水文条件,共为8组次。
2.3.2 涌潮重塑效果评判指标为综合评价涌潮的观赏性,将涌潮观赏性分解为构筑物近区涌潮高度、涌高明显的岸线长度和涌高明显的区域面积等3个指标。将近区涌潮高度指标权重设为0.4,岸线长度和区域面积权重均设为0.3,假定现状涌潮综合系数为1.0。各方案综合系数=方案实施后的各项指标值/现状的对应指标值×指标权重的合计值。需要说明的是,由于平面二维涌潮模型的局限性,目前尚无法模拟涌潮撞击建筑物后贴壁有限量水体冲天而起形成水花的这一过程,本文数值计算中的涌高主要是指近岸区大部分水体的平均涌潮涌高幅度。潮水撞击建筑物后的冲天潮效果通过物理模型进一步验证。
2.3.3 数值计算成果计算结果表明,涌高明显的主要有3个区域:沿山河老闸前、顺坝与海塘交叉口内侧和外侧。顺坝外侧、靠近江道主槽侧涌潮高度一般在0.7~0.8 m,沿山河老闸前沿涌高1.5 m。方案1实施后在新堤线外侧涌潮高度一般在0.7~0.8 m,沿山河新闸和九溪新闸由于局部内凹,对涌潮有集聚发展作用,涌高幅度上升至0.9 m左右。方案2也有类似规律,在九溪挡潮闸下游三角区区域内形成人工的喇叭口状岸线形态,涌潮在此集聚发展,近岸侧涌高1.5 m,效果最好。方案3在沿山河新闸内涌潮聚集效果也较为明显,近岸侧涌高1.1 m。限于篇幅,文中绘出了涌潮重塑效果最好的方案2实施前后的涌潮高度平面分布(图 4)。20%潮差保证率下工程涌潮重塑特征类似,不再赘述[8]。

|
图 4 方案2实施前后的涌潮高度平面分布(1%潮差保证率) Fig.4 Horizontal distribution of tidal bore surge height before & after the second optimization scheme while cumulated frequency of tidal range is 1% |
为了更全面反映各优化方案在涌潮强度、形态及观赏性的特点,分别采用1%和20%潮差保证率条件下岸段前沿明显区别于相邻区域的0.9和0.7 m涌高值,分别统计分析各组次中曾出现大于相应涌高值的岸线长度和面积见表 1。
| 表 1 各方案涌潮重塑计算成果 Tab.1 Calculation results of rebuilding tidal bore |
与现状相比,方案1中的涌潮高度减小明显,涌高明显的岸线长度也最小,涌浪明显的区域面积也是最小;方案2涌潮高度与方案前接近,掀起涌浪幅度明显的岸线长度和涌高明显的区域面积也为方案前的1/3左右;方案3与方案2结果较为一致,涌潮高度略小于方案2,但掀起涌浪幅度明显的岸线长度和涌高明显的区域面积稍大一些。
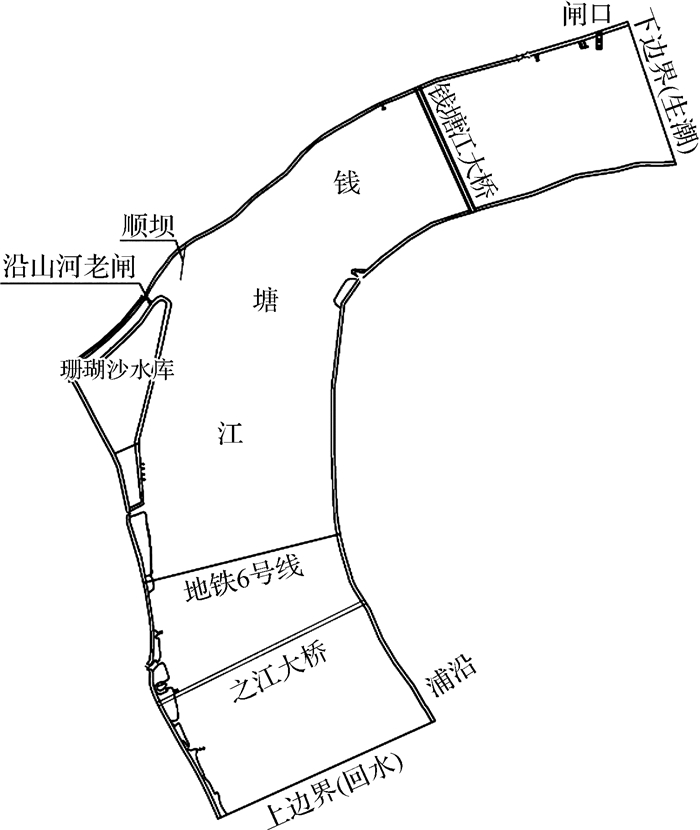
3 涌潮物理模型试验涌潮物理模型的上游边界布置取在杭州之江大桥附近,下游边界定在闸口断面附近(见图 5),模型平面比尺λL=150,垂直比尺为λH=50,模型控制系统采用先进的多台水泵变频调速、多口门闭环水位控制系统生潮。
|
图 5 涌潮物理模型布置 Fig.5 Layout of tidal bore physical model |
涌潮物理模型的涌潮水流条件主要是控制潮前低潮位及涌潮高度。因工程河段缺少涌潮实测资料,根据浙江省水利河口研究院对七堡、钱江二桥涌潮分析成果推算工程岸段涌潮高度大致为涨潮潮差的70%,据此,涌潮模型试验分别采用1.4,2.0及2.5 m的涌潮高度作为常见、3年一遇以及20年一遇的涌潮水流条件。
分析工程岸段下游闸口站自1998年以来低潮位与涨潮潮差的关系,钱塘江大潮汛期间涨潮潮差在2.0 m以上时的低潮位在2.8~4.4 m,本次模型试验中取该低潮位值。试验地形采用2018年6月实测地形。
3.1 现状模型试验结果现状条件下主要测试壅高及翻越至之江路水量。从试验中观测,在低潮位3.6 m、潮高1.4 m条件下,涌潮推进到沿山河排涝闸时水位壅高,有浪花溅到闸下游之江路海塘挡浪墙,但基本没有整体越堤水体,当涌潮高度增加到2.1 m时,闸前壅高增加,试验组次测到的最大壅高高程为13.5 m,回头潮水体越上之江路水量约200 m3。当涌潮高度增加到2.5 m时,试验测到的最大壅高高程为13.5 m,越上之江路的水量达到900 m3,模型中也测试极端大潮(低潮位3.9 m、潮高3.0 m)条件下,越上之江路的水量达到3 000 m3。
此外,涌潮推进到珊瑚沙水闸过程中,涌高受喇叭口地形的影响,有所抬升,遇闸反射后的壅高高程则更高。
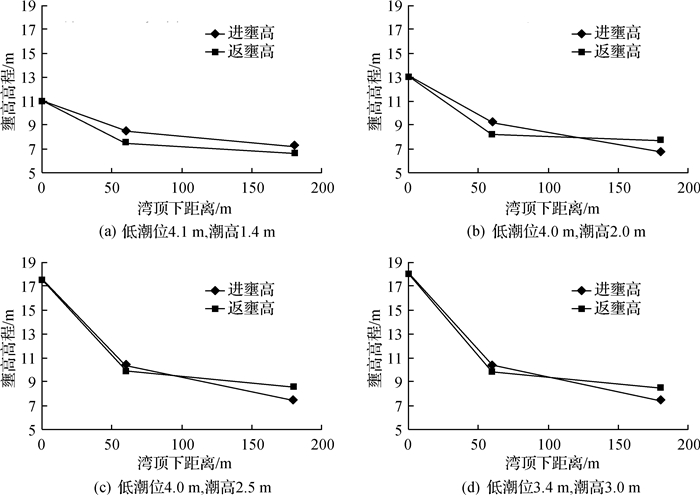
3.2 各优化方案模型试验结果从方案1试验中观测, 当涌潮行进到工程区外江侧时,涨潮侧向分流进入闸下,潮波前峰遇闸前后引起闸下水域一定程度的水位壅高,较大涌潮条件下,新闸上下局部区域有少量浪花水体越堤,珊瑚沙水库围堤外缘,因受涌潮直接顶冲,水体翻越珊瑚沙水库围堤(见图 6)。
|
图 6 喇叭形湾顶下沿程壅高变化试验成果 Fig.6 Physical model experiments' results of the change of run up height at the trumpet vault |
从方案2试验中观测,当下游涌潮推进到喇叭口处时,该喇叭形区域的涌潮强度迅速增加,水位进一步壅高,当涌潮高度1.4 m时,水体就翻越湾顶位置至新围堤(围堤高程9.3 m),之江路外侧的围堤则无水体越浪。当涌潮高度2.0 m时,喇叭形湾顶处越堤水量更多,有浪花溅到之江路,但没有明显的越堤水体。当涌潮强度达到2.5 m时,湾顶处的越堤水量更多,之江路仍然没有水体翻越。试验极端大潮(超高3.0 m)条件下,水体大量越过之江路外侧的新围堤,越堤水量从之江防洪堤与新围堤之间的区域流走。
从方案3试验中观测,在低潮位4.0 m、潮高1.4 m条件下,涌潮推进到新闸位置时,有浪花溅到闸上下的堤防上,越堤水量非常小。当涌潮高度增加到2.1 m时,闸前壅高增加,试验测到的最大壅高高程达到14.5 m,但越堤水量仍然较少。当涌潮高度增加到2.5 m时,试验测到的最大壅高高程为16.0 m,有一定量的水体翻越近闸上下围堤。
3.3 方案比较涌潮推进遇到丁坝、码头、水闸、急弯等处引起碰撞壅高,各方案试验条件下闸前(方案2为喇叭形弯顶)测试到的最大壅高见表 2。现状条件下,涌潮碰到沿山河老闸后反射,水位进一步壅高翻越之江防洪堤,低潮位4.0 m、潮高2.1 m条件下越堤水量约10 m3;方案1基本没有越堤;方案2的越堤水量超过现状工况;方案3的越堤水量与现状方案相当,越堤位置主要在新闸及周边。
| 表 2 闸前(弯顶)最大壅高比较(低潮位4.0 m) Tab.2 Comparison of maximum run up height before the sluice or the trumpet vault while the low tidal level is four meters |
方案1和3为沿新围堤外侧的涌潮侧向分流进入沿山河新闸和九溪挡潮闸下通道,涌潮强度与喇叭口外形和闸下通道的长度有关,方案1由于闸下没有一定长度的逐渐聚能空间,壅高及遇闸反射的高程在3个方案中最小;方案3闸下通道长度较长,至闸前壅高较大,大潮条件下越堤主要发生在新闸附近以及受涌潮直接顶冲的珊瑚沙水库围堤迎潮侧;方案2喇叭口的外形为涌潮直接顶冲区域,壅高高程和越堤水量在3个方案中最大。
4 结语(1) 为了满足城西南排通道工程出口功能布置要求,需将钱塘江九溪弯道珊瑚沙水库下游侧围堤至沿山河老闸岸段的堤线适当外移。堤线外移后虽减小了涌潮危害,但同时改变了九溪涌潮形成的物理条件。因此在堤线外移时需优化布局,创造条件实现涌潮就近重塑。
(2) 通过数值计算和物理模型试验验证,城西南排通道工程钱塘江九溪岸段优化实施后,九溪涌潮重塑具有可行性。其中,方案2兼具涌潮形成的喇叭口岸线形态、河床逐步抬升、涌潮正面迎击等多个有利因素,并且有利于相关排涝闸工程的布置与运行安全。
(3) 后续还应对方案2进行进一步细化,以控制涌浪使其不越过之江路,变潮害为潮景。
| [1] |
卢祥兴, 杨火其, 曾剑. 钱塘江下游建桥对涌潮景观影响的研究[J]. 海洋学研究, 2006, 24(1): 37-42. ( LU Xiangxing, YANG Huoqi, ZENG Jian. Influence of building the bridge in the downstream of the Qiantangjiang River on the tidal bore landscape[J]. Journal of Marine Sciences, 2006, 24(1): 37-42. DOI:10.3969/j.issn.1001-909X.2006.01.005 (in Chinese)) |
| [2] |
陈来华. 钱塘江河口大规模治江围涂后对涌潮高度的影响[J]. 水科学进展, 2007, 18(3): 385-389. ( CHEN Laihua. Effect of extensive regulation and reclamation of Qiangtang River on tidal bore height[J]. Advances in Water Science, 2007, 18(3): 385-389. DOI:10.3321/j.issn:1001-6791.2007.03.013 (in Chinese)) |
| [3] |
王灿星, 陈菊芳, 金晗辉, 等. 涌潮对钱塘江河道流场影响的三维数值模拟研究[J]. 水动力学研究与进展(A辑), 2012, 27(4): 367-375. ( WANG Canxing, CHEN Jufang, JIN Hanhui, et al. Three-dimensional numerical simulation of tidal bore of Qiantang River[J]. Chinese Journal of Hydrodynamics, 2012, 27(4): 367-375. (in Chinese)) |
| [4] |
LIU Huaxing, LI Jing, SHAO Songdong, et al. SPH modeling of tidal bore scenarios[J]. Natural Hazards, 2015, 75(2): 1247-1270. DOI:10.1007/s11069-014-1374-2 |
| [5] |
汪求顺, 潘存鸿. 不同湍流模式下钱塘江涌潮水流三维模拟[J]. 海洋工程, 2017, 35(1): 80-89. ( WANG Qiushun, PAN Cunhong. Three-dimensional simulation of tidal bore in the Qiantang River under different turbulence models[J]. The Ocean Engineering, 2017, 35(1): 80-89. (in Chinese)) |
| [6] |
韩曾萃, 戴泽蘅, 李光炳, 等. 钱塘江河口治理开发[M]. 北京: 中国水利水电出版社, 2003: 108-121. ( HAN Zengcui, DAI Zeheng, LI Guangbing, et al. Regulation and exploitation of Qiantang River[M]. Beijing: China Water Power Press, 2003: 108-121. (in Chinese))
|
| [7] |
潘存鸿, 徐昆. 三角形网格下求解二维浅水方程的KFVS格式[J]. 水利学报, 2006, 37(7): 858-864. ( PAN Cunhong, XU Kun. Kinetic flux vector splittingscheme for solving 2-D shallow water equations withtriangular mesh[J]. Journal of Hydraulic Engineering, 2006, 37(7): 858-864. DOI:10.3321/j.issn:0559-9350.2006.07.015 (in Chinese)) |
| [8] |
李志永, 吴辉, 黄姿菡, 等.杭州城西南排通道工程钱塘江九溪岸段优化分析专题研究(最终成果稿)[R].杭州: 浙江省水利河口研究院, 2018. (LI Zhiyong, WU Hui, HUANG Zihan, et al. Research on the optimization and analysis of Jiuxi reach of Qiantang River in the Chengxi drainage channel project of Hangzhou[R]. Hangzhou: Zhejiang Institute of Hydraulics and Estuary, 2018. (in Chinese))
|
2. Zhejiang Institute of Hydraulics and Estuary, Hangzhou 310007, China;
3. Hangzhou Estuary Channel Management Bureau, Hangzhou 310014, China
 2019
2019 