混凝土材料在使用过程中并不是单一应力状态且无法避免受到动荷载作用,如高层建筑和桥梁承受的风荷载和地震作用,那么如何评价混凝土结构是否安全,归根结底就是要研究混凝土材料在复杂应力状态下的动态性能与破坏准则。自Abrams[1]发现混凝土存在率敏感性以来,国内外学者先后对其进行了大量的试验研究和理论推导,但受限于多轴试验设备的复杂性[2],关于混凝土双轴动态试验研究还比较少[3-5]。郑金城等[6]对混凝土进行了不同应变速率和不同侧应力的双向受压试验,得到了混凝土抗压强度随加载速率增加而增加的结论;吴彬等[7]对混凝土进行了不同应变速率下双轴动态受压试验,认为双轴应力状态下力学参数比单轴应力状态均有所提高。关于应变速率对混凝土变形特性的影响,从目前研究成果来看,其规律并不明显,吕培印等[8-9]对边长为100 mm的混凝土立方体试件进行了单轴动态试验后得到了峰值应变基本不变的结论;彭刚等[10-12]通过对混凝土进行不同加载速率(10-5~10-2 s-1)试验,得到了混凝土弹性模量随加载速率的增大而增大的结论。纵观多年研究还发现,对复杂应力状态下大尺度混凝土动态力学特性的试验研究还不完善,需深入研究。
迄今为止,学者们已经提出了上百种破坏准则模型。有摩尔-库伦准则及其修正后的模型[13-14],这类破坏准则形式简单,但不能很好地描述复杂应力状态下混凝土的破坏[2];宋玉普等[15]提出的多轴应力状态下破坏准则,参数较多,表达式较为繁琐;另外,过镇海等[16]基于试验数据提出的一种满足拉压子午线和偏平面包络线的破坏准则,模拟效果好,但属于静态准则。总体而言,目前所提出的混凝土破坏准则仅在特定的应用范围内表现良好,对于复杂应力状态下的动态强度准则还需要进一步探究。
因此,本文利用真三轴试验机,对强度为C30,边长为300 mm的混凝土立方体进行不同侧压(0, 0.12fc, 0.24fc, 0.36fc, 0.48fc, fc为龄期60d的300mm×300 mm立方体试件单轴极限抗压强度平均值)和不同应变速率(10-5/s, 5×10-5/s, 10-4/s, 5×10-4/s, 10-3/s)下的动态压缩试验,得到应变速率和侧压对常态混凝土受压力学性能的影响,建立了混凝土动态双轴受压破坏准则,并基于其他学者的试验数据对该破坏准则进行了适用性验证分析。
1 试验概况 1.1 试件制备试验采用的混凝土试件根据《水工混凝土配合比设计规程》(DL/T 5330—2005)按C30强度进行配合比设计,其材料用量为:水175.0 kg/m3,水泥291.0 kg/m3,砂676.9 kg/m3,小石502.8 kg/m3,中石754.3 kg/m3。其中水泥采用P·O 42.5硅酸盐水泥,选用中砂,碎石粒径为5~40 mm,其中小石粒径5~20 mm,中石粒径20~40 mm,小石与中石的比例为4:6。试件采用300 mm的立方体,由钢模浇筑成型。搅拌时采用二次投料和先干拌后湿拌的方法,待试件浇筑完成,拆模后将试件放入标准养护室养护,90 d后将混凝土移至室外自然养护。
1.2 试验设备与过程(1) 试验设备:试验采用三峡大学的TAZW-10000型10 MN大型多功能液压伺服动静力三轴仪,有关设备详情见文献[10-12]。
(2) 试验过程:①装样及对中:将试件置于夹具内,放置于试验机下并严格对中;②变形计安装:安装变形计至试件周边并用仪器检验其传导正常;③预加载:利用移动和移动转换指令分别使试件竖向、侧向预加载至20 kN;④侧向加载:按拟定侧压力,采用负荷控制方式(2 000 N/s)加载至拟定大小(0, 0.12fc, 0.24fc, 0.36fc, 0.48fc);⑤竖向加载:利用移动转换命令中的变形控制方式进行操作,按预定加载速率(10-5/s, 5×10-5/s, 10-4/s, 5×10-4/s, 10-3/s)加载,直至试件破坏;⑥试验完成,保存荷载F和变形Δ的试验数据;⑦通过σ=F/A,ε=Δ/l得到应力和应变数据。
试验中,三轴仪控制加载速率为0.18 mm/min时对应的应变速率为10-5/s。
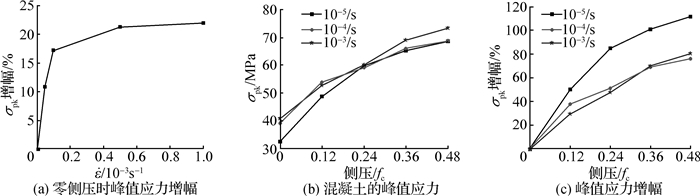
2 试验结果与分析 2.1 峰值应力试验得到混凝土在不同侧压和不同应变速率下的峰值应力见图 1。
|
图 1 侧压及应变速率对峰值应力的影响 Fig.1 Peak stress influence curves under lateral pressures and strain rates |
由图 1可见:①相同侧压下,混凝土峰值应力随应变速率的增大而增大;而相同应变速率加载时混凝土的峰值应力随着侧压的增大而增大。②当应变速率小于10-4/s时,混凝土的率效应很明显;当应变速率达到10-4/s时,混凝土抗压强度大大增加;当应变速率继续增大时,其对混凝土抗压强度的增益效果一般。③相同应变速率加载时,混凝土峰值应力随侧压的增大而增大,且应变速率越低,侧压对混凝土峰值应力的增益作用越明显。
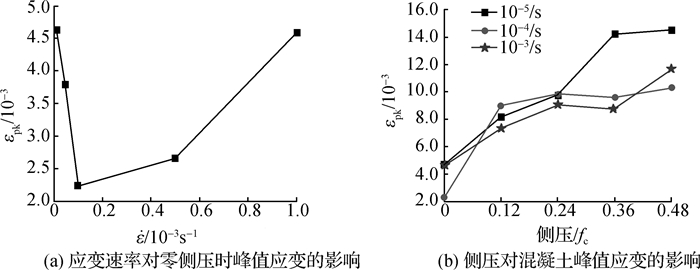
2.2 峰值应变试验得到混凝土在不同侧压和不同应变速率下的峰值应变如图 2所示,可见:①基于试验数据,得出应变速率在10-5/s~10-3 /s范围内时,混凝土峰值应变在2×10-3~5×10-3,虽然其变化范围数量级很小,且混凝土存在一定离散性,但仍然存在着先减后增规律。②应变速率相同时,峰值应变随侧压增大而增大;应变速率较低时,侧压对峰值应变的影响更明显,可见应变速率改变了混凝土对侧压的敏感性。
|
图 2 侧压及应变速率对峰值应变的影响 Fig.2 Peak strain influence curves under lateral pressures and strain rates |
弹性模量取峰值应力的35%~45%时的应力-应变全曲线割线斜率。试验得到混凝土在不同侧压和不同应变速率下弹性模量如图 3所示,可见:①随应变速率增大,混凝土弹性模量呈先增后减趋势。②由于混凝土材料本身力学特性的离散性较大,10-5/s~10-3/s的加载速率范围内,侧压对混凝土弹性模量的影响不明显。

|
图 3 侧压及应变速率对弹性模量的影响 Fig.3 Influence curves of concrete elastic modulus under lateral pressures and strain rates |
作为常用二维结构的Kupfer-Gerstle[17]准则在主应力空间上的破坏准则,经修正后被纳入欧洲模式规范[18];考虑应变速率对混凝土力学性能的影响,建立基于K-G准则的动态双轴受压破坏准则。对于混凝土双轴受压破坏准则,假定动态加载时曲线仍与静态加载时的曲线相似,那么K-G准则中的fc则需替换为某个应变速率下混凝土的动态单轴抗压强度fc, d,即:
| $ \sigma_{3} / f_{\mathrm{c}, \mathrm{d}}=\left[a+b\left(\sigma_{2} / f_{\mathrm{c}, \mathrm{d}}\right)\right] /\left(1+\sigma_{2} / f_{\mathrm{c}, \mathrm{d}}\right)^{2} $ | (1) |
式中:σ3为抗压强度;σ2为侧压强度;a和b为试验拟合参数。fc, d的确定基于本文不同应变速率单轴峰值应力数据,结合吕培印等[8-9]研究的线性表达式(2)与欧洲规范[18]中的非线性关系式(3)进行拟合。
| $ {f_{{\rm{c, d}}}}/{f_{\rm{c}}} = \alpha + \beta \ln \left( {{{\dot \varepsilon }_0}/{\varepsilon _0}} \right) $ | (2) |
| $ f_{\mathrm{c}, \mathrm{d}} / f_{\mathrm{c}}=\left\{\begin{array}{l}{\left(\dot{\varepsilon}_{0} / \varepsilon_{0}\right)^{1.026 \alpha}, \dot{\varepsilon} \leqslant 30 / \mathrm{s}} \\ {\beta \dot{\varepsilon}^{1 / 3}, \dot{\varepsilon}>30 / \mathrm{s}}\end{array}\right. $ | (3) |
式中:fc, d为混凝土动态抗压强度;
吕培印等[8-9]的研究中,取α=1.025,β=0.109 2,R2=0.918 2,欧洲规范中取α=0.047 63,R2=0.859 8。可以看出,吕培印等研究的线性表达式对本文数据拟合准确度更高,故选式(2)构建双轴动态破坏准则。其fc, d的表达式为fc, d=(1.025+0.047 43ln(
采用已构建的双轴动态破坏准则对10-5/s,10-4/s,10-3/s应变速率下的双轴压缩试验数据进行拟合,所得参数如表 1所示,参数a受应变速率的影响很小,仅在1上下波动,且变化幅度小于5%,不妨假设a=1;而参数b变化较大,遂将式(1)变为式(4);由表 1可以看出参数b的取值随着应变速率的增大而减小,近似地可以采用式(5)。式(5)通过表 1的数据拟合分析,得到b1=5.509,b2=-0.257 3,则最终的改进K-G准则表达式如式(6)所示。
| 表 1 混凝土动态双轴压破坏准则参数 Tab.1 Failure criterion parameters of concrete under dynamic biaxial compression |
| $ \sigma_{3} / f_{\mathrm{c}, \mathrm{d}}=\left[1+b\left(\sigma_{2} / f_{\mathrm{c}, \mathrm{d}}\right)\right] /\left(1+\sigma_{2} / f_{\mathrm{c}, \mathrm{d}}\right)^{2} $ | (4) |
| $ b=b_{1}+\exp \left(b_{2} \ln \dot{\varepsilon}\right) $ | (5) |
| $ {\sigma _3}/{f_{{\rm{c, d}}}} = \left[ {1 + \left( {{b_1} + \exp \left( {{b_2}\ln \dot \varepsilon } \right)} \right)\frac{{{\sigma _2}}}{{{f_{{\rm{c, d}}}}}}} \right]/{\left( {1 + {\sigma _2}/{f_{{\rm{c, d}}}}} \right)^2} $ | (6) |
基于式(4)和(6),模型分别对10-5/s, 10-4/s, 10-3/s应变速率下的双轴压缩试验数据进行拟合(见图 4)。由图 4可见:①应变速率大的曲线位于应变速率较小的曲线上方,充分说明了混凝土的率效应,并且应变速率越高,率效应越明显。②基于改进后的K-G准则所画曲线,通过计算,应变速率10-5/s, 10-4/s, 10-3/s时的样本点与破坏准则曲线之间的平均误差分别为1.21%, 1.99%, 2.69%,可见基于改进后K-G准则建立的动态双轴受压模型能较好地应用于本文。

|
图 4 两种K-G准则的动态双轴混凝土受压模型与样本点对比 Fig.4 Comparison between curves given by dynamic biaxial compression model and sample points based on two K-G criteria |
引用文献[19]中边长为100 mm的普通混凝土立方体试件进行不同应变速率和不同侧压的试验分析,所得数据见表 2。
根据侧压试验数据拟合得到单轴强度准则为:fc, d/fc=0.997 4+0.083 23ln(
| 表 3 基于改进K-G模型对应文献[19]数据的参数 Tab.3 Parameters of corresponding literature [19] data based on improved K-G model |
从表 3可见,采用改进K-G模型与试验数据的吻合度极高,并且参数b与加载速率之间的关系为:b=4.012+exp(-0.119 1ln
| $ \frac{\sigma_{3}}{f_{\mathrm{c}}}=\frac{0.9974+0.08323 \ln \left(\dot{\varepsilon} / \dot{\varepsilon}_{0}\right)+(4.012+\exp (-0.1191 \ln \dot{\varepsilon})) \sigma_{2} / f_{\mathrm{c}}}{\left(1+\frac{\sigma_{2}}{f_{\mathrm{c}}\left(0.9974+0.08323 \ln \left(\dot{\varepsilon} / \dot{\varepsilon}_{0}\right)\right)}\right)^{2}} $ | (7) |
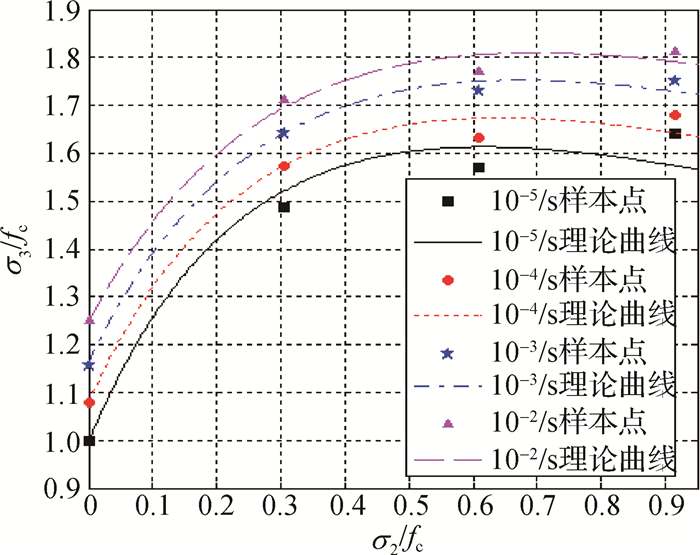
采用式(7)绘制的模型曲线与试验样本点间的对比如图 5所示。由图 5可得:10-5/s,10-4/s,10-3/s和10-2/s时理论曲线的平均误差分别为2.37%,1.19%,0.98%和1.05%,改进K-G模型能准确估算不同加载速率和侧压下的混凝土极限强度。
|
图 5 基于改进后K-G准则的动态双轴受压模型与文献[19]样本点对比 Fig.5 Comparison between curves given by dynamic biaxial compression model and literature[19] sample points based on improved K-G criterion |
(1) 本次研究主要针对地震作用引起的混凝土材料响应,选择10-5/s~10-3/s的加载速率进行试验,其研究更具真实性,并且300 mm立方体混凝土能对目前主流150 mm标准试件动态力学特性的研究成果进行补充。
(2) 应变速率越大,峰值应力也越大,并且当应变速率小于10-4/s时,混凝土的率效应很明显,应变速率继续增大,其对混凝土峰值应力的增益作用逐渐减弱。混凝土峰值应变随应变速率的增大呈先减后增趋势。弹性模量随应变速率的增大呈先增后减趋势。
(3) 侧压应力对混凝土峰值应力和峰值应变的影响显著,对弹性模量无明显影响。
(4) 基于K-G破坏准则,考虑动态特性,确定了一种改进的K-G破坏准则,该准则具有较强的适用性。
| [1] |
ABRAMS D A. Effect of rate of application of load on the compressive strength of concrete[J]. ASTM J, 1917, 17(34): 364-377. |
| [2] |
孟顺意.混凝土双轴动态试验研究[D].大连: 大连理工大学, 2010. (MENG Shunyi. Double axial dynamic test of concrete[D]. Dalian: Dalian University of Technology, 2010. (in Chinese)) http://cdmd.cnki.com.cn/Article/CDMD-10141-1011021621.htm
|
| [3] |
MATSTEIN D. Effect of straining rate on the compressive strength and elastic properties of concrete[J]. ACI J, 1953, 49(4): 729-744. |
| [4] |
SUN J S, MA L J, DOU Y M, et al. Effect of strain rate on the compressive mechanical properties of concrete[J]. Advanced Materials Research, 2012, 450-451: 244-247. DOI:10.4028/www.scientific.net/AMR.450-451.244 |
| [5] |
TEDESCO J W, POWELL J C, ROSS C A, et al. A strain-rate-dependent concrete material model for ADINA[J]. Computer and Structures, 1997, 64(5/6): 1053-1067. |
| [6] |
郑金城, 徐超, 彭刚, 等. 预静态加载后的混凝土动态受压特性试验[J]. 实验力学, 2013, 28(3): 352-359. ( ZHENG Jincheng, XU Chao, PENG Gang, et al. Experimental study on dynamic compressive behaviors of concrete due to monotonic loading history[J]. Journal of Experimental Mechanics, 2013, 28(3): 352-359. (in Chinese)) |
| [7] |
吴彬, 彭刚, 周寒清. 双轴受压下混凝土动态力学特性试验研究[J]. 水电能源科学, 2013, 31(5): 100-102, 148. ( WU Bin, PENG Gang, ZHOU Hanqing. Experimental study on dynamic mechanical properties of concrete under biaxial compression[J]. Water Resources and Power, 2013, 31(5): 100-102, 148. (in Chinese)) |
| [8] |
吕培印, 宋玉普. 混凝土动态压缩试验及其本构模型[J]. 海洋工程, 2002, 20(2): 43-48. ( LÜ Peiyin, SONG Yupu. Dynamic compression test of concrete and its constitutive model[J]. The Ocean Engineering, 2002, 20(2): 43-48. DOI:10.3969/j.issn.1005-9865.2002.02.008 (in Chinese)) |
| [9] |
闫东明, 林皋. 混凝土单轴动态压缩特性试验研究[J]. 水科学与工程技术, 2005(6): 8-10. ( YAN Dongming, LIN Gao. Experimental study on uniaxial dynamic compression properties of concrete[J]. Water Science and Engineering Technology, 2005(6): 8-10. DOI:10.3969/j.issn.1672-9900.2005.06.004 (in Chinese)) |
| [10] |
彭刚, 王乾峰, 梁春华. 有压孔隙水环境中的混凝土动态抗压性能研究[J]. 土木工程学报, 2015, 48(1): 11-18. ( PENG Gang, WANG Qianfeng, LIANG Chunhua. Study on dynamic compressive properties of concrete under pore water pressure environment[J]. China Civil Engineering Journal, 2015, 48(1): 11-18. (in Chinese)) |
| [11] |
肖洋, 彭刚, 王乾峰, 等. 考虑率效应的混凝土压剪强度及破坏准则试验研究[J]. 水利水运工程学报, 2018(4): 46-53. ( XIAO Yang, PENG Gang, WANG Qianfeng, et al. Experimental studies on compressive shear strength and failure criterion of concrete considering rate effect[J]. Hydro-Science and Engineering, 2018(4): 46-53. (in Chinese)) |
| [12] |
XIAO Yang, PENG Gang, HUANG Chao, et al. Damage evolution study of concrete under joint action of compression and shear[J]. Hydro-Science and Engineering, 2018(2): 112-119. |
| [13] |
王哲. 混凝土含损伤的摩尔-库伦强度模型试验研究[J]. 北京交通大学学报, 2013, 37(4): 84-88. ( WANG Zhe. Experimental study on Mohr-Coulomb model with damage for concrete[J]. Journal of Beijing Jiaotong University, 2013, 37(4): 84-88. (in Chinese)) |
| [14] |
高金良, 梅甫良. 基于莫尔强度理论的钢管混凝土轴心受压短柱承载力计算[J]. 四川建筑科学研究, 2007, 33(5): 126-129. ( GAO Jinliang, MEI Fuliang. Strength calculation of concrete filled steel tubular short columns under axial compression based on Mohr's strength theory[J]. Sichuan Building Science, 2007, 33(5): 126-129. DOI:10.3969/j.issn.1008-1933.2007.05.035 (in Chinese)) |
| [15] |
宋玉普, 赵国藩, 彭放, 等. 多轴应力下多种混凝土材料的通用破坏准则[J]. 土木工程学报, 1996, 29(1): 25-32. ( SONG Yupu, ZHAO Guofan, PENG Fang, et al. General failure criteria for different concrete materials under multiaxial stresses[J]. China Civil Engineering Journal, 1996, 29(1): 25-32. (in Chinese)) |
| [16] |
过镇海, 王传志. 多轴应力下混凝土的强度和破坏准则研究[J]. 土木工程学报, 1991, 24(3): 1-14. ( GUO Zhenhai, WANG Chuanzhi. Investigation of strength and failure criterion of concrete under multi-axial stresses[J]. China Civil Engineering Journal, 1991, 24(3): 1-14. (in Chinese)) |
| [17] |
KUPFER H, GERSTLE K H. Behavior of concrete under biaxial stresses[J]. Journal of Engineering Mechanics, 1973, 99(4): 853-866. |
| [18] |
Comite Euro-International du Beton. Bulletin d'information NO. 213/214, CEB-FIP model code 1990: Concrete structures[S]. Lausanne, Switzerland: Comite Euro-International du Beton, 1993.
|
| [19] |
闫东明, 林皋, 刘钧玉, 等. 定侧压下混凝土的双轴动态抗压强度及破坏模式[J]. 水利学报, 2006, 37(2): 200-204. ( YAN Dongming, LIN Gao, LIU Junyu, et al. Dynamic biaxial compressive strength and fracture pattern of concrete with constant confining pressure[J]. Journal of Hydraulic Engineering, 2006, 37(2): 200-204. DOI:10.3321/j.issn:0559-9350.2006.02.012 (in Chinese)) |
 2019
2019 

