2. 东南大学土木工程学院,江苏 南京 210096
桩基础在岩土工程中应用非常广泛,设计时基本采用确定性方法[1-2],而岩土体是自然界的产物,具有很强的空间变异性。因此,研究土体性质的空间变异性对桩基础的影响很有必要。
考虑土体性质空间变异性对桩基础的影响,首先需要采用随机场理论模拟出土体参数变异性,然后再应用到桩基础的设计计算过程中。常见的生成随机场方法有谱分解法[3]、K-L级数展开法[4-5]、局部平均法[6-7]、中心点法[8]等。Wu等[9]在已有谱分解法基础上,提出了基于相干函数矩阵特征正交分解法,这种方法的误差远小于其他谱表示法,且极大提升了计算效率,后续计算过程中将采用该方法。
考虑岩土体空间变异性的土工结构分析已有不少研究成果,包括边坡稳定性[10-12]、浅基础[13-14]和深基础[15-20]的承载性能等。桩基础方面,刘润等[16]对渤海海域中海工结构物桩基础的稳定性进行了可靠度分析,指出在渤海海域中依据API标准进行设计是安全可靠的。赵春风等[17]结合随机场理论和误差传递原理研究了利用CPT确定桩基竖向抗压承载力的可靠度指标及其统计特性。Haldar等[18]应用随机场理论对桩基础水平承载力进行了可靠度分析。张子富等[19]对组合荷载作用下特高压输电线路杆塔桩基础的承载力进行了可靠度分析,指出可靠度指标随土力学参数指标变异系数增大而减小。Teixeira等[20]应用一阶可靠度法和蒙特卡罗法(Monte Carlo)对竖向受荷桩的可靠度开展了敏感性分析, 洪昌华等[21]对碎石桩复合地基承载力进行了可靠度分析。
从上述分析可知,已有研究更多的是针对某个具体区域土性参数的变异性,分析桩基础可靠度,或是针对某个具体受荷特性的桩基础进行可靠度分析,还未见土体空间变异性影响竖向受荷桩的规律性研究成果。因此,本文采用文献[9]中的随机场模拟方法,通过ABAQUS软件分析桩基础竖向承载力随土性参数空间变异性的变化规律,以期加深对桩基受土体空间变异性影响的认识。
1 模型建立与工况设定 1.1 模型建立采用ABAQUS软件进行二维模拟。模型中假定地基土为黏土,土体密度为1.3 g/cm3,弹性模量为30 MPa,泊松比为0.45,不排水强度为30 kPa。桩身为钢筋混凝土,密度为2.5 g/cm3,弹性模量为30 GPa,泊松比为0.2,桩长16 m,直径0.8 m。土体采用Mohr-Coulomb屈服准则的理想弹塑性模型,桩体采用线弹性本构模型。
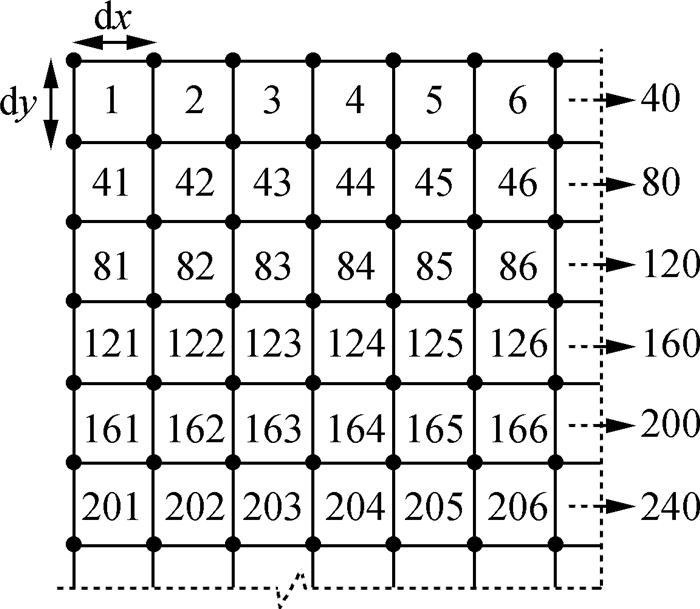
模型宽20 m,高24 m,土体网格按0.5 m×0.5 m划分,并按图 1所示编号;桩体网格按0.5 m×0.4 m划分,整个模型网格数量为48×40=1 920个,其中土体单元1 856个,桩体单元64个。模型左右两侧设为无水平位移,底部完全固定。桩体与地基土之间接触属性切向类型为“罚”,法向类型为“硬接触”。
|
图 1 有限元网格划分 Fig.1 Diagram of finite element meshing |
随机场模拟中,桩体材料属性以及土体弹性模量和泊松比等参数与确定性模拟中相同,土体不排水抗剪强度由随机场模拟得到。具体方法是,对土体模型进行网格划分后,对照划定的有限元网格,应用文献[9]中的方法模拟生成对应每个位置的土性参数,映射到有限元模型中,赋予每个单元不同的土体材料属性,以体现土体参数的空间变异性。
1.2 工况设置本次数值分析分为确定性分析和随机场分析两种,确定性分析即不考虑土参数的随机特性,土体是均匀且各向同性的。为了研究土体强度参数空间变化对桩基竖向承载力的影响,分别考虑了水平向相关距离8和16 m,竖向相关距离4和8 m,变异系数根据不同工况设置了3~5组,范围为10%~50%。具体工况设置如表 1所示(例:X8Y4Cov01表示水平相关距离8 m,竖向相关距离4 m,变异系数为10%)。在相同的变异系数和相关距离下,应用蒙特卡罗法的思想进行1 000次模拟,对应1 000个模型。模拟过程中,虽然土的不排水强度的基本统计特征值保持不变,但每次模拟中参数的空间分布却不相同,所以模拟得到的结果也不相同,用以呈现随机场导致土性参数及相应运算结果的不确定性。
| 表 1 工况设置及编号 Tab.1 Test programs and numbers |
关于桩基础承载力的确定,对于陡降型荷载-位移曲线,取发生明显陡降起始点对应的荷载值为桩基础的竖向承载力;对于缓变型荷载-位移曲线,取位移达到40 mm时对应的荷载为桩基础竖向承载力。
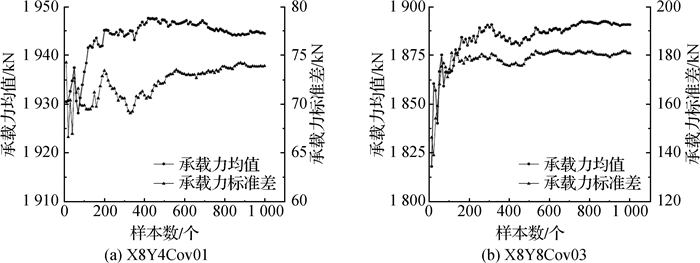
2.1 样本容量分析图 2为样本容量对桩基竖向承载力均值和标准差的影响曲线(以工况X8Y4Cov01和X8Y8Cov03为例),图中每个数据点分别表示1个样本中的模型数量与对应的单桩竖向承载力均值和标准差。从图 2中可以看出,随着样本数增大,桩基承载力均值和标准差均趋于稳定,浮动范围逐渐减小,说明选择的1 000个样本数满足样本大小的要求。
|
图 2 样本容量对桩基竖向承载力均值及标准差的影响曲线 Fig.2 Curves of influences of sample capacity on mean value and standard deviation of vertical bearing capacity of pile foundation |
图 3是确定性和随机场模拟得到的竖向荷载作用下桩基荷载-位移曲线(以工况X8Y8为例)。每个工况中,由于曲线太多,所以未将随机场模拟得到的1 000条曲线全部画入图中,而是从1 000条荷载-位移曲线中随机选取100条曲线绘入同一张图中。图中灰色曲线代表这100条随机选出的曲线,红色曲线代表 1 000条曲线的中值曲线(桩基承载力大小排在1 000个结果中的第500位),蓝色曲线为确定性分析得到的曲线。从图 3可见,任一工况下,大部分随机场分析得到的桩基荷载-位移曲线位于确定性分析曲线下方,即在相同大小荷载的条件下,随机场模型中的大部分桩基会产生更大的位移。

|
图 3 竖向荷载作用下桩基础荷载-位移曲线 Fig.3 Load-displacement curves of pile foundation under vertical loading |
对比图 3中5张不同变异系数的荷载-位移曲线可以看出,随着土体强度参数变异系数的增大,随机场分析得到的桩基荷载-位移曲线越来越分散,即桩基承载力差异越来越大。当变异系数为10%时,桩基荷载-位移曲线差异较小,集中在一个较小范围;当变异系数增大为50%时,桩基荷载-位移曲线很分散,差异很大。此外,随着土体变异系数增大,随机场分析得到的中值曲线代表的桩基承载力逐渐降低,以图 3中X8Y8工况为例,变异系数为10%, 30%和50%对应的桩基承载力中值分别为1 944.1,1 886.0和1 826.7 kN,与确定性分析得到桩基承载力2 152.3 kN差距越来越大。
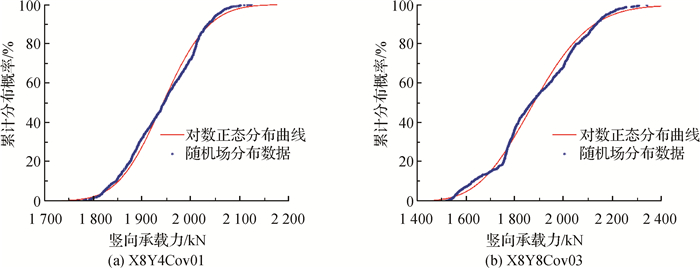
对随机场分析得到的任一工况1 000个计算结果进行统计分析,以小于某承载力的模型个数占总数的百分比作为纵坐标,以桩基竖向承载力作为横坐标,绘出分布概率图,如图 4所示(以X8Y4Cov01和X8Y8Cov03为例)。将样本数据取对数,把新的样本均值和样本方差作为均值和方差,做出对数正态分布的累计分布函数曲线,如图 3中红色曲线所示。观察图 4可以发现,桩基承载力累计分布曲线与对数正态分布曲线十分吻合,说明对数正态分布曲线可以很好地描述承载力数据的分布规律。因此,当样本容量足够大时,可由样本推测总体,这样就可以根据对数正态分布曲线获取任一荷载下桩基础的失效概率。
|
图 4 桩基础承载力累计分布曲线 Fig.4 Cumulative distribution curves of vertical bearing capacity of pile foundation |
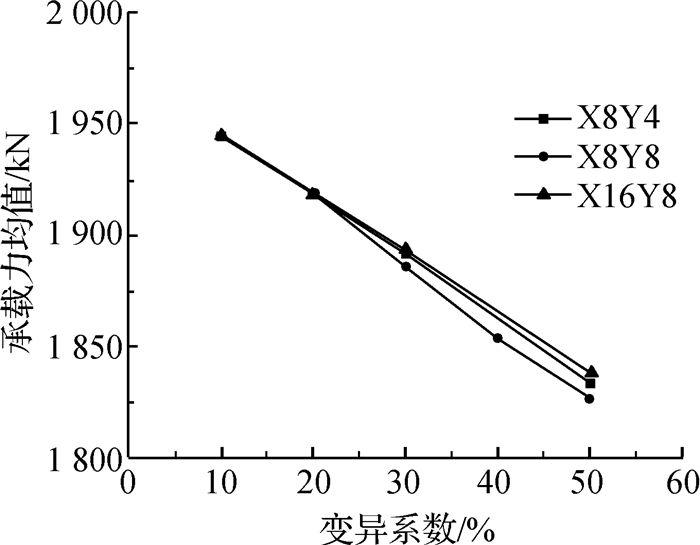
图 5和6分别是考虑土体空间变异性模拟得到桩基竖向承载力的平均值和标准差随土体不排水抗剪强度变异系数的变化曲线。
|
图 5 承载力均值与土体强度参数变异系数关系曲线 Fig.5 Relationships between mean value of bearing capacity and variability coefficient of soil strength parameters |
|
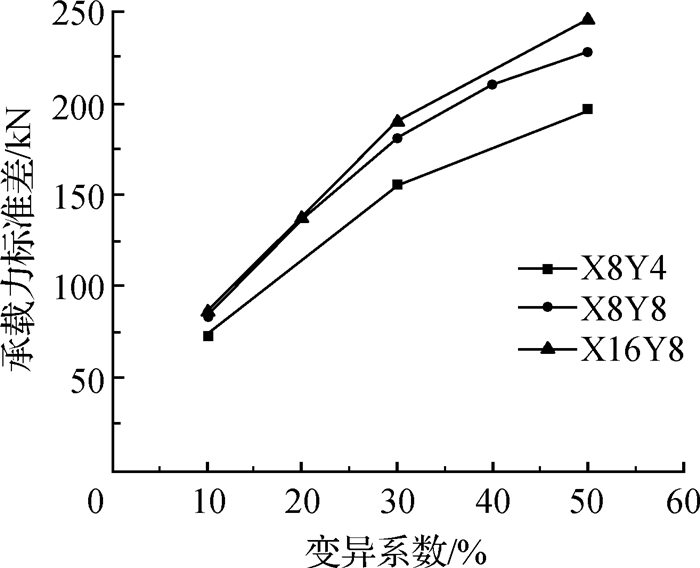
图 6 承载力标准差与土体强度参数变异系数关系曲线 Fig.6 Relationships between standard deviation of bearing capacity and variability coefficient of soil strength parameters |
观察图 5和6可以发现,在相同的相关距离条件下,桩基承载力均值随着变异系数的增大而呈现出近乎线性降低的趋势,并且承载力标准差随着变异系数的增大而增大,但变异系数从10%增大到50%的过程中,标准差的增长速率逐渐放缓。从图 6中还可以看出,在纵坐标维度上,3条曲线有高低之分,曲线X8Y4最低,曲线X16Y8最高,说明桩基承载力标准差随土体不排水强度的相关距离增大而增大。图 5中的3条曲线也存在一定差异,在相同的变异系数条件下,桩基承载力均值的大小关系为X16Y8>X8Y4>X8Y8,说明桩基承载力的均值与相关距离间的关系不是单调的,总体而言这3条曲线非常接近,说明相关距离对竖向承载力影响相对较小。
3 结语以强度参数表征土体性质的空间变异性,应用已有方法建立土体随机场模型,通过数值模拟分析了竖向荷载作用下考虑土性空间变异性的桩基础承载性能的变化规律,得到了如下结论:
(1) 考虑土性空间变异性后,桩基承载力的中值都小于确定性分析得到的桩基承载力。对于桩端非完全固定的桩基,随着土体强度参数变异系数的增大,桩基承载力中值基本呈线性减小趋势,但承载力标准差随之增大。实际工程中,需重点关注土体参数变异性大的工况。
(2) 桩基承载力标准差随土体强度参数相关距离的增大而增大,这会提高桩基承载力不确定性。
(3) 考虑土性强度参数空间变异性的桩基竖向承载力分布规律可用对数正态分布曲线来描述。当样本容量足够大时,可由样本推测总体,从而获取任一荷载下桩基础的失效概率。
| [1] |
JGJ 94—2008建筑桩基技术规范[S]. (JGJ 94—2008 Code for techniques of pile foundation work[S]. (in Chinese))
|
| [2] |
GB 50007—2011建筑地基基础设计规范[S]. (GB 50007—2011 Specification for foundation design of building foundation[S]. (in Chinese))
|
| [3] |
SHINOZUKA M, DEODATIS G. Simulation of multi-dimensional Gaussian stochastic fields by spectral representation[J]. Applied Mechanics Reviews, 1996, 49(1): 29-53. DOI:10.1115/1.3101883 |
| [4] |
MELINK T, KORELC J. Stability of Karhunen-Loève expansion for the simulation of Gaussian stochastic fields using Galerkin scheme[J]. Probabilistic Engineering Mechanics, 2014, 37: 7-15. DOI:10.1016/j.probengmech.2014.03.006 |
| [5] |
李典庆, 蒋水华, 周创兵, 等. 考虑参数空间变异性的边坡可靠度分析非侵入式随机有限元法[J]. 岩土工程学报, 2013, 35(8): 1413-1422. ( LI Dianqing, JIANG Shuihua, ZHOU Chuangbing, et al. Reliability analysis of slopes considering spatial variability of soil parameters using non-intrusive stochastic finite element method[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(8): 1413-1422. (in Chinese)) |
| [6] |
FENTON G A, GRIFFITHS D V. Three-dimensional probabilistic foundation settlement[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2005, 131(2): 232-239. DOI:10.1061/(ASCE)1090-0241(2005)131:2(232) |
| [7] |
苏成, 徐瑞, 范学明. 二维随机场离散的曲边单元局部平均法[J]. 华南理工大学学报(自然科学版), 2008, 36(3): 104-107, 120. ( SU Cheng, XU Rui, FAN Xueming. Local average method based on curved-side elements for discretization of 2D random fields[J]. Journal of South China University of Technology (Nature Science Edition), 2008, 36(3): 104-107, 120. DOI:10.3321/j.issn:1000-565X.2008.03.022 (in Chinese)) |
| [8] |
蒋水华, 李典庆, 周创兵, 等. 考虑自相关函数影响的边坡可靠度分析[J]. 岩土工程学报, 2014, 36(3): 508-518. ( JIANG Shuihua, LI Dianqing, ZHOU Chuangbing, et al. Slope reliability analysis considering effect of autocorrelation functions[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(3): 508-518. (in Chinese)) |
| [9] |
WU Y, GAO Y, LI D, et al. Study of the approximate approaches to the POD based spectral representation method[J]. Science China Technological Sciences, 2013, 56(4): 970-979. DOI:10.1007/s11431-013-5180-y |
| [10] |
GAO Y, ZHU D, ZHANG F, et al. Stability analysis of three-dimensional slopes under water drawdown conditions[J]. Canadian Geotechnical Journal, 2014, 51(11): 1355-1364. DOI:10.1139/cgj-2013-0448 |
| [11] |
李典庆, 祁小辉, 周创兵, 等. 考虑参数空间变异性的无限长边坡可靠度分析[J]. 岩土工程学报, 2013, 35(10): 1799-1806. ( LI Dianqing, QI Xiaohui, ZHOU Chuangbing, et al. Reliability analysis of infinite soil slopes considering spatial variability of soil parameters[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(10): 1799-1806. (in Chinese)) |
| [12] |
祁小辉, 李典庆, 曹子君, 等. 考虑地层变异的边坡稳定不确定性分析[J]. 岩土力学, 2017, 38(5): 1385-1396. ( QI Xiaohui, LI Dianqing, CAO Zijun, et al. Uncertainty analysis of slope stability considering geological uncertainty[J]. Rock and Soil Mechanics, 2017, 38(5): 1385-1396. (in Chinese)) |
| [13] |
CHO S E, PARK H C. Effect of spatial variability of cross-correlated soil properties on bearing capacity of strip footing[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2010, 34(1): 1-26. |
| [14] |
SIVAKUMAR BABU G L, SRIVASTAVA A, MURTHY D S N. Reliability analysis of the bearing capacity of a shallow foundation resting on cohesive soil[J]. Canadian Geotechnical Journal, 2006, 43(2): 217-223. DOI:10.1139/t05-099 |
| [15] |
LI L, LI J H, HUANG J S, et al. Bearing capacity of spudcan foundations in a spatially varying clayey seabed[J]. Ocean Engineering, 2017, 143: 97-105. DOI:10.1016/j.oceaneng.2017.05.026 |
| [16] |
刘润, 闫澍旺. 渤海湾地基土随机场特性及可靠度分析[J]. 岩土工程学报, 2004, 26(4): 464-467. ( LIU Run, YAN Shuwang. Random field model and reliability analysis of foundation soil in Bohai gulf[J]. Chinese Journal of Geotechnical Engineering, 2004, 26(4): 464-467. DOI:10.3321/j.issn:1000-4548.2004.04.007 (in Chinese)) |
| [17] |
赵春风, 徐超, 高大钊. 基于随机场模型的桩基竖向承载力可靠性分析[J]. 地下空间, 2004, 24(4): 449-452, 464. ( ZHAO Chunfeng, XU Chao, GAO Dazhao. Reliability analysis of vertical bearing capacity of pile based on random field theory[J]. Chinese Journal of Underground Space and Engineering, 2004, 24(4): 449-452, 464. DOI:10.3969/j.issn.1673-0836.2004.04.006 (in Chinese)) |
| [18] |
HALDAR S, BABU G L S. Effect of soil spatial variability on the response of laterally loaded pile in undrained clay[J]. Computers and Geotechnics, 2008, 35(4): 537-547. DOI:10.1016/j.compgeo.2007.10.004 |
| [19] |
张子富, 杨文智, 朱海涛. 特高压输电线路杆塔基础承载力可靠度分析[J]. 天津大学学报(自然科学与工程技术版), 2015, 48(增刊1): 142-146. ( ZHANG Zifu, YANG Wenzhi, ZHU Haitao. Reliability analysis of bearing-capacity of tower foundations designed for ultra high voltage transmission lines[J]. Journal of Tianjin University (Science and Technology), 2015, 48(Suppl1): 142-146. (in Chinese)) |
| [20] |
TEIXEIRA A, HONJO Y, CORREIA A G, et al. Sensitivity analysis of vertically loaded pile reliability[J]. Soils and Foundations, 2012, 52(6): 1118-1129. DOI:10.1016/j.sandf.2012.11.025 |
| [21] |
洪昌华, 龚晓南. 基于稳定分析法的碎石桩复合地基承载力的可靠度[J]. 水利水运科学研究, 2000(1): 30-35. ( HONG Changhua, GONG Xiaonan. Relibility of bearing capacity of composite foundation based on stabilization analysis[J]. Journal of Nanjing Hydraulic Research Institute, 2000(1): 30-35. DOI:10.3969/j.issn.1009-640X.2000.01.005 (in Chinese)) |
2. College of Civil Engineering, Southeast University, Nanjing 210096, China
 2019
2019 