2. 工程防灾与结构安全教育部重点实验室, 广西 南宁 530004;
3. 广西防灾减灾与工程安全重点实验室,广西 南宁 530004
在氯化物环境中,外部环境中的氯离子会通过扩散等作用不断地向混凝土内部传输和积聚,当其含量在混凝土中达到一定限值时,就会引起钢筋锈蚀、混凝土开裂等耐久性问题[1]。因此,为了开展混凝土结构的耐久性分析与设计,有必要建立合理的氯离子扩散分析模型。
混凝土的氯离子扩散系数反映了氯盐环境下混凝土抵御氯离子渗透和扩散的性能。Collepardi[2]和Suryavanshi等[3]将Fick第二定律中的扩散系数视为常数分别建立了氯离子的一维和二维扩散解析模型。然而,随着龄期增加,水泥水化程度不断发展,混凝土变得更加密实,导致混凝土中氯离子扩散系数随龄期的增加而逐渐降低,具有明显的时变特性[4-8]。文献[9-13]对影响混凝土中氯离子扩散的诸多因素进行了分析和识别, 发现氯离子扩散系数的时变性是影响混凝土中氯离子扩散过程和含量分布的主要因素。杨绿峰等[14-15]研究了混凝土扩散系数时变特性对氯离子扩散过程的影响,提出了等效扩散时间和相应的氯离子扩散场计算长度表达式,据此建立了大型混凝土结构中氯离子时变扩散分析的简化模型。需要说明的是,上述氯离子扩散模型主要适用于常规的面形构件(一维扩散)和矩形构件(二维扩散),而不适用于圆形截面构件。
由于圆形截面混凝土构件的几何外形和外部暴露条件与常规面形构件(一维扩散)和矩形构件(二维扩散)具有显著差异,所以不能直接利用常规面形构件和矩形构件的氯离子扩散分析模型来描述圆形截面混凝土中的氯离子含量分布规律。文献[16-17]建立了圆形截面混凝土中氯离子扩散分析的数值模型,但是计算精度和计算效率依赖于空间离散网格尺寸和时间步长,且往往存在计算量较大、计算精度容易受模型参数取值影响等缺陷。为了克服数值模型的缺陷,文献[18]基于极坐标系中的氯离子常扩散控制方程,利用贝塞尔函数描述了圆形截面混凝土中的氯离子常扩散解析模型;文献[19]基于混凝土管桩的边界条件,考虑管桩内径和外径大小等因素的影响,采用分离变量法推导建立了混凝土管桩中氯离子的常扩散解析模型。但上述解析模型都假定氯离子扩散系数为常数,从而无法考虑时变性对氯离子扩散过程的影响。
鉴于此,本文考虑氯离子扩散系数的时变特性,在极坐标系下建立了圆形截面混凝土中氯离子时变扩散的控制方程,并通过引入等效扩散时间将氯离子的时变扩散方程转化为常扩散方程,进而利用变量代换对扩散方程的边界条件进行齐次化处理。然后利用变量分离法以及贝塞尔函数的正交性和递推性,建立了圆形截面混凝土中氯离子时变扩散的解析解,最后通过与数值模型对比分析验证了该方法的正确性。
1 氯离子时变扩散解析模型根据图 1所示的圆形截面混凝土构件几何形状及其在氯离子环境中的暴露条件,圆形截面混凝土中氯离子扩散的控制方程可描述为[18]:

|
图 1 圆形截面混凝土构件及其氯离子暴露条件 Fig.1 Circular section concrete members and their chloride exposure conditions |
| $ \frac{\partial C(r, t)}{\partial t}=D(t)\left(\frac{\partial^{2} C(r, t)}{\partial r^{2}}+\frac{1}{r} \frac{\partial C(r, t)}{\partial r}\right), (0 \leqslant r \leqslant R, t \geqslant 0) $ | (1) |
其边界条件和初始条件分别为:
| $ C(r=R, t>0)=C_{\mathrm{s}} ; C(r, t=0)=C_{0} $ | (2) |
式中:C(r, t)为t时刻圆形截面中到圆心O距离为r处的氯离子质量分数(占胶凝材料的质量百分数)(%);Cs为混凝土表面氯离子质量分数(%);C0为初始氯离子质量分数(%);r为圆形截面中任意点到圆心O的距离(mm);t为持续暴露于氯化物环境中的时间(a),简称暴露时间;R为圆心O到混凝土外表面的距离(mm),即圆形截面的半径;D(t)为混凝土中氯离子的时变扩散系数(mm2/a或m2/s),可以描述为[15]:
| $ D(t)=D_{0}\left(\frac{t_{0}}{t+t_{0}}\right)^{n}=D_{0} g(t) $ | (3) |
式中:t0为初始龄期(a);n为氯离子扩散系数的龄期衰减系数,简称龄期衰减系数;D0为混凝土在t0时刻的氯离子扩散系数,简称初始扩散系数(m2/s或mm2/a)。
为将式(1)描述的氯离子时变扩散方程变换为氯离子常扩散控制方程,可以基于式(3)定义等效暴露时间T的微分[11]:
| $ \frac{\mathrm{d} T}{\mathrm{d} t}=g(t)=\left(\frac{t_{0}}{t+t_{0}}\right)^{n} $ | (4) |
将式(4)等号两边同时在0到t范围内进行积分可得[11]:
| $ T=\int_{0}^{t} g(t) \mathrm{d} t=\int_{0}^{t}\left(\frac{t_{0}}{t+t_{0}}\right)^{n} \mathrm{d} t=\frac{t_{0}^{n}}{1-n}\left[\left(t+t_{0}\right)^{1-n}-t_{0}^{1-n}\right] $ | (5) |
根据式(4),式(1)的等号左边可变换为:
| $ \frac{\partial C(r, t)}{\partial t}=\frac{\partial C(r, t)}{\partial T} \frac{\mathrm{d} T}{\mathrm{d} t}=g(t) \frac{\partial C(r, t)}{\partial T} $ | (6) |
考虑到式(2)中第1式定义的边界条件的非齐次性,令:
| $ C(r, t)=U(r, t)+C_{\mathrm{s}} $ | (7) |
将式(3)、式(6)和式(7)代入式(1)和(2),可得:
| $ \frac{\partial U(r, t)}{\partial T}=D_{0}\left(\frac{\partial^{2} U(r, t)}{\partial r^{2}}+\frac{1}{r} \frac{\partial U(r, t)}{\partial r}\right), (0 \leqslant r \leqslant R, T \geqslant 0) $ | (8) |
对应的边界条件和初始条件分别为:
| $ U(r=R, T>0)=0 ; U(0 \leqslant r \leqslant R, T=0)=C_{0}-C_{\mathrm{s}} $ | (9) |
可以利用变量分离法求解式(8),令:
| $ U(r, t)=F(r) Z(T) $ | (10) |
式中:F(r)和Z(T)分别为圆形截面半径r和等效暴露时间T的函数。将式(10)代入式(8)可得:
| $ r^{2} F^{\prime \prime}(r)+r F^{\prime}(r)+\lambda r^{2} F(r)=0 ; Z^{\prime}(T)+D_{0} \lambda Z(T)=0 $ | (11) |
式中:F″(r)和F′(r)分别表示F(r)对r的二阶导数和一阶导数;Z′(T)表示Z(T)对T一阶导数;λ为常数,表示微分方程(11)的特征值。式(11)第2个方程的解为:
| $ Z(T)=A\operatorname{exp}\left(-D_{0} T \lambda\right) $ | (12) |
式中:A为常数;由于当T→∞时,U→0,所以λ>0。
式(11)的第1个方程为贝塞尔方程,存在以下级数解:
| $ F(r)=\sum\limits_{k=0}^{\infty} a_{k} r^{m+k}, a_{0} \neq 0 $ | (13) |
式中:m为常数;k=0, 1, 2,…, ∞;ak为常数。将式(13)代入式(11)的第1个方程可得:
| $ \begin{array}{l} {m^2}{a_0}{r^m} + {(m + 1)^2}{a_1}{r^{m + 1}} + \\ \sum\limits_{k = 2}^\infty {\left[ {{{(m + k)}^2}{a_k} + \lambda {a_{k - 2}}} \right]} \times {r^{m + k}} = 0 \end{array} $ | (14) |
由于式(14)为恒等式,所以可以求得式(14)中的系数为:
| $ a_{2 i-1}=0, \frac{a_{2 i}}{a_{0}}=\frac{(-\lambda)^{i}}{2^{2 i} \times(i !)^{2}}, (i=1, 2, 3 \cdots) $ | (15) |
根据式(9)中的边界条件,联合式(14)和式(15)可得:
| $ a_{0}\left(1+\frac{(-\lambda) R^{2}}{2^{2} \times(1 !)^{2}}+\frac{(-\lambda)^{2} R^{4}}{2^{4} \times(2 !)^{2}}+\cdots+\frac{(-\lambda)^{k} R^{2 k}}{2^{2} \times(k !)^{2}}+\cdots\right)=0 $ | (16) |
记0阶贝塞尔函数为:
| $ J_{0}(x)=1-\frac{x^{2}}{2^{2} \times(1 !)^{2}}+\frac{x^{4}}{2^{4} \times(2 !)^{2}}-\cdots+(-1)^{k} \frac{x^{2 k}}{2^{2 k} \times(k !)^{2}}+\cdots $ | (17) |
则由式(16)和式(17)可得:
| $ J_{0}(\sqrt{\lambda} \cdot R)=0 $ | (18) |
将满足式(18)的λ分别记为λ1,λ2,…,λi,则有:
| $ F_{i}(r)=a_{0} J_{0}(\sqrt{\lambda_{i}} \cdot r) ; Z_{i}(T)=A_{i} \exp \left(-D_{0} T \lambda_{i}\right) $ | (19) |
令λi=βi2,则可以得到式(8)的解为:
| $ U(r, t) = \sum\limits_{i = 1}^\infty {{A_i}} \exp \left( { - {D_0}T{{\left( {{\beta _i}} \right)}^2}} \right){J_0}\left( {{\beta _i}r} \right) $ | (20) |
结合式(9)中的初始条件可得:
| $ {C_0} - {C_{\rm{s}}} = \sum\limits_{i = 1}^\infty {{A_i}} {J_0}\left( {{\beta _i}r} \right) $ | (21) |
根据式(21)及贝塞尔函数的性质[18], 可以求得系数Ai的表达式为:
| $ A_{i}=-\frac{2\left(C_{\mathrm{s}}-C_{0}\right)}{\beta_{i} R J_{1}\left(\beta_{i} R\right)} $ | (22) |
结合式(7),(20)和(22)可以得到:
| $ \begin{array}{l} C(r, t) = {C_{\rm{s}}} - \sum\limits_{i = 1}^\infty {} \\ \frac{{2\left( {{C_{\rm{s}}} - {C_0}} \right)\exp \left( { - {D_0}\frac{{t_0^n}}{{1 - n}}\left( {{{\left( {t + {t_0}} \right)}^{1 - n}} - t_0^{1 - n}} \right)\beta _i^2} \right)}}{{{\beta _i}R{J_1}\left( {{\beta _i}R} \right)}}{J_0}\left( {{\beta _i}r} \right) \end{array} $ | (23) |
式中:βi可由λi=βi2及式(18)求出,分析表明,当i≥20时计算结果趋于稳定。
2 对比验证分析 2.1 解析模型的有效性验证分析某圆形截面钢筋混凝土桥墩的半径R=600 mm,混凝土中的初始氯离子质量分数C0=0.10%,混凝土表面氯离子质量分数Cs=5%,暴露于海水环境的初始龄期t0=28 d,氯离子扩散系数的龄期衰减系数n=0.5。要求采用解析模型分析圆形截面混凝土中的氯离子质量分数分布,并与基于有限元法的数值模型进行对比分析。以初始氯离子扩散系数D0=6×10-12 m2/s、暴露时间50 a为例,分别利用解析模型和传统数值模型计算距离混凝土表面扩散深度为50 mm处的氯离子质量分数,从而对比分析两种方法的计算精度和计算效率(见表 1)。由解析模型计算得到的氯离子质量分数为1.049%,计算耗时为0.322 s。由表 1可知,随着空间离散网格尺寸Δx和时间步长Δt的减小,数值模型的计算精度逐渐趋于稳定;当时间步长Δt不大于0.1 a、空间离散网格尺寸Δx不大于5.0 mm时,才能保证数值模型的计算精度,说明数值模型计算精度依赖于空间离散网格尺寸和时间步长;随着空间离散网格尺寸Δx和时间步长Δt的减小,数值模型的计算耗时逐渐增加,说明数值模型的计算效率依赖于空间离散网格尺寸和时间步长;当时间步长Δt取0.1 a、空间离散网格尺寸Δx取5.0 mm时,数值模型的计算耗时为753.75 s,为解析模型计算耗时的2 340倍。由此可见,所建的解析模型可以有效克服传统数值模型的计算精度和计算效率依赖于空间离散网格尺寸和时间步长所存在的缺陷。
| 表 1 空间离散网格和时间步长对数值模型计算精度与计算效率的影响 Tab.1 Influences of spatial discrete grids and time steps on calculation accuracy and efficiency of numerical model |
为进一步对比分析解析模型计算精度,考虑初始氯离子扩散系数分别取D0-1=2×10-12 m2/s, D0-2=4×10-12 m2/s, D0-3=6×10-12 m2/s, D0-4=8×10-12 m2/s和D0-5=10×10-12 m2/s共5种情况。利用解析模型分析当暴露时间t为30,50和100 a时圆形截面混凝土中的氯离子质量分数分布,并与数值模型(Δx和Δt分别取5.0 mm和0.1 a)的计算结果进行对比分析(见图 2)。图 2中,AM和NM分别表示解析模型和数值模型计算结果。由图 2可知,相同扩散深度处的氯离子质量分数随着D0的增加而逐渐增大;随着扩散深度增加,氯离子质量分数逐渐降低;在不同t和D0的情况下,解析模型和数值模型所计算的氯离子质量分数分布均较为吻合,从而验证了解析模型的计算精度和适用性。
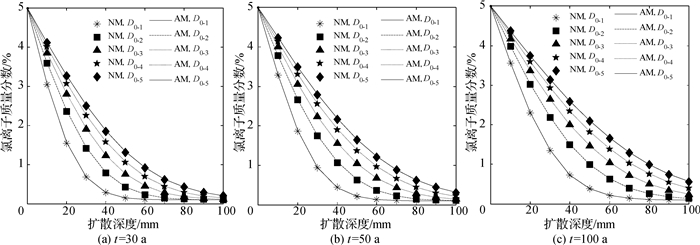
|
图 2 解析模型和数值模型所计算的氯离子质量分数分布比较 Fig.2 Comparison between chloride concentration distribution calculated by analytical and numerical models |
为分析式(17)中0阶贝塞尔函数的零点个数对解析模型计算精度的影响,考虑初始氯离子扩散系数分别取D0-1=2×10-12 m2/s,D0-2=4×10-12 m2/s,D0-3=6×10-12 m2/s,D0-4=8×10-12 m2/s和D0-5=10×10-12 m2/s等5种情况。0阶贝塞尔函数依次取5~100个零点时,计算距离混凝土表面扩散深度为50 mm处的氯离子质量分数(图 3)。由图 3可知,随着0阶贝塞尔函数零点个数的增加,解析模型计算结果逐步趋于稳定,当0阶贝塞尔函数的零点个数i≥20时,计算精度可以保证。
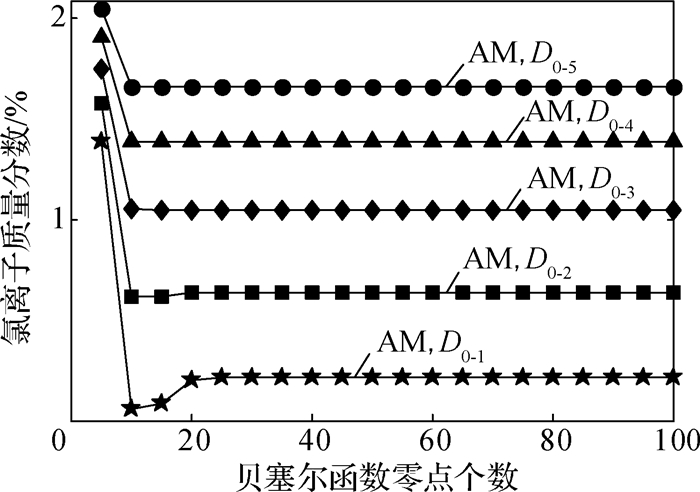
|
图 3 贝塞尔函数零点个数对解析模型计算精度的影响 Fig.3 Effects of zero numbers of zero-order Bessel functions on accuracy of analytical model |
以初始氯离子扩散系数D0=6×10-12 m2/s、暴露时间t为30,50和100 a为例,当龄期衰减系数n分别为0.2,0.3,0.4,0.5和0.6时,由解析模型计算的氯离子质量分数分布曲线与文献[18]中不考虑氯离子扩散系数时变性的模型(简称常扩散模型)所计算的氯离子质量分数分布曲线如图 4所示。由图 4可知,由于常扩散模型无法考虑氯离子扩散系数的时变衰减特性,导致所计算的氯离子质量分数明显偏高,当暴露时间和龄期衰减系数越大,高估现象越明显;当暴露时间相同时,随着龄期衰减系数n的增大,相同扩散深度处的氯离子质量分数逐渐降低,主要原因在于龄期衰减系数n越大,同一暴露时刻的氯离子扩散系数越小,从而导致相同扩散深度处的氯离子质量分数越低。
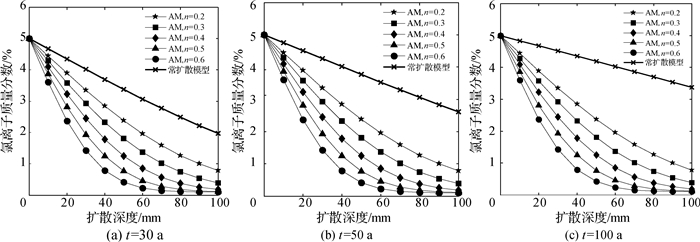
|
图 4 氯离子扩散系数时变性对氯离子质量分数分布的影响 Fig.4 Effects of time-dependent chloride diffusion coefficients on chloride concentration distribution |
以初始氯离子扩散系数D0=8×10-12 m2/s,龄期衰减系数n=0.3,暴露时间t为30 a,50 a和100 a,圆形截面混凝土构件的半径R为200,300,400,500和600 mm为例,利用解析模型计算不同半径圆形截面混凝土中的氯离子质量分数分布,并与文献[20]建立的二维(2-D)和一维(1-D)扩散解析模型计算的氯离子质量分数分布进行对比分析(图 5)。图 5中,C-200表示半径R=200 mm,其他符号类似。由图 5可知,圆形截面混凝土中的氯离子质量分数处于一维扩散和二维扩散之间;随着圆形截面半径的增大,氯离子质量分数分布逐渐趋近于一维扩散的情况;随着暴露时间增大,相同半径圆形截面混凝土中的氯离子质量分数分布与一维扩散的氯离子质量分数分布差异更加明显。
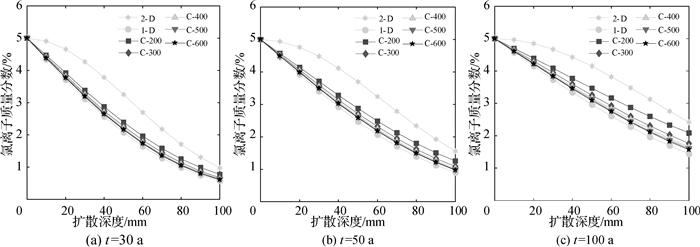
|
图 5 圆形截面半径对氯离子质量分数分布的影响 Fig.5 Effect of cross-section radius on chloride concentration distribution |
进一步以初始氯离子扩散系数D0=8×10-12 m2/s,混凝土表面氯离子质量分数Cs=5%,暴露时间t=30,50和100 a,龄期衰减系数n=0.2,0.4和0.6为例,分析不同半径的圆形截面与一维扩散情况下距离混凝土表面80 mm处的氯离子质量分数相对误差(表 2)。由表 2可知,随着截面半径和龄期衰减系数的增大,圆形截面与一维扩散的氯离子质量分数相对误差逐渐减小;随着暴露时间增加,圆形截面与一维扩散的氯离子质量分数相对误差逐渐增大。此外,以暴露年限t=50 a,龄期衰减系数n=0.4,初始氯离子扩散系数D0=2×10-12,6×10-12和10×10-12 m2/s,混凝土表面氯离子质量分数Cs=2.0%,3.5%和5.0%为例,分析不同半径的圆形截面与一维扩散情况下距离混凝土表面80 mm处的氯离子质量分数相对误差(见表 3)。由表 3可知,随着截面半径增大,圆形截面与一维扩散的氯离子质量分数相对误差逐渐减小;随着初始氯离子扩散系数和混凝土表面氯离子质量分数增加,圆形截面与一维扩散的氯离子质量分数相对误差逐渐增大。结合表 2和3可知,当截面半径不小于900 mm时,圆形截面与一维扩散的氯离子质量分数相对误差控制在5%以内,说明此时二者比较接近。
| 表 2 不同n, t和半径情况下圆形截面与一维扩散的氯离子质量分数相对误差 Tab.2 Relative errors of chloride concentration between 1D diffusion and circular cross-section with different n, t and radius |
| 表 3 不同D0, Cs和半径情况下圆形截面与一维扩散的氯离子质量分数相对误差 Tab.3 Relative errors of chloride concentration between 1D diffusion and circular cross-section with different D0, Cs and radius |
结合贝塞尔函数和变量代换法,建立了圆形截面混凝土中氯离子时变扩散解析模型,并分析了氯离子扩散系数时变性、圆形截面半径和暴露时间等因素对圆形截面混凝土中氯离子质量分数分布的影响规律。分析结果表明:
(1) 所建立的时变扩散解析模型具有较高计算精度和计算效率,不仅可以有效克服数值模型对空间离散网格和时间步长的依赖性,而且还可以克服传统常扩散模型由于忽略氯离子扩散系数时变衰减特性而高估圆形截面混凝土中氯离子质量分数所存在的缺陷。
(2) 圆形截面混凝土中的氯离子质量分数分布介于一维和二维扩散之间,随着圆形截面半径和龄期衰减系数的增大,圆形截面混凝土中的氯离子质量分数逐渐降低,且圆形截面混凝土中的氯离子质量分数逐渐趋近于一维扩散的状况;当截面半径不小于900 mm时,圆形截面与一维扩散的氯离子质量分数相对误差控制在5%以内,说明此时二者比较接近。
(3) 随着0阶贝塞尔函数零点个数的增加,解析模型计算结果逐步趋于稳定,当0阶贝塞尔函数的零点个数大于20时,解析模型计算精度可以得到有效保证。
| [1] |
王胜年, 汤雁冰, 杨海成, 等. 基于长期性能观测的海工混凝土结构耐久性研究的新思路[J]. 水运工程, 2017(10): 60-66. ( WANG Shengnian, TANG Yanbing, YANG Haicheng, et al. New idea on durability study of marine concrete structure based on long-term property observation[J]. Port and Waterway Engineering, 2017(10): 60-66. DOI:10.3969/j.issn.1002-4972.2017.10.012 (in Chinese)) |
| [2] |
COLLEPARDI M. Penetration of chloride ions into cement pastes and concrete[J]. Journal of the American Ceramic Society, 1972, 55(10): 534-535. DOI:10.1111/j.1151-2916.1972.tb13424.x |
| [3] |
SURYAVANSHI A K, SWAMY R N, CARDEW G E. Estimation of diffusion coefficients for chloride ion penetration into structural concrete[J]. ACI Materials Journal, 2002, 99(5): 441-449. |
| [4] |
窦雪梅, 余红发, 麻海燕, 等. 珊瑚混凝土在海洋环境中氯离子扩散实验[J]. 海洋工程, 2017, 35(1): 129-135. ( DOU Xuemei, YU Hongfa, MA Haiyan, et al. Experiment on chloride diffusion coefficient of coral concrete exposed to marine environment[J]. The Ocean Engineering, 2017, 35(1): 129-135. (in Chinese)) |
| [5] |
CASTALDO P, PALAZZO B, MARINIELLO A. Effects of the axial force eccentricity on the time-variant structural reliability of aging r.c. cross-sections subjected to chloride-induced corrosion[J]. Engineering Structures, 2017, 130: 261-274. DOI:10.1016/j.engstruct.2016.10.053 |
| [6] |
JUSTNES H, KIM M O, NG S, et al. Methodology of calculating required chloride diffusion coefficient for intended service life as function of concrete cover in reinforced marine structures[J]. Cement and Concrete Composites, 2016, 73: 316-323. DOI:10.1016/j.cemconcomp.2016.08.006 |
| [7] |
ZHANG J Z, ZHENG Y Y, WANG J D, et al. Chloride transport in concrete under flexural loads in a tidal environment[J]. Journal of Materials in Civil Engineering, 2018, 30(11): 04018285. DOI:10.1061/(ASCE)MT.1943-5533.0002493 |
| [8] |
ZHANG J Z, GUO J, LI D H, et al. The influence of admixture on chloride time-varying diffusivity and microstructure of concrete by low-field NMR[J]. Ocean Engineering, 2017, 142(9): 94-101. |
| [9] |
MAAGE M, HELLAND S, POULSEN E, et al. Service life prediction of existing concrete structures exposed to marine environment[J]. ACI Materials Journal, 1996, 93(6): 602-608. |
| [10] |
WANG Y, WU L, WANG Y, et al. Prediction model of long-term chloride diffusion into plain concrete considering the effect of the heterogeneity of materials exposed to marine tidal zone[J]. Construction and Building Materials, 2018, 159: 297-315. DOI:10.1016/j.conbuildmat.2017.10.083 |
| [11] |
TANG L P, GULIKERS J. On the mathematics of time-dependent apparent chloride diffusion coefficient in concrete[J]. Cement and Concrete Research, 2007, 37(4): 589-595. DOI:10.1016/j.cemconres.2007.01.006 |
| [12] |
余红发, 孙伟, 麻海燕, 等. 混凝土在多重因素作用下的氯离子扩散方程[J]. 建筑材料学报, 2002, 5(3): 240-247. ( YU Hongfa, SUN Wei, MA Haiyan, et al. Diffusion equations of chloride ion in concrete under the combined action of durability factors[J]. Journal of Building Materials, 2002, 5(3): 240-247. DOI:10.3969/j.issn.1007-9629.2002.03.008 (in Chinese)) |
| [13] |
LIANG M T, WANG K L, LIANG C H. Service life prediction of reinforced concrete structures[J]. Cement and Concrete Research, 1999, 29(9): 1411-1418. DOI:10.1016/S0008-8846(99)00109-X |
| [14] |
杨绿峰, 胡春燕, 陈正, 等. 混凝土中氯离子随机时变扩散过程和浓度分布[J]. 建筑材料学报, 2013, 16(2): 210-216. ( YANG Lufeng, HU Chunyan, CHEN Zheng, et al. Stochastic and time-dependent diffusion of chloride ion in concrete and its concentration distribution[J]. Journal of Building Materials, 2013, 16(2): 210-216. DOI:10.3969/j.issn.1007-9629.2013.02.005 (in Chinese)) |
| [15] |
YANG L F, MA Q, YU B. Analytical solution and experimental validation for dual time-dependent chloride diffusion in concrete[J]. Construction and Building Materials, 2018, 161: 676-686. DOI:10.1016/j.conbuildmat.2017.11.176 |
| [16] |
王显利, 吴智敏, 郑建军. 氯离子侵蚀圆形截面钢筋混凝土结构耐久性分析[J]. 东北林业大学学报, 2006, 34(2): 76-77, 108. ( WANG Xianli, WU Zhimin, ZHENG Jianjun. Durability analysis of reinforced concrete structure with circular section under chlorine anion corrosion[J]. Journal of Northeast Forestry University, 2006, 34(2): 76-77, 108. DOI:10.3969/j.issn.1000-5382.2006.02.028 (in Chinese)) |
| [17] |
唐敏康, 王霆, 何勇, 等. 圆形截面下混凝土中氯离子扩散的数值模拟[J]. 有色金属科学与工程, 2015, 6(3): 105-110. ( TANG Minkang, WANG Ting, HE Yong, et al. Numerical simulation of chloride ions diffusion at circular cross-section concrete[J]. Nonferrous Metal Science and Engineering, 2015, 6(3): 105-110. (in Chinese)) |
| [18] |
周明, 杨绿峰, 陈正, 等. 圆柱体混凝土构件中氯离子扩散的解析研究[J]. 水利水运工程学报, 2012(6): 38-43. ( ZHOU Ming, YANG Lufeng, CHEN Zheng, et al. Chloride diffusion in concrete component with circular section[J]. Hydro-Science and Engineering, 2012(6): 38-43. DOI:10.3969/j.issn.1009-640X.2012.06.007 (in Chinese)) |
| [19] |
杨博, 李镜培, 岳著文. 氯离子在混凝土桩中扩散的解析解[J]. 低温建筑技术, 2013, 35(2): 79-80. ( YANG Bo, LI Jingpei, YUE Zhuwen. Analytical solution of chloride ion diffusion in concrete piles[J]. Low Temperature Architecture Technology, 2013, 35(2): 79-80. DOI:10.3969/j.issn.1001-6864.2013.02.032 (in Chinese)) |
| [20] |
杨绿峰, 李冉. 混凝土中氯离子二维扩散规律的解析研究[J]. 水利水电科技进展, 2009, 29(3): 20-23. ( YANG Lufeng, LI Ran. Analytical study of two-dimensional diffusion of chloride ion in concrete[J]. Advances in Science and Technology of Water Resources, 2009, 29(3): 20-23. (in Chinese)) |
2. Key Laboratory of Engineering Disaster Prevention and Structural Safety of the Ministry of Education, Nanning 530004, China;
3. Guangxi Key Laboratory of Disaster Prevention and Engineering Safety, Nanning 530004, China
 2019
2019 
