岛礁是一种特殊的海岸形式，与常规海岸相比，通常由陡峭的礁前斜坡和相对平坦的礁坪组成。礁前斜坡坡比一般在1:10的量级^[1]，有时可达1:4.5甚至更大^[2]。不同岛礁的礁坪宽度也会存在一定变化，有的礁坪宽度可达几千米，例如澳大利亚Warraber岛^[3]的礁坪宽度约5 km，有的礁坪宽度仅为几十米，例如马尔代夫机场岛。

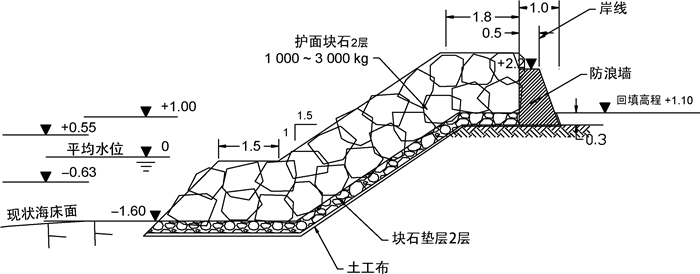
马尔代夫机场岛位于马尔代夫中部，紧邻其首都马累，属于珊瑚岛礁地形。马尔代夫机场岛护岸工程是马尔代夫机场改扩建工程的一部分。根据位置和地形的不同，护岸形式分为抛石式和板桩式。本文对抛石护岸稳定性进行研究。抛石护岸分布于机场西北侧，设计使用寿命为50年，总长度865 m，断面形式如图 1所示。现场地形测量资料显示：机场西北侧岸段岸坡较陡，坡度约为1:1.5~1:3.0，礁坪宽度较窄，约为20 m，高水位时礁坪水深为2~3 m。对于此类岛礁地形，波浪从深海传播至礁前斜坡时，水深急剧变浅，波浪变形严重，较大的波浪会在礁缘附近发生剧烈破碎，且大部分能量在破碎过程中得以消耗。因此这一区域的流态和动力条件十分复杂，会对护岸稳定性产生不利影响。

目前对于岛礁地形波浪动力特性的研究，多关注于波浪在礁坪上的传播^[4-6]、破碎^[7-9]、增水^{[2, 10-11]}、波生流^[12-14]等方面；而对岛礁地形上护岸工程稳定性的研究较少，尤其对于此类前沿岸坡较短的情况更是鲜有报道，对关键设计参数的认识较为缺乏。针对这一现状，以马尔代夫机场岛护岸工程为例，通过二维物理模型试验，对岛礁地形上抛石护岸稳定性进行研究，以期为今后同类工程设计提供借鉴参考。

1 试验设计 1.1 模型布置

试验在南京水利科学研究院波浪水槽中进行，水槽长60 m，宽1.8 m。水槽一端配有推板式造波机，并安装了二次反射波浪吸收装置。此外，在水槽两端均配有消浪缓坡及消浪设施，以减少波浪反射。试验水槽布置如图 2所示。试验采用正态模型，按Froude数相似律设计，模型比尺为1:10。

1.2 试验水深和波浪要素

试验波浪要素采用本工程《设计波浪要素推算报告》^[15]提供的计算结果。试验考虑了4种工况，工况1为50年一遇波浪+高水位(1.00 m)；工况2为50年一遇波浪+设计高水位(0.55 m)；工况3为50年一遇波浪+平均水位(0 m)；工况4为50年一遇波浪+设计低水位(-0.63 m)。各工况下原型和模型的波浪要素如表 1所示。由表 1可知，各水位下波浪要素相差不大。由于水槽水深限制，模型中礁前最大水深为1.4 m，即礁前地形从-13.0 m起算。为减少水深的影响，在试验结果分析阶段可将入射波高按线性理论换算成等效深水波高H₀，具体换算方法可参考《港口与航道水文规范》(JTS 145—2015)。^[16]

1.3 试验方法

试验中为得到目标波浪要素(表 1)，在正式试验前，需要先对波浪要素进行标定。标定过程中水槽内不摆放任何模型，仅在礁前斜坡坡脚处摆放1根波高仪(见图 2)，用于标定入射波浪要素大小。标定过程中，遵照《波浪模型试验规程》(JTJ/T 234—2001)^[17]，控制波普参数在误差范围以内，同时波高和周期模拟值与设计值的误差控制在±3%以内。在正式试验阶段，按标定的参数输入造波机控制系统进行造波。造波机每次连续造波个数不少于120个。

在波浪要素标定过程中，不规则波频谱采用JONSWAP谱，谱密度函数为：

$ S(f) = \frac{{\alpha {g^2}}}{{{{(2{\rm{ \mathsf{ π} }})}^4}}}\frac{1}{{{f^5}}}\exp \left[ { - 1.25{{\left( {\frac{{{f_{\rm{p}}}}}{f}} \right)}^4}} \right]r\exp\left[ {\frac{{{{\left( {f - {f_{\rm{p}}}} \right)}^2}}}{{2{\sigma ^2}f_{\rm{p}}^2}}} \right] $

(1)

式中：α为无因次常数；f_p为谱峰频率；r为谱峰升高因子，参照Yoshimi^[18]、俞聿修^[19]和柳淑学等^[7-8]的研究结果，r取3.3；σ为峰形参数量，f≤f_p时，σ=0.07，f>f_p时，σ=0.09。

完成波浪要素标定后，再在水槽内制作地形和摆放护岸模型。地形模拟采用等高线法进行圈围，偏差控制在±1 mm之内。护面块石质量经严格挑选，满足质量要求。模型检查无误后开始试验。每一工况累计试验持续时间不小于原型3 h，为保证试验结果的可靠性，每组试验至少重复3次。当3次重复试验的结果差别较大时，则增加重复次数。

1.4 关于护面块石稳定性的判别标准

护面结构失稳判别标准以《防波堤与护岸设计规范》(JTS 154—2018)^[20]中推荐的容许失稳率为标准。根据此规范护面块石抛填两层容许失稳率为1%~2%，即当滚动块石的个数超过护面块石总个数的2%时认为护面结构失稳。

2 断面稳定分析

试验考虑3种不同的岸坡宽度(见图 3)，即岸坡宽度取14.5，19.5和24.5 m。岸坡宽度为岸线至礁缘(-2.0 m高程)之间的距离。为方便表述，以下内容对上述3种岸坡宽度对应的断面分别称为试验断面1、试验断面2和试验断面3。

2.1 试验断面1

对于试验断面1，工况1试验测得7%左右块石发生明显滚动，滚动块石的质量为1 200~2 500 kg。失稳位置位于底部坡脚1.5 m宽平台附近。失稳原因为波浪在护岸坡脚附近发生破碎，水体直接冲击护面块石，冲击后的回流以及卷破波浪带动块石向外海滚动。工况2的护面块石失稳率为7%，失稳位置和失稳原因与工况1基本相同。与工况1和2相比，尽管工况3和4的波浪条件相差不大，但其水深有所减小，波浪破碎点向前(海侧)转移，卷破波对坡脚块石的冲击减弱，故未发生块石明显滚动。各工况的护面块石稳定情况见表 2。

2.2 试验断面2

对于试验断面2，工况1试验测得3%左右块石发生明显滚动，滚动块石的质量为1 200~2 500 kg。失稳位置及原因与试验断面1基本相同。工况2试验测得外坡坡脚处有2个块石发生滚动，占块石总数的2%。工况3和4的护面块石均无明显滚动。试验断面2在各工况下护面块石的稳定性如表 2所示。

相对于试验断面1，试验断面2的失稳块石数量有所减少。这主要是由于护岸前沿平台宽度有所增加，卷破波卷起的水体在传播过程中消耗了部分能量，对护面块石的冲击有所减弱。波浪在坡脚前沿的破碎情况如图 4所示。

2.3 试验断面3

对于试验断面3，工况1和2时护面块石无明显滚动，整体稳定无变形。工况3和4时护面块石无滚动，稳定。试验断面3在各工况下护面块石的稳定性如表 2所示。

相对于试验断面1和2，断面3护面块石满足稳定性要求。这主要是由于护岸前沿平台宽度进一步增加，卷破波在传播过程中，能量进一步消耗，且部分大波的主要破碎过程在到达护岸坡脚前已基本完成，故对护面块石的冲击进一步减弱。

3 护岸稳定影响因素分析

对比以上3个试验断面可知，岸坡宽度是影响护面块石稳定的重要因素之一。在同一工况下，岸坡宽度越宽对护面块石的稳定性越有利，因此，护岸断面应尽量靠后布置。但由于岛礁上空间有限(如本工程)，护岸布置过于靠后，势必会压缩岛礁空间资源；故还需探寻合理的平衡点，既可保证护岸工程的安全又可最大限度地释放岛礁空间资源。

由试验现象可知，外坡护面块石失稳主要是由波浪破碎(主要为卷破波)对块石冲击所造成的。若护岸布置于破碎点之后的一定区域(在此区域内破碎波部分能量得以消耗)，则可大大降低护面块石的失稳概率。对于岛礁地形上波浪起始破碎位置，Yao等^[21]曾进行过研究，但并未给出定量的计算方法。刘清君等^[22]根据二维模型试验，提出岛礁陡坡地形上波浪起始破碎点的计算式：

$ \frac{S}{H_{0}}=m^{-2.1}\left(\frac{m}{\sqrt{H_{0} / L_{0}}}\right)^{1.4}\left(\frac{h_{\mathrm{e}}}{d}\right)^{1.1} $

(2)

式中：S为波浪破碎点与礁缘之间的距离；d为坡前水深；h_e为礁坪水深，从礁缘起算；m为外坡坡度(m=tanβ，β为外坡与水平轴的夹角)；H₀为深水波高；L₀为深水波长，L₀=gT²/(2π)。

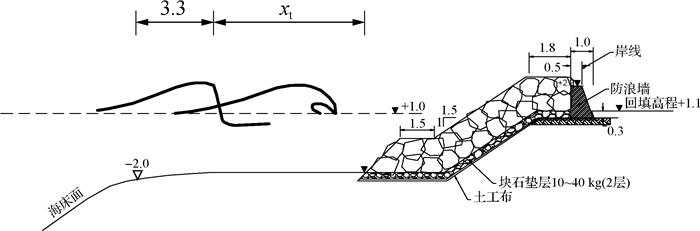
将式(2)应用于本工程破碎点计算，对于工况1，根据实际地形外坡坡度取1:1.5，根据《港口与航道水文规范》(JTS 145—2015)^[16]，斜坡式护面块石在稳定性设计中，设计波高累积频率标准为5%，即H_5%=2.53 m，经换算深水波高取2.59 m，深水波长取49.1 m，礁坪水深取礁缘处水深3.0 m，坡前水深取20 m，经计算破碎点距离为3.3 m，即波浪破碎点位于礁缘后3.3 m，进而可得护岸坡脚与破碎点之间的距离x_t。需要说明的是，上述破碎点为起始破碎点。对于卷破波，起始破碎点为波峰前坡面近乎垂直的位置。图 5给出了礁缘、破碎点和护岸坡脚三者之间的距离关系。

对于波浪在岛礁地形上的传播变形，浅水波长$ \sqrt{g h_{\mathrm{e}}}$是重要参数。研究表明，卷破长度x_p(起始破碎点与卷破点之间的距离)与浅水波长$ \sqrt{g h_{\mathrm{e}}}$大致相当^[23]，即x_p/($ \sqrt{g h_{\mathrm{e}}}$)≈1.0。Gourlay^[23]的研究表明，x_p/($ \sqrt{g h_{\mathrm{e}}}$)的变化范围为0.77~1.08。据此可以推断，护岸宜布置在破碎点之后1倍浅水波长范围之外。但对于某些工程(例如本工程)，限于空间位置，护岸前沿的岸坡宽度不能满足1倍浅水波长。故对于此类情况，护岸布置还需做进一步分析。

对比上述3个试验断面，分析各工况下护岸坡脚至破碎点的距离x_t和相对距离x_t/($ \sqrt{g h_{\mathrm{e}}}$)的变化，如表 3所示。当x_t/($ \sqrt{g h_{\mathrm{e}}}$)=0.26时，护面块石处于临界稳定状态；当x_t/($ \sqrt{g h_{\mathrm{e}}}$)>0.26时，护面块石处于稳定状态；当x_t/($ \sqrt{g h_{\mathrm{e}}}$) < 0.26时，护面块石大多处于失稳状态。具体情况可能与水深、波高等有关，还需要做进一步研究。为偏安全考虑，本试验将这一区域统一视为失稳状态。

综上所述，对于岛礁地形上斜坡式抛石护岸的布置，当前沿岸坡宽度允许时，护岸宜布置于破碎点之后的1倍浅水波长以外；当岸坡宽度较窄时，护岸宜布置于破碎点之后，并建议护岸坡脚与破碎点之间的距离不小于浅水波长的26%，即x_t/($ \sqrt{g h_{\mathrm{e}}}$)≥0.26。

4 结语

岛礁地形不同于常规海岸地形，由于其陡峭的外坡，外海或深水入射波浪在礁缘附近发生剧烈破碎，对抛石护岸的稳定性产生不利影响。其中，岸坡宽度是影响护岸稳定的重要因素。当护岸前沿岸坡宽度较宽时，护岸宜尽量靠后，布置于破碎点之后1倍浅水波长之外；当护岸前沿岸坡宽度较窄时，护岸宜布置于破碎点之后，且护岸坡脚与破碎点之间的距离不小于浅水波长的26%。

本文仅对护岸工程进行二维水槽模型试验研究。由于实际沿护岸长度方向的地形存在一定变化，同时还可能存在波浪斜向入射的问题，二维水槽试验不能反映沿岸地形变化，以及波浪斜向入射对护岸稳定性的影响，因此，可通过三维模型做进一步试验研究。另外，破碎波高、礁前斜坡坡度和长度也是影响岛礁地形上抛石护岸稳定的重要因素，建议今后亦可对此类问题进行深入研究。