2. 河海大学,江苏 南京 210098;
3. 苏州市河道管理处,江苏 苏州 215004
长江下游平原河网密布,河网对下游城市群的发展和水生态系统起着至关重要的作用,城市河网为人类提供生产生活用水,并兼具防洪排涝功能,改善城市景观。但长期以来,随着河网城市群城镇化与工业化的快速发展,入河污染物负荷增加。同时城市河网的自然形状过多地被人为改造,使得河网水动力条件恶化,不利于流入河网中污染物的迁移扩散,从而加剧了城市河网的污染[1-2]。近年来太湖流域的平原河网城市如苏州等地,通过建设一大批水工调控工程来控制并提高河网水动力,从而达到提升水质的效果。不同于天然河流,由于城市河流的水环境机理十分复杂,目前尚不完全明确。国内外学者在城市河网水环境方面开展了一些卓有成效的研究工作[3-7],发现透明度、浊度等指标在城市渠化河道中具有其独特的理化特征和形成机理[8]。有学者认为城市河道中的污染物大部分储存于河道悬浮物或沉积物中,在水动力变化的刺激下会向上覆水体释放或向水生生物迁移[9-12],并且水动力的变化也可能造成水体氧化还原的改变,从而促进碳酸盐的释放[13]。良好的流速条件也可以使河道内的水生植物更好地对营养盐进行吸收,进而抑制藻类过度生长[14]。目前国内外已有一些通过引调流提升水动力来改善城市局部河网水环境的实例[15-19]。但引调流工程带来的水动力提升对城市水环境的改善效应还无法被定量化,引水效益没有被很好地评估。因此,探索水动力条件的改变对河网水环境的改善影响,优化城市河网水质提升的闸泵调度方式,对太湖流域平原河网地区的社会经济可持续发展有着重要意义。
依托苏州古城区河网,基于野外原型观测结果,分析河网水环境特征,通过取样数据结合综合水质指数分析法(WQI)来讨论河网水质与流量条件变化之间的响应关系,分析变化流量条件下河网水质的分布特征及时空演变规律。量化苏州古城区河网引水调流所带来的水环境改善效果,为更加经济有效地提高苏州城区水环境质量提供技术支撑。
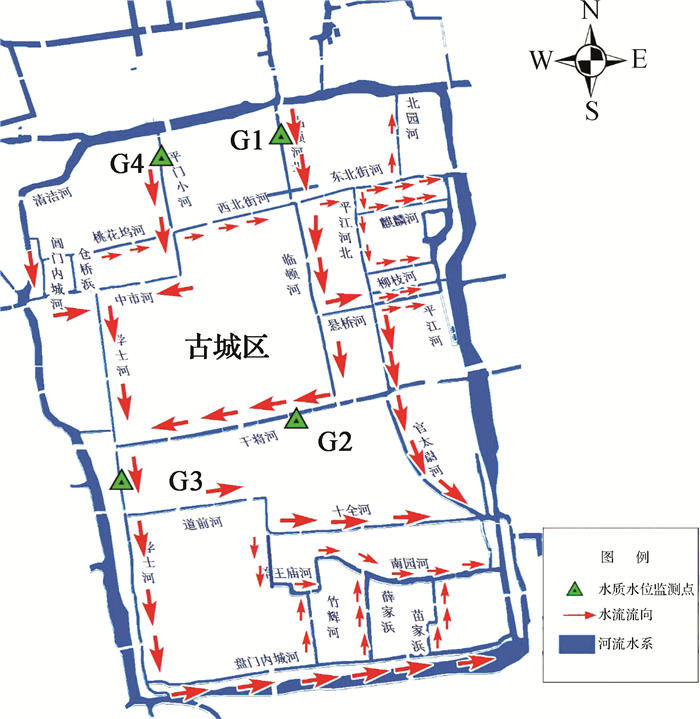
1 研究区域及原观方案苏州古城区位于苏州城市中心区域,面积14.2 km2,居住人口39.3万,河流总长度约34.72 km,其中包括“三横三直”骨干河道和阊门支流、平江水系、南园水系、其他内部河道等支河道。图 1为古城区现有河网水系结构情况。
|
图 1 古城区河网水系及引水监测示意 Fig.1 Water diversion monitoring in Suzhou river network |
2017年6月15日至7月10日,进行了苏州古城区河网调水原观试验研究。时逢太湖流域夏季汛期,河网来水资源十分充沛,满足试验的引水需求,苏州古城区内完善的河道闸泵工程也使得大部分河道的流量调控成为可能,为水动力提升和水质改善之间定量化关系提供一定的条件。河网内的水质状况受自身污染负荷和水体自净能力两方面作用影响。较好的水动力意味着河网水体的内部交换强度能够得到保证,有利于污染物的及时迁移。
调水试验在符合古城区防汛水位高度要求的前提下,设计齐门闸、平门闸、学士河南闸的低流量、中流量与大流量3种引调流方案。在试验方案的控制下,北环城河引流从古城区北面平门闸和齐门闸进入古城区河网,并在干将河汇合之后部分流入下游学士河。考虑到在整个河网流向上能实现基本覆盖,因而在水流方向上设置上游、中游、下游3个重要监测断面。断面名称分别为齐门河的堵带桥断面(断面G1)、干将河的太平桥断面(断面G2)及学士河的百花桥断面(断面G3),并在河流方向沿程也分布一系列的取样断面来监测水质沿程变化情况。其中堵带桥断面地处苏州拙政园风景区,断面前后无排污口,且离齐门闸进水口接近,可保证其水质一致性,因而在所有断面中属取样最佳断面。由于平门河水源与齐门河一样,都来自于北环城河,且同为古城区内南北向河流,因而设置平门河断面(断面G4),可作为良好的对照断面。水流方向如图 1所示。试验中水质取样于每日上午10:00与下午3:00进行,水质样品利用卡盖式采水圆筒于水面下50 cm处采集,并在2 h内送至实验室冷藏箱中避光低温保存。所采水样的水温(Tem)、溶解氧(DO)和pH等指标采用哈希HQ40d便携式多参数水质分析仪进行现场测定。其余水质指标参照标准化方法测定。试验采用ADCP进行流速流量率定,早上8:00至下午4:00间每小时1次,并同时记录水温与pH值。本次试验共获取水质数据512组,水动力数据1 134组。
本次研究中为将水动力变化以外因素的影响减小到最低,所有数据均在非雨天情况下收集。因6月20日至27日苏州当地有连续阵雨,故调水试验中断,此8天为非调水期。试验于6月28日恢复进行。由于汛期需求,齐门闸与平门闸进口流量无法同时低于4 m3/s。根据方案设定,6月15日至6月19日进口齐门河流量为3 m3/s,平门小河进口流量为4 m3/s,学士河南闸半开,6月28日至7月3日齐门河进口流量调整为4 m3/s,并于7月4日提高至5 m3/s。学士河南闸从7月1日起闸门全开。试验中的实际流量存在着小幅度的波动,流量情况见表 1。
| 表 1 流量调控方案 Tab.1 Flow control scheme |
原观试验期间古城区齐门河进水口的引水水源来自于连接外塘河的北环城河,相比于往年同期(2016年6月)的北环城河水质,以氨氮含量为例,在非引调水期间并无显著差别。水流经北环城河进入古城区后由于河道变窄、水深降低,水环境容量减小,因而污染物指标相对略高。意味着在水动力条件差的情况下,水环境容量减小,污染物在古城区内停留时间长是水环境问题的主要原因。调水前后的水质指标插值验证了这一点。正常情况下苏州河网的氨氮含量保持在Ⅴ类甚至更差。引水2天后,古城区内水质开始出现提升并逐渐进入稳态。前后两次调水原观时间连接紧密,水温受夏季气温影响,且变化不大,所有监测点水温都介于26.4~30.7 ℃。
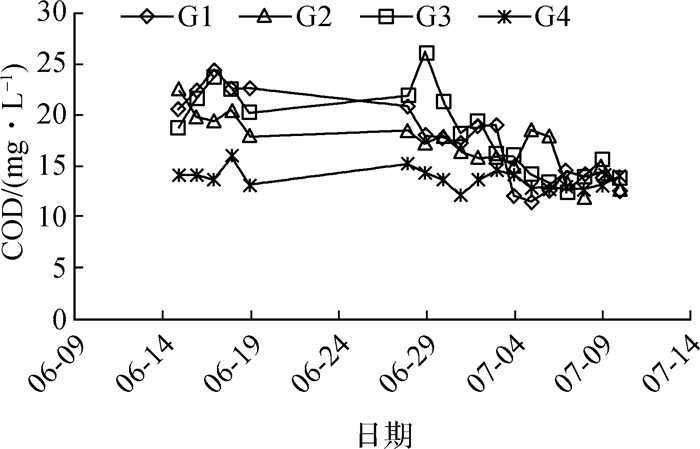
古城区进水口处的齐门河(G1)与平门小河(G4)的DO含量受水动力作用,较调水前有明显下降。在古城区中部的干将河处(G2)和南部的学士河处(G3)则变化略小。DO作为表征城市河网水体质量的重要指标,一定程度上反映了水体的自身净化能力,且当流速在0.2~0.4 m/s区间内水体不会产生明显的复氧变化。G2与G3的溶解氧曲线表明较高的污染物含量消耗了部分溶解氧。总体在各监测点中DO含量的空间变化分布为:G4>G1>G2>G3(图 2)。而氨氮含量随水动力变化的响应时间较DO相对滞后,且数据上随水动力的提升仅出现平缓的下降趋势。与DO相比,古城区各点位的氨氮含量变化率并不明显(图 3),其中G2干将河断面为调水前后下降最多的监测点位,下降幅度为23%。氨氮在水中的降解过程较为复杂。城市河网水体的氨氮主要来源于生活污水,它本身既是水体污染物,同时也是淡水系统中浮游生物生长所必需的营养盐。在古城区生活水动力的提升会促进水生植物对氨氮的吸收;在变化的水动力条件下,这种吸收作用经过2~3 d进入新的吸收稳态。同时在水体自净过程中,DO含量的增加会促进氨氮营养盐向硝酸根盐转化,因而氨氮含量与DO也存在自相关。氨氮本身也是水体中BOD降解过程中的中间产物,这也可能是响应水动力变化滞后的原因之一。根据调查统计,试验期间苏州古城区氨氮日排放量相对稳定,这也一定程度上造成指标值受试验流量调控方案影响较小。由图 4可知,古城区河网南部的COD指标偏高,且受引水量的影响较为明显,属于水动力响应敏感性指标;在一些时段中,与DO指标结果呈负相关性。一方面河网水体由北向南,流经学士河处污染物量已有一定的累积;另一方面,以学士河为典型的南面河流,一般情况下长期处于流动不明显状态。由图 4中各点位的COD指标比较可见,这种不流动状态可能比现场的视觉效果更为严重。而流动性较好的北面测点(G1,G4)也有明显的下降曲线,但在COD排放基值较小的情况下,峰值与谷值差别不大。引调流前后COD总体下降8.76 mg/L,学士河改善最优。

|
图 2 引流期间不同监测断面的DO指数变化 Fig.2 Changes of DO index at each monitoring site during drainage |

|
图 3 引流期间不同监测断面的氨氮指数变化 Fig.3 Changes of ammonia nitrogen index at each monitoring site during drainage |
|
图 4 引流期间不同监测断面的COD指数变化 Fig.4 Changes of COD index at each monitoring site during drainage |
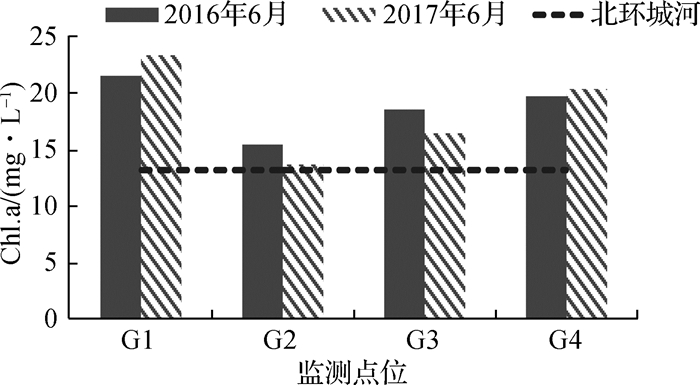
作为表征河网水体浮游植物生物量最常用的指标之一,叶绿素a含量(Chl.a)可以反映出藻类及浮游植物的现存量,通常与溶解氧指数一起作为衡量水体富营养化程度的指标。由此次试验所得数据(图 5)对比发现,古城河网内各监测点的含量空间分布差别不大,且古城区河网内各点调水前后的Chl.a含量均高于北环城河来水的Chl.a含量。引调流前后也没有鲜明的升高或降低变化,其中G1和G4的Chl.a含量高于调水前,G2和G3的Chl.a含量低于调水前。说明此次引调水在全面改善古城区河网DO的状态下并没有让Chl.a含量明显下降,表明在苏州河网中调水后Chl.a含量与DO缺乏显著的相关性。这与藻类在河网中分布的空间随机性有很大关系,短期的调水很难对城市河网中的藻类群落结构产生较大影响。前人的室内试验结果中显示水动力提升会产生一定的抑藻性效果[20],但在原型观测中实际上存在的其他干扰因子使得水动力提升对藻类的影响并不直观。
|
图 5 引流前后的监测断面叶绿素含量变化 Fig.5 Change of chlorophyll concentration at monitoring section after drainage |
基于本次试验所得实测数据,可利用污染物通量法分析监测断面在试验期间的水质变化情况。在实际的污染物通量计算过程中,原观实测时间段可直接采用实测数据,无实测资料时段可采用过程线趋势差值法计算。污染物通量通用计算式为:
| $ W = {\rm{ }}\int {Q\left( t \right)C\left( t \right){\rm{d}}t} $ | (1) |
式中:Q(t)为瞬时流量;C(t)为瞬时浓度。
但在实际原观过程中,想要获得连续的瞬时流量与污染物含量数据难度极大,只能获得一定时间间隔内的监测数据,因而在原观监测时段通量概化为:
| $ W = {Q_{\rm{a}}}{C_{\rm{a}}}T + \sum\limits_{i = 1}^n {Q_{_i}^nC_{_i}^n\Delta {t_i}} $ | (2) |
式中:Qa为时段平均流量;Ca为时段平均含量;T为计算时段;
式(2)中第1项为时均流量和时均含量的乘积,第2项为离散项。实际计算过程中,式(2)中离散项有关数据无法获得,所以采用如下简化计算过程:
| $ W = 0.003{\rm{ }}6\sum\limits_{i = 1}^n {\left( {\frac{{{C_i} + {C_{i + 1}}}}{2} \times \frac{{{Q_i} + {Q_{i + 1}}}}{2}{\rm{ }}} \right)({t_i} - {t_{i + 1}})} $ | (3) |
式中:通量结果以吨计;
试验期间各断面污染物通量计算结果如表 2所示。
| 表 2 试验监测断面污染物通量计算结果 Tab.2 Calculation results of pollutant flux in monitoring section |
根据表中污染物通量计算结果分析,在最大引水量方案下,各断面污染物通量削减率分别为15.2%(齐门河)、16.5%(平门小河)和13.2%(学士河)。
2.3 水动力改善效果的权重分析引水调度带来的水动力变化对古城区河网水质改善有两个方面的积极作用:一是引入来自西塘河的北环城河水进入古城区可有效提升古城区水环境质量;二是提升河道水体流动性可加快水中污染物的降解反应,进一步削减水体污染物含量。由原观监测数据表明,古城区北面齐门河(G1)与平门河(G4)的流速显著增加。如图 3和4所示,在水动力条件提升良好的两个点位,COD与DO受水动力提升影响显著,属敏感性因子。且由于断面条件的差别,在相同流量提升下,平门河(G4)的DO改善效果更优于齐门河(G1)。试验期间同比监测作为引水水源的外塘河的水质状况,发现除溶解氧外,外塘河的各项水质指标均优于古城区河网,这体现两处点位的溶解氧改善效果来自于水动力提升。同时,这也表明了水动力条件的变化与水质状况的改变存在一定的相关性。
然而受水系结构影响,引流带来的水动力提升效果在古城区河网空间上差异明显,在同等的闸泵工作条件下,学士河断面在所有监测断面中流量和水质改善效果最弱。在实际的原型观测中,河网各区域由于外界条件各异,即使在相同的水动力提升效果下,受原观的其他环境因子影响,水质情况也各不相同。因此对古城区河网而言,在其水动力与水质存在一定相关性的前提下,识别水动力因子在水质改善中的影响权重,显得尤为必要。
主成分分析(PCA)法为综合水质评价(water quality index,WQI)的环境因子权重计算方法[21]。该方法基于降低数据维度,在损失较少原始信息的前提下通过协方差计算将多个影响因子转变为几个主成分因子,进而解释多影响因素的数据内部结构,抓住主要权重并减少变量数目。最终可以压缩数据,提高分析效率[22]。适用于城市河网的WQI公式由Pesce和Wunderlin[22-23]提供,公式如下:
| $ {\rm{WQI}} = \sum\limits_{i = 1}^n {{C_i}{P_i}} /\sum\limits_{i = 1}^n {{P_i}} $ | (4) |
式中:n为试验中所分析水质参数的数量;Ci为水质指标标准化单位;Pi为水质指标的环境因子影响权重,由主成分分析法(PCA)计算。
参与权重评价的环境因子为流量、流速、温度和pH值,计算前首先将各因子的原始数据进行标准化处理,以便消除数据之间量纲与数量级的影响,利用的标准化公式为:
| $ x{\prime _{ij}} = ({x_{ij}} - {\mu _j})/{s_j}\;\;\;i = 1\;,\;2, \ldots ,m\;;j = 1\;,2\;, \ldots ,n $ | (5) |
式中:x′ij为处理后的标准化数据;xij为各因子的原始数据;μj,sj则分别为第j个因子指标样本的均值和标准差;m为因子的样本数量;n为指标数量。根据标准化后的各项数据计算相关系数矩阵R=(rij)n·n,该矩阵为n阶对称矩阵,相关系数rij的意义为第i个指标和第j个指标之间的相关程度大小,由下式计算可得:
| $ {r_{ij}} = \frac{{\sum\limits_{k = 1}^m {({x_{ki}} - {\mu _i})({x_{kj}} - {\mu _j})} }}{{\sqrt {{\rm{ }}\sum\limits_{k = 1}^m {{{({x_{ki}} - {\mu _i})}^2}} } \sum\limits_{k = 1}^m {{{({x_{kj}} - {\mu _j})}^2}} }}\;\;\;\;\;\;\;ij = 12 \ldots n $ | (6) |
从相关系数矩阵中可得出特征根与特征向量,其中特征根λi即为主成分Fi的方差。并通过计算方差贡献率来确定主成分,贡献率Ei即主成分Fi的方差占总方差的比重,环境因子的影响权重最终由主成分荷载值和主成分的方差贡献率决定,计算式为:
| $ {\omega _j} = (\sum\limits_{i = 1}^k {|{l_{ij}}|{E_i}} )/(\sum\limits_{j = 1}^r {\sum\limits_{i = 1}^k {|{l_{ij}}|} } {\rm{ }}) $ | (7) |
| $ {E_i} = {\lambda _i}/\sum\limits_{i = 1}^n {{\lambda _i}} $ | (8) |
| $ {l_{ij}} = {u_{ij}}/\;\sqrt {{\lambda _i}} \;\;\;\;i{\rm{ }}j = 12 \ldots n $ | (9) |
式中:ωj为第j个评价因子的权重[24];r为选取的评价因子数;lij为主成分荷载值。
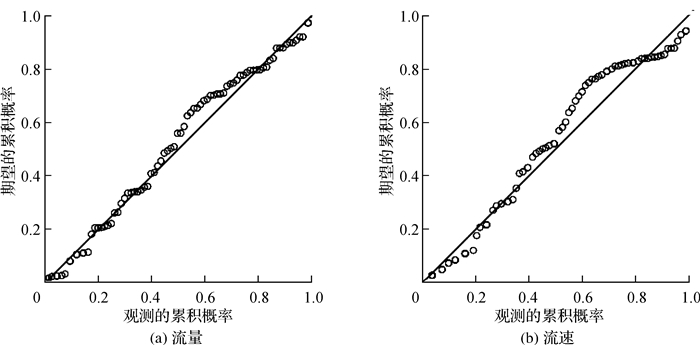
利用Spss软件对各环境因子的数据进行正态分布检验,检验结果如图 6所示,以流量(Q)和流速(V)两个环境因子为例,点离直线越近,或多数点都在直线上,表明数据有较好的正态性。
|
图 6 流量与流速数据的正态分布检验 Fig.6 Normal distribution test on data of flow and velocity |
依据标准化的水质相关数据,计算初选评价因子的相关系数矩阵,见表 3。通过表 3中数据显示,流速与DO,流量与COD,温度与DO及叶绿素含量,DO与COD,pH与氨氮含量相关性较强。
| 表 3 试验各项因子相关系数矩阵 Tab.3 Correlation coefficient matrix of each factor |
依据主成分因子协方差矩阵计算评价因子流量、流速、温度、pH对水质指标的权重,结果分别为0.145,0.141,0.109和0.089。权重计算结果与实测值通量计算结果趋势基本吻合,比较准确地反映了水动力提升后的河网水质状态。主成分分析结果表明,对于苏州古城区河网而言,增强河网水体流动性和水体交换是改善水质的可行办法,但权重影响并不那么突出。进一步改善古城南部区域的河网水质,需要基于更好的水利调度及水系结构优化方案。
3 结语对于苏州古城区而言,水环境质量状况随河网流量增大得到明显改善,这表明增强河网水体流动性是保证河网水质的有效方法之一。随着苏州防洪大包围网的建成,配合各河道密集的闸站设置及合理的调度,能够保证古城区河网一年四季下水量的总体稳定,污染物含量水平各季节保持相近。
在梯级调水方案条件下,齐门河、平门小河和学士河的总体污染物通量分别下降15.2%,16.5%和13.2%。古城区河网中COD和DO受水动力影响敏感性较强,可以作为当地的典型水质指标参数,较好地反映水动力调控的影响效果,并对调控方案有很好的指导作用。在试验研究过程中,古城区河网水体中氨氮含量变化受水动力影响较小,如需进一步削减苏州古城区河网水体的氨氮含量,则需寻求其他有效方法。
| [1] |
GERSHENFELD N, KRIKORIAN R, COHEN D. The internet of things[J]. Scientific American, 2004, 291(4): 76-81. DOI:10.1038/scientificamerican1004-76 |
| [2] |
GUNTHER O, KLETTI W, KUBACH U. RFID in manufacturing[M]. Berlin: Springer, 2008.
|
| [3] |
CHAOUNI A. River remediation and urban dvelopment scheme[R].Morocco: Global Holcim Awards, 2009.
|
| [4] |
刘静玲, 曾维华, 曾勇. 海河流域城市水系优化调度[M]. 北京: 科学出版社, 2008. ( LIU Jingling, ZENG Weihua, ZENG Yong. Optimal regulation of urban water system in Haihe River Basin[M]. Beijing: Science Press, 2008. (in Chinese))
|
| [5] |
李乃文, 齐兴云. 聊城市水安全问题的研究与对策[J]. 地下水, 2009, 31(4): 68-70. ( LI Naiwen, QI Xingyun. Research and countermeasures on water safety in Liaocheng City[J]. Groundwater, 2009, 31(4): 68-70. DOI:10.3969/j.issn.1004-1184.2009.04.023 (in Chinese)) |
| [6] |
林晶. 福州市城区内河引闽冲污后水质变化趋势及防治对策[J]. 环境监测管理与技术, 2005, 17(2): 21-23, 27. ( LIN Jing. Water quality change and control of inner river of Fuzhou urban reban region after water of Mingjiang was lead to reduce pollution[J]. The Administration and Technique of Environmental Monitoring, 2005, 17(2): 21-23, 27. DOI:10.3969/j.issn.1006-2009.2005.02.007 (in Chinese)) |
| [7] |
HEDDAM S. Secchi disk depth estimation from water quality parameters: artificial neural network versus multiple linear regression models[J]. Environmental Processes, 2016, 3(2): 525-536. DOI:10.1007/s40710-016-0144-4 |
| [8] |
ROBERTS D A. Causes and ecological effects of resuspended contaminated sediments(RCS) in marine environments[J]. Environment International, 2012, 40: 230-243. DOI:10.1016/j.envint.2011.11.013 |
| [9] |
金相灿, 尚榆民, 徐南妮, 等. 湖泊富营养化控制与管理技术[M]. 1版. 北京: 化学工业出版社, 2001: 87-89. ( JIN Xiangcan, SHANG Yumin, XU Nanni, et al. Lake eutrophication control and management technology[M]. 1st ed. Beijing: Chemical Industry Publishing, 2001: 87-89. (in Chinese))
|
| [10] |
彭近新, 陈慧君. 水质富营养化与防治[M]. 1版. 北京: 中国环境科学出版社, 1988: 97-115. ( PENG Jinxin, CHEN Huijun. Water quality eutrophication and prevention[M]. 1st ed. Beijing: China Environmental Press, 1988: 97-115. (in Chinese))
|
| [11] |
朱广伟, 秦伯强, 高光. 风浪扰动引起大型浅水湖泊内源磷暴发性释放的直接证据[J]. 科学通报, 2005, 50(1): 66-71. ( ZHU Guangwei, QIN Boqiang, GAO Guang. Direct evidence of explosive release of endogenous phosphorus in large lagoons caused by wind and waves disturbance[J]. Chinese Science Bulletin, 2005, 50(1): 66-71. DOI:10.3321/j.issn:0023-074X.2005.01.013 (in Chinese)) |
| [12] |
ZHANG C, YU Z G, ZENG G M, et al. Effects of sediment geochemical properties on heavy metal bioavailability[J]. Environment International, 2014, 73: 270-281. DOI:10.1016/j.envint.2014.08.010 |
| [13] |
杨倩倩, 吴时强, 吴修锋, 等. 引水对梅梁湾水质及浮游藻类影响的模拟研究[J]. 水生态学杂志, 2015, 36(4): 42-49. ( YANG Qianqian, WU Shiqiang, WU Xiufeng, et al. Effects of simulated water diversion on water quality and phytoplankton community in Meiliang bay[J]. Journal of Hydroecology, 2015, 36(4): 42-49. (in Chinese)) |
| [14] |
贾海峰, 杨聪, 张玉虎, 等. 城镇河网水环境模拟及水质改善情景方案[J]. 清华大学学报(自然科学版), 2013, 53(5): 665-672, 728. ( JIA Haifeng, YANG Cong, ZHANG Yuhu, et al. Simulations of a water quality improvement for urban river networks[J]. Journal of Tsinghua University (Science and Technology), 2013, 53(5): 665-672, 728. (in Chinese)) |
| [15] |
梅新敏, 阮晓红, 张兰芳, 等. 调引太湖水改善苏州市水动力条件研究[J]. 环境科学与管理, 2006, 31(1): 60-62. ( MEI Xinmin, RUAN Xiaohong, ZHANG Lanfang, et al. Research of water diversion from Taihu Lake to improve the water environmental in Suzhou[J]. Environmental Science and Management, 2006, 31(1): 60-62. DOI:10.3969/j.issn.1673-1212.2006.01.021 (in Chinese)) |
| [16] |
阮仁良.平原河网地区水资源调度改善水质的机理和实践研究——以上海市水资源引清调度为例[D].上海: 华东师范大学, 2003. (RUAN Renliang. Study on mechanism and practice of improving water qyuality by water resources diversion in plain river-net areas—A case study of the clean water diversion in Shanghai[D]. Shanghai: East China Normal University, 2003. (in Chinese))
|
| [17] |
刘丽.福州江北城区引清补水及调控研究[D].天津: 天津大学, 2012. (LIU Li. Study on the regulation and control of clean water diversion in Fuzhou urban area[D]. Tianjin: Tianjin University, 2012. (in Chinese))
|
| [18] |
顾孝荣. 提高水动力以改善城市水环境的方案探索[J]. 城市建设理论研究(电子版), 2012(16): 1. ( GU Xiaorong. Exploration of schemes to improve hydrodynamics to improve urban water environment[J]. Theoretical Research in Urban Construction(E-Edition), 2012(16): 1. (in Chinese)) |
| [19] |
杜军凯, 傅尧, 李晓星. 模糊-主成分分析综合评价法在地下水水质评价中的应用[J]. 中国环境监测, 2015, 31(4): 75-81. ( DU Junkai, FU Yao, LI Xiaoxing. Application of fuzzy comprehensive evaluation method-principal component analysis to groundwater quality evaluation[J]. Environmental Monitoring in China, 2015, 31(4): 75-81. DOI:10.3969/j.issn.1002-6002.2015.04.013 (in Chinese)) |
| [20] |
吕学研.调水引流对太湖富营养化优势藻的生长影响研究[D].南京: 南京水利科学研究院, 2013. (LV Xueyan. Impact of water diversion on the growth of dominant eutrophic algae in Lake Taihu[D]. Nanjing: Nanjing Hydraulic Research Institute, 2013. (in Chinese))
|
| [21] |
DEBELS P, FIGUEROA R, URRUTIA R, et al. Evaluation of water quality in the Chillán river (Central Chile) using physicochemical parameters and a modified water quality index[J]. Environmental Monitoring and Assessment, 2005, 110(1/3): 301-322. |
| [22] |
PESCE S F, WUNDERLIN D A. Use of water quality indices to verify the impact of Córdoba City (Argentina) on Suquía River[J]. Water Research, 2000, 34(11): 2915-2926. DOI:10.1016/S0043-1354(00)00036-1 |
| [23] |
韩晓刚, 黄廷林, 陈秀珍. 改进的模糊综合评价法及在给水厂原水水质评价中的应用[J]. 环境科学学报, 2015, 33(5): 1513-1518. ( HAN Xiaogang, HUANG Tinglin, CHEN Xiuzhen. Improved fuzzy synthetic evaluation method and its application in raw water quality evaluation of water supply plant[J]. Acat Scientiae Circumstantiae, 2015, 33(5): 1513-1518. (in Chinese)) |
| [24] |
代雪静, 田卫. 水质模糊评价模型中赋权方法的选择[J]. 中国科学院研究生院学报, 2011, 28(2): 169-176. ( DAI Xuejing, TIAN Wei. Choice of determining weights method in fuzzy synthetic evaluation model for water quality[J]. Journal of Graduate School of the Chinese Academy of Sciences, 2011, 28(2): 169-176. (in Chinese)) |
2. Hohai University, Nanjing 210098, China;
3. River Management Office of Suzhou, Suzhou 215004, China
 2019
2019 
