2. 防灾减灾湖北省重点实验室(三峡大学),湖北 宜昌 443002
目前关于冻融劣化混凝土力学特性研究,已进行了大量的试验和理论分析。Hasan等[1]展开了对冰冻损伤混凝土在疲劳荷载作用下的抗压试验研究,得到了试验应力-应变关系曲线。Penttala等[2]基于热力学和线弹性理论,计算了湿混凝土在冻融循环过程中的压力、应力和应变。刘博文等[3]进行了不同冻融循环次数混凝土的单轴压缩试验,并分析了其损伤演化规律与破坏机理。柳琪等[4]对冻融劣化混凝土进行了不同应变速率作用下的单轴循环加卸载试验,定义了混凝土的单轴循环加卸载耗散能、弹性应变能和塑性应变能,研究了这3种能量与冻融循环次数和循环加卸载次数之间的关系。曹大富等[5]对冻融循环后不同强度等级的混凝土进行单轴受拉和劈拉性能试验,分析了混凝土受拉性能随混凝土强度等级和冻融次数的变化规律,建立了冻融后混凝土受拉峰值应力与劈拉强度的关系式。徐童淋等[6]进行了不同冻融循环次数后混凝土在不同加载速率作用下的单轴动态抗压强度试验,分析了冻融劣化后混凝土的质量损失、动态抗压强度和峰值应变。覃丽坤等[7-8]研究了冻融循环后混凝土在不同拉压比下的双轴拉压强度和变形性能,在八面体应力空间和主应力空间构建了同时考虑冻融循环次数和拉压比的混凝土双轴拉压破坏准则;王立成等[9]对海水中不同冻融循环次数后的轻骨料混凝土进行双轴压强度试验,分析了冻融循环次数和应力比对极限抗压强度、峰值应变及应力-应变关系的影响,建立了考虑海水冻融作用的双轴压破坏准则。宋玉普等[10]通过对4种冻融循环次数后的混凝土进行5种不同应力比作用的双轴压试验,探讨了冻融混凝土在不同应力比作用下的弹性模量、双轴受压强度和变形的变化规律,并建立了双轴压破坏准则。
综上所述,国内外学者针对冻融劣化混凝土剪切强度方面的研究比较少,且多以常态混凝土研究其剪切特性。因此,本文旨在开展压剪复合应力状态下冻融劣化混凝土的试验研究,并对考虑冻融循环作用的混凝土压剪破坏准则加以探讨,为处于复杂应力状态下的水工混凝土建筑物结构设计提供基础数据与理论依据。
1 试验概况 1.1 试件制作依据《水工混凝土配合比设计规程》(DL/T 5330—2015),按C30强度等级进行设计,即水:水泥:砂:石= 0.60:1.00:2.33:4.32。水泥采用葛洲坝集团水泥有限公司生产的P·O 42.5级普通硅酸盐水泥;粗骨料为粒径5~40 mm的连续级配碎石,其中小石(粒径5~20 mm)和中石(粒径20~40 mm)质量比例为4:6;细骨料为连续级配的人工砂,实测细度模数为2.3;拌合水为饮用自来水。混凝土材料用量:水175.0 kg/m3,水泥291.0 kg/m3,砂676.9 kg/m3,小石502.8 kg/m3,中石754.3 kg/m3。
混凝土试件在300 mm×300 mm×300 mm的立方体钢模中成型,振捣密实、浇筑表面抹平后室内放置24 h后脱模,然后放入标准养护室(相对湿度≥95%,温度(20±2)℃)中养护28 d,试件龄期90 d,其单轴抗压强度为48.3 MPa。
1.2 快速冻融试验方法冻融设备为TR-TSDRSL型冻融循环试验机,混凝土冻融循环试验方法按照《普通混凝土长期性能和耐久性试验方法标准》(GB/T 50082—2009)中抗冻性能试验进行,冻融循环次数为0,10,25,35和50次,冻融循环1次需要14~16 h,其中冻结时间为8~9 h,融化时间为6~7 h。正式试验前对冻融试件表面进行打磨,以消除试件表面冻融产生的误差。
1.3 试验过程试验在10 MN微机控制电液伺服大型多功能动静力三轴仪试验机上完成。试验步骤如下:
(1) 装样:将试件抬至剪切盒底板中心处,调整试件位置让各侧面与剪切盒紧贴,紧固螺丝固定。
(2) 预加载:将剪切盒推入到试验机的作动器轴中心,然后双向施加10 kN的荷载预加载,让三轴仪的传力柱、剪切盒和试件三者能充分接触,同时使试件受到较小荷载的紧密挤压,确保正式加载时油缸压力能连续加载到试件上。
(3) 正式加载:竖向方向按照荷载控制方式对试件分别施加0,3,6,9和12 MPa的轴向法向应力并保持恒定;然后按照变形控制方式,水平方向以静态加载速率0.18 mm/min加载,直至得到包含下降段的完整剪切荷载-位移曲线,如图 1所示。

|
图 1 剪切荷载-位移全曲线 Fig.1 Shear load-displacement curve |
(4) 卸载:得到完整的剪切荷载-位移曲线后,停止加载,开始卸荷,保存试验数据。
2 试验结果与分析 2.1 强度性能通过试验,得到了不同冻融循环次数后混凝土在不同法向应力状态下的剪切强度试验结果(表 1)。混凝土在不同法向应力状态下的剪切强度与冻融循环次数的关系见图 2,不同冻融循环次数后混凝土剪切强度与法向应力的关系见图 3。
|
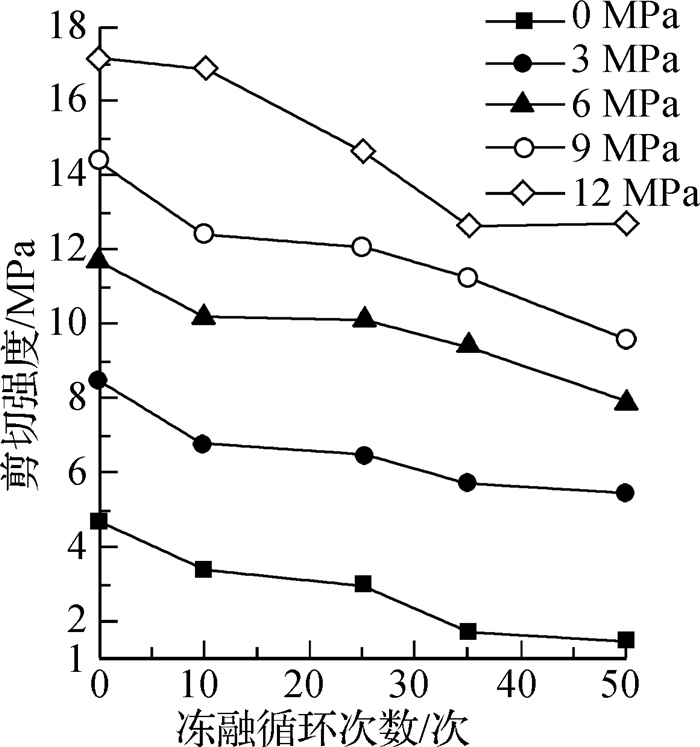
图 2 不同法向应力下剪切强度与冻融循环次数的关系 Fig.2 Relationships between shear strength of concrete and freeze-thaw cycle times under different normal stresses |
|
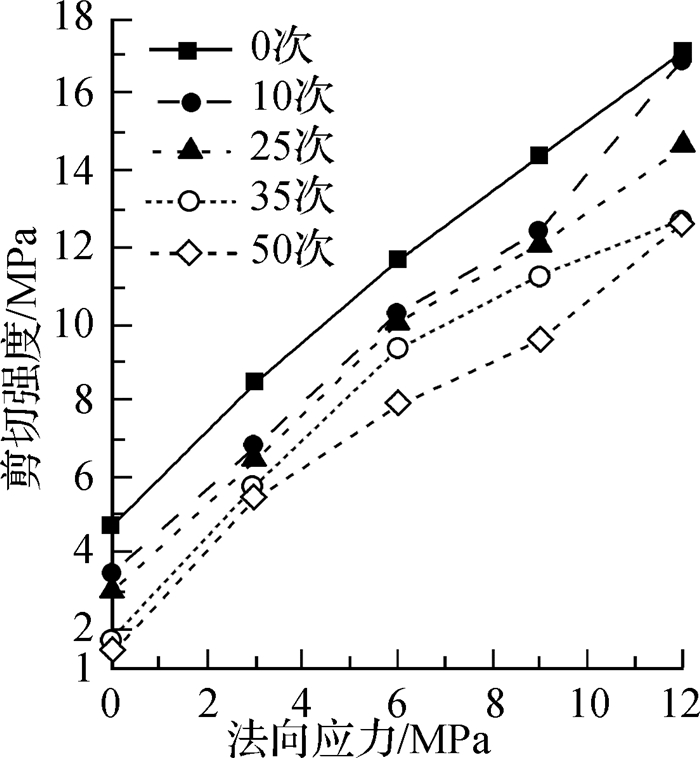
图 3 不同冻融循环次数后剪切强度与法向应力的关系 Fig.3 Relationships between shear strength of concrete and normal stress after different freeze-thaw cycle times |
| 表 1 不同冻融循环次数和法向应力水平下混凝土剪切强度 Tab.1 Shear strength of concrete under different freeze-thaw cycle times and normal stress levels |
从图 2可以看出,当冻融循环次数相同且法向应力不大于单轴抗压强度的50%时,混凝土的剪切强度随法向应力的增大而增大,法向应力的存在提高了混凝土的剪切强度。此外,随着冻融循环次数的增加,混凝土剪切强度在各种法向应力状态下的剪切强度均呈逐渐降低趋势,而且法向应力越大,剪切强度随冻融循环次数的增加而降低的程度越小。产生这种现象的原因在于:混凝土冻结时,试件内部微孔隙中的自由水会冻结成冰,体积膨胀,产生的冻胀力对微孔隙产生挤压力,导致孔隙逐渐扩展或形成微裂缝;融化时,自由水在混凝土孔隙和微裂缝中移动,对孔隙和微裂缝产生水压力,进而损坏孔隙和裂缝间的颗粒。由于混凝土材料的不均匀性,在冻融劣化反复作用下,混凝土内部微孔隙急剧增多、裂缝迅速扩展而贯通,从而导致混凝土内部孔隙结构被改变,孔隙率急剧增大,冻融循环作用越多,混凝土孔隙率越大[11-12],从而减小了混凝土有效受力面积,导致混凝土剪切强度随冻融劣化程度的加深而降低,这与文献[13]所得出的混凝土强度随孔隙率增大而降低的结论一致。
从图 3可见,冻融循环次数相同时,混凝土剪切强度随法向应力的增大而增大,且随着冻融循环次数的增加其法向应力对剪切强度的增幅效果会有所降低,也影响压剪耦合关系曲线形状。随着法向应力增大,在法向应力为6 MPa时,压剪耦合关系曲线从线性增长过渡到非线性增长;另外,随着冻融循环次数的增加,压剪耦合关系从线性增长到非线性增长临界点有降低趋势。在冻融循环0次,法向应力为0~12 MPa时,压剪耦合关系为严格线性增长;而冻融循环10~50次时,可见法向应力6 MPa为线性增长与非线性增长临界点,在法向应力小于6 MPa时,剪切强度随法向应力增加呈正相关性关系,而在法向应力大于6 MPa时,剪切强度随法向应力的增加呈非线性增加。
以上规律是在较低法向应力状态下得出的,在高法向应力状态下,则不一定适用。
2.2 变形性能图 4为混凝土在不同法向应力状态下剪切峰值变形随冻融循环次数的变化规律,从图 4可见,在法向应力水平相同时,随着冻融循环次数的增加,混凝土剪切峰值变形逐渐增大,而且法向应力的增大提高了剪切峰值变形变大的能力,在冻融循环25次后迅速增加(水饱和状态除外);另外,在法向应力较低时(0~3 MPa),峰值变形增幅效果不大。
|
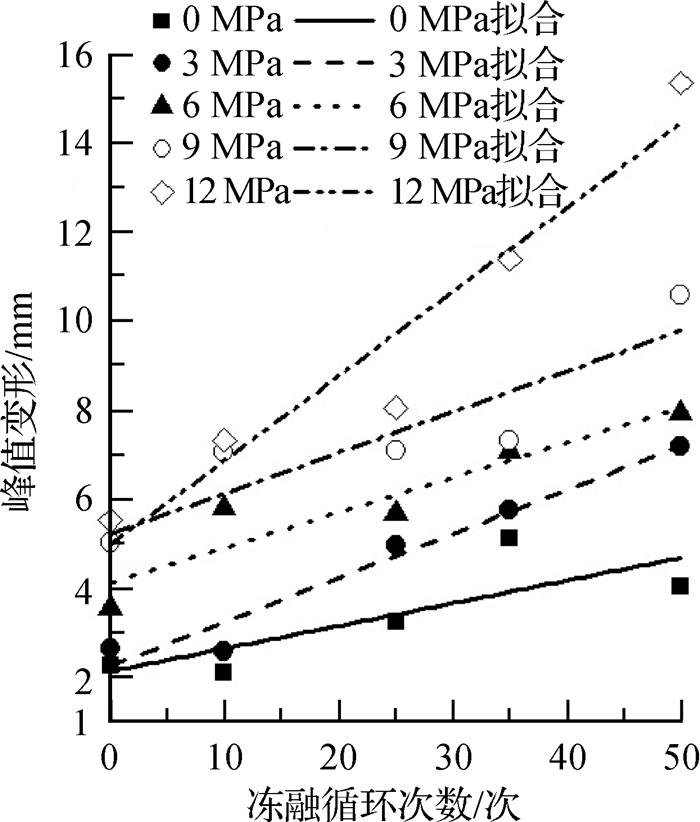
图 4 不同法向应力下剪切峰值变形与冻融循环次数的拟合 Fig.4 Fitting curves of shear peak deformation and freeze-thaw cycles under different normal stresses |
对图 4中不同法向应力下剪切峰值变形与冻融循环次数的关系采用线性表达式描述:
| $ {\delta _{{\rm{pd}}}} = {D_1} + {D_2}N $ | (1) |
式中:δpd为混凝土剪切峰值变形;D1,D2为线性回归系数;N表示冻融循环次数。分别对不同法向应力下剪切峰值变形进行经验回归分析,可得剪切峰值变形与冻融循环次数的关系式及相关系数:法向应力为0, 3, 6, 9, 12 MPa时,可决系数R2分别为0.832 9,0.946 0,0.837 6,0.758 6和0.908 4。经验回归直线与本文试验数据的比较见图 4。由图 4可见,式(1)能够较好地反映不同法向应力下剪切峰值变形与冻融循环次数之间的关系,二者吻合程度较好。
图 5为混凝土在不同冻融循环次数后剪切峰值变形随法向应力的变化规律。
|
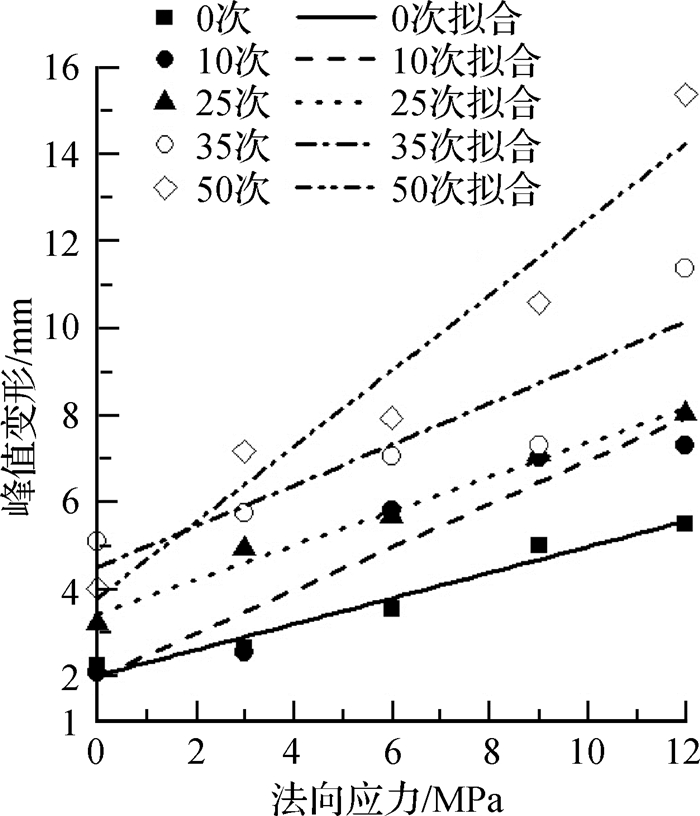
图 5 不同冻融循环次数后剪切峰值变形与法向应力的拟合 Fig.5 Fitting curves of shear peak deformation and normal stress after different freeze-thaw cycles |
从图 5可见,在冻融循环次数相同时,剪切峰值变形随法向应力的增大呈逐渐增加趋势,但在6 MPa以后,峰值变形迅速增加;在冻融循环次数相同时,剪切峰值变形随法向应力的关系曲线斜率不同,说明法向应力会影响混凝土变形能力。
对图 5中不同冻融循环次数后剪切峰值变形与法向应力的关系采用线性关系描述:
| $ {\delta _{{\rm{pd}}}} = {k_1} + {k_2}\sigma $ | (2) |
式中:k1,k2为线性回归系数;σ为法向应力。由本文试验数根据经验回归计算得到冻融循环次数分别为0,10,25,35和50次时,式(2)中的回归系数k1分别为2.033 1,2.001 1,3.448 6,4.516 1和3.810 9;回归系数k2分别为0.295 2,0.495 4,0.392 1,0.468 3和0.867 5;可决系数R2分别为0.951 0,0.876 2,0.982 0,0.773 3和0.923 4。经验回归直线与本文试验数据的比较见图 5,二者吻合程度较好。
2.3 剪切黏聚力和摩擦系数与冻融循环次数的关系当法向应力不大时,混凝土剪切强度可以用莫尔-库仑准则[14-15]表示。因此,将表 1中不同冻融循环次数后混凝土剪切强度与法向应力之间的试验结果按式(3)进行回归分析。
| $ \tau = \sigma {f^\prime } + {c^\prime } $ | (3) |
式中:τ为剪切强度;σ为法向应力;f′为摩擦系数;c′为黏聚力。
由式(3)可得,混凝土剪切强度由摩擦力和黏聚力两部分组成。表 2为不同冻融循环次数后混凝土剪切强度的黏聚力和摩擦系数计算结果。从表 2可以看出,摩擦系数整体上随冻融循环次数的增加而降低,但冻融35次后下降得相对较快;黏聚力也随冻融循环次数的增加而降低,但黏聚力降低幅度更大;冻融50次较水饱和状态降幅为59.02%,摩擦系数降幅为13.55%,故可认为混凝土在压剪耦合相关性线性段,黏聚力大幅下降是由于冻融劣化作用起主导作用所致。
| 表 2 不同冻融循环次数下混凝土的黏聚力与摩擦系数 Tab.2 Cohesive stress and friction coefficients of concrete under different freeze-thaw cycles |
Bresler等在八面体应力空间提出了二次抛物线形式的破坏准则[16],其物理表达式如下:
| $ \frac{{{\tau _{{\rm{oct}}}}}}{{{f_{\rm{c}}}}} = a + b\frac{{{\sigma _{{\rm{oct}}}}}}{{{f_{\rm{c}}}}} + c{\left( {\frac{{{\sigma _{{\rm{oct}}}}}}{{{f_{\rm{c}}}}}} \right)^2} $ | (4) |
式中:a,b,c为材料参数;fc为单轴抗压强度;σoct为八面体正应力;τoct为八面体剪应力。其中,八面体正应力σoct和八面体剪应力τoct与主应力σ1,σ2,σ3的转换关系为式(5)和(6)。
| $ {\sigma _{{\rm{oct}}}} = \left( {{\sigma _1} + {\sigma _2} + {\sigma _3}} \right)/3 $ | (5) |
| $ {\tau _{{\rm{oct}}}} = \sqrt {{{\left( {{\sigma _1} - {\sigma _2}} \right)}^2} + {{\left( {{\sigma _2} - {\sigma _3}} \right)}^2} + {{\left( {{\sigma _1} - {\sigma _3}} \right)}^2}} /3 $ | (6) |
试验是平面应力状态下的混凝土压剪破坏,故中间主应力σ2=0,而主应力σ1,σ2,σ3与试验中所获得的正应力和剪应力转换关系为式(7)和(8)。
| $ {\sigma _1} = \frac{\sigma }{2} + \frac{1}{2}\sqrt {{\sigma ^2} + 4{\tau ^2}} $ | (7) |
| $ {\sigma _3} = \frac{\sigma }{2} - \frac{1}{2}\sqrt {{\sigma ^2} + 4{\tau ^2}} $ | (8) |
将式(5)~(8)代入式(4)中,即可得到平面应力状态下混凝土压剪破坏准则表达式,如式(9)所示,但未考虑冻融劣化作用。
| $ \frac{{\sqrt {2{\sigma ^2} + 6{\tau ^2}} }}{{3{f_{\rm{c}}}}} = a + b\frac{\sigma }{{3{f_{\rm{c}}}}} + {\rm{c}}\frac{{{\sigma ^2}}}{{9f_{\rm{c}}^2}} $ | (9) |
采用静态单轴抗压强度fc,单轴抗拉强度ft和剪切强度fv作为3个特征值,将(fc, 0),(ft, 0)和(0, fv)代入式(9)中,即可得到关于参数a,b,c的三元方程,如式(10)所示。
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{\sqrt 2 }}{3} = a + \frac{b}{3} + \frac{c}{9}}\\ {\frac{{\sqrt 2 }}{3}\frac{{{f_{\rm{t}}}}}{{{f_{\rm{c}}}}} = a + \frac{b}{3}\frac{{{f_{\rm{t}}}}}{{{f_{\rm{c}}}}} + \frac{c}{9}\frac{{f_{\rm{t}}^2}}{{f_{\rm{c}}^2}}}\\ {\frac{{\sqrt 6 {f_{\rm{v}}}}}{{3{f_{\rm{c}}}}} = a} \end{array}} \right. $ | (10) |
不同冻融循环次数混凝土单轴抗压强度衰减与冻融循环次数关系可用线性关系式(11)描述[17]。
| $ f_{\rm{c}}^N/f_{\rm{c}}^0 = 1 - {\alpha _{\rm{c}}}N $ | (11) |
式中:fcN为历经N次冻融循环后混凝土单轴抗压强度实测值;fc0为0次冻融循环(水饱和状态)单轴抗压强度实测值;αc为回归系数,表示单轴抗压强度随冻融劣化作用的衰减因子。
混凝土抗拉强度和剪切强度与冻融循环次数的关系表达式参考不同冻融循环次数后混凝土单轴抗压强度衰减与冻融循环次数的线性关系式(11),其表达式分别为式(12)和(13)。
| $ f_{\rm{t}}^N/f_{\rm{t}}^0 = 1 - {\alpha _{\rm{t}}}N $ | (12) |
| $ f_{\rm{v}}^N/f_{\rm{v}}^0 = 1 - {\alpha _{\rm{v}}}N $ | (13) |
式中:ftN(fvN)为历经N次冻融循环后混凝土抗拉(抗剪)强度;ft0 (fv0)为0次冻融循环(水饱和状态)后抗拉(抗剪)强度;αt,αv为回归系数。
根据试验(设计强度C30,边长为300 mm的普通混凝土立方体试件)确定不同冻融循环次数后混凝土抗压强度和抗拉强度(见表 3)。分别利用式(11)~(13)对表 1和表 3中的试验数据进行回归分析,得到回归系数αc=-0.011 09,αt=-0.015 32,αv=-0.017 37,其对应的可决系数R2分别为0.900, 0.900和0.937。
| 表 3 不同冻融循环次数混凝土抗压强度和抗拉强度 Tab.3 Compressive strength and tensile strength of concrete during different freeze-thaw cycle times |
根据平面应力状态下混凝土压剪破坏准则表达式式(9),将式(11)~(13)代入式(9)中,即可得到平面应力状态下考虑冻融劣化作用的混凝土压剪破坏准则表达式,如式(14)所示。
| $ \frac{{\sqrt {2{\sigma ^2} + 6{\tau ^2}} }}{{3f_{\rm{c}}^0\left( {1 - {\alpha _{\rm{c}}}N} \right)}} = a + b\frac{\sigma }{{3f_{\rm{c}}^0\left( {1 - {\alpha _{\rm{c}}}N} \right)}} + c\frac{{{\sigma ^2}}}{{9{{\left[ {f_{\rm{c}}^0\left( {1 - {\alpha _{\rm{c}}}N} \right)} \right]}^2}}} $ | (14) |
将式(11)~(13)代入式(10)中,即可得到关于参数a,b,c的三元方程,如式(15)所示。
| $ \left\{ \begin{array}{l} \frac{{\sqrt 2 }}{3}\frac{{f_t^0\left( {1 - {\alpha _{\rm{t}}}N} \right)}}{{f_{\rm{c}}^0\left( {1 - {\alpha _{\rm{c}}}N} \right)}} = a + \frac{b}{3}\frac{{f_t^0\left( {1 - {\alpha _{\rm{t}}}N} \right)}}{{f_{\rm{c}}^0\left( {1 - {\alpha _{\rm{c}}}N} \right)}} + \frac{c}{9}{\left( {\frac{{f_1^0\left( {1 - {\alpha _1}N} \right)}}{{f_c^0\left( {1 - {\alpha _c}N} \right)}}} \right)^2}\\ \frac{{\sqrt 2 }}{3} = a + \frac{b}{3} + \frac{c}{9}\\ \frac{{\sqrt 6 }}{3}\frac{{f_v^0\left( {1 - {\alpha _v}N} \right)}}{{f_c^0\left( {1 - {\alpha _c}N} \right)}} = a \end{array} \right. $ | (15) |
将表 1和表 3中单轴抗压强度fc、单轴抗拉强度ft和剪切强度fv等3个特征值和回归系数αc,αt,αv的值代入式(15)中,即可求出任一相同冻融劣化作用下参数a,b,c的值(见表 4)。
| 表 4 不同冻融循环次数下模型参数计算结果 Tab.4 Calculation results of model parameters under different freeze-thaw cycle times |
将表 4中不同冻融循环次数下模型参数a, b, c和3.2节中回归系数αc, αt, αv的值分别代入式(14)中,即可得到平面应力状态下不同冻融循环次数后混凝土压剪破坏准则模型,见式(16)~(20)。
| $ 当冻融循环0次时:\tau = 0.408\;24\sqrt {108.186\;29 + 159.850\;64\sigma - 3.574\;48{\sigma ^2}} $ | (16) |
| $ 当冻融循环10次时:\tau = 0.408\;24\sqrt {48.413\;83 + 143.848\;75\sigma - 3.791\;95{\sigma ^2}} $ | (17) |
| $ 当冻融循环25次时:\tau = 0.408\;24\sqrt { - 269.779\;23 + 186.182\;64\sigma - 5.493\;61{\sigma ^2}} $ | (18) |
| $ 当冻融循环35次时:\tau = 0.408\;24\sqrt {12.959\;79 + 117.862\;81\sigma - 4.326\;75{\sigma ^2}} $ | (19) |
| $ 当冻融循环50次时:\tau = 0.408\;24\sqrt {9.876\;2 + 116.278\;63\sigma - 5.897\;85{\sigma ^2}} $ | (20) |
将5种不同冻融循环次数后的混凝土压剪破坏准则曲线方程绘制于图 6中,可见冻融劣化混凝土压剪破坏准则曲线f(σ,τ)与表 2中试验测得的不同冻融循环次数后混凝土在不同法向应力水平下剪切强度数据基本吻合,且在法向应力不超过50%的单轴抗压强度时,混凝土剪切强度随法向应力的提高而增加,与本文试验规律吻合。

|
图 6 不同冻融循环次数的混凝土压剪破坏准则模型与试验数据对比 Fig.6 Comparison between experimental data and compressive-shear failure criterion model of concrete with different freeze-thaw cycle times |
进行了不同冻融循环次数后混凝土在不同法向应力水平下的压剪强度试验,分析了剪切强度、峰值变形及摩擦系数和黏聚力随冻融循环次数和法向应力的变化规律,结论如下:
(1) 当法向应力相同时,随着冻融循环次数的增加,混凝土在各种法向应力状态下的剪切强度均呈逐渐降低趋势,而且法向应力越大,剪切强度随冻融循环次数的增加而降低的程度越小;当冻融循环次数相同且法向应力不大于单轴抗压强度50%时,剪切强度随法向应力的增大而增大,法向应力的存在提高了混凝土的剪切强度。
(2) 在法向应力水平相同时,剪切峰值变形随冻融劣化程度的加深呈正相关性,且法向应力不同,峰值变形与冻融循环次数的关系曲线斜率不同;在冻融循环次数相同时,剪切峰值变形随法向应力的增加而增加。
(3) 摩擦系数和黏聚力与冻融循环次数存在较明显的相关性,二者均随冻融劣化程度的加深而降低。混凝土的剪切强度由摩擦力和黏聚力两部分组成,且随着冻融循环次数的增加,摩擦系数和黏聚力数值均降低,但黏聚力降低幅度更大,故认为混凝土在压剪耦合相关性线性段,黏聚力大幅下降是由于冻融劣化作用起主导作用所致。
(4) 基于八面体应力空间二次抛物线形式破坏准则,转换为用正应力与剪应力表示的压剪破坏准则表达式,建立了考虑冻融循环0~50次作用的混凝土压剪破坏准则,通过与本文试验数据比较,该破坏准则与试验数据吻合相关性较好。
| [1] |
HASAN M, UEDA T, SATO Y. Stress-strain relationship of frost-damaged concrete subjected to fatigue loading[J]. Journal of Materials in Civil Engineering, 2008, 20(1): 37-45. DOI:10.1061/(ASCE)0899-1561(2008)20:1(37) |
| [2] |
PENTTALA V, AL-NESHAWY F. Stress and strain state of concrete during freezing and thawing cycles[J]. Cement and Concrete Research, 2002, 32(9): 1407-1420. DOI:10.1016/S0008-8846(02)00785-8 |
| [3] |
刘博文, 彭刚, 王孝政, 等. 不同冻融循环次数混凝土单轴压缩试验[J]. 水利水运工程学报, 2017(1): 32-36. ( LIU Bowen, PENG Gang, WANG Xiaozheng, et al. Experimental studies on dynamic properties of concrete under different freeze-thaw cycles[J]. Hydro-Science and Engineering, 2017(1): 32-36. (in Chinese)) |
| [4] |
柳琪, 彭刚, 徐童淋, 等. 冻融劣化混凝土循环加卸载外包络线及能量演化[J]. 水利水运工程学报, 2017(6): 85-91. ( LIU Qi, PENG Gang, XU Tonglin, et al. Study of outer envelope curve and energy evolution for freeze-thaw deteriorated concrete under cyclic loading and unloading test[J]. Hydro-Science and Engineering, 2017(6): 85-91. (in Chinese)) |
| [5] |
曹大富, 富立志, 杨忠伟. 冻融循环作用下混凝土的受拉性能研究[J]. 建筑材料学报, 2012, 15(1): 48-52. ( CAO Dafu, FU Lizhi, YANG Zhongwei. Experimental study on tensile properties of concrete after freeze-thaw cycles[J]. Journal of Building Materials, 2012, 15(1): 48-52. DOI:10.3969/j.issn.1007-9629.2012.01.009 (in Chinese)) |
| [6] |
徐童淋, 彭刚, 杨乃鑫, 等. 混凝土冻融劣化后动态单轴抗压特性试验研究[J]. 水利水运工程学报, 2017(6): 69-78. ( XU Tonglin, PENG Gang, YANG Naixin, et al. Experimental studies of dynamic uniaxial compressive properties of concrete after freeze-thaw deterioration[J]. Hydro-Science and Engineering, 2017(6): 69-78. (in Chinese)) |
| [7] |
覃丽坤, 宋玉普, 陈浩然, 等. 双轴拉压混凝土在冻融循环后的力学性能及破坏准则[J]. 岩石力学与工程学报, 2005, 24(10): 1740-1745. ( QIN Likun, SONG Yupu, CHEN Haoran, et al. Mechanical property and failure criterion of concrete under biaxial tension and compression after freeze-thaw cycling[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(10): 1740-1745. DOI:10.3321/j.issn:1000-6915.2005.10.018 (in Chinese)) |
| [8] |
宋玉普, 陈飞, 张众, 等. 冻融环境下引气混凝土双轴拉-压强度和破坏准则的试验研究[J]. 水利学报, 2006, 37(8): 932-937. ( SONG Yupu, CHEN Fei, ZHANG Zhong, et al. Strength reduction of air-entrained concrete under biaxial tension-compression after freeze-thaw cycles and its failure criterion[J]. Journal of Hydraulic Engineering, 2006, 37(8): 932-937. DOI:10.3321/j.issn:0559-9350.2006.08.006 (in Chinese)) |
| [9] |
王立成, 刘汉勇. 海水冻融后轻骨料混凝土的双轴压压强度和变形性能[J]. 水利学报, 2006, 37(2): 189-194. ( WANG Licheng, LIU Hanyong. Strength and deformation characteristics of lightweight aggregate concrete under biaxial compressive stress after freeze-thaw cycling in seawater[J]. Journal of Hydraulic Engineering, 2006, 37(2): 189-194. DOI:10.3321/j.issn:0559-9350.2006.02.010 (in Chinese)) |
| [10] |
宋玉普, 覃丽坤, 张众, 等. 冻融循环后混凝土双轴压的试验研究[J]. 水利学报, 2004(1): 95-99. ( SONG Yupu, QIN Likun, ZHANG Zhong, et al. Experimental study on concrete behavior under biaxial compression after freezing and thawing cycle[J]. Journal of Hydraulic Engineering, 2004(1): 95-99. DOI:10.3321/j.issn:0559-9350.2004.01.018 (in Chinese)) |
| [11] |
田威, 张鹏坤, 谢永利, 等. 冻融环境下基于CT技术混凝土孔隙结构的三维分布特征[J]. 长安大学学报(自然科学版), 2016(3): 49-55. ( TIAN Wei, ZHANG Pengkun, XIE Yongli, et al. 3D distribution characteristics on concrete porous structure under freeze-thaw environment based on CT technique[J]. Journal of Chang'an University(Natural Science Edition), 2016(3): 49-55. DOI:10.3969/j.issn.1671-8879.2016.03.008 (in Chinese)) |
| [12] |
宾峰.冻融循环作用下岩石动态力学特性及微观机理研究[D].长沙: 中南大学, 2014. (BIN Feng. Study on dynamic mechanical properties and microstructure mechanism of rock under freeze-thaw cycles[D]. Changsha: Central South University, 2014. (in Chinese)) http://cdmd.cnki.com.cn/Article/CDMD-10533-1014398695.htm
|
| [13] |
RYSHKEWITCH E. Compression strength of porous sintered alumina and zirconia[J]. Journal of the American Ceramic Society, 2010, 36(2): 65-68. |
| [14] |
闻伟.碾压混凝土单轴动态和压剪静态性能试验研究[D].大连: 大连理工大学, 2012. (WEN Wei. Experimental research on properties of RCC under uniaxial dynamic and compression-shear static stress state[D]. Dalian: Dalian University of Technology, 2012. (in Chinese)) http://cdmd.cnki.com.cn/Article/CDMD-10141-1012394452.htm
|
| [15] |
宋玉普, 闻伟, 王怀亮. 碾压混凝土压剪强度分析[J]. 水利与建筑工程学报, 2012, 10(6): 44-47. ( SONG Yupu, WEN Wei, WANG Huailiang. Analysis on compression-shear strength of roller compacted concrete[J]. Journal of Water Resources and Architectural Engineering, 2012, 10(6): 44-47. DOI:10.3969/j.issn.1672-1144.2012.06.011 (in Chinese)) |
| [16] |
BRESLER B, PISTER K S. Strength of concrete under combined stresses[J]. ACI Structural Journal, 1958, 1(1): 41-56. |
| [17] |
商怀帅, 宋玉普, 覃丽坤. 普通混凝土冻融循环后性能的试验研究[J]. 混凝土与水泥制品, 2005(2): 9-11. ( SHANG Huaishuai, SONG Yupu, QIN Likun. Experimental study on the performance of ordinary concrete after freeze-thaw cycle[J]. China Concrete and Cement Products, 2005(2): 9-11. DOI:10.3969/j.issn.1000-4637.2005.02.003 (in Chinese)) |
2. Hubei Key Laboratory of Disaster Prevention and Mitigation (China Three Gorges University), Yichang 443002, China
 2019
2019 
