目前,混凝土材料仍是基础设施建设领域应用最广泛的材料,并且随着时代的发展,各种复杂的结构体还将不断涌现。因此,只有更加深入研究混凝土损伤演化,才能给混凝土结构的整体安全性分析提供理论基础。Dougill[1]最早发现损伤力学与混凝土非线性特性的关系极为紧密; 继他之后,对混凝土损伤特性的研究就越来越多。Mazars[2]首次采用应力张量分解法,并假设由正应力引起受压损伤,负应力引起受拉损伤;Ananiev等[3]基于混凝土加载过程存在塑性变形这一特性,建立了混凝土塑性损伤模型;Jason等[4]建立了结合塑性应变和损伤演化的弹塑性损伤模型;Oliver等[5]将混凝土加载过程中拉、压应力的区分,通过拉压应力分量的退化来定义混凝土的损伤变量;王春来等[6]针对混凝土在单调荷载条件下损伤行为的复杂性,根据Weibull统计分布理论和等效应变假定原理,得出了混凝土损伤本构的经验公式;在王春来等[6]研究的基础上,王乾峰[7]提出了峰前基于Weibull统计理论,峰后基于Longnormal统计理论的分段式本构方程,且大量试验证明,该本构方程的拟合效果较好;杜成斌等[8]所构建的混凝土损伤模型考虑了应变软化,结果证明,随着应变率增加,混凝土的破坏形式明显由单条宏观裂缝向多条裂纹变化;马怀发等[9]提出了一种适用于复杂应力状态下的双折线弹性损伤模型,该模型考虑了混凝土的速率效应;Haussler-Combe等[10]基于黏弹性观点,考虑到高加载速率下混凝土的惯性效应,提出了相应的损伤本构模型。马小亮等[11]将混凝土的损伤演化划分为损伤初始发展阶段、损伤快速发展阶段和完全破坏阶段3个阶段,并分析了加载速率对损伤转折点的影响;胡海蛟等[12]研究了混凝土在不同加载速率下损伤特性。
综上所述,目前关于混凝土静态单轴受拉、受压损伤机理的认识已经越来越清晰,然而有关混凝土在复杂应力状态下的损伤机理研究则较少。因此本文开展了对常态混凝土进行5种侧压(0,0.12fc,0.24fc,0.36fc,0.48fc)和5种应变速率(10-5/s,5×10-5/s,10-4/s,5×10-4/s,10-3/s)的双轴动态压缩试验分析研究。
1 试验设计试验采用三峡大学的TAZW-10000型10 MN大型多功能液压伺服动静力三轴仪。该系统由油压系统、加载系统和围压系统组成,通过EDC控制器实时控制3个加载方向,实现静动态循环加卸载试验。
试验采用的混凝土试件按C30的设计强度进行配合比设计,水泥采用P·O 42.5普通硅酸盐水泥,选用中砂,碎石粒径为5~40 mm, 其中小石粒径5~20 mm, 中石粒径20~40 mm,试件采用300 mm的立方体,待试件浇筑完成,拆模后将试件放入标准养护室养护。混凝土各配料用量为:水175.0 kg/m3, 水泥291.0 kg/m3, 砂676.9 kg/m3, 小石502.8 kg/m3, 中石754.3 kg/m3。
力学试验步骤如下:①装样及对中:将试件置于夹具内,放置于试验机下并严格对中;②变形计安装:安装变形计至试件周边并用仪器检验其传导正常;③预加载:利用移动和移动转换指令分别使试件竖向、侧向预加载至20 kN;④侧向加载:采用负荷控制方式(2 000 N/s)加载侧压至拟定大小(0,0.12fc,0.24fc,0.36fc,0.48fc);⑤竖向加载:利用移动转换命令中的变形控制方式进行操作,按预定加载速率(10-5/s,5×10-5/s,10-4/s,5×10-4/s和10-3/s)加载,直至到试件破坏;⑥试验完成,保存采集到的负荷-变形曲线数据。
2 应力应变全曲线分析将试验采集到的负荷-变形全曲线数据,整理得到应力、应变数据绘制出应力-应变曲线如图 1和2所示。
|
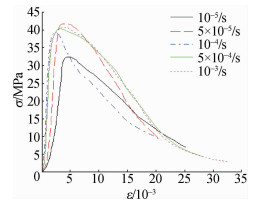
图 1 混凝土动态单轴受压应力-应变曲线 Fig.1 Dynamic uniaxial compression stress-strain curves of concrete |
|
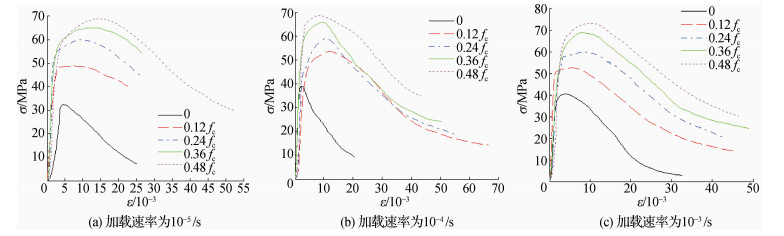
图 2 不同加载速率下的双轴受压应力-应变曲线 Fig.2 Stress-strain curves of biaxial compression under different loading rates |
结合图 1和图 2可得:①曲线上升段的走势为曲线上升-直线上升-曲线上升至峰值点,并且加载速率越大,压密阶段越短,曲线上升越快,峰值应力也越大。②相同加载速率下,峰值应力随侧压力增大而增大;③加载速率相同时,不同侧压下混凝土应力-应变曲线下降趋势基本一致,即混凝土达到峰值应力后承载力下降趋势不受侧压影响。
3 基于Najar能量法的损伤演化分析 3.1 基于能量角度的损伤变量定义混凝土是一种弹塑性损伤材料,其损伤和塑性变形、变形模量的退化是同步发生的[12-13]。罗曦等[14]对Najar能量法进行了改进。
| $ D = \frac{{{W_{\rm{D}}}}}{{{W_{{\rm{pef}}}}}} = 1 - \frac{{{E_{\rm{r}}}}}{{{E_0}}}{\left( {\frac{{{\varepsilon _{\rm{e}}}}}{\varepsilon }} \right)^2} $ | (1) |
式中:D为损伤变量; WD为耗散能; Wperf为无损材料的应变能; E0为混凝土初始弹性模量;Er为混凝土任意点卸载后再加载的变形模量;ε为任一点的应变;εe为任意一点的弹性应变。
从式(1)可见,Er/E0反映了加载过程中混凝土刚度的退化,而εe/ε则反映了混凝土在加载过程中弹性应变与总应变比值的变化规律,因此这种损伤变量定义具有明确的物理意义。
3.2 损伤演化表达式的定义 3.2.1 双轴受压状态下混凝土刚度的退化关于混凝土受载过程中刚度退化的演变过程,目前很多是基于应力-应变空间的经验公式[7, 15],丁发兴等[16]从能量法角度推导出了混凝土的刚度退化与应变能的关系,其表达式具有通用性,适用于双轴受压的情况。表达式为:
| $ \frac{{{E_{\rm{r}}}}}{{{E_0}}} = \frac{\sigma }{{\sqrt {2{E_0}{W_{{\rm{P}} + {\rm{E}}}}} }} $ | (2) |
式中:E0取应力-应变曲线中峰值应力40%~50%时的割线斜率;WP+E为混凝土的弹塑性应变能,采用微分近似算法,其示意图如图 3所示。

|
图 3 Najar能量损伤示意 Fig.3 Najar energy damage diagram |
| $ {W_{{\rm{P}} + {\rm{E}}}} = \int_0^\sigma \sigma {\rm{d}}\varepsilon \approx \sum\limits_{\xi = 1}^i {\frac{{{\sigma _\xi } + {\sigma _{\xi - 1}}}}{2}} \left( {{\varepsilon _\xi } - {\varepsilon _{\xi - 1}}} \right) $ | (3) |
式中:σξ-1和σξ分别为某一微分段前后的应力;εξ-1和εξ分别为微分段前后的应变。所有工况下,计算WP+E的微分段数均在2 000段以上。
由整理得到的应力-应变曲线包络线以及其应力、应变数据,经式(2)与(3)可以得到混凝土在不同侧压大小下和不同应变速率下的刚度退化过程。以应变速率10-4/s时的单轴受压数据为例,应力-应变曲线与刚度退化过程的对比见图 4,其中应力为归一化后的数据。

|
图 4 单轴受压刚度退化 Fig.4 Uniaxial compression stiffness degradation curves of concrete |
分析图 4可以看出混凝土刚度退化曲线是先增后减,因为试验所用试件的材料内部难以避免地存在一些天然的微裂纹和微孔隙,这些微裂纹和微孔隙在加载初期会先变小,使得混凝土材料“由松变紧”,刚度逐渐增大。宏观表现就是混凝土加载初期有一个压密阶段。这一点反映在应力-应变曲线上就是加载初期有一个略凹的阶段。因此,试验数据呈现出来的结果为加载初期,混凝土的刚度增大,应力-应变曲线由凹变凸。压密阶段结束后继续加载,混凝土产生新的裂纹和孔隙并逐渐扩展至相互贯穿,混凝土“由紧变裂”,刚度逐渐减小,并且开始减小时对应的应变大致与应力-应变曲线直线上升段结束时的应变相同。
为能更好地符合损伤力学的基本观点,忽略试件加载初期刚度增大过程,近似地认为该过程中混凝土的刚度不发生改变,即假设混凝土在加载初期处于线弹性阶段。对图 4中的混凝土刚度退化过程进行修正,将图 4中刚度退化曲线的上升段改为平直段。后面关于刚度退化的分析均以这种方法修正。
3.2.2 加载速率对刚度退化的影响混凝土在加载速率为10-5/s,5×10-5/s,10-4/s,5×10-4/s和10-3/s时单轴加载过程中的刚度退化曲线如图 5所示,其曲线也是按照前文所述方法将曲线上升段改为平直段。

|
图 5 不同加载速率下单轴受压的刚度退化曲线 Fig.5 Stiffness degradation curves of concrete under different loading rates |
由图 5可见:改进后的刚度退化过程可以分为3个阶段,①刚度不变阶段,即材料的线弹性阶段;②刚度加速退化阶段。在此阶段中,刚度退化的速度不断加大,对应曲线呈下凹状;③刚度平稳变化阶段。该阶段刚度变化的速度逐渐变小,最终趋于稳定。加载速率越大,材料的线弹性阶段越短,刚度加速退化阶段对应的应变范围越小。刚度退化随着加载速率的减小出现一定滞后现象,这种规律并不严格满足,总体上表现出加载速率越大,刚度退化越明显的规律。
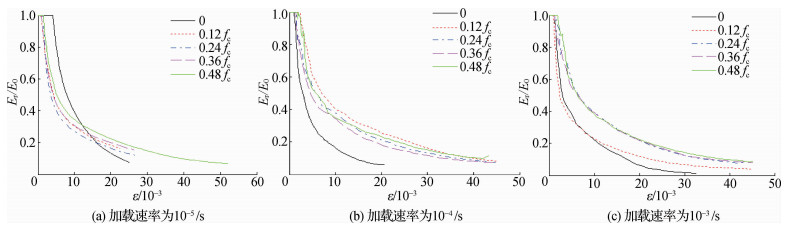
3.2.3 侧压对刚度退化的影响混凝土在不同加载速率(10-5/s,10-4/s,10-3/s)和不同侧压下的刚度退化曲线如图 6所示。其曲线也是按照前文所述方法将曲线上升段改为平直段。
|
图 6 不同侧压下双轴受压刚度退化曲线 Fig.6 Stiffness degradation curves of concrete under different lateral pressures |
由图 6可得:①相同加载速率下,侧应力越大,刚度不变阶段越长,即混凝土线弹性阶段越长;②加载速率较低时,侧压对刚度快速减小阶段的影响不明显;③加载速率较高时,侧压稍大的刚度退化相对较缓。④加载速率相同时,刚度退化随着侧应力的增加而出现明显的滞后。
依据上述结论进而分析得到,侧应力对混凝土的压实作用使其提前进入弹性变形阶段,同时又约束了混凝土的横向变形。初期使混凝土线弹性阶段的应变范围变大,侧应力越大,约束程度越高,对混凝土刚度退化的减缓程度也就越高。
3.3 基于能量角度的损伤演化分析 3.3.1 损伤演化分析结合本文工况,在已知加载过程中每一点的刚度后,即可通过式(4)求得该点理论上的弹性应变和塑性应变。
| $ \left\{ {\begin{array}{*{20}{l}} {{\varepsilon _{\rm{e}}} = \frac{\sigma }{{{E_{\rm{r}}}}}}\\ {{\varepsilon _{\rm{p}}} = \varepsilon - {\varepsilon _{\rm{e}}}} \end{array}} \right. $ | (4) |
式中:σ为任意点的轴向应力;εe,εp和ε分别为任意点的弹性应变、塑性应变和总应变;Er为任意点的变形模量。
将式(4)代入式(1)可得到基于理论推导的混凝土损伤演化表达式:
| $ D = 1 - \frac{{{E_{\rm{r}}}}}{{{E_0}}}{\left( {\frac{{{\varepsilon _{\rm{e}}}}}{\varepsilon }} \right)^2} = 1 - \frac{{{\sigma ^2}}}{{{E_{\rm{r}}}{E_0}{\varepsilon ^2}}} $ | (5) |
由式(5)可以计算出任意点损伤变量。以应变速率10-4/s时的单轴受压数据为例,应力-应变曲线与损伤演化曲线的对比如图 7所示,其中应力为归一化后的数据。

|
图 7 单轴受压损伤演化 Fig.7 Uniaxial compression damage evolution of concrete |
从图 7可见,明显损伤演化曲线是先减后增的变化规律而并非从0开始增大,这一点明显与损伤力学基本观点不相符。而在上一节中对基于理论推导的混凝土刚度退化曲线进行了修正,确定了混凝土加载过程中的线弹性阶段。因此只对刚度退化进行了修正,而没有对应力-应变曲线的压密段进行适当修正,导致计算的损伤演化曲线如图 7所示,加载初期出现了明显的下降段。整个曲线呈明显的先减后增趋势,与损伤理论建议的损伤演化趋势有所不同。混凝土损伤演化曲线的下降段对应应力-应变曲线的混凝土压密段。产生这种现象的原因与上一节刚度退化出现上升段的原因相同。
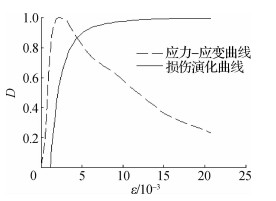
因此,需要进行适当的修正,即认为压密阶段由加载带来的损伤几乎为零,即曲线下降段改为平直段,计算压密段过后的损伤时采用的总应变应当减去压密阶段的塑性应变。图 8为修正后的损伤演化曲线与应力-应变曲线的对比图。后面关于损伤演化曲线的分析均以这种方法修正。
|
图 8 修正后的单轴受压损伤演化 Fig.8 Corrected uniaxial compression damage evolution of concrete |
从图 8的损伤演化曲线形状可以看出,损伤变量大体上呈“S”型发展,这与Weibull损伤模型有相似之处[7],损伤演化可以分为3个阶段:
(1) 线弹性阶段。该阶段混凝土材料为线弹性,外界输入的能量全部转化为弹性能,无损伤耗散能的产生,损伤变量为0。
(2) 损伤加速发展阶段。该阶段损伤耗散能占理论输入总能量的比例越来越大,即混凝土转化弹性能的能力越来越弱,最终混凝土发生破坏。表现为损伤变量迅速增大,并在混凝土达到极限抗压强度后,损伤变量增长至0.8左右。
(3) 损伤收敛阶段。该阶段混凝土应力-应变趋于平稳,损伤变量平稳趋近于1。从损伤发展的程度来说,由于损伤变量是定义在[0, 1]之间的变量,其最终必定是收敛于1的,而在损伤变量开始无限趋近于1时,也近似为应力-应变曲线开始平稳变化的收敛点。
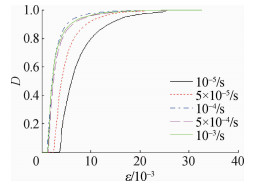
3.3.2 应变速率对损伤演化的影响按照上述损伤演化的修正方式,混凝土在加载速率10-5/s,5×10-5/s,10-4/s,5×10-4和10-3/s时单轴加载过程中的损伤演化曲线见图 9。
|
图 9 不同应变速率下单轴受压的损伤演化曲线 Fig.9 Damage evolution curves of uniaxial compression under different loading rates |
从图 9可以发现,应变速率越大,材料的线弹性阶段越短,损伤加速发展阶段的损伤变量的增长越迅速且该阶段对应的应变范围越小。进而分析得出,加载速率影响混凝土的能量释放形式。混凝土在静态加载时,其损伤发展遵循“最小吸能原理”,整个过程能量释放相对比较平稳。而混凝土在动态加载时,随着应变速率越高,混凝土越易于发生脆性破坏,并且能量释放集中且快速。
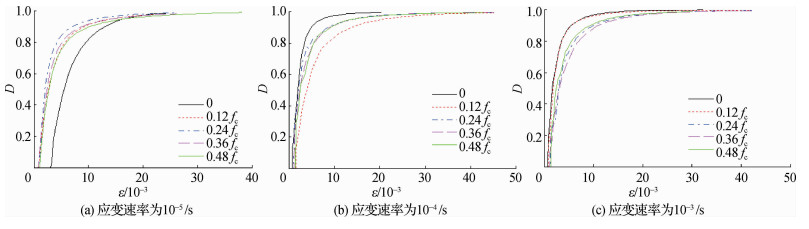
3.3.3 侧压大小对损伤演化的影响图 10为应变速率10-5/s,10-4/s,10-3/s时,在不同侧压下的混凝土双轴受压损伤演化曲线。
|
图 10 不同侧压下双轴受压损伤演化曲线 Fig.10 Biaxial compression damage evolution curves under different lateral pressures |
由图 10可知,加载速率相同时,混凝土损伤的发展随着侧应力的增大而出现滞后现象,侧应力越小,同一应变速率下混凝土的损伤发展速度越快。说明侧应力的存在阻碍了损伤的发展,且侧应力越大,对混凝土损伤发展的阻碍作用也越大。
混凝土在双轴受压应力状态下,侧应力作用的方向正好抑制了竖向压应力作用产生的竖向裂纹的发展,从而使混凝土较没有侧应力的情况更密实,混凝土积聚弹性应变能的能力越强,也就在一定程度上阻止了混凝土的损伤发展。而侧应力越大,对裂缝发展的阻碍作用越强,混凝土损伤发展的滞后性越明显。
4 结语试验中得到的负荷-变形曲线包括上升段以及下降段,研究更符合实际。另外比较了混凝土在不同加载速率和不同侧压大小下的动态压缩特性。基于原Najar能量法提出了一种新的损伤变量计算方法,选取合适的刚度退化计算式,探究了加载速率及侧压对其影响。根据损伤演化的具体过程,可将混凝土的损伤演化分为线弹性、损伤加速变化和损伤收敛3个阶段。侧应力对混凝土的损伤演化影响明显。随着侧应力的增大,混凝土刚度退化明显变慢,最终表现为侧应力的增大延缓了混凝土的损伤发展速度。加载速率对混凝土损伤演化的影响也具有一定规律性,加载速率越快,混凝土损伤演化越快。
| [1] |
DOUGILL J W. On stable progressively fracturing solids[J]. Zeitschrift Für Angewandte Mathematik Und Physik Zamp, 1976, 27(4): 423-437. DOI:10.1007/BF01594899 |
| [2] |
MAZARS J. A description of microscale and macroscale damage of concrete structures[J]. Engineering Fracture Mechanics, 1986, 25(5/6): 729-737. |
| [3] |
ANANIEV S, OZBOLT J. Plastic-damage model for concrete in principal directions[J]. Condensed Matter, 2007. |
| [4] |
JASON L, HUERTA A, PIJAUDIER-CABOT G, et al. An elastic plastic damage formulation for concrete: application to elementary tests and comparison with an isotropic damage model[J]. Computer Methods in Applied Mechanics and Engineering, 2006, 195(52): 7077-7092. DOI:10.1016/j.cma.2005.04.017 |
| [5] |
OLIVER J, RUI F, CERVERA M. Modeling material failure in concrete structures under cyclic actions[J]. Journal of Structural Engineering, 2004, 130(12): 1997-2005. DOI:10.1061/(ASCE)0733-9445(2004)130:12(1997) |
| [6] |
王春来, 徐必根, 李庶林, 等. 单轴受压状态下钢纤维混凝土损伤本构模型研究[J]. 岩土力学, 2006, 27(1): 151-154. ( WANG Chunlai, XU Bigen, LI Shulin, et al. Study on a constitutive model of damage of SFRC under uniaxial compression[J]. Rock and Soil Mechanics, 2006, 27(1): 151-154. DOI:10.3969/j.issn.1000-7598.2006.01.030 (in Chinese)) |
| [7] |
王乾峰.钢纤维混凝土动态损伤特性研究[D].宜昌: 三峡大学, 2009. (WANG Qianfeng. Dynamic damage characteristics of steel fiber reinforced concrete[D]. Yichang: China Three Gorges University, 2009. (in Chinese))
|
| [8] |
杜成斌, 江守燕, 徐海荣, 等. 湿筛混凝土试件的静、动破坏数值模拟[J]. 河海大学学报(自然科学版), 2012, 40(2): 195-200. ( DU Chengbin, JIANG Shouyan, XU Hairong, et al. Numerical simulation of static and dynamic failure of wet-screened concrete specimens[J]. Journal of Hohai University(Natural Sciences), 2012, 40(2): 195-200. DOI:10.3876/j.issn.1000-1980.2012.02.013 (in Chinese)) |
| [9] |
马怀发, 陈厚群, 阳昌陆. 复杂动荷载作用下全级配混凝土损伤机理细观数值试验[J]. 土木工程学报, 2012, 45(7): 175-182. ( MA Huaifa, CHEN Houqun, YANG Changlu. Numerical test of micro-scale damage mechanism for full graded concrete under complicated dynamic loads[J]. Journal of Civil Engineering, 2012, 45(7): 175-182. (in Chinese)) |
| [10] |
HÄUSSLER-COMBE U, KVHN T. Modeling of strain rate effects for concrete with viscoelasticity and retarded damage[J]. International Journal of Impact Engineering, 2012, 50: 17-28. DOI:10.1016/j.ijimpeng.2012.08.002 |
| [11] |
马小亮, 彭刚, 肖杰, 等. 不同加载速率下混凝土损伤阶段的划分[J]. 水利水运工程学报, 2016(6): 90-96. ( MA Xiaoliang, PENG Gang, XIAO Jie, et al. Damage stage division of concrete under different loading rates[J]. Hydro-Science and Engineering, 2016(6): 90-96. (in Chinese)) |
| [12] |
胡海蛟, 彭刚, 谢玖杨, 等. 混凝土循环加卸载动态损伤特性研究[J]. 工程力学, 2015, 32(6): 141-145. ( HU Haijiao, PENG Gang, XIE Jiuyang, et al. Study on dynamic behaviour of concrete by cycle loading and unloading conditions[J]. Engineering Mechanics, 2015, 32(6): 141-145. (in Chinese)) |
| [13] |
殷有泉. 岩石的塑性、损伤及其本构表述[J]. 地质科学, 1995, 30(1): 63-70. ( YIN Youquan. On rock plasticity, damage and their constitutive formulation[J]. Geoscience, 1995, 30(1): 63-70. (in Chinese)) |
| [14] |
罗曦, 彭刚, 刘博文, 等. 用改进Najar能量法分析混凝土单轴受压损伤特性[J]. 水利水运工程学报, 2016(5): 103-108. ( LUO Xi, PENG Gang, LIU Bowen, et al. Analysis of damage characteristics of concrete under uniaxial compression by improved Najar energy method[J]. Hydro-Science and Engineering, 2016(5): 103-108. (in Chinese)) |
| [15] |
吴科如. 混凝土在压力荷载下弹性变形和残余变形的变化及其脆性系数[J]. 同济大学学报(自然科学版), 1983(1): 72-85. ( WU Keru. The elastic and permanent deformation fractions of concrete under uniaxial compression and its factor[J]. Journal of Tongji University(Natural Science), 1983(1): 72-85. (in Chinese)) |
| [16] |
丁发兴, 余志武, 欧进萍. 混凝土单轴受力损伤本构模型[J]. 长安大学学报(自然科学版), 2008, 28(4): 70-73. ( DING Faxing, YU Zhiwu, OU Jinping. Uniaxial damage constitutive model of concrete[J]. Journal of Chang'an University(Natural Science Edition), 2008, 28(4): 70-73. DOI:10.3321/j.issn:1671-8879.2008.04.016 (in Chinese)) |
 2019
2019 
