渡槽是跨越河谷、洼地、道路等地形的空间薄壁输水建筑物,被广泛应用于农业灌溉工程和其他大型水利工程中。其结构与水接触面积大,输水过程具有间断性和水位变化等特点。由于受到间断性和水位变幅的影响,渡槽内部湿度呈非均匀变化[1-2],引起不均匀的湿胀和干缩变形,使结构内应力发生变化,从而对结构产生不利影响,甚至造成结构破坏。所以,湿度对渡槽槽身的影响更直接关乎结构的安全稳定性。
黄海东等研究了变湿环境下混凝土桥梁的长期收缩变形、结构干缩自应力分布规律及时变特征[3]。樊明哲等通过实测数据得到湿度对大坝应力变形的影响[4-5]。周耀等开展5根钢筋混凝土简支梁浸泡后的动力性能试验,采用有限元法分析了湿度对简支梁动力性能的影响[6]。以上研究均针对杆件或实体结构,但对于路面板、水闸及渡槽等薄壁结构来说,其比表面积要比大坝等大体积混凝土大得多,因此水分扩散相对快且大,湿度变形也更为突出。而此方面研究成果较少。魏亚提出了混凝土路面板湿度梯度形成机理,结合湿度与变形的本构关系,建立了混凝土路面湿度翘曲及应力计算方法[7];在此基础上,高翔等研究了湿度与荷载耦合对路面板翘曲变形和应力的影响[8]。马跃先等通过建立湿度场与应力场数学模型采用有限元法研究了湿度对水闸结构的影响[9]。湿度不仅引起混凝土薄壁结构湿胀变形[10],而且影响混凝土弹性模量[11-13],以上研究表明湿度对薄壁结构影响较大,但并未考虑到混凝土材料性能受湿度影响,使得混凝土构件力学性能发生变化[14-16]。
弹性模量是混凝土材料最重要的力学性能之一,它反映了混凝土所受应力和所产生应变之间的关系;湿胀变形是混凝土内部湿度变化的结果,了解混凝土湿度特性及湿度场分布规律是弄清混凝土湿胀变形机理的前提和基础,精确计算湿胀应变值则是防止结构破坏的关键。因此考虑弹性模量和湿胀综合效应分析研究混凝土湿度场与应力场之间的相互关系对于实际工程设计具有指导意义。本文以渡槽为例,基于湿度扩散理论采用大型商业软件COMSOL Multiphysics进行有限元仿真计算,揭示湿度沿槽壁的分布及其作用下渡槽的应力变形规律,为今后渡槽的设计和防渗提供理论支撑。
1 混凝土构件湿度和变形计算理论 1.1 混凝土湿度计算模型路面板、渡槽等混凝土构件具有与外部环境接触面积大的特点,因此受环境影响较为显著。尤其是在构件表面与水长时间接触后,水分会缓慢迁移,在构件内形成一定湿度分布。因此,采用Fick第二定律的湿度扩散方程描述水分扩散的湿度梯度分布,其方程为[9]:
| $ \frac{{\partial h}}{{\partial t}} = \frac{\partial }{{\partial x}}\left( {D(h)\frac{{\partial h}}{{\partial x}}} \right) $ | (1) |
| $ D(h) = {D_0}\left\{ {{a_0} + \frac{{1 - {a_0}}}{{1 + {{\left[ {(1 - h)/\left( {1 - {h_{\rm{c}}}} \right)} \right]}^n}}}} \right\} $ | (2) |
式中:h为混凝土相对湿度;t为时间(s);x为传输方向上的空间位置(m);D(h)是以混凝土相对湿度h为变量的扩散系数(m2/s),采用Bazant等[17]的三参数扩散系数方程来计算;D0为饱和混凝土的湿度扩散系数(m2/s);n为湿度非线性扩散方程的回归系数,表示D(h)的下降速率,通常取6~16;hc为扩散系数曲线拐点的相对湿度;a0为经验系数,Kim等[18]建议取a0=0.05,hc=0.8。
为了确定混凝土构件水分扩散系数及验证模型的合理性,进行混凝土一维吸水试验来反演得到扩散系数, 详见文献[19]。得到C30混凝土的模型参数为D0=1.254×10-8 m2/s,a0=0.05,n=6,hc=0.8。
根据反演得到的湿度扩散系数,有限元模拟分析的吸水曲线和试验测得的吸水曲线基本吻合,验证了基于Fick第二定律建立的混凝土一维自由吸水模型的合理性。
1.2 考虑湿度影响的混凝土弹性本构方程对于平面应力问题,考虑湿度对弹性模量影响和湿胀作用的混凝土材料本构方程为:
| $ \left\{ {\begin{array}{*{20}{l}} {{\varepsilon _x} = \frac{1}{{E(w)}}\left[ {{\sigma _x} - \mu \left( {{\sigma _y} + {\sigma _z}} \right)} \right] + {\alpha _{\rm w}}\Delta w}\\ {{\varepsilon _y} = \frac{1}{{E(w)}}\left[ {{\sigma _y} - \mu \left( {{\sigma _z} + {\sigma _x}} \right)} \right] + {\alpha _{\rm w}}\Delta w}\\ {{\varepsilon _z} = \frac{1}{{E(w)}}\left[ {{\sigma _z} - \mu \left( {{\sigma _x} + {\sigma _y}} \right)} \right] + {\alpha _{\rm w}}\Delta w}\\ {{\gamma _{xy}} = \frac{{2(1 + \mu )}}{{E(w)}}{\tau _{xy}};{\gamma _{yz}} = \frac{{2(1 + \mu )}}{{E(w)}}{\tau _{yz}};{\gamma _{zx}} = \frac{{2(1 + \mu )}}{{E(w)}}{\tau _z}} \end{array}} \right. $ | (3) |
式中:E(w)为混凝土弹性模量(GPa);w为混凝土内部含水率; μ为泊松比; σx,σy,σz,τxy,τyz,τzx为应力;εx,εy,εz,γxy,γyz,γzx为应变;Δw为含水率变化;αw为湿胀系数,混凝土湿胀系数为3.24×10-3~3.58×10-3 [6],采用3.25×10-3。
依据试验结果[20]可得弹性模量随湿度变化表达式为:
| $ E(w) = 24.31 + 130w $ | (4) |
采用修正后的BET模型将湿度h转化为含水率w:
| $ w = \frac{{C{W_{{\rm{uni}}}}h}}{{1 + (C - 1)h}}\left[ {\frac{{1 - {h^Q}}}{{1 - h}} + \frac{{{h^{QP}}}}{{1 - {h^P}}}\left( {1 - {h^{PM}}} \right)} \right] $ | (5) |
式中: Wuni=0.009是吸附于水化产物表面的单一水分子层的质量;C=6.669是热性能参数;Q,P,M由混凝土试件等温吸附-脱附曲线得到,分别为4.875,0.348和1.08[8]。
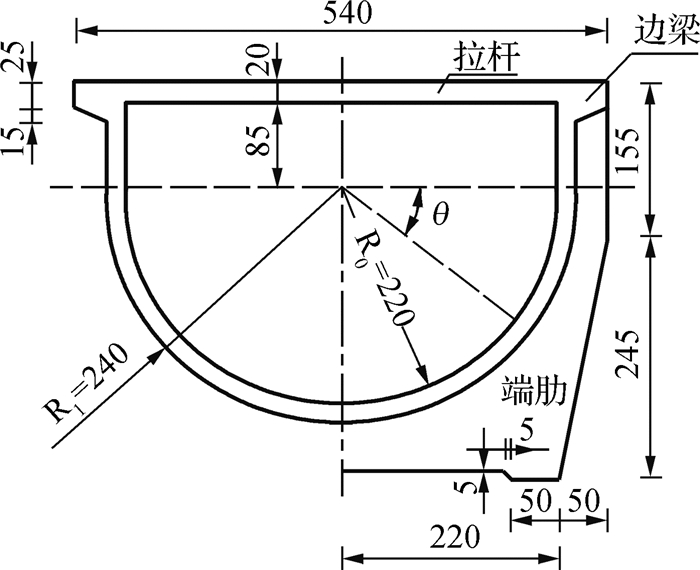
2 湿度对混凝土渡槽结构受力变形影响 2.1 渡槽基本参数槽身长10 m,设置5根拉杆,拉杆间距2.45 m,两端简支。渡槽断面如图 1所示,槽壳内半径R0=2.2 m,槽壳壁厚0.2 m,外半径Rl=2.4 m,直段高f=0.95 m(圆心到拉杆中心距离),槽壳顶部加厚形成边梁。槽身两端设有端肋,端肋厚0.3 m。槽身采用C30混凝土浇筑,混凝土干燥弹性模量Ec=24.31 GPa。槽内水深H=3.0 m。考虑的外荷载有:渡槽槽身及端肋自重、槽内水重、人行桥传至边梁的荷载(包括人群荷载及桥面板重)为4.704 kN/m。
|
图 1 渡槽断面(单位:mm) Fig.1 Aqueduct profile (unit: mm) |
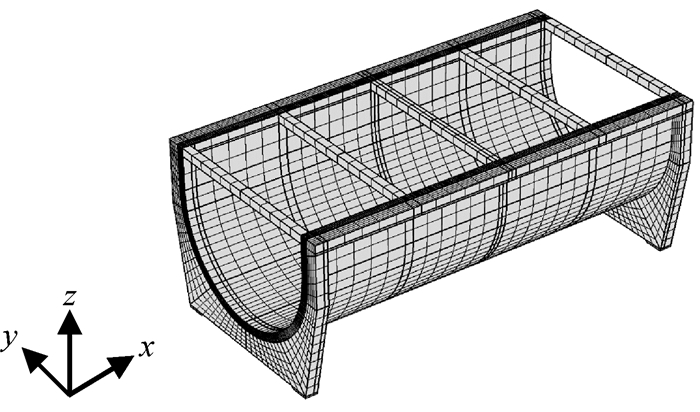
取单跨度左侧端肋处渡槽圆弧段圆心为坐标原点,y轴为垂直水流方向,向左为正;z轴为铅垂方向,向上为正;x轴为顺水流方向,符合右手螺旋准则。U型渡槽属于空间薄壁结构,在数值模型中采用六面体8节点三维实体单元进行剖分。为了保证计算精度,沿渡槽槽身厚度方向划分了10层网格,最大单元尺寸为0.432 m,最小单元尺寸为0.020 m,整个渡槽共剖分17 248个单元,151 478个节点,渡槽网格剖分如图 2所示。
|
图 2 渡槽网格划分 Fig.2 Aqueduct meshing |
受力变形分析模型中,槽底4处支座分别施加XYZ约束、XY约束、Y约束及YZ约束。在湿度场模型中,混凝土水分扩散系数按式(1)计算。混凝土材料的干燥弹性模量为24.31 GPa,不同湿度下弹性模量按式(4)计算。泊松比认为不受湿度影响,取0.167。假设渡槽混凝土为线弹性材料,控制方程(1)中渡槽初始条件为:渡槽内部相对湿度为0.4;边界条件为:槽壁内侧湿度采用第一类边界条件相对湿度1.0,槽壁外侧不存在湿交换和变化,采用∂h/∂x=0和相对湿度为0.4的边界条件。
2.3 求解过程应用Comsol Multiphysics软件对混凝土渡槽进行数值模拟。空间域采用有限元法进行离散,时间域采用有限差分法离散,总步长为10 d,最大步长和初始步长分别设置为0.1 d和0.001 d。
分析中不考虑湿度场与应力场的耦合,首先按照式(1)微分方程求解瞬态湿度场,得到不同时刻渡槽内湿度分布。在湿度求解中,采用迭代法考虑湿度扩散系数随湿度的变化规律。得到每一时刻湿度场分布后,利用式(4)计算弹性模量,进行渡槽弹性分析,得到位移、应变及应力等分布。为分析湿度作用下渡槽主要断面的内力图,取跨中及端肋处横断面,进一步由应力分布计算出沿径向的各断面弯矩及轴力,具体计算过程如下[21]:
(1) 任意θ断面极坐标系下应力分量与整体坐标下的应力分量转化式为:
| $ \left\{ {\begin{array}{*{20}{l}} {{\sigma _r}}\\ {{\sigma _\theta }}\\ {{\tau _{r\theta }}} \end{array}} \right\} = \left[ {\begin{array}{*{20}{c}} {{{\cos }^2}\theta }&{{{\sin }^2}\theta }&{2\sin \theta \cos \theta }\\ {{{\sin }^2}\theta }&{{{\cos }^2}\theta }&{ - \sin \theta \cos \theta }\\ { - \sin \theta \cos \theta }&{\sin \theta \cos \theta }&{{{\cos }^2}\theta - {{\sin }^2}\theta } \end{array}} \right]\left\{ {\begin{array}{*{20}{l}} {{\sigma _y}}\\ {{\sigma _z}}\\ {{\tau _{yz}}} \end{array}} \right\} $ | (6) |
式中:σr,σθ,τrθ分别为任意θ断面(如图 1)的径向应力、环向应力和剪应力;σy,σz,τyz分别为任意θ断面在整体坐标系的两个正应力和剪应力。
(2) 任意θ断面的轴力FN和弯矩M为:${F_N} = \int\limits_A {{\sigma _\theta }} {\rm{d}}A,M = \int\limits_A {{\sigma _\theta }l{\rm{d}}A} $其中:A为相应单元表面积(m2);l为单元形心到截面中性轴的距离(m)。
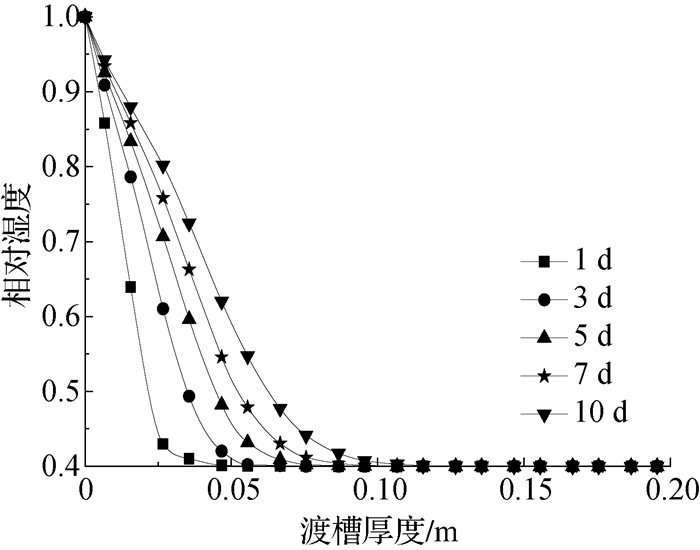
3 计算结果分析 3.1 湿度场分布规律为便于进行结构分析,通过有限元初步计算,选取湿度扩散深度值分别为0.05,0.07,0.08,0.09和0.10 m时,所对应的湿润时间分别为1,3,5,7和10 d情况下的湿度场分布进行分析,得到不同时刻混凝土渡槽沿径向槽壁厚度的湿度分布如图 3所示。由图 3可知,水分随时间的增加由渡槽内壁沿径向逐渐扩散,并沿径向槽壁厚度呈非均匀分布。在水分扩散过程中,相同时刻相对湿度沿径向逐渐减小,且扩散速率逐渐减小;在0~0.1 m范围内,同一位置渡槽厚度处,水分扩散速率随时间增加而逐渐减小,渡槽厚度在0.1~0.2 m时其湿度未发生变化,相对湿度为初始值0.4。
|
图 3 渡槽沿厚度方向相对湿度变化 Fig.3 Variation in relative humidity along wall thickness direction of aqueduct |
湿度会引起混凝土弹性模量变化并产生吸水膨胀。为探究湿度对渡槽变形的影响,取扩散深度为0,0.05,0.07,0.08,0.09和0.10 m时渡槽的横向变形进行分析,如图 4所示,图中“r”表示渡槽内水分扩散深度。

|
图 4 渡槽跨中横向变形 Fig.4 Aqueduct transverse deformation |
由图 4可知,渡槽横向(径向)变形水分未扩散时最大,最大值为0.24 mm位于圆心角10°处。受湿度影响,渡槽变形向内收缩,横向变形随水分扩散深度的增加而减小。当水分扩散深度分别为0.05,0.07,0.08,0.09和0.10 m时,横向变形最大值分别为0.191,0.159,0.140,0.129和0.118 mm,最大值分别位于圆心角15°,20°,24°,28°和31°,可明显看到横向变形最大值在减小,减幅为51%,作用位置也越来越趋于渡槽底部。由于拉杆作用,不同扩散深度时水面位置处的横向变形值不变,渡槽槽身底部端点处由于对称也无横向变形。
渡槽跨中及端肋断面底部顶点的纵向挠度如图 5所示。由图 5可知,跨中竖向挠度随时间先快速增大后缓慢增加。水分未扩散时,在槽身自重、水重及人行桥传至边梁的荷载作用下,跨中挠度值为0.41 mm;当扩散深度为0.01 m时,可明显看到挠度值快速增大到0.46 mm;随着水分不断浸入到渡槽内部0.1 m时,挠度值达到0.56 mm,较初始值增大了36.5%,原因是水分在0~1 d时,扩散较快,湿胀作用显著,后期吸水速率逐渐减小挠度增加较小。端肋处挠度值变化规律与跨中处类似,但其增幅较小,初始值为0.13 mm,扩散深度为0.01 m时,挠度值增大到0.15 mm;水分扩散深度为0.1 m时,挠度值增大到0.18 mm,较初始值增大了38.4%。由于端肋的限制槽壳变形较小,但在水分扩散作用下,挠度变化值较大。综合跨中和端肋断面处的挠度变形,湿度对渡槽变形作用明显。

|
图 5 渡槽挠度 Fig.5 Aqueduct longitudinal deflection |
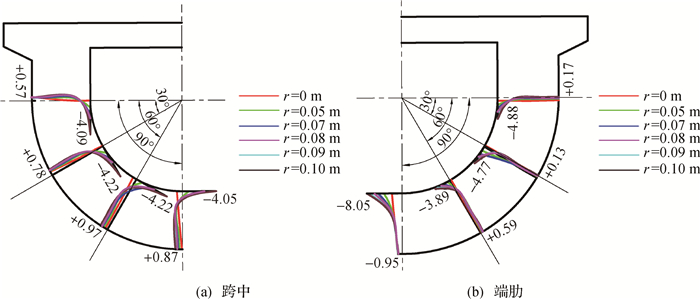
湿度作用下渡槽跨中及端肋断面处应力如图 6所示,图中数据指当扩散深度分别为0,0.05,0.07,0.08,0.09和0.10 m时的应力值。
|
图 6 跨中及端肋断面应力分布(单位:MPa) Fig.6 Stress distribution of transverse section in mid-span and end bearing (unit: MPa) |
由图 6(a)可知,槽底水分未扩散时内侧拉应力为0.66 MPa。当扩散深度为0.1 m时,内侧应力变化为压应力4.05 MPa,外侧拉应力由水分未扩散时的0.80 MPa增至0.87 MPa;0°,30°及60°截面与槽底截面规律类似,水分未扩散时槽身段各截面均处于全部受拉状态,内侧拉应力分别为0,0.05和0.46 MPa;当扩散深度为0.1 m时,内侧应力均变为压应力,分别达4.09,4.22和4.22 MPa,外侧拉应力分别由水分未扩散时的0.38,0.49和0.28 MPa增至0.45,0.78和0.97 MPa;受水分扩散影响且内侧湿度变化大于外侧湿度,导致内侧变形大于外侧变形,因此内侧压应力变化值大于外侧拉应力变化值,在30°以及60°截面处的内侧压应力最大。从图 6(b)可知,端肋处渡槽底水分未扩散时内侧压应力为2.32 MPa。当扩散深度为0.1 m时,内侧压应力值增到8.05 MPa,增加了2.46倍;而外侧压应力由水分未扩散时的0.80 MPa增至0.95 MPa;在圆心角为0°断面,内侧压应力0.70 MPa,外侧压应力0.58 MPa。在水分扩散深度为0.1 m时,内侧压应力增大5.97倍达到4.88 MPa,其外侧压应力也变为拉应力达到0.17 MPa;其余截面变化规律与0°截面规律近似,水分未扩散时为全部受压状态,随水分扩散深度增大,内侧压应力增大,外侧压应力减小或变为拉应力。在90°截面处压应力最大,且内侧压应力由顶部到底部先减后增,外侧应力由拉应力逐渐增大。结合图 3可知,渡槽内侧湿度大于外侧,湿胀使混凝土产生相对变形,内侧为压应力,外侧为拉应力,应力沿渡槽深度方向呈非线性变化。渡槽外侧拉应力虽小于C30的抗拉强度设计值2.01 MPa,但与其他荷载组合,可能超过混凝土抗拉强度,从而产生裂缝,破坏渡槽结构,因此需要提高混凝土等级或采取防水措施以减小湿度对渡槽的影响。
3.4 湿度对渡槽弯矩和轴力影响将图 6截面的应力转化为内力,更直观分析湿度影响。跨中及端肋断面处的内力如图 7所示。以通过圆心的z轴为界,左半部分数值表示弯矩,右半部分数值表示轴力。

|
图 7 跨中及端肋断面内力 Fig.7 Internal force of mid-span and end bearing sections |
渡槽跨中横向结构可简化为上部拉杆和下部渡槽槽身组成的3次超静定结构。由图 7(a)左侧部分可知, 在不考虑混凝土吸水膨胀时,上侧拉杆约束和水压共同作用下的渡槽跨中上部分外侧受拉,下部分内侧受拉。考虑混凝土吸水膨胀时,渡槽槽身在水分扩散过程中,内侧湿度始终比外侧的大,所以内侧吸水膨胀作用大于外侧。膨胀大的内侧受到膨胀小的外侧约束,故内侧应力为受压或拉应力减少;而膨胀小的外侧受到膨胀大的内侧的撑起作用,故外侧受拉。渡槽槽底水分未扩散时为负弯矩0.196 kN·m,水分扩散深度不断增大,槽身混凝土吸湿膨胀的进一步扩展,导致渡槽跨中上半部分外侧拉应力逐渐增大;当水分扩散深度为0.1 m时,弯矩较水分未扩散时增大到1.749 kN·m。
由图 7(a)左侧部分可知,渡槽直线段处的轴力值较小,最大值为0.820 kN;渡槽曲线段轴力越靠近底部轴力越大,但受水分扩散影响,轴力变化较小;槽底轴力水分未扩散时为15.951 kN,水分扩散深度为0.1 m时,轴力仅增大1.3%,达到16.171 kN。渡槽跨中结构整体可简化为无其他外部约束的薄壁结构,其跨中槽身处混凝土吸水膨胀相当于无外部约束的自由膨胀,故水分扩散对其跨中结构轴力影响不大。
由图 7(b)可知,渡槽直线段顶部产生了负弯矩,其值为-0.006 kN·m。水分扩散为0.1 m时,负弯矩增大到0.044 kN·m;对于渡槽曲线段,水分未扩散时在圆心角位于30°至70°之间存在负弯矩,但由于水分扩散影响,整个渡槽均处于正弯矩状态。渡槽槽底水分未扩散时弯矩值为0.822 kN·m,水分扩散深度为0.1 m时,其弯矩值增大到2.710 kN·m。由于端肋处槽身外侧受端肋约束,外侧拉应力变化比跨中的小,端肋处的弯矩变化明显比跨中变化小;而内侧膨胀时受到约束明显大于跨中,所以端肋处槽身内侧产生的压应力要比跨中的大,故端肋处的弯矩变化明显小于跨中。
由图 7(b)右侧部分可知,端肋轴力相比于跨中断面的轴力变化较大,端肋槽身可简化框式结构,但该薄壁结构受到端肋约束,其端肋槽身处混凝土吸水膨胀相当于被端肋紧紧地包裹住,其内部应力得不到释放,所以其逐渐增长,轴力逐渐变大。尤其是端肋槽身最低点,水分未扩散时轴力为68.359 kN,水分扩散为0.1 m时,轴力增大到89.094 kN,该处约束最为密集,同时又处于拱形顶点处,所以该处轴力变化幅度最大。
4 结语(1) 通过一维吸水试验率定混凝土扩散系数,基于Fick第二定律建立了混凝土试件湿度场表征模型,分析了渡槽的湿度分布规律。随着输水时间的延长,渡槽槽壁会产生一定湿润深度,湿润深度沿槽壁深度呈非均匀分布。
(2) 槽壁湿度的扩散程度会影响渡槽变形和应力分布。随湿润深度增加渡槽的纵向挠度有所增加,横向变形有所减小,横向效应大于纵向的影响程度。对于渡槽跨中横向断面来说,湿度增加了渡槽内侧湿胀压应力,使得水分未扩散时拉应力转化为压应力,但外侧拉应力则显著增大,不利于槽壁外侧抗裂。对于端肋处横断面,渡槽内壁湿度增大,进一步加大了内侧压应力,这对结构是有利的。
| [1] |
周继凯, 慕建磊, 严媛媛, 等. 早龄期混凝土内部湿度场的测量与数值模拟[J]. 科学技术与工程, 2013, 13(15): 4252-4256. ( ZHOU Jikai, MU Jianlei, YAN Yuanyuan, et al. Measurement and numerical simulation of internal humidity field in early-age concrete[J]. Science Technology and Engineering, 2013, 13(15): 4252-4256. DOI:10.3969/j.issn.1671-1815.2013.15.021 (in Chinese)) |
| [2] |
张鹏, 赵铁军, WITTMANNF H, 等. 基于中子成像的水泥基材料毛细吸水动力学研究[J]. 水利学报, 2011, 42(1): 81-87. ( ZHANG Peng, ZHAO Tiejun, WITTMANN F H, et al. Water capillary suction dynamics of cement-based materials based on neutron radiography method[J]. Journal of Hydraulic Engineering, 2011, 42(1): 81-87. (in Chinese)) |
| [3] |
黄海东, 王承启. 变湿度环境下的混凝土结构桥梁长期干缩行为[J]. 中国公路学报, 2016, 29(8): 77-84. ( HUANG Haidong, WANG Chengqi. Long term drying shrinkage behavior of concrete bridges under cyclic humidity conditions[J]. China Journal of Highway and Transport, 2016, 29(8): 77-84. DOI:10.3969/j.issn.1001-7372.2016.08.010 (in Chinese)) |
| [4] |
樊明哲. 湿胀变形对白水峪大坝坝踵应力变化的影响[J]. 水电与抽水蓄能, 2006, 30(2): 58-60. ( FAN Mingzhe. Impact of wet-expansion deformation on the stress of the heel of Baishuiyu dam[J]. Hydropower Automation and Dam Monitoring, 2006, 30(2): 58-60. DOI:10.3969/j.issn.1671-3893.2006.02.014 (in Chinese)) |
| [5] |
王志远, 费新峰, 沈慧, 等. 公伯峡堆石坝混凝土面板湿度变形研究[J]. 水电自动化与大坝监测, 2014, 38(5): 15-20. ( WANG Zhiyuan, FEI Xinfeng, SHEN Hui, et al. Study on concrete humidity deformation of face slab of Gongboxia CFRD[J]. Hydropower Automation and Dam Monitoring, 2014, 38(5): 15-20. DOI:10.3969/j.issn.1671-3893.2014.05.005 (in Chinese)) |
| [6] |
周耀, 王元丰, 韩冰.混凝土含水率对梁动力性能影响研究[C]//崔京浩.第19届全国结构工程学术会议论文集(第Ⅱ册).北京: 《工程力学》杂志社, 2010: 242-245. (ZHOU Yao, WANG Yuanfeng, HAN Bing. Study on the influence of concrete water content on the dynamic performance of beams[C]// CUI Jinghao. Proceedings of the Nineteenth National Conferences on Structural Engineering (No.Ⅱ). Beijing: Engineering Mechanics Press, 2010: 242-245. (in Chinese))
|
| [7] |
魏亚. 水泥混凝土路面板湿度翘曲形成机理及变形计算[J]. 工程力学, 2012, 29(11): 266-271. ( WEI Ya. Mechanism of moisture warping and deformation calculations in concrete pavements[J]. Engineering Mechanics, 2012, 29(11): 266-271. DOI:10.6052/j.issn.1000-4750.2011.04.0229 (in Chinese)) |
| [8] |
高翔, 魏亚. 水泥混凝土路面板湿度梯度模拟与分析[J]. 工程力学, 2014, 31(8): 183-188. ( GAO Xiang, WEI Ya. Modeling and analysis of moisture gradients in concrete pavements[J]. Engineering Mechanics, 2014, 31(8): 183-188. (in Chinese)) |
| [9] |
马跃先, 陈晓光. 水工混凝土的湿度场及干缩应力研究[J]. 水力发电学报, 2008, 27(3): 38-42. ( MA Yuexian, CHEN Xiaoguang. Research on humidity and drying shrinkage stresses of hydraulic concrete[J]. Journal of Hydroelectric Engineering, 2008, 27(3): 38-42. DOI:10.3969/j.issn.1003-1243.2008.03.008 (in Chinese)) |
| [10] |
李惠明, 邓春林, 方长远, 等. 沉管混凝土收缩及湿胀变形研究[J]. 水运工程, 2013(6): 24-28. ( LI Huiming, DENG Chunlin, FANG Changyuan, et al. Shrinkage and bulking of concrete for immersed tunnel[J]. Port and Waterway Engineering, 2013(6): 24-28. DOI:10.3969/j.issn.1002-4972.2013.06.007 (in Chinese)) |
| [11] |
白卫峰, 陈健云, 孙胜男. 孔隙湿度对混凝土初始弹性模量影响[J]. 大连理工大学学报, 2010, 50(5): 712-716. ( BAI Weifeng, CHEN Jianyun, SUN Shengnan. Effect of moisture in pore on initial elastic modulus of concrete[J]. Journal of Dalian University of Technology, 2010, 50(5): 712-716. (in Chinese)) |
| [12] |
侯东伟, 张君, 陈浩宇, 等. 干燥与潮湿环境下混凝土抗压强度和弹性模量发展分析[J]. 水利学报, 2012, 43(2): 198-208. ( HOU Dongwei, ZHANG Jun, CHEN Haoyu, et al. Development of strength and elastic modulus of concrete under moisture and drying curing conditions[J]. Journal of Hydraulic Engineering, 2012, 43(2): 198-208. (in Chinese)) |
| [13] |
王海龙, 李庆斌. 不同加载速率下干燥与饱和混凝土抗压性能试验研究分析[J]. 水力发电学报, 2007, 26(1): 84-89. ( WANG Hailong, LI Qingbin. Experiments of the compressive properties of dry and saturated concrete under different loading rates[J]. Journal of Hydroelectric Engineering, 2007, 26(1): 84-89. DOI:10.3969/j.issn.1003-1243.2007.01.017 (in Chinese)) |
| [14] |
MARTIN R P, METALSSI O O, TOUTLEMONDE F. Importance of considering the coupling between transfer properties, alkali leaching and expansion in the modelling of concrete beams affected by internal swelling reactions[J]. Construction and Building Materials, 2013, 49: 23-30. DOI:10.1016/j.conbuildmat.2013.08.008 |
| [15] |
苏安双, 宁逢伟, 韩旭东, 等. 含水率及加载速率对纤维增韧喷射混凝土弯曲韧性的影响[J]. 水利水运工程学报, 2013(5): 46-53. ( SU Anshuang, NING Fengwei, HAN Xudong, et al. Influences of moisture content and loading rate on flexural toughness of fiber reinforced shotcrete[J]. Hydro-Science and Engineering, 2013(5): 46-53. DOI:10.3969/j.issn.1009-640X.2013.05.007 (in Chinese)) |
| [16] |
刘道维, 刘本义, 李向东, 等. 硫酸盐和干湿循环耦合作用下混凝土性能研究[J]. 水利水运工程学报, 2015(4): 69-74. ( LIU Daowei, LIU Benyi, LI Xiangdong, et al. Property analysis of concrete under coupling action of sulfate and wet-dry cycles[J]. Hydro-Science and Engineering, 2015(4): 69-74. (in Chinese)) |
| [17] |
BAZANT Z P, NAIJAR L J. Nonlinear water diffusion in nonsaturated concrete[J]. Materiaux Et Construction, 1972, 5(1): 3-20. DOI:10.1007/BF02479073 |
| [18] |
KIM J K, LEE C S. Moisture diffusion of concrete considering self-desiccation at early ages[J]. Cement and Concrete Research, 1999, 29(12): 1921-1927. DOI:10.1016/S0008-8846(99)00192-1 |
| [19] |
杨乐, 李宗利, 姚希望, 等. 湿度对混凝土简支梁受力变形影响研究[J]. 水力发电学报, 2019, 38(3): 218-226. ( YANG Le, LI Zongli, YAO Xiwang, et al. Influence of humidity on stress and deformation of simply supported concrete beams[J]. Journal of Hydroelectric Engineering, 2019, 38(3): 218-226. (in Chinese)) |
| [20] |
朱俊阁.湿度对混凝土梁受力性能影响研究[D].杨凌: 西北农林科技大学, 2016. (ZHU Junge. Study on the influence of humidity on the mechanical performance of concrete beams[D]. Yangling: Northwest A & F University, 2016. (in Chinese))) http://cdmd.cnki.com.cn/Article/CDMD-10005-1016785668.htm
|
| [21] |
沈关林, 胡更开. 复合材料力学[M]. 北京: 清华大学出版社, 2006: 52-53. ( SHEN Guanlin, HU Gengkai. Composite mechanics[M]. Beijing: Tsinghua University Press, 2006: 52-53. (in Chinese))
|
 2019
2019 

