2. 南昌大学 建筑工程学院,江西 南昌 330031
高拱坝结构大多位于深山峡谷河流中,泄流时的单宽流量大,洪峰能量高,泄洪诱发振动是关系拱坝坝身安全的重大关键技术问题[1-2]。然而,由于高拱坝泄流结构激励困难、数据采集工作环境复杂等,实测泄流结构的振动响应数据中不可避免存在一些噪声,对振动响应数据的分析精度有较大影响。因此,消除或者降低环境背景噪声影响对于分析泄流结构的振动响应具有很大意义。
针对泄流结构的滤波降噪处理,在国内外学者共同探讨下,先后采用了傅里叶变换,小波变换,经验模态分解等方法。早期杨丽娟等[3-4]根据信号频率分布,采用傅里叶变换进行滤波,但傅里叶变换忽略时域信息对整个时域进行变换,对于非平稳信号不能很好处理;唐进元等[5-7]利用小波分析进行信号去噪,小波变换常用小波阈值滤波方法进行降噪,其滤波效果主要取决于小波阈值的选择,对于非平稳信号不能达到预期效果;何文平等[8-10]采用EMD方法对信号进行降噪,其无须预先设定任何基函数,仅依据信号自身频率特征进行分解,信噪比很高,但对混入了白噪声的信号,容易造成有效信息的丢失;张建伟等[11-12]研究了小波分析和EMD联合去噪方法,能有效提取低信噪比泄流结构的价值信息,但小波基难以确定;李成业等[13-14]研究了基于EMD方法的小波阈值滤波去噪方法,应用EMD完全自适应性来弥补小波在非平稳信号处理中的不足,但信号中含有有声噪声或白噪声时,先进行EMD分解会出现不同程度的端点效应及模态混叠问题[15]。
在以上研究基础上,经过理论分析以及对高拱坝泄流结构仿真试验,本文试图提出一种基于改进小波阈值-EMD联合算法的滤波降噪方法。首先利用改进的小波阈值算法滤除实测振动响应信号中的高频白噪声,降低EMD的端点效应及模态混叠问题,然后进行EMD分解,采用DFA方法对白噪声及低频水流噪声进一步滤除。最后,将该方法应用于高拱坝结构的实测振动响应分析。
1 基于改进的小波阈值-EMD联合算法降噪方法 1.1 改进的小波阈值-EMD联合算法基本原理小波阈值降噪[16-17]是寻找对原始信号的最佳逼近,依赖于所选择的小波基、小波分解层数、阈值函数和阈值选取准则。小波阈值算法精度的高低除了阈值函数的选取,还和小波阈值大小的估计有关,若阈值太小,则信号降噪不完整;反之,阈值太大,原始信号特征将被抑制,导致信号重构时发生偏差,影响降噪效果。其主要思想是根据预设阈值压缩信号的小波变化系数,在降噪后重构系数,以达到降噪目的。
关于小波阈值T的选取,传统小波阈值降噪方法的阈值选择方式为:
| $ T = {\sigma _{\rm{n}}}\sqrt {2\ln V} $ | (1) |
式中:σn为标准方差;N为信号长度。
EMD算法[18]的实现过程是通过对信号x(t)采用3次样条插值的方法筛选迭代地分解出若干个IMF分量和1个残余信号。这些IMF分量具有以下特征:整个信号的极值点和零点交叉的最大数量不超过1;由信号任意一点的极大值和极小值确定的上下包络线平均值为0。信号x(t)可表示为:
| $ x(t) = \sum\limits_{j = 1}^n {IM{F_j}} (t) + {r_n}(t) $ | (2) |
式中:n为IMF分量的数量;rn(t)为x(t)的残余信号。
IMF分量的迭代筛选[19]是EMD分解的重要环节。根据EMD分解的正交性,若分解正确,则各IMF分量之间相互正交,定义IMF正交指数为:
| $ IO = \sum\limits_{t = 0}^T {\left( {\sum\limits_{i = 1}^{n + 1} {\sum\limits_{j = 1}^{n + 1} {IM{F_i}} } (t) \times IM{F_j}(t)/x{{(t)}^2}} \right)} $ | (3) |
若正交指数很小,表明模态分量互不相关,没有模态混叠产生,反之模态混叠严重。以正交指数作为IMF筛选准则可定量评价分解过程中模态混叠的程度,保证分解的正交性减少分解过程中的能量泄露,使分解出的IMF分量更接近其实际的物理意义。
1.2 基于改进小波阈值-EMD联合算法的信号降噪实测的泄流结构响应中往往混有低频大波干扰信号和白噪声,为更多地保留原信号中的有用信号,同时降低模态混叠的影响,提出改进的小波阈值-EMD联合滤波方法对拱坝泄流结构响应进行滤波降噪。该方法结合了小波阈值算法和EMD算法的优点,首先利用改进的小波阈值算法滤除信号中的高频白噪声,降低EMD的端点效应及模态混叠,然后进行EMD分解,采用DFA方法对白噪声及低频水流噪声进一步滤除,以提高滤波精度和降噪效果。其实质在于根据有效特征信息和噪声在小波分解尺度和EMD分解空间上的不同规律,保留有效特征信息的同时抑制噪声,从而达到信号降噪的目的。其中,小波阈值以及阈值函数的选取在处理过程中尤为关键。小波阈值设置的目的主要是将高频系数中的噪声分量分离出去,理想的阈值应刚好等于临界值,将噪声分量彻底消除,同时能保留原始有用信号。
因信号小波系数在不同层的阈值各异,通过白噪声检验[20]确定分解层数j,根据不同的分解层数,设计各层阈值的选取函数。对被噪声淹没的泄流结构振动信号,噪声的小波系数随分解层数的增加不断降低而影响降噪效果,而传统的阈值公式计算的是全局阈值,显然不适合本文降噪处理,故对阈值公式进行改进,具体如下:
| $ T = t\sigma \exp (\sigma ){N_j}\sqrt {2\lg {N_j}} /\lg (j + 1) $ | (4) |
式中:Nj为信号数据长度;j为小波分解层数;σ为标准方差,其计算式如下:
| $ \sigma = {\rm{median}}\left( {{\rm{abs}}\left( D \right)} \right)/0.5 \times {N_j} $ | (5) |
式中:D为高频系数的绝对中值。
传统的阈值函数有软阈值和硬阈值函数两种。其中,硬阈值函数是当小波系数绝对值大于或等于给定阈值时,令其保持不变,否则将其置零,其计算式如下:
| $ {\hat w_{j,k}} = \left\{ {\begin{array}{*{20}{c}} {{w_{j,k}},\left| {{w_{j,k}}} \right| \ge T}\\ {0,\left| {{w_{j,k}}} \right| < T} \end{array}} \right. $ | (6) |
式中:${\hat w_{j,k}}$为施加阈值后的估计小波系数;wj, k为信号的小波分解系数。
软阈值函数是当小波系数的绝对值大于或等于给定阈值时,令其减去阈值,否则将其置零,其计算式如下:
| $ {\hat w_{j,k}} = \left\{ {\begin{array}{*{20}{l}} { {\rm sgn} \left( {{w_{j,k}}} \right)\left( {\left| {{w_{j,k}}} \right| - T} \right),\left| {{w_{j,k}}} \right| \ge T}\\ {0,\left| {{w_{j,k}}} \right| < T} \end{array}} \right. $ | (7) |
硬阈值函数能很好地保持信号边缘等局部特征,但易出现伪吉布斯现象。软阈值函数处理相对平滑,但会造成失真现象,如边缘模糊等。为充分发挥小波降噪性能,针对软阈值和硬阈值函数的不足,提出了一种改进的小波阈值函数,其定义如下:
| $ {\hat w_{j,k}} = \left\{ {\begin{array}{*{20}{l}} { {\rm sgn} \left( {{w_{j,k}}} \right)\left[ {\left| {{w_{j,k}}} \right| - tT{\rm exp} \left( {(1 - t)\left( {T - \left| {{w_{j,k}}} \right|} \right)} \right)} \right],\left| {{w_{j,k}}} \right| \ge T}\\ {0,\left| {{w_{j,k}}} \right| < T} \end{array}} \right. $ | (8) |
式中:t为调整因子。
当|wj, k|≥T时,可以得到如下函数:
| $ f(x) = {\rm sgn} (x)[|x| - tT{\rm exp} ((1 - t)(T - |x|))] $ | (9) |
且有,
| $ \left\{ \begin{array}{l} \frac{{f(x)}}{x} = \frac{{[x - tT\exp ((1 - t)(T - x))]}}{x} = 1 - \frac{{tT\exp ((1 - t)(T - x))}}{x} \to 1(x \to + \infty ),x > 0\\ \frac{{f(x)}}{x} = \frac{{[x + tT\exp ((1 - t)(T + x))]}}{x} = 1 + \frac{{tT\exp ((1 - t)(T + x))}}{x} \to 1(x \to - \infty ),x < 0 \end{array} \right. $ | (10) |
改进阈值函数相当于介于硬阈值和软阈值函数间的一个函数,当信号中存在大量突变时,T移往硬阈值方向;相反,当信号比较平滑时,T移往软阈值方向。通过自适应调整阈值T的大小设计其阈值函数,以求获得良好的降噪效果。
为增加EMD分解的密频识别能力,采用正交指数取代传统阈值参数控制IMF筛选过程,不同IMF筛选迭代次数使正交指数IO达到最小值,即:
| $ x\left( {N'} \right) = {\rm argmin} \left( {{I_{\rm{O}}}} \right) $ | (11) |
式中:N′为每阶IMF筛选迭代的次数。
EMD用于降噪的方法主要有直接重构法和阈值滤波法等,而文中采取去趋势波动分析(DFA)[21-23]对IMF分量阈值进行自适应选取,进一步滤除白噪声。去趋势波动分析方法是测量非平稳时间序列的长期依赖性的成功方法。特殊情况αi=0.5,αi=1.0和αi=1.5对应完全不相关的白噪声, 粉红噪声和布朗噪音(αi为DFA指数)。当0 < αi < 0.5时, 信号被称为“反关联”, 即意味着大波动之后很可能跟随着小波动。当αi从0.5增加到1.0时,时间相关性是持久的。如果αi>1.0, 相关性不表现出幂律的行为。利用DFA指数对EMD分解的IMF分量判别其阈值,理论上,当0 < αi < 0.5时,其所对应的序列即为白噪声序列,0.5 < αi < 1.0为粉红噪声,1.0 < αi < 1.5为布朗噪声。泄流结构振动响应数据的噪声大部分为白噪声,文中仅考虑白噪声情况。对于白噪声的阈值取为0 < αi < 0.5。其中,计算αi指数的计算式为:
| $ {\alpha _i} = \frac{{{{\log }_2}F(s)}}{{{{\log }_2}s}} = \frac{{{{\log }_2}{{\left[ {\frac{1}{{2{N_{\rm{s}}}}}\sum\limits_{v = 1}^{2{N_{\rm{s}}}} {{F^2}} (v,s)} \right]}^{\frac{1}{2}}}}}{{{{\log }_2}s}} $ | (12) |
式中:s为IMF分量的子区间长度; Ns=N/s; F2(v, s)为IMF分量的消除趋势平均值; F(s)为F2(v, s)的均值平方根。
含噪信号进行EMD分解后,通过IMF频谱分析,将振动能量集中在0.5 Hz以下的低频干扰信号予以滤除,计算剩余IMFi的αi指数,进一步滤除白噪声序列,将其他层IMF与余项的重构,所得信号即为滤波降噪后的泄流振动信号。
2 基于改进小波阈值-EMD与RDT算法的降噪流程基于上述分析,改进的Wavelet-EMD与RDT算法的高拱坝泄流结构工作模态识别步骤与计算流程如下:
Step1:通过白噪声检验确定分解层数j,将信号进行小波分解,根据式(4)计算不同各层阈值。
Step2:根据式(10)设计其阈值函数,进行阈值降噪处理。降噪后进行小波系数重构,得到降噪后信号xw(n)。
Step3:对xw(n)进行EMD分解,得到n层本征模态函数{IMFi}(i=1, 2, …, L)和余项rn。
Step4:对每层本征模态函数IMFi进行功率谱分析,滤除频率小于0.5 Hz的低频水流噪声。
Step5:利用去趋势波动分析的方法计算剩余IMFi的αi指数。将0 < αi < 0.5区间的IMFi予以滤除。将αi>0.5的IMFi及其余项重构,即得到降噪后的振动响应信号。
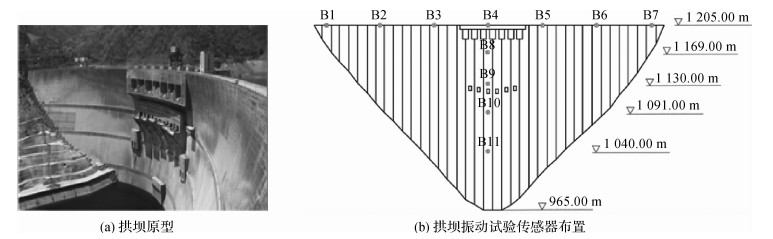
3 实例考证 3.1 工程资料某拦河坝为典型高拱坝,最大坝高240 m,其原型如图 1(a)所示。为准确获得拱坝工作性态,将测点布置于坝顶拱圈及拱冠梁处,其中,在拱圈处自左岸到右岸分别布置7个水平动位移测点,编号为B1-B7;沿拱冠梁自坝顶到坝底分别布置4个水平动位移测点,编号为B8~B11,测点分布情况见图 1(b)。其中动位移传感器为DP地震式低频位移传感器,其频响范围0.35~200 Hz,灵敏度8~15 mv/μm不等。采用DASP数据采集和处理系统进行数据采集,采样频率为200 Hz,采样时间为300 s,共采集60 000个数据点。选取了较为典型的5种测试工况,对坝体的泄洪振动进行原型观测(见表 1)。根据该拱坝位移监测获取的采样数据,进行了新方法的探讨。
|
图 1 拱坝原型泄洪振动测点布置 Fig.1 Layout of vibration measuring poins for flood discharge of prototype arch dam |
| 表 1 拱坝原型泄洪振动测试工况 Tab.1 Test working conditions of flood releasing-induced vibration of prototype arch dam |
由于在泄流激励下拱坝泄流结构的振动响应数据采集过程中,容易混入许多其他干扰信号而掩盖所需的有用信号,进而影响测试结果的振动响应分析精度。通过分析各工况的实测数据,发现靠近坝肩的测点更容易受噪声干扰,例如工况5情况下的B2,B6测点。为验证本文方法对于拱坝泄流结构降噪处理的合理性和准确性,分别对B2,B4和B6测点进行分析。
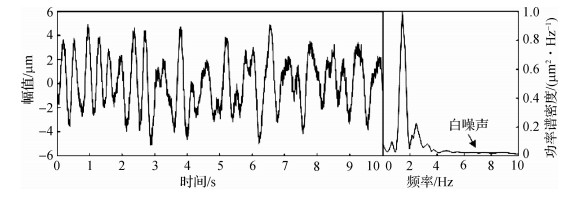
3.2 改进的小波阈值-EMD联合算法的信号降噪处理取该拱坝工况5情况下B2实测位移信号数据进行分析,获得其原始含噪信号及其归一化功率谱密度曲线如图 2所示。
|
图 2 原始信号时程及其归一化频率谱曲线(部分) Fig.2 Time history of original signal and its normalized frequency spectrum curves (part) |
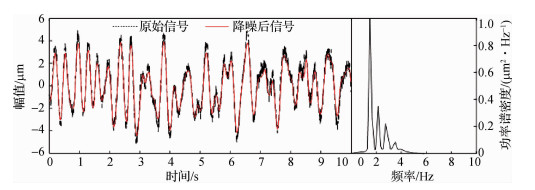
由原信号的时程图以及功率谱密度曲线可知,原信号中存在大量白噪声以及低频水流噪声。根据原信号特性,选取小波分解层数为6层,运用文中设计的阈值函数对信号进行小波阈值降噪,以及进行小波系数重构得到滤除高频白噪声的信号。再进行EMD降噪进一步滤除白噪声及低频水流噪声:信号经EMD分解得到12个IMF分量,对其进行功率谱分析,第1~3分量频率小于0.5 Hz,属于低频水流噪声,直接予以删除;然后对剩余每个IMF分量进行DFA指数判别,其具体DFA指数如表 2所示。剔除=αi < 0.5的分量,将αi>0.5的IMFj及其余项进行重构,即得到降噪后的振动响应信号。滤除全部噪声后的时程图及其归一化功率谱密度曲线见图 3所示。
| 表 2 IMF分量的DFA指数 Tab.2 DFA index of each IMF component |
|
图 3 B2测点降噪后时程及其归一化功率谱曲线 Fig.3 Time history and normalized power spectrum curves after noise reduction of B2 measuring point |
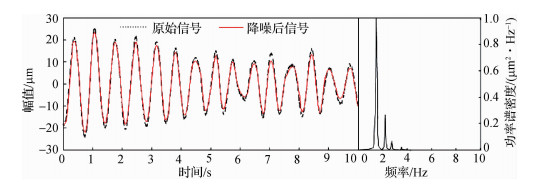
限于篇幅,此处不再叙述B4,B6测点的降噪过程,其降噪结果如图 4和5所示。
|
图 4 B4测点降噪后时程及其归一化功率谱曲线 Fig.4 Time history and normalized power spectrum curves after noise reduction of B4 measuring point |
|
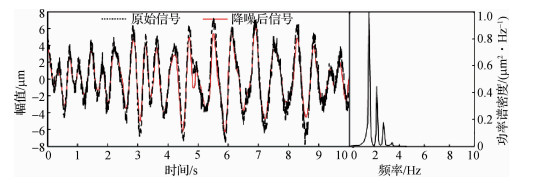
图 5 B6测点降噪后时程及其归一化功率谱曲线 Fig.5 Time history and normalized power spectrum curves after noise reduction of B6 measuring point |
B2和B6测点位于该拱坝靠近坝肩位置,所测信号易受噪声干扰;B4测点位于拱冠梁中部,噪声干扰较其余两点小。从不同位置、不同噪声干扰情况的3个测点滤波前后时程曲线对比可知,原拱坝时程图中的由干扰信号引起的毛刺已被基本消除;由功率谱可知,B3测点的原功率谱中存在许多干扰信号,例如低频干扰信号和白噪声信号,滤波后的新功率谱中,0.5 Hz以下的低频干扰信号已被剔除,而且白噪声部分也很好地被剔除了。3个测点滤波降噪后的信号功率谱,均在1.4,2.2和2.8 Hz等处存在明显峰值,表明该降噪方法能较好地保留信号的特征信息,精确提取泄流结构工作特征信息,具有较好的工程实用性。
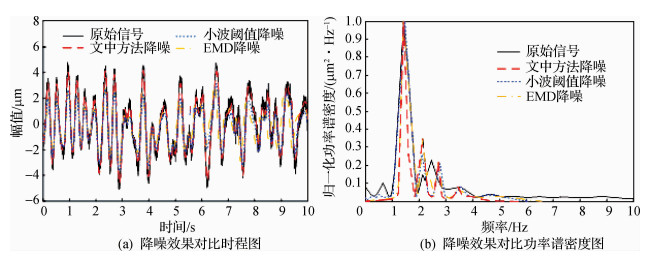
为进一步验证该降噪方法的有效性和优越性,以B2测点为例,分别利用小波阈值降噪,EMD降噪以及改进的Wallet-EMD联合降噪对该拱坝泄流振动响应信号进行处理,结果如图 6。
|
图 6 3种方法降噪效果对比 Fig.6 Comparison of three methods for noise reduction effects |
从图 6可以看出,相较其他两种降噪方法,改进的小波阈值-EMD联合降噪效果最好。小波阈值降噪只能滤除高频噪声,不能滤除低频水流噪声,使得部分信号受到较大损失,没有实现较好的滤波效果。而EMD方法能有效滤除低频水流噪声,但白噪声的存在,使得EMD分解时容易造成模态混叠而影响滤波结果。而采用基于改进的小波阈值-EMD联合算法的滤波降噪方法,先利用改进的小波阈值算法滤除信号中的高频白噪声,降低EMD的端点效应及模态混叠,然后进行EMD降噪,采用DFA方法进一步滤除白噪声及低频水流噪声,最大程度地保留了信号中的有效特征信息。因此,改进的小波阈值-EMD联合算法适合于分析高拱坝泄流结构振动响应信号的滤波降噪。
4 结语(1) 利用改进的小波阈值-EMD联合算法对高拱坝实测振动响应资料进行降噪处理。先采用改进的小波阈值算法,克服了软、硬阈值函数选取的缺陷,有效剔除高频白噪声的同时降低了模态混叠的影响;再利用EMD降噪进一步滤除了白噪声及低频水流噪声,提高了滤波降噪的精度。
(2) 针对高拱坝泄流结构的原型振动响应信号,提出的改进小波阈值-EMD联合算法能在有效去除高频白噪声与低频水流噪声的同时,更好地保留了信号中的有效特征信息,与小波阈值及EMD等方法相比,降噪效果更好且较实用。
| [1] |
LI HK, WANG Y J, WEI B W. Inversion algorithm for the whole prototype dynamic displacement field of a high arch dam based on limited measuring points[J]. Journal of Vibration and Control, 2016, 23(20): 3431-3447. |
| [2] |
李成业, 刘昉, 马斌, 等. 基于改进HHT的高拱坝模态参数识别方法研究[J]. 水力发电学报, 2012, 31(1): 48-55. ( LI Chengye, LIU Fang, MA Bin, et al. Study on modal parameters identification method of high arch dam based on improved Hilbert-Huang transform[J]. Journal of Hydroelectric Engineering, 2012, 31(1): 48-55. (in Chinese)) |
| [3] |
司祯祯. 傅里叶变换与小波变换在信号去噪中的应用[J]. 电子设计工程, 2011, 19(4): 155-157. ( SI Zhenzhen. Application of Fourier transform and wavelet transform in signal de-noising[J]. Electronic Design Engineering, 2011, 19(4): 155-157. DOI:10.3969/j.issn.1674-6236.2011.04.045 (in Chinese)) |
| [4] |
杨丽娟, 张白桦, 叶旭桢. 快速傅里叶变换FFT及其应用[J]. 光电工程, 2004, 31(增刊1): 1-3, 7. ( YANG Lijuan, ZHANG Baihua, YE Xuzhen. Fast Fourier transform and its applications[J]. Opto-Electronic Engineering, 2004, 31(Suppl1): 1-3, 7. (in Chinese)) |
| [5] |
唐进元, 陈维涛, 陈思雨, 等. 一种新的小波阈值函数及其在振动信号去噪分析中的应用[J]. 振动与冲击, 2009, 28(7): 118-121, 217. ( TANG Jinyuan, CHEN Weitao, CHEN Siyu, et al. Wavelet-based threshold vibration signal de-noising with a new adaptive thresholding function[J]. Journal of Vibration and Shock, 2009, 28(7): 118-121, 217. DOI:10.3969/j.issn.1000-3835.2009.07.025 (in Chinese)) |
| [6] |
刘志松. 基于小波分析的信号去噪方法[J]. 浙江海洋学院学报(自然科学报), 2011, 30(2): 150-154. ( LIU Zhisong. Signal de-noising based on the wavelet transform[J]. Journal of Zhejiang Ocean University (Natural Science), 2011, 30(2): 150-154. (in Chinese)) |
| [7] |
LIU Xiuping, YUAN Wei, HAN Lili, et al. X-ray pulsar signal de-noising for impulse noise using wavelet packet[J]. Aerospace Science and Technology, 2017, 64: 147-153. DOI:10.1016/j.ast.2017.01.024 |
| [8] |
赵雯雯, 曾兴雯. 一种新的EMD去噪方法[J]. 电子科技, 2008, 21(5): 30-32, 36. ( ZHAO Wenwen, ZENG Xingwen. A new signal de-noising method based on Empirical Mode Decomposition (EMD)[J]. Electronic Science and Technology, 2008, 21(5): 30-32, 36. DOI:10.3969/j.issn.1007-7820.2008.05.009 (in Chinese)) |
| [9] |
HE X H, HUA X G, CHEN Z Q, et al. EMD-based random decrement technique for modal parameter identification of an existing railway bridge[J]. Engineering Structures, 2011, 33(4): 1348-1356. DOI:10.1016/j.engstruct.2011.01.012 |
| [10] |
DYBALA J, ZIMROZ R. Rolling bearing diagnosing method based on Empirical Mode Decomposition of machine vibration signal[J]. Applied Acoustics, 2014, 77(3): 195-203. |
| [11] |
张建伟, 江琦, 赵瑜, 等. 一种适用于泄流结构振动分析的信号降噪方法[J]. 振动与冲击, 2015, 34(20): 179-184. ( ZHANG Jianwei, JIANG Qi, ZHAO Yu, et al. De-noising method for vibration signal of flood discharge structures[J]. Journal of Vibration and Shock, 2015, 34(20): 179-184. (in Chinese)) |
| [12] |
程知, 何枫, 张巳龙, 等. 趋势项调制的小波-经验模态分解联合方法用于大气相干长度廓线去噪[J]. 光学学报, 2017, 37(12): 15-26. ( CHENG Zhi, HE Feng, ZHANG Silong, et al. Combination method of wavelet and empirical mode decomposition with trend modulation used for atmospheric coherent length profile de-noising[J]. Acta Optica Sinica, 2017, 37(12): 15-26. (in Chinese)) |
| [13] |
李成业, 练继建, 刘昉, 等. EMD与小波阈值联合滤波方法的改进及其在泄流结构振动分析中的应用[J]. 振动与冲击, 2013, 32(19): 63-70, 110. ( LI Chengye, LIAN Jijian, LIU Fang, et al. An improved filtering method based on EMD and wavelet threshold and its application in vibration analysis for a flood discharge structure[J]. Journal of Vibration and Shock, 2013, 32(19): 63-70, 110. DOI:10.3969/j.issn.1000-3835.2013.19.012 (in Chinese)) |
| [14] |
于金涛, 赵树延, 王祁. 基于经验模态分解和小波变换声发射信号去噪[J]. 哈尔滨工业大学学报, 2011, 43(10): 88-92. ( YU Jintao, ZHAO Shuyan, WANG Qi. De-noising of acoustic emission signals based on empirical mode decomposition and wavelet transform[J]. Journal of Harbin Institute of Technology, 2011, 43(10): 88-92. DOI:10.11918/j.issn.0367-6234.2011.10.019 (in Chinese)) |
| [15] |
胡爱军, 孙敬敬, 向玲. 经验模态分解中的模态混叠问题[J]. 振动、测试与诊断, 2011, 31(4): 429-533. ( HU Aijun, SUN Jingjing, XIANG Ling. Modal mixing in empirical mode decomposition[J]. Journal of Vibration, Measurement and Diagnosis, 2011, 31(4): 429-533. DOI:10.3969/j.issn.1004-6801.2011.04.006 (in Chinese)) |
| [16] |
WEI B W, YUAN D Y, LI H K, et al. Combination forecast model for concrete dam displacement considering residual correction[J]. Structural Health Monitoring, 2019, 18(1): 232-244. DOI:10.1177/1475921717748608 |
| [17] |
WEI B W, YUAN D Y, LI H K, et al. Modified hybrid forecast model considering chaotic residual errors for dam deformation[J]. Structural Control and Health Monitoring, 2018, 25(8): e2188. DOI:10.1002/stc.2188 |
| [18] |
YANG J, LI P, YANG Y, et al. An improved EMD method for modal identification and a combined static-dynamic method for damage detection[J]. Journal of Sound and Vibration, 2018, 420: 242-260. DOI:10.1016/j.jsv.2018.01.036 |
| [19] |
荣钦彪, 刘昉, 宿策, 等. EMD密集模态识别研究及在电站厂房中的应用[J]. 水力发电学报, 2017, 36(6): 103-113. ( RONG Qinbiao, LIU Fang, SU Ce, et al. EMD identification of closely-spaced modes and its application to power plant analysis[J]. Journal of Hydroelectric Engineering, 2017, 36(6): 103-113. (in Chinese)) |
| [20] |
李炜, 陈晓辉, 毛海杰. 小波阈值消噪算法中自适应确定分解层数研究[J]. 计算机仿真, 2009, 26(3): 311-313, 336. ( LI Wei, CHEN Xiaohui, MAO Haijie. A study of adaptive optimal decomposition level in threshold de-noising algorithm based on wavelet transform[J]. Journal of Computer Simulation, 2009, 26(3): 311-313, 336. DOI:10.3969/j.issn.1006-9348.2009.03.080 (in Chinese)) |
| [21] |
MERT A, AKAN A. Detrended fluctuation thresholding for empirical mode decomposition based de-noising[J]. Digital Signal Processing, 2014, 32: 48-56. DOI:10.1016/j.dsp.2014.06.006 |
| [22] |
何文平, 吴琼, 成海英, 等. 不同滤波方法在去趋势波动分析中去噪的应用比较[J]. 物理学报, 2011, 60(2): 029203. ( HE Wenping, WU Qiong, CHENG Haiying, et al. Comparison of applications of different filter methods for de-noising detrended fluctuation analysis[J]. Acta Phys Sinica, 2011, 60(2): 029203. (in Chinese)) |
| [23] |
刘付斌, 高相铭. 基于EEMD与DFA的Hurst指数估计[J]. 测控技术, 2013, 32(10): 98-101. ( LIU Fubin, GAO Xiangming. Estimation of hurst index based on EEMD and DFA[J]. Measurement and Control Technology, 2013, 32(10): 98-101. DOI:10.3969/j.issn.1000-8829.2013.10.027 (in Chinese)) |
2. College of Civil Engineering and Architecture, Nanchang University, Nanchang 330031, China
 2019
2019 