2. 南水北调东线江苏水源有限责任公司,江苏 南京 210019;
3. 徐州市水利建筑设计研究院,江苏 徐州 221000
出水流道作为大型低扬程泵站中与水泵导叶体紧密相连的过流通道,承担着回收水流动能、优化出水流态的重要任务。流道水头损失对泵装置效率有显著影响,而出水流道水头损失在流道总损失中所占比重较大,为此出水流道水力设计在低扬程泵站工程建设中广受关注[1-2]。随着计算流体动力学(CFD)的发展和商用软件的开发应用,数值模拟方法在泵站前池、水泵和流道设计及水力性能计算中得到了越来越多的应用[3-4]。
三维湍流流动数值计算结果的准确性受所采用湍流模型的影响,目前已有不少学者致力于数值计算湍流模型的适用性研究并取得了一些成果:王福军等[5]系统分析了各个湍流计算模型的特点及应用可能性; 张德胜等[6]证明了Standard k-ε,RNG k-ε和RSM湍流模型在轴流泵流场中的适用性; 王洋等[7]研究表明RNG k-ε湍流模型最适合低转速离心泵的数值计算,SST k-ω湍流模型次之; 丛国辉等[8]证明了Realizable k-ε湍流模型对进水池内旋涡状态预测与试验值最为接近,比Standard k-ε,RNG k-ε湍流模型更适用; 印超[9]使用不同的k-ε湍流模型对泵站弧形弯道前池进行研究,得到了Standard k-ε湍流模型更适用的结论。可见,已有文献对泵站前池、进水池和水泵水力性能数值计算的湍流模型适用情况进行了研究,而针对大型低扬程泵站出水流道数值计算湍流模型的选择还未进行研究。本文以大型低扬程泵站常用的虹吸式出水流道为研究对象,以出水流道水力性能模型试验结果为基准,将不同湍流模型下的流道水力性能定常数值计算结果与模型试验结果进行比对分析,为虹吸式出水流道水力性能数值计算提供参考。
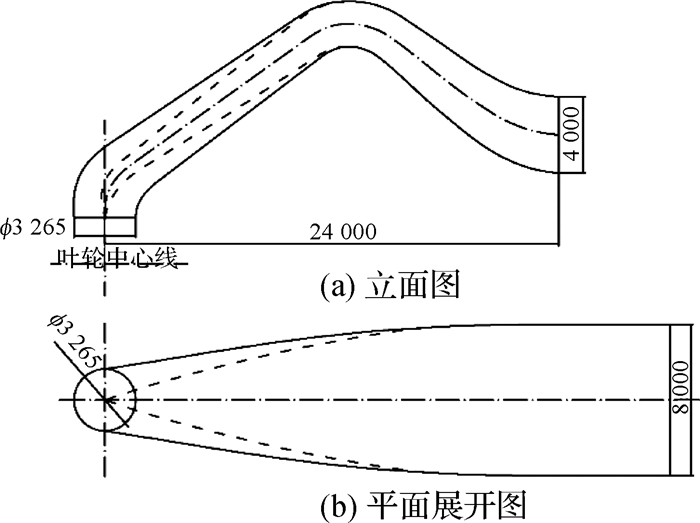
1 虹吸式出水流道几何参数虹吸式出水流道的断流简单可靠、水力性能优异且运行维护方便[10],在低扬程泵站中广泛应用。南水北调东线工程某大型低扬程泵站设计流量165 m3/s,设计扬程5.5 m,该站采用立式安装全调节轴流泵6台套,单泵设计流量33 m3/s,水泵叶轮直径3.15 m,进水流道采用肘形进水流道、出水采用虹吸式出水流道。该站虹吸出水流道单线图示于图 1,流道进口断面直径3.265 m,水平长24 m,出口断面宽度和高度分别为4和8 m。
|
图 1 虹吸式出水流道单线图(单位:mm) Fig.1 Single line diagram of siphon outlet conduit (unit: mm) |
出水流道模型试验装置为立式循环系统,由模型泵、出水流道、出水箱、电磁流量计和连接管道等组成。试验装置由模型泵供水以模拟原型水泵出水流态,通过变频器调节工况; 流道模型进口断面直径为150 mm,流道模型基于几何相似原理按原型、模型进口断面直径之比采用便于观察水流流态的透明有机玻璃加工制作。在距流道模型进口断面前一定距离处设置进口测压断面、在距流道出口断面足够远的出水池中设置出口测压断面,以满足水流测压所要求的渐变流条件; 试验流量通过LDY型电磁流量计直接读出,流量测量的满量程误差为±0.5%;在模型泵出口设置旋度计并连接二次仪表测量模型泵出口水流所具有的速度环量,以计算导叶体出口所具有的切向动能。关于出水流道模型试验装置及测试方法详见文献[11],该出水流道水力损失测试综合误差为±2.60%。为了观察出水流道内流态,在出水流道内壁粘贴红色细丝线,丝线可随水流自由摆动。
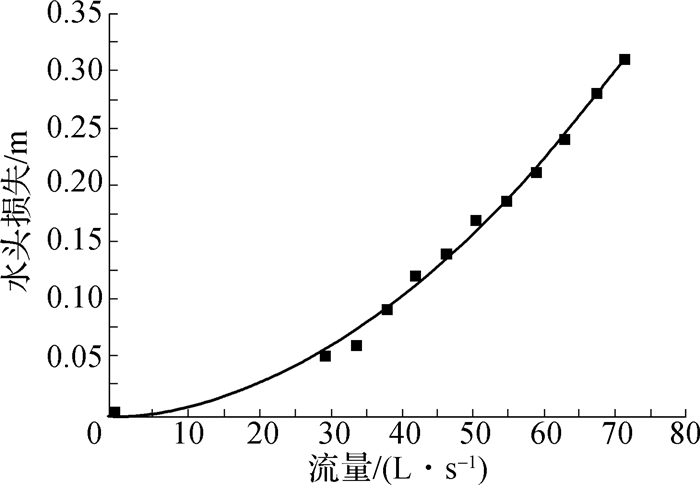
2.2 试验结果及分析采用出水流道模型试验的方法对虹吸式出水流道水头损失进行测试和计算,得到了不同流量时的虹吸式出水流道水头损失(图 2中的点),并将各点数据进行拟合得到了流量-水头损失关系曲线(见图 2)。试验结果表明在设计流量下该流道的水头损失Δh为0.310 m。

|
图 2 虹吸式出水流道水头损失测试结果 Fig.2 Head loss curves for siphon outlet conduit |
试验中对虹吸式出水流道模型内的水流流态进行了观察和记录,流态见图 3。由流道出口向进口方向观察,可以看到:受水泵出口水流旋转影响,水流沿顺时针方向旋转流进出水流道; 流道上升段内,受旋转水流影响,流道上边壁丝线向水流流动的左前方偏转,下边壁丝线向右前方偏转,右边壁丝线斜向上,左边壁丝线斜向下; 受流道逐渐扩散和转向的影响,水流旋转程度逐渐减弱,出水流道下降段内的水流平顺、扩散平缓,丝线偏向与倾角较小,基本沿流道壁面延伸方向运动; 受流道转向影响,驼峰顶外侧存在低速区,丝线摆动幅度较大、频率低; 受水流旋转和运动惯性的共同影响,流道下降段顶部流速大于底部,流道出口底部左侧流速高于右侧,表现为左侧丝线摆动频率高、右侧丝线摆动频率低; 该虹吸式出水流道内的水流均匀扩散、有序转向,整个流道内无旋涡产生。
|
图 3 虹吸式出水流道流态照片 Fig.3 Flow patterns in siphon outlet conduit |
虹吸式出水流道内的三维湍流的流动可用连续方程和Navier-Stokes方程(N-S方程)描述,其微分张量形式为:
| $ {\partial \rho /\partial t + \partial \left( {\rho {u_i}} \right)/\partial {x_i} = 0} $ | (1) |
| $ {\partial \left( {\rho {u_i}} \right)/\partial t + \partial \left( {\rho {u_i}{u_j}} \right)/\partial {x_j} = \partial P/\partial {x_i} + \partial \left[ {\mu \left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right)} \right]/\partial {x_i} + \rho {f_i}} $ | (2) |
式中:ρ为流体密度; ui,uj为分别与坐标轴xi和xj平行的速度分量; P为压力; t为时间; μ为流体动力黏度; fi为体积力。
虹吸式出水流道内部流动为复杂的三维湍流流动,其运动可视为流动平均值与脉动值的叠加。目前工程上一般对N-S方程进行时均化处理,采用雷诺时均N-S方程,其张量形式表达为:
| $ {\partial \left( {\rho \overline {{u_i}} } \right)/\partial t + \partial \left( {\rho \overline {{u_i}} \overline {{u_j}} } \right)/\partial {x_j} = \partial \bar P/\partial {x_i} + \partial \left( {\mu \frac{{\partial \overline {{u_i}} }}{{\partial {x_j}}} - \rho {{\overline {{{u'}_i}u'} }_j}} \right)/\partial {x_i} + \rho {f_i}} $ | (3) |
式中:
为使求解各流体流动参数的方程组封闭,还需引入湍流模型。应用于低扬程泵站出水流道水力性能数值模拟的湍流模型有多种,选择了常用的一方程模型(如S-A模型)、二方程模型(如k-ε模型、k-ω模型)及Reynolds Stress模型分别对虹吸式出水流道水力性能进行三维湍流流动数值模拟。
3.2 边界条件及计算设置为满足设置流场计算进口边界的条件,将虹吸式出水流道进口逆水流方向等直径延伸形成进水直管,延伸长度为流道进口直径的两倍,将流场计算进口边界设置在进水直管的进口断面,可认为该处来流均匀,因单泵设计流量已知,故采用速度进口边界条件。由于出水流道进口与水泵导叶体出口连接,流出导叶体的水流仍具有一定剩余环量[12],故还需在此设置一定环量。出水流道出口连接泵站出水池,将流场计算出口边界设置在出水池中距离流道出口断面足够远的地方,该处的水流流动充分发展,采用自由出流边界条件。进水直管边壁、流道边壁和出水池底壁均采用固壁边界,采用固壁定律进行处理。出水池的表面为自由水面,不计大气交换和忽略外界流动造成的相关力影响,可视为对称平面处理[13]。出水流道流场数值模拟的计算为定常计算,压力速度耦合采用SIMPLEC算法,计算收敛精度设置为10-6。
3.3 网格剖分及无关性分析网格类型及数量直接影响流道流场数值计算的效率与结果的准确性。采用非结构化网格剖分三维形体及流动较为复杂的虹吸式出水流道,采用结构化网格剖分三维形体及流动简单的进水直管段和出水池部分。出水流道计算区域及其网格剖分情况如图 4所示。

|
图 4 出水流道计算区域及网格剖分 Fig.4 Calculation area of outlet conduit and its mesh generation |
为保证虹吸式出水流道水力性能计算结果的精度和计算效率,在网格剖分质量满足要求的情况下,对虹吸式出水流道流场模拟进行网格无关性分析,并采用流道水头损失衡量网格数量对计算结果的影响。选择S-A VBP,S-A SBP,Standard k-ε,RNG k-ε,Realizable k-ε,Standard k-ω,SST k-ω和Reynolds Stress等几种常用湍流模型对不同网格数时的虹吸式出水流道流场进行三维湍流流动数值模拟,计算得到的流道水头损失列于表 1。可以看到:计算区域网格数量明显影响出水流道水头损失数值计算的结果,流道水头损失随网格数量的增加逐渐减小并最终趋于某一值; 不同湍流模型对网格无关性要求不同,所对应的网格数量不同; 对于所选的8种湍流模型,当网格数量达到33.7万后,水头损失计算结果的变化幅度均不超过1%。网格数大于33.7万后,网格数量的增大,不会影响数值计算结果,但会增加计算时间,降低数值计算效率; 为保证不同湍流模型时的计算结果均不受网格影响,对虹吸式出水流道数值计算选择了足够多的网格数,根据网格无关性计算分析结果将网格数定为33.7万。
| 表 1 不同网格数量时的虹吸式出水流道水头损失计算结果 Tab.1 Calculation results of head loss for siphon outlet conduit under different grid numbers |
为了研究不同湍流模型时虹吸式出水流道水头损失计算结果的准确性,将计算结果与模型试验结果比较,分析各个湍流模型下计算结果的相对误差:
| $ {E_{\rm{H}}} = \left( {{H_{{\rm{NC}}}} - {H_{{\rm{EX}}}}} \right)/{H_{{\rm{EX}}}} \times 100\% $ | (4) |
式中:EH为流道水头损失计算的相对误差; HNC为数值计算的流道水头损失; HEX为模型试验的流道水头损失。
采用三维湍流流动数值模拟方法,对采用S-A VBP,S-A SBP, Standard k-ε, RNG k-ε, Realizable k-ε, Standard k-ω, SST k-ω和Reynolds Stress湍流模型时虹吸式出水流道水头损失分别进行了数值模拟,计算得到的设计流量时虹吸式出水流道水头损失列于表 2,并根据式(4)计算流道水头损失数值计算结果的相对误差。
| 表 2 不同湍流模型时的虹吸式出水流道水头损失 Tab.2 Head loss of siphon outlet conduit in different turbulence models |
由表 2可见:S-A VBP湍流模型和S-A SBP湍流模型计算得到的水头损失误差较大,其相对误差均超过了8%,原因在于一方程湍流忽略了剪切层厚度,无法处理边界处黏性影响区域,造成了水头损失计算值小、相对误差较大[14]; Reynolds Stress湍流模型计算得到的流道水头损失值最小,相对误差最大; 两方程湍流模型中,RNG k -ε模型能够很好地处理高应变率及流线弯曲程度较大的流动[14],但是虹吸式出水流道内的水流并未达到该湍流模型的要求,因此计算结果相对误差略大; 除RNG k-ε湍流模型外常用的两方程模型在虹吸式出水流道水头损失的计算结果中展现了优越的适用性,Standard k-ε,Realizable k-ε与SST k-ω等3种湍流模型数值计算得到的水头损失相对误差均小于3%。
4.2 三维流场计算结果及分析基于表 2中水头损失计算相对误差较小的Standard k-ε,Realizable k-ε与SST k-ω等3种湍流模型对虹吸式出水流道流场进行数值模拟,计算得到设计流量时的流道表面流场见图 5。

|
图 5 不同湍流模型下的虹吸式出水流道流场 Fig.5 Flow field of siphon outlet conduit in different turbulence models |
从流场图可见:受出水流道进口水流环量影响,水流以螺旋状进入出水流道,水流在出水流道内边转向、边旋转、边扩散,旋转程度由进口至出口逐渐减弱,转向处内侧流速大于外侧; 采用Standard k-ε湍流模型时,出水流道内的水流转向有序、扩散平稳均匀,在水流运动惯性与环量共同作用下,靠近流道出口的底部右侧区域存在局部低速区,整个流道内流态很好,无旋涡等不良流态; 采用Realizable k-ε湍流模型时,在流道上升段右下侧存在条状低速区,在流道下降段右侧底部存在较大范围旋涡区; 采用SST k-ω湍流模型时的出水流场与采用Realizable k-ε湍流模型时的基本相同,前者下降段的旋涡区范围略大。
将数值计算得到的虹吸式出水流道流场(图 5)与透明流道模型试验的出水流态(图 4)比较可知,采用Standard k-ε湍流模型时的流场计算结果与模型试验结果最吻合。
5 结语(1) 大型低扬程泵站中,在水泵导叶体出口水流环量的作用下,水流旋转进入出水流道,水流在虹吸式出水流道内作边转向、边旋转和边扩散的流动,水流旋转强度从流道进口至出口逐渐减弱。
(2) 与一方程湍流模型和Reynolds Stress湍流模型相比,二方程湍流模型在虹吸式出水流道水头损失计算中具有优越性; 与虹吸式出水流道模型试验结果相比,采用Standard k-ε,Realizable k-ε和SST k-ω等3种二方程湍流模型计算得到的水头损失相对误差小于3%。
(3) 与虹吸式出水流道模型试验中观察的流态相比,在水头损失计算相对误差较小的Standard k-ε,Realizable k-ε和SST k-ω等3种湍流模型中,采用Standard k-ε湍流模型计算的流场与流道模型试验结果最吻合。
| [1] |
陆林广, 杲东彦, 祝婕. 大型泵站虹吸式出水流道优化水力设计[J]. 农业机械学报, 2005, 36(4): 60-63. ( LU Linguang, GAO Dongyan, ZHU Jie. Optimized hydraulic design of siphon outlet in large pumping stations[J]. Transactions of the Chinese Society of Agricultural Machinery, 2005, 36(4): 60-63. DOI:10.3969/j.issn.1000-1298.2005.04.016 (in Chinese)) |
| [2] |
徐磊, 陆林广, 梁金栋, 等. 低扬程泵装置优化水力设计的关键问题[J]. 水利水运工程学报, 2012(2): 62-70. ( XU Lei, LU Linguang, LIANG Jindong, et al. A study of the key problem of optimum hydraulic design for a pump system with low head[J]. Hydro-Science and Engineering, 2012(2): 62-70. DOI:10.3969/j.issn.1009-640X.2012.02.010 (in Chinese)) |
| [3] |
丁军, 丁庆朋. 胥浦活水泵站肘形进水流道流态分析及优化[J]. 水利水运工程学报, 2015(3): 88-94. ( DING Jun, DING Qingpeng. Flow pattern analysis and optimization of elbow inlet conduits in Xupu running water pumping station[J]. Hydro-Science and Engineering, 2015(3): 88-94. (in Chinese)) |
| [4] |
徐磊, 陆林广, 王海, 等. 竖井式进水流道尺寸对水力性能的影响[J]. 水利水运工程学报, 2014(5): 47-52. ( XU Lei, LU Linguang, WANG Hai, et al. Influence of control size on shaft inlet conduit on hydraulic performance[J]. Hydro-Science and Engineering, 2014(5): 47-52. DOI:10.3969/j.issn.1009-640X.2014.05.008 (in Chinese)) |
| [5] |
王福军. 流体机械旋转湍流计算模型研究进展[J]. 农业机械学报, 2016, 47(2): 1-14. ( WANG Fujun. Research progress of computational model for rotating turbulent flow in fluid machinery[J]. Transactions of the Chinese Society of Agricultural Machinery, 2016, 47(2): 1-14. (in Chinese)) |
| [6] |
张德胜, 施卫东, 张华, 等. 不同湍流模型在轴流泵性能预测中的应用[J]. 农业工程学报, 2012, 28(1): 66-71. ( ZHANG Desheng, SHI Weidong, ZHANG Hua, et al. Application of different turbulence models for predicting performance of axial flow pump[J]. Transactions of the Chinese Society of Agricultural Engineering, 2012, 28(1): 66-71. DOI:10.3969/j.issn.1002-6819.2012.01.013 (in Chinese)) |
| [7] |
张淑佳, 李贤华, 朱保林, 等. k-ε涡粘湍流模型用于离心泵数值模拟的适用性[J]. 机械工程学报, 2009, 45(4): 238-242. ( ZHANG Shujia, LI Xianhua, ZHU Baolin, et al. Applicability of k-ε eddy viscosity turbulence models on numerical simulation of centrifugal pump[J]. Journal of Mechanical Engineering, 2009, 45(4): 238-242. (in Chinese)) |
| [8] |
丛国辉, 王福军. 湍流模型在泵站进水池漩涡模拟中的适用性研究[J]. 农业工程学报, 2008, 24(6): 31-35. ( CONG Guohui, WANG Fujun. Applicability of turbulence models in numerical simulation of vortex flow in pump sump[J]. Transactions of the Chinese Society of Agricultural Engineering, 2008, 24(6): 31-35. (in Chinese)) |
| [9] |
印超.泵站前池流态改善三维数值模拟研究[D].扬州: 扬州大学, 2007. (YIN Chao. Three-dimensional numerical simulation study on flow state improvement of pump station forebay[D]. Yangzhou: Yangzhou University, 2007. (in Chinese)) http://cdmd.cnki.com.cn/Article/CDMD-11117-2007149486.htm
|
| [10] |
祝婕.宝应泵站进出水流道优化水力设计及模型试验研究[D].扬州: 扬州大学, 2005. (ZHU Jie. Optimized hydraulic design and model test study of inlet and outlet conduit of Baoying pump station[D]. Yangzhou: Yangzhou University, 2005. (in Chinese)) http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y748094
|
| [11] |
陆林广, 吴开平, 冷豫, 等. 泵站出水流道模型水力损失的测试[J]. 排灌机械, 2005, 23(5): 23-26. ( LU Linguang, WU Kaiping, LENG Yu, et al. Measurement for hydraulic loss of outlet conduit of pumping station[J]. Journal of Drainage and Irrigation Machinery Engineering, 2005, 23(5): 23-26. DOI:10.3969/j.issn.1674-8530.2005.05.005 (in Chinese)) |
| [12] |
梁金栋.低扬程立式泵装置优化水力设计研究[D].扬州: 扬州大学, 2012. (LIANG Jindong. Optimization of hydraulic design for low head vertical pump device[D]. Yangzhou: Yangzhou University, 2012. (in Chinese))
|
| [13] |
CHEN H X, GUO J H. Numerical simulation of 3-D turbulent flow in the multi-intakes sump of the pump station[J]. Journal of Hydrodynamics(Ser B), 2007, 19(1): 42-47. DOI:10.1016/S1001-6058(07)60026-2 |
| [14] |
王福军. 计算流体动力学分析[M]. 北京: 清华大学出版社, 2004. ( WANG Fujun. Computational fluid dynamics analysis[M]. Beijing: Tsinghua University Press, 2004. (in Chinese))
|
2. The Eastern Route of South-to-North Water Diversion Project Jiangsu Water Source Co., Ltd., Nanjing 210019, China;
3. Institute of Water Conservancy Works Design of Xuzhou, Xuzhou 221000, China
 2019
2019 