2. 河海大学 港口海岸与近海工程学院,江苏 南京 210098;
3. 杰克逊州立大学 土木与环境工程系,密西西比 杰克逊 39217
波浪溢流指强风暴潮时海堤堤前水位超过堤顶,海堤受到的越浪与溢流联合作用[1-2]。在全球气候变暖的背景下,沿海地区极端高水位和热带气旋最大风速都在增加[3],波浪溢流的发生概率上升,并引发了数起严重的溃堤事件。如1953年发生的一场特大风暴潮在英国东海岸造成了1 200处溃堤,导致英国和荷兰死亡人数超过2 000人[4]; 2005年的卡特里娜飓风风暴潮期间,美国墨西哥湾沿岸海堤共发生了50处溃堤,其中43处由波浪溢流对海堤内坡的侵蚀所致[5]; 2013年在广东汕尾登陆的“天兔”台风期间,饶平小红山段约4 km长的海堤发生了4处溃堤,都是波浪溢流作用下海堤内坡侵蚀导致防浪墙失去支撑的结果。因此,研究波浪溢流期间海堤内坡水动力特征对海岸防灾具有重要意义。
在2005年的卡特里娜飓风后,波浪溢流致灾得到了海岸工程界的高度重视,而早期的研究重点在波浪溢流量。波浪溢流量指波浪溢流引起的平均单宽越堤流量,是用来表征波浪溢流的重要水力学参数。较早的应急性公式在欧洲的越浪手册[6]中给出,将溢流产生的稳定流量和海堤出水高度为零时的越浪量线性叠加得到波浪溢流引起的越堤流量。Reeve等[7]基于雷诺平均N-S方程建立了数值水槽,用以研究不可渗透海堤的波浪溢流量,给出了上游水位较低时无量纲波浪溢流量的表达式,但与后续水槽试验结果比较,他们的计算式过高估计了波浪溢流量。Hughes等[8]对波浪溢流进行了一系列25:1的水槽试验研究,给出了估算无量纲平均波浪溢流量的经验公式,也对内坡水动力条件进行了初步探讨,但其研究主要为降比尺的试验研究,未考虑不同海堤护坡的影响。
为研究不同海堤内坡护坡条件下波浪溢流的水力学参数和护坡侵蚀特征,Pan等[9]在美国俄勒冈州立大学进行了比尺为1:1的大型水槽试验,试验期间在海堤模型内坡铺设了3种不同的护坡材料,包括碾压混凝土、铰接式护坡砖和高性能加筋草皮。这3种护坡材料是堤防护坡常用材料,抗侵蚀能力由强到弱,生态性由弱到强。本文以大型水槽试验结果为基础,以波浪溢流过程中内坡水动力特征为研究对象,探讨波浪溢流过程中不同海堤内坡护坡条件下内坡上的平均水深和流速、波高和峰值水深分布、特征波高和平均波速等水力学参数的特征,并给出经验式,试验研究结果可为波浪溢流期间海堤内坡防御的相关研究提供参考。
1 大型水槽试验及内坡护坡简介波浪溢流大型水槽试验在美国俄勒冈州立大学欣斯代尔波浪研究实验室的大水槽进行。该水槽长104 m,宽3.7 m,高4.6 m,配有活塞式造波机,可由给定谱生成随机波。海堤模型比尺为1:1,如图 1所示。海堤模型距造波机44.28 m,海堤高度为3.25 m,外坡坡度为1:4.25,内坡坡度为1:3。海堤模型上游装有4个电容式波高仪,波高仪2~4作为1个三波高仪阵列,使用文献[10]的方法进行波浪的入反射分离,波高仪1作为备用。在波高仪3和4之间安装1个超声波水位仪,用以校正波高仪的读数。

|
图 1 大水槽和海堤模型(单位:m) Fig.1 Large flume and seawall model (unit:m) |
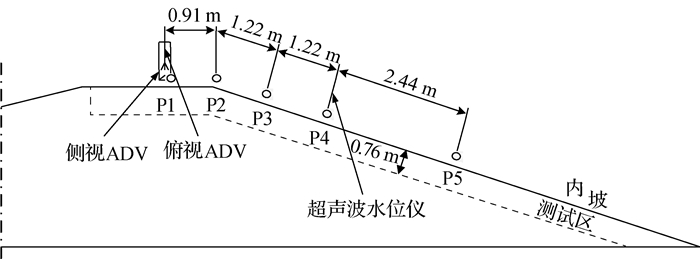
在海堤模型内部留有深0.76 m,宽2.34 m的测试区,用来安置3种海堤内坡护坡,如图 2所示。使用多普勒流速仪(ADV)测量海堤堤顶和内坡流速。如图 2所示的P1点分别放置1台俯视ADV和1台侧视ADV。俯视ADV探头安置在距海堤模型表面8 cm处,测量距海堤模型表面3 cm处的流速; 侧视ADV探头安置在距海堤模型表面0.5 cm处,测量距海堤模型表面0.5 cm处的流速。如图 2所示的P1~P5点安装超声波水位仪测量水位。
|
图 2 水力学数据测点布置 Fig.2 Layout of measuring points for obtaining hydraulic data |
在图 1所示的测试区内部,不同试验组次中依次采用不同类型的海堤护坡,包括碾压混凝土、铰接式护坡砖和高性能加筋草皮。3种海堤内坡护坡如图 3所示。碾压混凝土是一种干硬性贫水泥混凝土,使用硅酸盐水泥、火山灰质掺和料、水、砂和分级控制的粗骨料拌制成无塌落度的干硬性混凝土,用振动碾分层压实。铰接式护坡砖是一种连锁型预制高强混凝土块,砖块之间靠砖块边缘的突起进行咬合,并在内部预留有前后贯穿的孔洞,可使用钢缆连接以增加护坡系统抵御大浪的能力。护坡砖中部留有上下联通的植被开孔,可种植植被以增加护坡的生态功能。加筋草皮是使用生态加筋网加固的草皮; 生态加筋网在培植草皮前被预置于土壤中,在植被生长过程中草根茎穿过生态加筋网生长,使土壤、植被、生态加筋网三者紧密结合在一起[11],加筋草皮的抗水流冲刷能力可达到普通草皮的数倍[12]。

|
图 3 3种海堤内坡护坡材料 Fig.3 Three kinds of slope protection materials for inner slope of seawall |
共进行了24组不同有效波高(Hm0)、谱峰周期(Tp)和海堤出水高度(Rc)组合下的波浪溢流试验,包括11组碾压混凝土试验、4组铰接式护坡砖试验和9组高性能加筋草皮试验,具体试验组次见表 1。波浪溢流试验中的波浪序列根据TMA谱(Texel-Marsden-Arsloe谱,一种改进的JONSWAP谱,更适用于过渡水深的情形)生成。
| 表 1 试验组次 Tab.1 Test groups |
波浪溢流为非恒定流,但类似于溢流,其内坡上的水流统计学参数(如平均水深、平均流速、特征波高等)在下降一定高度后基本保持稳定,可以认为此时越堤水流处于稳定状态,其统计学特征参数沿海堤内坡向下不再变化。观测数据表明,P4和P5点的平均流速与平均水位非常接近,可以认为在P4点处内坡水流的统计学参数已处于基本稳定状态; 另一方面,通常认为流速越大的水流对护坡的侵蚀越明显,因此可以认为P4~P5稳定段比P2~P4过渡段动力条件更危险,故选取稳定段的水力学参数作为研究对象。本研究中内坡上的水力学参数根据P4,P5测点超声波水位仪的测量结果计算得到。此外,波浪溢流引起的越堤流量过程由堤顶上P1点的2台ADV和1台超声波水位仪测得的流速与水位时间序列计算得到,将计算所得越堤流量过程取均值得到平均(单宽)波浪溢流量(简称波浪溢流量,qws)和P4,P5点的水位数据一起用于估算内坡水力学参数。
2 内坡平均水深和平均流速计算位于内坡中部P5测点处水深时间序列的均值为内坡平均水深dm。经过与不同特征参数的组合分析,在内坡平均水深dm与波浪溢流量qws之间建立相关关系,如图 4所示。图中直线为拟合曲线,可表示为:

|
图 4 内坡平均水深和波浪溢流量之间关系 Fig.4 Relationship curves between average water depth along landside and wave overflow discharge |
| $ q_{\mathrm{ws}} / \sqrt{g d_{\mathrm{m}}^{3}}=k_{\mathrm{dm}} $ | (1) |
式中:dm为内坡平均水深; kdm为波浪溢流内坡平均水深相关的经验参数,对于碾压混凝土、铰接式护坡砖和高性能加筋草皮分别取4.811,2.907和2.362。
如果内坡平均流速vm定义为波浪溢流量qws除以内坡平均水深dm,那么内坡平均流速vm可以写成:
| $ v_{\mathrm{m}}=k_{\mathrm{dm}} \sqrt{g d_{\mathrm{m}}} $ | (2) |
可见式(2)的形式与谢才公式类似。无限宽明渠恒定流(摩阻比降与坡度相等)的谢才公式可以写成:
| $ v = \sqrt {2\sin \theta /{f_{\rm{F}}}} \sqrt {gd} $ | (3) |
式中:θ为坡角; fF为范宁摩擦因数; d为水深。为了考虑坡度和底摩阻的影响,这里借用谢才公式的形式,令两个公式中的系数相等,并使用内坡坡角β代替式(3)中的坡角θ,即
| $ k_{\mathrm{dm}}=\sqrt{2 \sin \beta / f_{\mathrm{F}}} $ | (4) |
已知内坡坡度为1:3,可以解出碾压混凝土、铰接式护坡砖和高性能加筋草皮的范宁摩擦因数fF分别为0.027 3,0.074 8和0.113 4。要注意这里的波浪溢流并非恒定流,故严格意义上讲,这里解出的fF并非真正意义上的范宁摩擦因数,因此在下文中用等价范宁摩擦因数fF*来替代。至此,考虑坡度和底摩阻影响的内坡平均水深dm可通过下式计算
| $ {{d_{\rm{m}}} = {{\left( {\frac{{q_{{\rm{ws}}}^2{f_{{{\rm{F}}^{\rm{*}}}}}}}{{2g\sin \beta }}} \right)}^{1/3}}} $ | (5) |
内坡平均流速vm可通过下式计算
| $ {{v_{\rm{m}}} = {{\left( {\frac{{2{q_{{\rm{ws}}}}g\sin \beta }}{{{f_{{{\rm{F}}^{\rm{*}}}}}}}} \right)}^{1/3}}} $ | (6) |
需要注意的是,这里的式(5)和(6)是试探性的拓展,其适用性还需更多试验或现场数据予以支持。式(5)和(6)的适用范围为0<qws<0.34 m3/s/m,对于波浪溢流量超出此范围的动力条件和内坡坡度不为1:3的海堤应慎用。
3 内坡波高和峰值水深分布特征对所有波浪溢流试验组次在P4点的水深时间序列采用上跨零点法进行分析,计算内坡上每一个波浪对应的特征波高,包括均方根波高(Hrms)、有效波高(H1/3)、显著波高(H1/10)和百分之一大波波高(H1/100)。为了检验海堤内坡上的波高分布是否仍符合瑞利分布,根据瑞利分布公式使用均方根波高(Hrms)对有效波高(H1/3)、显著波高(H1/10)和百分之一大波波高(H1/100)进行计算,并对计算值和实测值进行比较。瑞利分布表示的各种特征波高之间关系可写为:
| $ {H_{1/3}} = 1.416{H_{{\rm{rms}}}};{H_{1/10}} = 1.80{H_{{\rm{rms}}}};{H_{1/100}} = 2.36{H_{{\rm{rms}}}} $ | (7) |
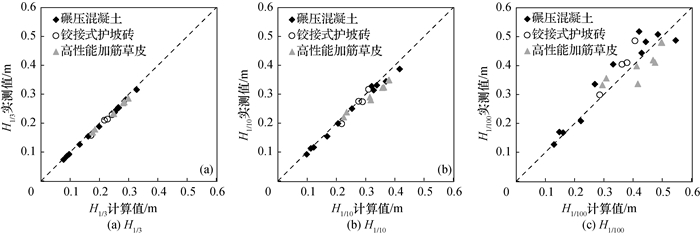
3种特征波高的计算值和实测值比较绘于图 5。如图所示,H1/3和H1/10的计算值和实测值拟合非常好。H1/100的拟合相对离散,导致这一现象的原因可能是试验历时较短,没有足够的波浪样本来计算H1/100; 虽然如此,瑞利分布对H1/100的计算仍处于合理范围。因此,可以认为波浪溢流过程中海堤内坡上的波高分布仍符合瑞利分布,可以根据瑞利分布,通过某一特征波高计算其他特征波高的数值。
|
图 5 海堤内坡特征波高计算值与实测值比较 Fig.5 Comparison between calculated and measured values of characteristic wave height along landside |
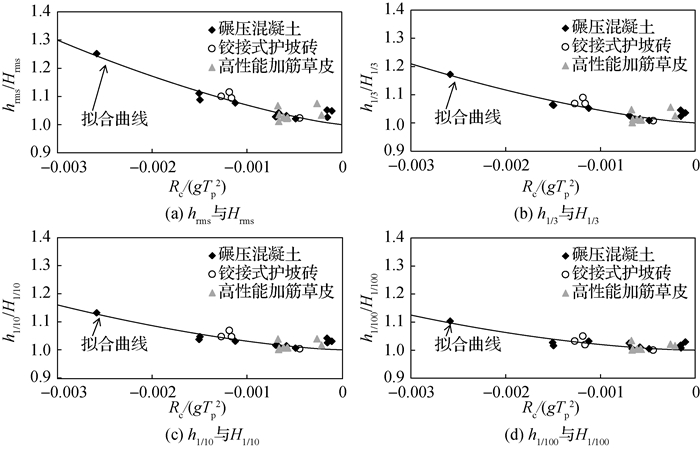
虽然波浪溢流在海堤内坡上的时空变化可用波高分布来描述,但对于海堤内坡防护来说,更关注的可能是波浪引起的峰值水深而非波高本身。海堤内坡上波高呈现很好的瑞利分布,则以方便得到的特征波高来表征对应的特征峰值水深。对P4点的水深时间序列进行上跨零点法分析,分辨每一个波浪过程的峰值水深,并对所有峰值水深进行统计分析,可以得到均方根峰值水深(hrms)、三分之一峰值水深(h1/3)、十分之一峰值水深(h1/10)和百分之一峰值水深(h1/100)。注意,这里的h是指峰值水深而非一般水深,即每一个波浪只对应一个峰值水深。经多次尝试,选择以无量纲参数(Rc/(gTp2))来表征特征峰值水深与对应的特征波高之间的关系。图 6给出了4种特征峰值水深与对应特征波高的比值与无量纲参数(Rc/(gTp2))的关系。如图所示,当无量纲参数(Rc/(gTp2))越接近0时,特征峰值水深与对应的特征波高的比值越接近1,说明在更多的相邻波浪之间会发生“断流”(即波谷水深为0);无量纲参数(Rc/(gTp2))为0时,特征峰值与特征波高相等,波浪溢流退化为越浪。此外,不同的海堤内坡护坡方式对数据分布趋势的影响不大。图 6中曲线为4种特征峰值水深与对应特征波高比值关系的拟合曲线,对应的经验公式为:
|
图 6 海堤内坡特征峰值水深与特征波高之间关系 Fig.6 Relationships between characteristic peak water depth and characteristic wave height |
| $ {\frac{{{h_{{\rm{rms}}}}}}{{{H_{{\rm{rms}}}}}} = \exp \left[ {350.2{{\left( { - \frac{{{R_{\rm{c}}}}}{{gT_{\rm{p}}^2}}} \right)}^{1.239}}} \right]} $ | (8) |
| $ {\frac{{{h_{1/3}}}}{{{H_{1/3}}}} = \exp \left[ {462.6{{\left( { - \frac{{{R_{\rm{c}}}}}{{gT_{\rm{p}}^2}}} \right)}^{1.342}}} \right]} $ | (9) |
| $ {\frac{{{h_{1/10}}}}{{{H_{1/10}}}} = \exp \left[ {645.3{{\left( { - \frac{{{R_{\rm{c}}}}}{{gT_{\rm{p}}^2}}} \right)}^{1.442}}} \right]} $ | (10) |
| $ {\frac{{{h_{1/100}}}}{{{H_{1/100}}}} = \exp \left[ {1431{{\left( { - \frac{{{R_{\rm{c}}}}}{{gT_{\rm{p}}^2}}} \right)}^{1.619}}} \right]} $ | (11) |
式(8)~(11)的可决系数R2分别为0.784 5,0.703 2,0.637 6和0.637 2,均方根误差分别为0.024 1,0.021 0,0.017 65和0.013 66。可通过式(8)~(11)对波浪溢流过程中海堤内坡上的特征峰值水深进行预测。式(8)~(11)的适用范围为-0.35 m<Rc<0,3.3 s<Tp<7.7 s,对于参数超出此范围的动力条件和内坡坡度不为1:3的海堤应慎用。
4 内坡均方根波高由上节可知,波浪溢流过程中海堤内坡上的波高呈较好的瑞利分布,且特征峰值水深与对应的特征波高之间能建立经验关系; 那么,如果有了内坡上的均方根波高Hrms,就可以计算出内坡上的各种特征波高和各种特征峰值水深的值。
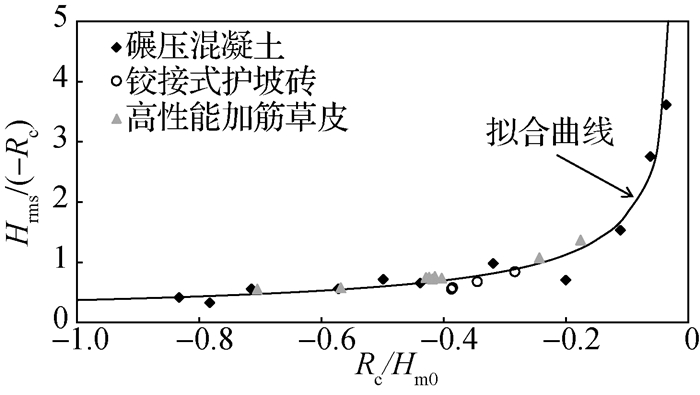
经多次尝试,选择以无量纲参数Hrms/(-Rc)与海堤相对出水高度Rc/Hm0之间的关系来估算内坡均方根波高Hrms的数值。图 7给出了无量纲参数Hrms/(-Rc)与海堤相对出水高度Rc/Hm0之间的关系。如图 7所示,3种海堤内坡护坡方式组次的数据表现出较为一致的分布趋势。图中拟合曲线对应的经验式为:
|
图 7 海堤内坡上均方根波高的估算 Fig.7 Estimation of Hrms on landside of seawall |
| $ \frac{H_{\mathrm{rms}}}{-R_{\mathrm{c}}}=0.371\left(-\frac{R_{\mathrm{c}}}{H_{\mathrm{m} 0}}\right)^{0.69} $ | (12) |
式(12)的可决系数R2为0.967,均方根误差为0.136 4,适用范围为-0.35 m<Rc<0,3.3 s<Tp<7.7 s,对于参数超出此范围的动力条件和内坡坡度不为1:3的海堤应慎用。
5 内坡平均波速海堤内坡上的波速可根据相邻测点测得的水深时间序列来获取。根据每个波形在P4,P5点之间移动所需的时间和测点之间的距离计算每个单独波浪的波速,取平均值得到内坡上的平均波速。经多次尝试,选择以水力学参数(gqws)1/3来表征内坡平均波速vw的数值。将试验测得的内坡平均波速vw及水力学参数(gqws)1/3绘制于图 8,可以看出二者呈线性相关关系,且不同的海堤内坡护坡方式对数据分布趋势的影响不大。图中拟合曲线对应的经验式为:

|
图 8 海堤内坡平均波速估算 Fig.8 Estimation of average wave velocity on landside of seawall |
| $ {v_{\rm{w}}} = 4.325{\left( {g{q_{{\rm{ws}}}}} \right)^{1/3}} $ | (13) |
式(13)的可决系数R2为0.640 8,均方根误差为0.406 8,适用范围为0<qws<0.34 m3/s/m,对于波浪溢流量超出此范围的动力条件和内坡坡度不为1:3的海堤应慎用。
6 结语基于1:1的大型水槽试验研究,分析了波浪溢流过程中不同海堤内坡护坡条件下海堤内坡的水力学特征。共进行了3种内坡护坡(碾压混凝土、铰接式护坡砖和高性能加筋草皮)条件下的24组波浪溢流水槽试验,记录了海堤模型堤顶和内坡5个测点处的水位和流速数据。通过对试验结果进行分析,建立了波浪溢流过程中不同海堤内坡护坡条件下内坡平均水深和平均流速的计算方法; 证明了波浪溢流过程中海堤内坡上波高分布仍符合瑞利分布,在此基础上建立了内坡上特征波高和特征峰值水深之间的换算关系; 提出了波浪溢流过程中海堤内坡上均方根波高的计算方法,以此为基础可计算海堤内坡上的其他特征波高和特征峰值水深; 给出了波浪溢流过程中海堤内坡波速的经验计算式。
试验研究结果可为分析研究波浪溢流期间海堤内坡的防御,以及海堤的设计、评估和加固提供相关技术参考和依据。
| [1] |
HUGHES S A. Levee overtopping design guidance: what we know and what we need[C]//Proc of the solutions to coastal disasters congress, Turtle Bay, HI, 2008: 867-880.
|
| [2] |
潘毅.海岸防护——人工养滩工程和海堤越浪、溢流和加固的研究[D].上海: 同济大学, 2012. (PAN Yi. Coastal protection: studies on beach nourishment and the strengthening of levee against surge and wave overtopping[D]. Shanghai: Tongji University, 2012. (in Chinese))
|
| [3] |
IPCC. Managing the risks of extreme events and disasters to advance climate change adaptation: a special report of working groups Ⅰ and Ⅱ of the intergovernmental panel on climate change[M]. Cambridge: Cambridge University Press, 2012: 582.
|
| [4] |
BAXTER P J. The east coast big flood, 31 January-1 February 1953: a summary of the human disaster[J]. Philosophical Transactions of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, 2005, 363: 1293-1312. DOI:10.1098/rsta.2005.1569 |
| [5] |
ASCE Hurricane Katrina External Review Panel. The New Orleans hurricane protection system: what went wrong and why[M]. Reston: ASCE, 2007: 92.
|
| [6] |
PULLEN T, ALLSOP N W H, BRUCE T, et al. EurOtop: wave overtopping of sea defences and related structures: assessment manual[M]. UK: Environment Agency, 2007.
|
| [7] |
REEVE D E, SOLIMAN A, LIN P Z. Numerical study of combined overflow and wave overtopping over a smooth impermeable seawall[J]. Coastal Engineering, 2008, 55(2): 155-166. |
| [8] |
HUGHES S A, NADAL N C. Laboratory study of combined wave overtopping and storm surge overflow of a levee[J]. Coastal Engineering, 2009, 56(3): 244-259. DOI:10.1016/j.coastaleng.2008.09.005 |
| [9] |
PAN Y, KUANG C P, LI L, et al. Full-scale laboratory study on distribution of individual wave overtopping volumes over a levee under negative freeboard[J]. Coastal Engineering, 2015, 97: 11-20. DOI:10.1016/j.coastaleng.2014.12.007 |
| [10] |
MANSARD E P D, FUNKE E R. The measurement of incident and reflected spectra using a least square method[C]//Conference Information 17th International Conference on Coastal Engineering, Sydney, Australia, 23-28 March 1980: 154-172.
|
| [11] |
张同鑫, 潘毅, 张壮, 等. 加筋生态护坡技术的应用与发展[J]. 水利水运工程学报, 2017(6): 110-117. ( ZHANG Tongxin, PAN Yi, ZHANG Zhuang, et al. Application and development of TRM technology in revetment works[J]. Hydro-Science and Engineering, 2017(6): 110-117. (in Chinese)) |
| [12] |
胡玉植, 潘毅, 陈永平. 海堤背水坡加筋草皮抗冲蚀能力试验研究[J]. 水利水运工程学报, 2016(1): 51-57. ( HU Yuzhi, PAN Yi, CHEN Yongping. Experimental studies on scouring resistance of reinforced turf on land-side slope[J]. Hydro-Science and Engineering, 2016(1): 51-57. (in Chinese)) |
2. College of Harbor, Coastal and Offshore Engineering, Hohai University, Nanjing 210098, China;
3. Department of Civil and Environmental Engineering, Jackson State University, Jackson 39217, America
 2019
2019 