剪切强度是混凝土基本力学性能指标之一,国内外众多学者已经进行了大量的试验和理论分析。张琦等[1]进行了不同强度等级四点加载的等高变宽梁抗剪试验,建立了剪切应力-应变曲线方程及剪切模量的计算式;李平先等[2]利用Z形试件进行了不同冻融循环次数后混凝土剪切强度的试验研究;郭艳华等[3]进行了不同钢纤维掺量混凝土在不同压应力下的压剪破坏试验;王怀亮等[4]研究了二级配碾压混凝土在单轴及多轴应力状态下本体和含层面试件的动态抗剪强度和变形特性;王刚等[5]对3种沥青混凝土在4种不同温度条件下的抗剪强度、黏聚力和抗压回弹模量做了试验研究;宋玉普等[6]研究了碾压混凝土在不同侧压应力下的剪切强度;丛宇等[7]通过剪切强度试验,分析了不同强度等级混凝土剪切强度指标黏聚力与内摩擦角的值;郭辉等[8]研究了钢纤维掺量、水灰比及再生粗骨料掺量3个因素对钢纤维再生混凝土抗剪性能的影响。综上所述,目前关于混凝土剪切试验的研究多集中在不同应力状态下不同混凝土的抗剪强度和变形,而关于不同试验因素对混凝土剪切强度影响敏感性、考虑混凝土抗剪速率效应的研究则较少。因此,开展混凝土剪切破坏试验及其试验因素对剪切强度影响的敏感性研究,进一步提高混凝土结构在实际工程应用中的安全性和经济性十分必要。
本文利用大型多功能动静力三轴仪和剪切盒装置进行了混凝土的剪切破坏试验,分析了法向应力、应变速率及冻融循环次数等因素对混凝土剪切强度的影响规律,并利用系统稳定性分析中的敏感性分析方法对以上影响因素进行剪切强度力学参数敏感性分析,确定主要影响因素和次要影响因素,以期为复杂应力状态下混凝土结构设计、混凝土力学性能试验方案设计优化及实际工程结构应用提供参考。
1 敏感性分析方法敏感性分析方法主要用于分析系统的稳定性。敏感性分析的关键工作是通过分析各因素对系统模型的敏感性,得到各因素敏感性系数的大小,然后进行排序,并对不同的影响因素进行敏感性评价。敏感性分析的基本思想是:当进行各试验因素ak对系统特性F的敏感性分析时,令其余试验因素取基准值且数值固定,让试验因素ak在可能变化的范围内浮动,考察试验因素ak的变动对系统特性F的影响程度。如果因素ak微小变化导致系统特性F大幅度波动,则表明系统特性F对因素ak敏感性强,则因素ak是高敏感性因素;反之,系统特性F对因素ak敏感性差,则因素ak是低敏感性因素。
敏感性分析方法目前有多种,参考文献[9],定义无量纲形式敏感性函数:
| $ {S_k}\left( {{a_k}} \right) = (\Delta F/F)/\left( {\Delta {a_k}/{a_k}} \right) = \left| {\Delta F/\Delta {a_k}} \right|\left( {{a_k}/F} \right) $ | (1) |
式中:ak为试验因素,k为因素ak的可能变化范围,k =1, 2, 3,…,n; 当试验中Δak/ak的值很小时,Sk(ak)可近似表达为
由此,绘制出敏感性函数与敏感性因素的曲线Sk(ak)-ak,取ak=ak*,得到该参数无量纲敏感性系数:
| $ S_k^* = {S_k}\left( {a_k^*} \right) = \left| {{{\left( {\frac{{{\rm{d}}{\varphi _k}\left( {{a_k}} \right)}}{{{\rm{d}}{a_k}}}} \right)}_{{a_k} = a_k^*}}} \right|\frac{{a_k^*}}{{{F^*}}} $ | (2) |
通过比较Sk*数值的大小,对系统特性与各试验因素影响的敏感性进行评价,Sk*数值越大,表示系统特性F对因素ak*敏感性越强。
2 剪切强度试验及结果分析 2.1 剪切强度试验按照《水工混凝土配合比设计规程》(DL/T 5330—2015)进行配合比计算,水胶比为0.6,混凝土设计强度为C30,混凝土试件尺寸为300 mm×300 mm×300 mm的立方体,混凝土的原材料组成为:水(175 kg/m3),水泥(291 kg/m3),砂(677 kg/m3),小石(503 kg/m3),中石(754 kg/m3)。剪切试验采用三峡大学与长春朝阳试验仪器有限公司联合研制的大型多功能动静力电液伺服三轴试验机,在此基础上增加一套剪切盒(图 1),该装置能对试件施加水平剪切力。试验时,先将试件装在剪切盒中,然后将剪切盒推入到试验机中,双向施加10 kN的荷载进行预加载并保持恒定,然后按照预定的加载速率在水平方向施加荷载,直至试件剪切破坏。

|
图 1 混凝土剪切试验装置 Fig.1 Concrete shear testing device |
本次试验方案有3种:①混凝土不冻融,竖直方向对试件分别施加轴向法向应力(变化范围为0~35 MPa)并保持恒定,然后水平方向按照应变速率10-5/s加载;②混凝土不冻融,竖直方向不施加轴向法向应力,然后水平方向分别按照应变速率10-5/s,5×10-5/s,10-4/s和10-3/s加载;③混凝土冻融循环0,10,25,35,50次,竖直方向不施加轴向法向应力,然后水平方向按照应变速率10-5/s加载。
混凝土冻融按照《普通混凝土长期性能和耐久性试验方法标准》(GB/T 50082—2009)中抗冻性能试验的“快冻法”进行,冻融循环次数分别为0,10,25,35和50次。
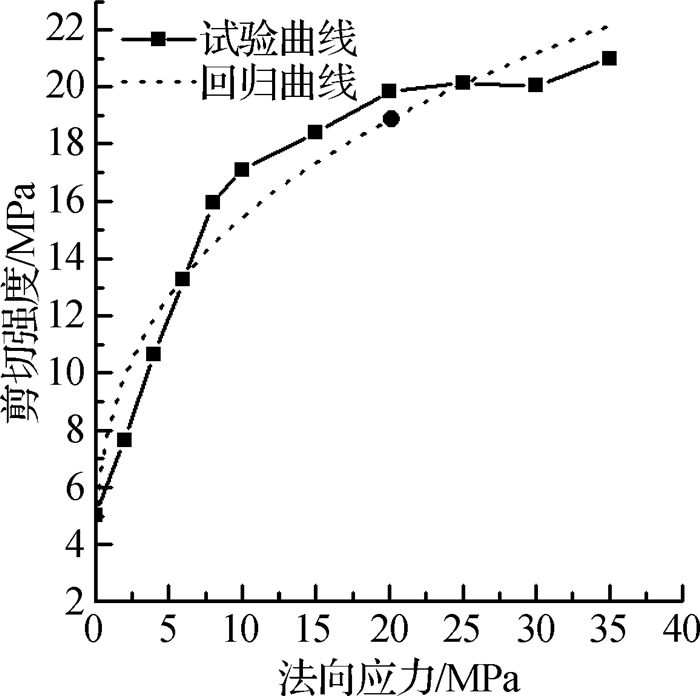
2.2 剪切强度与法向应力的关系在应变速率为10-5/s时,不同法向应力P(变化范围为0~35 MPa)对应的混凝土剪切强度关系见图 2。从图 2可以看出,法向应力在0~35 MPa时,混凝土剪切强度随着法向应力的增大而逐渐提高,剪切强度与法向应力基本呈正相关性。试验曲线分为线性上升段、非线性上升段和稳定段等3个阶段。剪切强度与法向应力的关系采用指数表达式描述:
|
图 2 剪切强度与法向应力的变化规律及回归曲线 Fig.2 Relationships between shear strength and normal stress and its regression curve |
| $ {\varphi _p}(P) = a \times {(P-b)^c} $ | (3) |
式中:φp(P)为剪切强度函数;P为法向应力;a,b,c为回归系数。
利用式(3),对图 2中试验数据进行回归分析,得到剪切强度与法向应力的关系式见式(4),可决系数R2=0.933 5。由回归曲线与试验结果的对比(见图 2)可见,两者吻合程度较好。
| $ {\varphi _p}(P) = 7.842\;14 \times {(P + 0.176\;67)^{0.291\;54}} $ | (4) |
混凝土剪切强度随应变速率的变化规律见图 3。从图 3可以看出,混凝土剪切强度同抗压、抗拉强度一样存在速率效应, 都随应变速率的增加而增大。产生这种规律的原因是:混凝土材料的非均质性和多相性使得混凝土内部微裂缝和孔隙中存在自由水,加载后,混凝土内部微裂缝和孔隙中的自由水相对移动,从而引起会影响混凝土力学性能的类似于流体动力学中Stefan效应的黏滞应力。由文献[10]中牛顿黏性方程式(5)可知,相对移动的液体会引起黏滞剪切应力:

|
图 3 剪切强度与应变速率的变化规律及回归曲线 Fig.3 Relationships between shear strength and strain rate and its regression curve |
| $ {\tau ^\omega } = \frac{F}{A} = \eta \frac{U}{h} = \eta \frac{{{\rm{d}}u}}{{{\rm{d}}y}} $ | (5) |
式中:τω为剪切应力;F为载荷;A为载荷F对应的原始微裂缝的面积;η为水的黏滞系数;U为载荷F引起的加载速度;h为裂缝间距;
根据断裂力学理论,原始微裂缝的滑动速度或裂缝中自由水引起的黏滞应力与加载速度成正比[11-12]。因此,应变速率的增大将引起混凝土中自由水的流动进而导致黏滞阻力增大,从而使混凝土强度提高。
剪切强度与应变速率的关系采用线性表达式描述:
| $ {\varphi _{\dot \varepsilon }}(\dot \varepsilon ) = c + d\dot \varepsilon $ | (6) |
式中:
利用式(6),对试验数据进行回归分析,得到剪切强度与应变速率的关系见式(7),可决系数R2=0.893 0,回归曲线与试验结果的对比见图 3,可见两者吻合程度较好。
| $ {\varphi _{\dot \varepsilon }}(\dot \varepsilon ) = 5.970\;33 + 0.194\;56\;\dot \varepsilon $ | (7) |
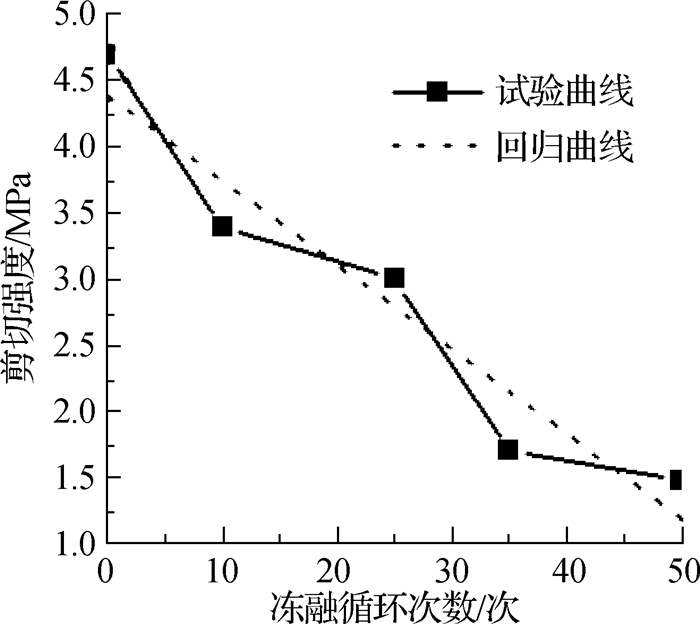
混凝土剪切强度随冻融循环次数的变化规律见图 4,混凝土在历经不同冻融循环次数后外观形态变化见图 5。
|
图 4 剪切强度与冻融循环次数的变化规律及回归曲线 Fig.4 Relationships between shear strength and freeze-thaw cycle times and its regression curve |

|
图 5 不同冻融循环次数后混凝土试件外观形态 Fig.5 Appearance of concrete specimen after different freeze-thaw cycles |
从图 4可以看出,随冻融循环次数的增加,混凝土的剪切强度逐渐降低。这是由于冻结时混凝土试件内部微孔隙中的水会冻结成冰,产生的冻胀力会对微孔隙产生挤压力,导致孔隙逐渐扩展或形成微裂缝;融化时水在混凝土内部微孔隙和微裂缝中移动,对微孔隙和微裂缝产生水压力,进而对孔隙和裂缝间的颗粒造成损坏。由于混凝土材料的不均匀性,在冻融劣化反复作用下,混凝土内部微孔隙急剧增多、裂缝迅速扩展而贯通,从而导致混凝土内部孔隙结构被改变,孔隙率急剧增大,冻融循环作用越多,混凝土孔隙率越大[13-15],混凝土的剪切强度越低,这与文献[16]表明混凝土的强度随孔隙率的增大而降低结论一致。
从图 5可以看出,冻融循环10次后试件外观形态基本没有变化,仅浇筑面出现砂浆层轻微溃散的现象;冻融循环25次后试件部分砂浆开始整体脱落,混凝土试件表面可观察到微裂缝,局部出现麻面;随着冻融循环次数达到35次后试件外观开始出现严重的砂浆脱落,在试件边角处有骨料整体脱落,边角缺失,试件凹凸不平并伴随微裂纹的产生,宏观裂缝形成;而冻融循环50次后破坏程度更为严重,试件表面呈麻面,表面凹凸不平,形成了多条可见的宏观裂纹,试件局部边角破损,且大量粗骨料剥落。
剪切强度与冻融循环次数的关系采用线性表达式描述:
| $ {\varphi _N}(N) = {k_1} + {k_2}N $ | (8) |
式中:φN(N)为剪切强度函数;N为冻融循环次数;k1,k2为回归系数。
利用式(8),对试验数据进行回归分析,得到剪切强度与冻融循环次数的关系式见式(9)。式(9)可决系数R2=0.892 7。对比回归曲线与试验结果(见图 4)可见,两者吻合程度较好。
| $ {\varphi _N}(N) = 4.382\;45 - 0.064N $ | (9) |
应用敏感性分析方法对混凝土剪切强度影响因素进行敏感性分析。设系统特性为混凝土剪切强度,用τi表示, 敏感性影响因素为:法向应力P(0~35 MPa)、应变速率
将混凝土剪切强度与法向应力的函数关系式(4)、剪切强度与应变速率的函数关系式(7)和剪切强度与冻融循环次数的函数关系式(9)分别代入式(2)中,整理得到敏感性函数:
| $ {S_p}(P) = \frac{{0.291\;54P}}{{P + 0.176\;67}} $ | (10) |
| $ {S_{\dot \varepsilon }}(\dot \varepsilon ) = \frac{{0.194\;56\dot \varepsilon }}{{0.194\;56\dot \varepsilon + 5.970\;33}} $ | (11) |
| $ {S_N}(N) = \frac{{ - 0.064N}}{{ - 0.064N + 4.382\;45}}\quad (N \le 50) $ | (12) |
由式(10)~(12)得到各影响因素在其变化范围内的敏感性系数波动范围见表 1。敏感性函数曲线Sp(P)-P,S
| 表 1 混凝土剪切强度影响因素的取值范围与敏感性系数范围 Tab.1 Range of factors affecting concrete shear strength and range of sensitivity coefficients |
|
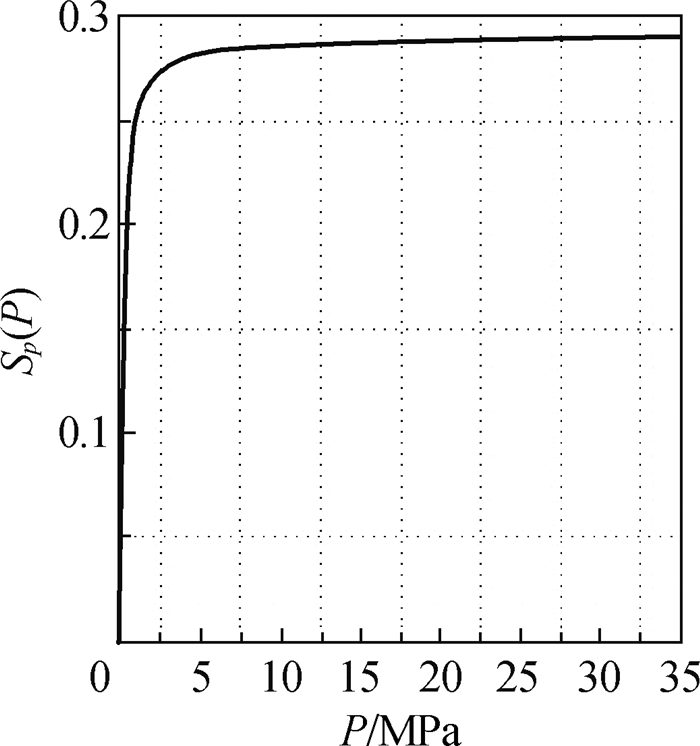
图 6 Sp(P)-P关系曲线 Fig.6 Relationship between sensitivity function and normal stress |

|
图 7 S |
|
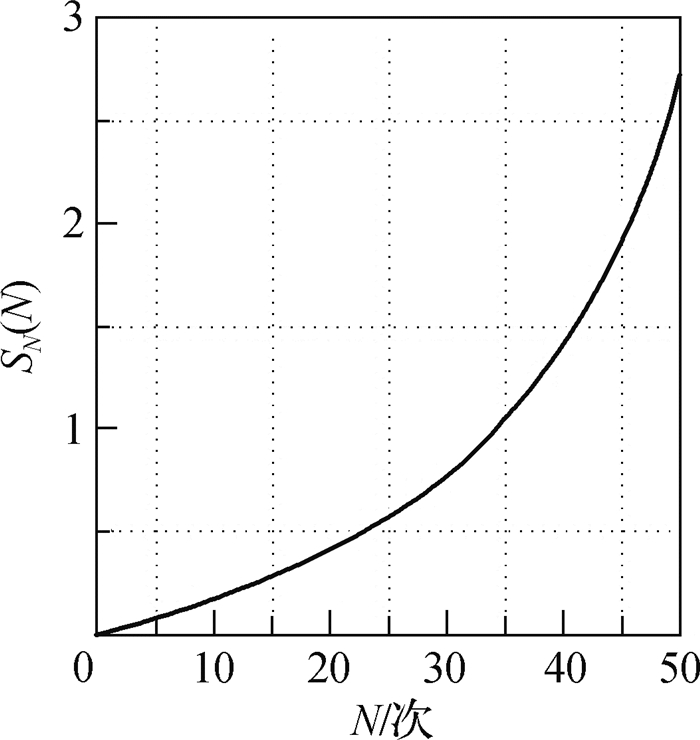
图 8 SN(N)-N关系曲线 Fig.8 Relationship between sensitivity function and freeze-thaw cycles |
(1) 敏感性函数Sp(P)是一个单调递增函数,且存在极限。当法向应力为0~10 MPa时,敏感性系数Sp随法向应力呈线性增加;当法向应力为10~35 MPa时,敏感性系数Sp趋于极限值0.291 54,说明法向应力为0~35 MPa时,敏感性系数Sp约等于0.292。
(2) 敏感性函数S
通过混凝土剪切强度力学性能试验,考察了法向应力、应变速率和冻融循环次数等3种因素对混凝土剪切强度力学参数的影响,利用无量纲形式的敏感性函数对试验因素进行敏感性排序,得到以下结论:
(1) 混凝土的剪切强度随应变速率增大而提高的一个重要因素是,在动态荷载作用下,混凝土内部裂缝和孔隙中存在的自由水移动产生黏性阻力;混凝土的剪切强度随冻融循环次数的增加而降低是因为混凝土历经冻融劣化后混凝土内部孔隙结构改变,孔隙率变大;混凝土的剪切强度随法向应力的增大而提高,其试验曲线可分为线性上升段、非线性上升段和稳定段。
(2) 在敏感性系数波动范围内,冻融循环次数是造成混凝土剪切强度改变最为敏感的因素,该敏感性系数随冻融循环次数的增加而逐渐增加;法向应力对混凝土剪切强度的敏感性仅次于冻融循环次数,不同的是,在法向应力0~10 MPa时,敏感性系数迅速增加,而在10 MPa以后,法向应力对剪切强度的敏感性系数趋于稳定;应变速率对混凝土剪切强度的敏感性最低,在应变速率为10-5/s~10-3/s时,敏感性系数仅有轻微增大。
| [1] |
张琦, 过镇海. 砼抗剪强度和剪切变形的研究[J]. 建筑结构学报, 1992, 13(5): 17-24. ( ZHANG Qi, GUO Zhenhai. Investigation on shear and shear strain of concrete[J]. Journal of Building Structures, 1992, 13(5): 17-24. (in Chinese)) |
| [2] |
李平先, 张雷顺. 冻融循环作用下混凝土的剪切强度试验研究[J]. 郑州大学学报(工学版), 2004, 25(4): 12-15. ( LI Pingxian, ZHANG Leishun. Experimental research on shear strength of concrete subjected to freezing-and-thawing[J]. Journal of Zhengzhou University(Engineering Science), 2004, 25(4): 12-15. DOI:10.3969/j.issn.1671-6833.2004.04.004 (in Chinese)) |
| [3] |
郭艳华, 刘建红, 李志业. 钢纤维混凝土压剪破坏研究[J]. 建筑材料学报, 2008, 11(2): 152-156. ( GUO Yanhua, LIU Jianhong, LI Zhiye. Study on compression-shear failure of steel fiber reinforced concrete[J]. Journal of Building Materials, 2008, 11(2): 152-156. DOI:10.3969/j.issn.1007-9629.2008.02.005 (in Chinese)) |
| [4] |
王怀亮, 宋玉普. 多轴应力条件下碾压混凝土层面抗剪强度试验研究[J]. 水利学报, 2011, 42(9): 1095-1109. ( WANG Huailiang, SONG Yupu. Mechanical properties of roller compacted concrete under multiaxial stress state[J]. Journal of Hydraulic Engineering, 2011, 42(9): 1095-1109. (in Chinese)) |
| [5] |
王刚, 刘黎萍, 孙立军. 沥青混凝土抗剪强度及抗压回弹模量试验研究[J]. 建筑材料学报, 2012, 15(2): 279-282. ( WANG Gang, LIU Liping, SUN Lijun. Research on shearing strength and compressive resilient modulus experiment of asphalt concrete[J]. Journal of Building Materials, 2012, 15(2): 279-282. DOI:10.3969/j.issn.1007-9629.2012.02.026 (in Chinese)) |
| [6] |
宋玉普, 闻伟, 王怀亮. 碾压混凝土压剪强度分析[J]. 水利与建筑工程学报, 2012, 10(6): 44-47. ( SONG Yupu, WEN Wei, WANG Huailiang. Analysis on compression-shear strength of roller compacted concrete[J]. Journal of Water Resources and Architectural Engineering, 2012, 10(6): 44-47. DOI:10.3969/j.issn.1672-1144.2012.06.011 (in Chinese)) |
| [7] |
丛宇, 孔亮, 郑颖人, 等. 混凝土材料剪切强度的试验研究[J]. 混凝土, 2015(5): 40-45. ( CONG Yu, KONG Liang, ZHENG Yingren, et al. Experimental study on shear strength of concrete[J]. Concrete, 2015(5): 40-45. DOI:10.3969/j.issn.1002-3550.2015.05.011 (in Chinese)) |
| [8] |
郭辉, 鹿群, 张丽娟, 等. 钢纤维再生混凝土剪切性能的正交实验研究[J]. 世界地震工程, 2016, 32(2): 107-112. ( GUO Hui, LU Qun, ZHANG Lijuan, et al. Shear behavior of steel fiber recycled concrete by orthogonal analysis[J]. World Earthquake Engineering, 2016, 32(2): 107-112. (in Chinese)) |
| [9] |
章光, 朱维申. 参数敏感性分析与试验方案优化[J]. 岩土力学, 1993, 14(1): 51-58. ( ZHANG Guang, ZHU Weishen. Parameter sensitivity analysis and optimizing for test programs[J]. Rock and Soil Mechanics, 1993, 14(1): 51-58. (in Chinese)) |
| [10] |
WANG Hao, WANG Licheng, SONG Yupu, et al. Influence of free water on dynamic behavior of dam concrete under biaxial compression[J]. Construction and Building Materials, 2016(112): 222-231. |
| [11] |
LIMA L J, VIOLINI D, ZERBINO R. Fracture toughness and fracture energy of concrete[M]. Amsterdam: Elsevier Science, 1986: 219-222.
|
| [12] |
WANG H L, LI Q B. Prediction of elastic modulus and Poisson's ratio for unsaturated concrete[J]. International Journal of Solids and Structures, 2007, 44(5): 1370-1379. DOI:10.1016/j.ijsolstr.2006.06.028 |
| [13] |
田威, 张鹏坤, 谢永利, 等. 冻融环境下基于CT技术混凝土孔隙结构的三维分布特征[J]. 长安大学学报(自然科学版), 2016, 36(3): 49-55. ( TIAN Wei, ZHANG Pengkun, XIE Yongli, et al. 3D distribution characteristics on concrete porous structure under freeze-thaw environment based on CT technique[J]. Journal of Chang'an University(Natural Science Edition), 2016, 36(3): 49-55. DOI:10.3969/j.issn.1671-8879.2016.03.008 (in Chinese)) |
| [14] |
宾峰.冻融循环作用下岩石动态力学特性及微观机理研究[D].长沙: 中南大学, 2014. (BIN Feng. Study on dynamic mechanical properties and microstructure mechanism of rock under freeze-thaw cycles[D]. Changsha: Central South University, 2014. (in Chinese)) http://cdmd.cnki.com.cn/Article/CDMD-10533-1014398695.htm
|
| [15] |
许玉娟, 周科平, 李杰林, 等. 冻融岩石核磁共振检测及冻融损伤机制分析[J]. 岩土力学, 2012, 33(10): 3001-3005. ( XU Yujuan, ZHOU Keping, LI Jielin, et al. Study of rock NMR experiment and damage mechanism analysis under freeze-thaw condition[J]. Rock and Soil Mechanics, 2012, 33(10): 3001-3005. (in Chinese)) |
| [16] |
RYSHKEWITCH E. Compression strength of porous sintered alumina and zirconia[J]. Journal of the American Ceramic Society, 2010, 36(2): 65-68. |
 2019
2019 
