2. 水利部水科学与水工程重点实验室,江苏 南京 210029;
3. 河海大学,港口海岸与近海工程学院,江苏 南京 210098
混凝土抗压强度试验中,标准立方体试件并不处于均匀受压应力状态,所测强度值也绝非理想的单轴抗压强度[1]。混凝土多轴抗压强度试验时试件各承压面上的约束作用相互影响,可使混凝土试验强度提高1倍、甚至更多[2]。为了减小钢压板与承压面间摩阻力影响,一般设置减摩垫层,使试验抗压强度值接近于无摩擦约束的抗压强度[3-4]。混凝土双轴受压弹模和徐变试件一般为边长100~200 mm的立方体试件,加载应力控制在相应龄期棱柱体强度fpr的30%~40%。混凝土试件表面轻微不平整和倾斜以及钢承压板与试件承压面的摩阻对混凝土双轴弹模和徐变试验结果的影响更大,因此需要在借鉴双轴抗压强度试验减摩垫层的基础上,研究出适用于混凝土双轴弹模和徐变试验、使混凝土试件在弹性变形阶段整体应力应变均匀性好的垫层[5]。
选择不同聚四氟乙烯膜(PTFE)厚度、层数以及与其他材料的组合垫层,通过棱柱体混凝土试件单轴受压弹模试验比较分析其效果,筛选出3种效果相对较好的组合垫层进行双轴弹模验证试验,最终提出能有效减小混凝土试件表面轻微不平整和倾斜以及钢承压板与试件端面摩阻等因素对双轴弹模和徐变试验结果影响的垫层。
1 试验概况 1.1 试验设备试验采用YXB-1000混凝土双轴徐变仪,该设备由加压与恒荷、力值和变形测量、控制与分析三部分组成,可进行混凝土和岩石的双轴弹模与徐变试验。主要性能参数为:最大试验力1 000 kN(竖向、活塞式油缸加载)和500 kN(水平向、伺服电机机械加载),最小分辨力值0.005 kN(竖向)和0.002 5 kN(水平向);变形最大量程10 mm,变形分辨力0.001 mm。加载方式为单独加载或两轴同时加载,加载速率2~200 kN/min,控制方式为力或位移,连续工作不少于1年。加载过程中混凝土试件各部位竖向和横向应变由电阻应变片和电子动态应变仪测量。
1.2 试件制作及应变片布置试验选用C30, C50和C60混凝土分别制作棱柱体试件(150 mm×150 mm×300 mm)和立方体试件(200 mm×200 mm×200 mm)。混凝土骨料最大粒径不大于25 mm。为减小试件表面不平整和倾斜,用特制铁模具卧式成型。
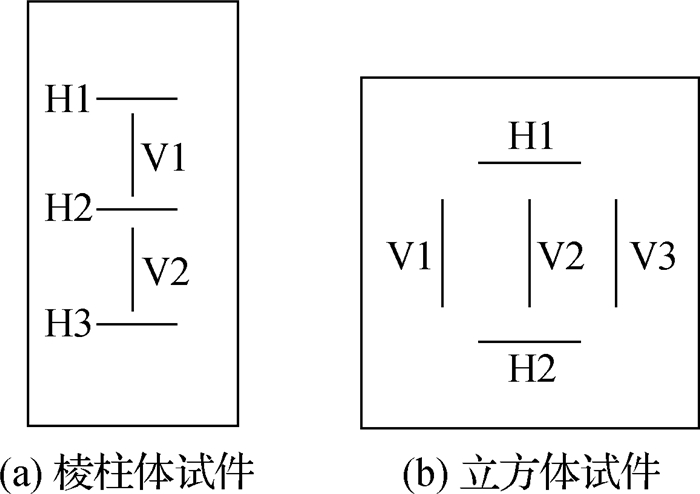
根据圣维南原理,试件加压端面的不均布垂直压应力和合力为零的水平约束力只对端面附近应力状态产生影响。标准棱柱体试件中间部分接近于均匀的单轴受压应力状态。因此用标准棱柱体试件端面附近的横向应变与中部应变相比较以判别垫层效果。试验中棱柱体和立方体应变片布置见图 1。由于混凝土骨料最大粒径不大于25 mm,选用标距80 mm应变片。
|
图 1 应变片布置 Fig.1 Strain gages layout |
选用C30, C50和C60混凝土进行试验,由于垫层效果试验结果与混凝土强度等级基本无关,仅列出C50混凝土试件的试验结果。
单轴加载试验参照混凝土受压弹模和徐变试验方法[6-7],仅在混凝土弹性阶段(0.3~0.4)fpr分级加载,棱柱体试件每级荷载增量50 kN,立方体试件每级荷载增量100 kN,加载速率2 kN/s。正式加载前,将垫层置于加载板与试件承压面之间,预压5 kN荷载后检查加载板、垫层与试件对中情况,如偏差较大则卸荷重新调整。每种垫层进行3次试验,选择相同试件在不同垫层时压板附近与棱柱体中部横向应变的偏差率和两侧竖向偏差率进行比较;每种垫层对3个不同试件进行适用性试验,筛选3种效果相对较好的垫层进行双轴弹模试验验证,最终提出具有适应试件表面轻微不平整和倾斜、减小压板与混凝土试件间摩擦、用于混凝土双轴弹模和徐变试验的垫层。
2 垫层效果试验与分析 2.1 垫层效果评判指标与标准垫层降偏和减摩效果的判别参数包括试件在加载应力小于(0.3~0.4)fpr时不同位置的应变偏差率e、应变曲线以及试验结果计算所得弹性模量E和泊松比μ。
(1) 偏差率 混凝土试件竖向和横向应变均匀性采用偏差率e表示,e按下式计算:
| $ {e_{d, mn}} = \left| {\frac{{{\varepsilon _m} - {\varepsilon _n}}}{{{\varepsilon _m} + {\varepsilon _n}}}} \right| \times 100\% $ | (1) |
式中:ed, mn为试件某方向某位置应变片的应变偏差率,d为应变方向,竖向为V,横向为H;εm,εn为竖向或横向不同位置应变值;m,n表示对应的竖向或横向应变片编号(见图 1);试件前后两侧竖向应变偏差率为eVf, Vb;对于棱柱体试件采用试件两侧中心应变片V1和V2应变值总和计算,立方体试件采用试件两侧中心应变片V2应变值计算;ed表示试件应变偏差率平均值。
试件竖向两侧应变偏差率和横向不同位置应变偏差率越低说明垫层适应混凝土试件表面轻微不平整和倾斜的能力越强,钢压板与试件间减摩效果越好,试件应力分布越均匀。
(2) 加载级的弹模和泊松比
① 双向先后加载 竖向荷载PV先逐级施加至最大值,水平荷载PH=0,由第一级荷载到最大一级荷载的应力增量为σV,应变增量为εV和εH,无侧压力(σH=0)的弹性模量EV、泊松比μV计算式为:
| $ {E_{\rm{v}}} = {\sigma _{\rm{V}}}/{\varepsilon _{\rm{v}}}, {\mu _{\rm{v}}} = - {\varepsilon _{\rm{H}}}/{\varepsilon _{\rm{V}}} $ | (2) |
之后水平荷载PH逐级施加至最大值,竖向荷载PV保持不变,水平向和竖向应变增量分别为ΔεH和ΔεV,有侧压力σV下的弹性模量EH和泊松比μH计算式为:
| $ {E_{\rm{H}}} = {\sigma _{\rm{H}}}/\Delta {\varepsilon _{\rm{H}}}, \quad {\mu _{\rm{H}}} = - \Delta {\varepsilon _{\rm{V}}}/\Delta {\varepsilon _{\rm{H}}} $ | (3) |
② 双向交替加载 试验荷载分8级施加,单级1,3,5,7级加竖向荷载ΔPV,双级2,4,6,8级加水平荷载ΔPH;加竖向荷载时保持上一级水平荷载不变,加水平荷载时保持上一级竖向荷载不变。弹性特征计算式为:
| $ {E_{\rm{v}}} = \frac{{4\Delta {\sigma _{\rm{V}}}}}{{\Delta {\varepsilon _{{{\rm{V}}_2}}} + \Delta {\varepsilon _{{{\rm{V}}_3}}} + \Delta {\varepsilon _{{{\rm{V}}_5}}} + \Delta {\varepsilon _{{{\rm{V}}_7}}}}}, \;\;\;{\mu _{\rm{V}}} = - \frac{{\Delta {\varepsilon _{{{\rm{H}}_1}}} + \Delta {\varepsilon _{{\rm{H}}3}} + \Delta {\varepsilon _{{{\rm{H}}_5}}} + \Delta {\varepsilon _{{{\rm{H}}_7}}}}}{{\Delta {\varepsilon _{{{\rm{V}}_1}}} + \Delta {\varepsilon _{{{\rm{V}}_3}}} + \Delta {\varepsilon _{{{\rm{V}}_5}}} + \Delta {\varepsilon _{{{\rm{V}}_7}}}}} $ | (4) |
| $ {E_{\rm{H}}} = \frac{{4\Delta {\sigma _{\rm{H}}}}}{{\Delta {\varepsilon _{{{\rm{H}}_2}}} + \Delta {\varepsilon _{{{\rm{H}}_4}}} + \Delta {\varepsilon _{{{\rm{H}}_6}}} + \Delta {\varepsilon _{{{\rm{H}}_{\rm{8}}}}}}}, \;\;\;{\mu _{\rm{H}}} = - \frac{{\Delta {\varepsilon _{{{\rm{V}}_2}}} + \Delta {\varepsilon _{{{\rm{V}}_4}}} + \Delta {\varepsilon _{{{\rm{V}}_6}}} + \Delta {\varepsilon _{{{\rm{V}}_8}}}}}{{\Delta {\varepsilon _{{{\rm{H}}_2}}} + \Delta {\varepsilon _{{{\rm{H}}_4}}} + \Delta {\varepsilon _{{{\rm{H}}_6}}} + \Delta {\varepsilon _{{{\rm{H}}_{\rm{8}}}}}}} $ | (5) |
弹性阶段各加载级应变增量越均匀则垫层效果越好,表现为各加载级弹模E和泊松比μ的标准差大小,标准差越小垫层效果越好。
(3) 适用性 混凝土试件制作过程中表面不可避免存在轻微的不平整和倾斜,表面的粗糙程度也不相同,而且这些缺陷是随机的。混凝土立方体抗压强度试验时规范规定试件承压面不平整度不应大于试件边长的0.05%,承压面与相邻面的不垂直度不应大于±1°。相同垫层不同试件的试验结果越接近,说明垫层的适用性越好。
2.2 垫层材料选择针对混凝土受压弹模-徐变试验加载应力较小、承压面不平整和倾斜以及试件表面粗糙度对试验结果影响大的特点,应选择既能适应承压面不平整和倾斜,又具有减摩功能的垫层。根据相关研究成果[8],选用聚四氟乙烯薄膜(PTFE)、氯丁橡胶薄板、瓦楞纸板和土工布等作为垫层主要材料或辅助材料进行试验。
国内外采用最多的减摩垫层材料是PTFE[9-12],它是典型的软而弱聚合物,大分子间的相互引力较小,刚度、硬度、强度都较小,在应力长期作用下会出现蠕变,摩阻系数小(约为0.01~0.10);氯丁橡胶也是常用垫层材料,具有良好拉伸强度、伸长率,且变形可逆;瓦楞纸板是一个多层的黏合体,弹性小,易变形,缓冲作用好,可根据需要制成各种形状,或大或小,但重复性较差,且不宜在湿度较大的环境中长期使用;土工布(无纺)又称土工织物,抗拉强度高,与其他材料组合使用,可起到加筋作用,减少其他软体的延伸变形,对试件表面的不平整和倾斜适应性高。
2.3 单一材料垫层效果以PTFE为垫层材料,分析不同厚度PTFE垫层对棱柱体单轴受压试件应变偏差率、应变曲线及弹性特征计算结果的影响。
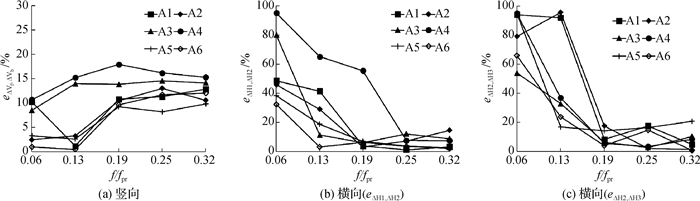
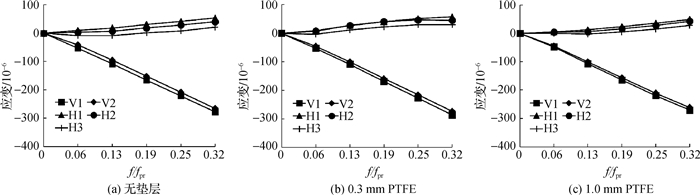
表 1和2为不同厚度PTFE垫层混凝土试件总应变偏差率和试件不同荷载级应变增量计算的弹模E与泊松比μ结果;图 2为不同厚度垫层混凝土试件应变偏差率e随荷载的变化曲线;图 3为无垫层、0.3 mmPTFE和1.0 mm PTFE垫层混凝土试件应变随荷载增长曲线。
| 表 1 不同厚度PTFE垫层混凝土试件竖向和横向总应变偏差率 Tab.1 Vertical and lateral total strain deviation rates of concrete specimens with different-thickness PTFE cushions |
| 表 2 不同厚度PTFE垫层各荷载级弹模及泊松比试验结果 Tab.2 Elastic modulus and Poisson's ratio test results for different-thickness PTFE cushions under all load levels |
|
图 2 不同厚度PTFE垫层混凝土试件各荷载级应变增量偏差率 Fig.2 Strain deviation rate of concrete specimens with different-thickness PTFE cushions under all load levels |
|
图 3 不同厚度PTFE垫层的混凝土试件应变曲线 Fig.3 Strain curves of concrete specimens with different-thickness PTFE cushions |
试验结果表明:
(1) 混凝土试件横向应变偏差率总体上随PTFE垫层厚度增加而降低,无垫层试件平均横向应变偏差率为22.83%,使用1.0 mm PTFE垫层后试件平均横向应变偏差率下降至13.73%。
(2) 横向应变偏差率随混凝土试件应力水平提高先期下降明显,应力大于0.25fpr后,混凝土试件横向应变偏差率逐渐趋于稳定。
(3) PTFE垫层厚度对混凝土试件竖向应变偏差率的影响不明显,不同垫层时试件竖向应变偏差率eVf, Vb为4.86%~15.23%,其中0.3 mm PTFE垫层最高,1.0 mm PTFE垫层最低,无垫层为9.31%。
(4) 不同厚度PTFE垫层混凝土试件各荷载级计算的弹模为39.9~42.1 GPa,标准差2.90~3.90 GPa;泊松比0.14~0.17,标准差0.062~0.112。
(5) 虽然试件承压面设置单层PTFE垫层可一定程度降低试件竖向和横向应变偏差率,应力分布随荷载增长的曲线也逐渐趋于均匀,但其横向最大应变偏差率仍较高,弹性特征标准差也较大,难以满足弹模和徐变试验要求。
(6) 对于混凝土双轴弹模和徐变试验,受试件表面轻微不平整和倾斜影响,试件应力较小时应变偏差率较大,因此理想垫层应以调整试件表面轻微不平整和倾斜的功能为主,压板与试件间减摩为辅。
2.4 组合垫层效果根据混凝土双轴弹模和徐变试验对垫层功能的要求,在不同厚度PTFE垫层试验基础上,进一步比较PTFE与其他材料的组合垫层对棱柱体和立方体试件应变偏差率、应变曲线及弹性特征的影响。
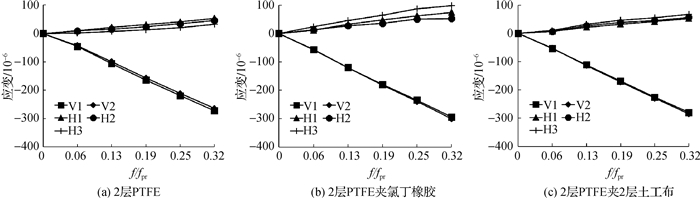
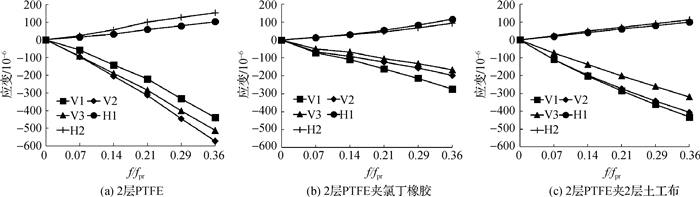
不同组合垫层混凝土试件应变偏差率见表 3,棱柱体和立方体试件应变随荷载增长曲线见图 4和5,不同组合垫层棱柱体和立方体试件弹模、泊松比与标准差试验结果见图 6。
| 表 3 组合垫层混凝土试件横竖向总应变偏差率 Tab.3 Horizontal and vertical total strain deviation rates of concrete specimens with different composite cushions |
|
图 4 不同垫层组合棱柱体试件应变曲线 Fig.4 Strain curves of prism specimens with different cushions |
|
图 5 不同垫层组合立方体试件应变曲线 Fig.5 Strain curves of cubic specimens with different cushions |

|
图 6 不同垫层组合各荷载级弹模和泊松比及其标准差 Fig.6 Standard deviation of elastic modulus and Poisson's ratio with different cushions under all load levels |
通过试验结果分析发现:
(1) 不同组合垫层棱柱体试件竖向应变偏差率eVf, Vb为3.83%~16.46%,其中2层1.0 mm PTFE夹瓦楞纸板垫层最高,2层1.0 mm PTFE夹0.6 mm土工布垫层最低。
(2) 棱柱体试件在不同组合垫层时横向应变偏差率eH为3.89%~34.33%,2层1.0 mm PTFE夹土工布垫层最大横向应变偏差率eH, max相对较小(8.55%~16.97%),其中2层1.0 mm PTFE夹1.2 mm和0.6 mm土工布的垫层最低。
(3) 不同组合垫层立方体试件横向应变偏差率eH1, H2为4.30%~19.66%,其中2层1.0 mm PTFE垫层最高,2层1.0 mm PTFE夹0.6 mm土工布垫层最低。
(4) 立方体试件在不同组合垫层时竖向应变偏差率eV为0.26%~31.63%,2层1.0 mm PTFE垫层和2层1.0 mm PTFE夹土工布垫层最大竖向应变偏差率相对较小(10.25%~14.87%),其中2层1.0 mm PTFE夹1.2 mm土工布最低。
(5) 不同组合垫层棱柱体试件各荷载级的计算弹模为37.5~41.8 GPa,标准差1.78~4.90 GPa,其中2层PTFE夹土工布垫层的弹模标准差相对较小;泊松比为0.14~0.25,标准差为0.038~0.166,2层1.0 mm PTFE垫层和2层1.0 mm PTFE夹土工布垫层的泊松比标准差相对较小。
(6) 不同组合垫层立方体试件各荷载级的计算弹模为29.6~67.7 GPa,标准差1.10~18.87 GPa,其中2层1.0 mm PTFE夹瓦楞纸板垫层弹模标准差相对较小;泊松比为0.25~0.54,标准差为0.015~0.175,其中2层1.0 mm PTFE夹瓦楞纸板垫层、2层1.0 mm PTFE夹1.2 mm土工布、2层1.0 mm PTFE夹1.2 mm和0.6 mm垫层的泊松比标准差相对较小。
(7) 各组合垫层棱柱体和立方体试件随着荷载增加,其竖向和横向应变偏差率逐渐减小,应力分布趋于均匀,试验结果推算的弹模、泊松比趋于稳定。
(8) 综合比较棱柱体和立方体试件竖向和横向应变偏差率、计算弹模和泊松比及标准差等参数, 结果表明,2层1.0 mm PTFE夹土工布的组合垫层效果明显优于PTFE夹氯丁橡胶和PTFE夹瓦楞纸板的组合垫层。
3 组合垫层在双轴弹模试验中的应用对棱柱体和立方体单轴试验筛选效果相对较好的2层1.0 mm厚PTFE夹土工布(土工布厚度0.6, 1.2, (0.6+1.2) mm)组合垫层进行双轴受压弹模试验验证。
试验时采用3种不同加载顺序分别对3个立方体试件进行双轴受压试验。试验分8级加载,每级荷载增量100 kN,最大应力控制在(0.3~0.4)fpr,每个试件每种垫层试验3次。同时把同一试件不同组合垫层竖向两侧偏差率eVf, Vb试验结果与同一组合垫层在3个不同试件的试验结果进行综合比较。
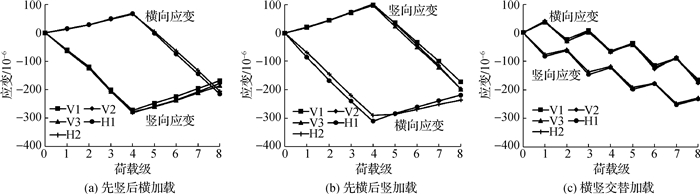
不同加载顺序双轴受压试验各试件应变偏差率及弹模和泊松比计算结果见表 4,PTFE夹1.2 mm土工布垫层试件应变随荷载的变化曲线见图 7。
| 表 4 PTFE夹土工布组合垫层双轴受压试验结果 Tab.4 Biaxial compression test results of composite cushion with PTFE and geotextile |
|
图 7 PTFE夹1.2 mm土工布组合垫层应变曲线 Fig.7 Strain curves of composite cushion with PTFE and 1.2 mm geotextile |
(1) 不同加载顺序立方体试件3种组合垫层最大应变偏差率emax为0.49%~10.13%,其中2层1.0 mm PTFE夹1.2 mm土工布垫层3个加载顺序试件的最大应变偏差率emax均最低,分别为0.49%, 2.80%和9.86%。
(2) 不同加载顺序立方体试件3种组合垫层竖向弹模EV为32.1~38.5 GPa,横向弹模EH为31.3~36.3 GPa,EV和EH偏差率为0~10.32%。其中2层1.0 mm PTFE夹1.2 mm土工布垫层3个加载顺序试件EV和EH的偏差均最低,分别为0,2.06%和0.93%。
(3) 不同加载顺序立方体试件3种组合垫层竖向泊松比μV为0.22~0.28,横向泊松比μH为0.32~0.45,μV和μH偏差率为6.67%~32.31%。其中2层1.0 mm PTFE夹0.6 mm土工布垫层3个加载顺序试件μV和μH偏差均最低,分别为16.92%,11.11%和6.67%。
(4) 3个加载顺序立方体试件2层1.0 mm PTFE夹1.2 mm土工布垫层试件横竖向应变在整个加载过程中较为均匀。
(5) PTFE夹土工布的3种组合垫层均能在双轴受压弹模试验中有效降低试件竖向和横向应变偏差率,使混凝土试件应力分布均匀。经综合比较分析可见,2层1.0 mm PTFE夹1.2 mm土工布的组合垫层效果又优于夹0.6 mm和(0.6+1.2)mm土工布的组合垫层。
4 结语通过混凝土棱柱体和立方体试件单轴受压时单一垫层与组合垫层对应变偏差率、应变曲线及弹性特征影响的比较,筛选3种垫层进行双轴弹模试验验证,得出以下结论:
(1) 混凝土试件在应力水平较低时(小于0.25fpr),试件表面轻微不平整和倾斜对应力分布影响最为敏感,应变偏差率较大,因此混凝土双轴弹模和徐变试验的垫层应以调整试件表面轻微不平整和倾斜的功能为主,压板与试件间的减摩为辅。
(2) 试件承压面上设置单层PTFE垫层可一定程度降低试件竖向和横向应变偏差率,应力分布随荷载增长的曲线也更均匀,但其横向最大应变偏差率仍较高,且弹性特征标准差也较大,难以满足双轴弹模和徐变试验要求。
(3) 综合比较试件竖向和横向应变偏差率、计算弹模和泊松比及标准差等参数发现,2层1.0 mm PTFE夹土工布的组合垫层效果明显优于PTFE夹氯丁橡胶和PTFE夹瓦楞纸板的组合垫层。
(4) PTFE夹土工布的组合垫层能有效降低试件竖向和横向应变偏差率,使试件应力分布均匀。2层1.0 mm PTFE夹1.2 mm土工布的组合垫层效果总体优于2层1.0 mm PTFE夹0.6 mm和(0.6+1.2)mm土工布的组合垫层。
(5) 混凝土单、双轴弹模和徐变试验中推荐使用2层1.0 mm厚PTFE夹1.2 mm土工布的组合垫层,该组合垫层装置已取得国家知识产权局的实用新型专利授权[13]。
| [1] |
过镇海. 混凝土的强度和变形:试验基础和本构关系[M]. 北京: 清华大学出版社, 1997. ( GUO Zhenhai. Strength and deformation of concrete: experimental basis and constitutive relationship[M]. Beijing: Tsinghua University Press, 1997. (in Chinese))
|
| [2] |
王传志, 过镇海, 张秀琴. 二轴和三轴受压混凝土的强度试验[J]. 土木工程学报, 1987(1): 15-27. ( WANG Chuanzhi, GUO Zhenhai, ZHANG Xiuqin. Experimental investigation of concrete strength under biaxial and triaxial compressive stresses[J]. China Civil Engineering Journal, 1987(1): 15-27. (in Chinese)) |
| [3] |
邓宗才, 阚德新, 杜修力, 等. 聚乙烯纤维布约束混凝土短柱轴压性能的试验[J]. 工业建筑, 2007(10): 69-72. ( DENG Zongcai, KAN Dexin, DU Xiuli, et al. Experiment on behavior of concrete short columns confined by polyethylene fiber sheet under axial compression[J]. Industrial Construction, 2007(10): 69-72. (in Chinese)) |
| [4] |
曾莎洁, 李杰. 混凝土单轴受压动力全曲线试验研究[J]. 同济大学学报(自然科学版), 2013(1): 7-10. ( ZENG Shajie, LI Jie. Experiment study on uniaxial compression behavior of concrete under dynamic loading[J]. Journal of Tongji University (Natural Science), 2013(1): 7-10. DOI:10.3969/j.issn.0253-374x.2013.01.002 (in Chinese)) |
| [5] |
陈灿明.双向受力状态下混凝土受力特性与混凝土双轴徐变仪的开发应用研究[R].南京: 南京水利科学研究院, 2015. (CHEN Canming. Study on concrete stress characteristics under two-way stress state and development of concrete biaxial creeper[R]. Nanjing: Nanjing Hydraulic Research Institute, 2015. (in Chinese))
|
| [6] |
GB-T 50082—2009普通混凝土长期性能和耐久性能试验方法标准[S]. (GB-T 50082—2009 Standard for test methods of long-term performance and durability of ordinary concrete[S]. (in Chinese))
|
| [7] |
SL 352—2006水工混凝土试验规程[S]. (SL 352—2006 Test code for hydraulic concrete[S]. (in Chinese))
|
| [8] |
张秀琴, 王传志.混凝土立方体试块表面摩擦对强度的影响及其减摩措施[R].北京: 清华大学抗震抗爆工程研究室, 1983. (ZHANG Xiuqin, WANG Chuanzhi. Effect of surface friction on strength of cubed concrete and its anti-friction measures[R]. Beijing: Tsinghua University Earthquake Resistant Engineering Laboratory, 1983. (in Chinese))
|
| [9] |
LU X B, THOMAS C T T. Behavior of high strength concrete with and without steel fiber reinforcement in triaxial compression[J]. Cement and Concrete Research, 2006, 36(9): 1679-1685. DOI:10.1016/j.cemconres.2006.05.021 |
| [10] |
LEE S K, SONG Y C, HAN S H. Biaxial behavior of plain concrete of nuclear containment building[J]. Nuclear Engineering and Design, 2004, 227(2): 143-153. DOI:10.1016/j.nucengdes.2003.09.001 |
| [11] |
宋玉普, 何振军. 高强高性能混凝土在多轴压下强度与变形性能的试验研究[J]. 岩石力学与工程学报, 2008, 27(增刊2): 3575-3584. ( SONG Yupu, HE Zhenjun. Experimental investigation on strength and deformation of plain high-strength high-performance concrete under multiaxial compression[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(Suppl2): 3575-3584. (in Chinese)) |
| [12] |
肖平成, 李奔奔, 江佳斐. 减摩擦垫层对混凝土轴压试验的影响[J]. 材料科学与工程学报, 2015(1): 127-132. ( XIAO Pingcheng, LI Benben, JIANG Jiafei. Effect of friction-reducing pads on concrete under compression[J]. Journal of Materials Science and Engineering, 2015(1): 127-132. (in Chinese)) |
| [13] |
陈灿明.混凝土双轴压缩试验的垫层组合装置: 中国, ZL201620733232.2[P]. 2016-12-07. (CHEN Canming. Cushion combination device for concrete biaxial compression test: China, ZL201620733232.2[P]. 2016-12-07. (in Chinese))
|
2. Key Laboratory of Water Science and Water Engineering of Ministry of Water Resources, Nanjing 210029, China;
3. College of Harbour, Coastal and Offshore Engineering, Hohai University, Nanjing 210098, China
 2019
2019 
