2. 山东交通职业学院 公路与建筑系,山东 潍坊 261206;
3. 中国海洋大学 工程学院,山东 青岛 266100
在河流、海洋工程中,地基上部土层中多见细砂层,其与下部基础的界面摩阻力是下部结构承载力的重要组成部分,研究结构物-砂土界面剪切特性具有重要的工程价值。室内直剪试验是研究结构物-土界面剪切特性的重要途径,国内外学者对此进行了广泛的试验研究。夏红春等[1]利用超高压直残剪试验系统研究了粗糙钢板-标准砂界面剪切特性,指出在高法向应力下剪应力-位移关系呈现应变软化、线性强化和应变强化3种类型。Mortara等[2]进行了常刚度条件下的钢-硅质砂界面剪切试验,强调剪切应力的退化对终值剪切应力的重要影响。田建勃等[3]研究了砂粒径对界面力学特性的影响,认为界面厚度随砂粒径的增大而增加。陆勇等[4]研究了结构面峰谷距与砂平均粒径相对尺度对界面剪切特性的影响,认为存在“极限相对尺度”和“临界相对尺度”。徐超等[5]进行了标准砂-土工格栅界面循环剪切试验,认为加筋可有效限制界面法向位移。王军等[6]进行了标准砂-玻璃纤维大型直剪试验,指出格栅纵横肋的合理搭配比例能够显著提高界面剪切强度。梁越等[7]利用改进的直剪仪研究了不同预压时间下的钢-土界面剪切特性,发现极限剪应力与预压时间成正比关系,在法向应力较小时极限剪应力的时效性较明显。Liu等[8]进行了砂-土工合成材料循环后单剪试验,指出峰值和残余剪应力与正应力、循环次数呈正相关关系,界面表观黏聚力和摩擦角随剪切强度增加而增大。赵联桢等[9]研究了冻砂土与结构接触面在恒温条件下的剪切特性。肖杰等[10]利用大型界面直剪仪研究了硫酸腐蚀对砂-混凝土界面剪切性状的影响,用双曲线模型对剪应力-位移关系进行了较好的拟合。Farhadi等[11]研究了砂的初始各向异性对钢-砂界面剪切行为的影响,指出峰值剪应力和最大剪胀角受层面倾角影响较大。Gu等[12]通过室内试验和离散元模拟比较,从宏观和微观角度研究了界面应变局部化和剪胀行为,提供了一种基于剪切带临界状态的定量建模方法。金子豪等[13]研究了粗糙度对混凝土-砂界面力学特性的影响,指出平均粒径大于0.7 mm的粗砂和细砾,剪切带厚度约为5D50。
本文利用改进的室内直剪仪,选取粒径为0.075~0.150 mm和0.150~0.300 mm的两组砂,进行砂与人造粗糙钢板和混凝土板的界面剪切试验,重点探讨法向应力变化、粒组变化、粗糙度变化、结构物材料变化对界面剪切特性的影响。
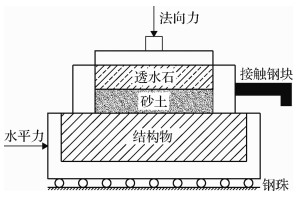
1 界面剪切试验 1.1 试验设备界面剪切试验所用直剪仪是在室内应变控制式直剪仪基础上经过改进制作而成,如图 1所示。上剪切盒放置砂土和透水石,砂土体积为30 cm2×1.25 cm,下剪切盒经机械加工而成,盒内放入钢板或混凝土板,因钢板、混凝土板与下剪切盒结合密实,为避免产生气压,同时方便取样,在下盒底面正中央打一贯通圆孔,改进后的直剪仪下盒如图 2所示。由于砂土边缘距离结构物边缘为17 mm,可保证试验过程中砂土与钢板的接触面积保持不变。
|
图 1 改进后的直剪仪示意图 Fig.1 Sketch of improved direct shear apparatus |

|
图 2 改进后的直剪仪下盒 Fig.2 Lower box for improved direct shear apparatus |
试验所用砂土取自潍坊,界面剪切试验选用经筛分、烘箱烘干后的两种粒径组的砂,分别为粒组Ⅰ(0.075~0.150 mm)、粒组Ⅱ(0.150~0.300 mm)。试验所用砂土的主要物理力学指标见表 1。
| 表 1 试验土样主要物理力学性质指标 Tab.1 Main physical and mechanical properties of soil |
试验所用钢板为不锈钢材料,产自潍坊本地钢材公司,钢板经机械加工制作而成,尺寸为10.1 cm×9.6 cm×2.5 cm,4个角位置处设φ 6 mm的倒圆角。钢板共4块,可模拟4种不同表面粗糙度的结构物,其中粗糙度Ⅰ的钢板表面不做任何处理,粗糙度Ⅱ、粗糙度Ⅲ和粗糙度Ⅳ的钢板采用机械设备在其表面分别刻5道、7道和9道纹路,纹路为倒三角形,纹路长度方向与界面剪切方向相垂直,试验所用钢板如图 3所示。试验所用混凝土尺寸同钢板,为保证混凝土块能够较好地与下剪切盒契合,经机械加工一钢试模,内模空间尺寸与钢板尺寸一致,如图 4所示。混凝土板经预制而成,配比为石:砂:水:水泥=905:905:240:475,其中石子的粒径范围为4.75~9.50 mm。养护完成后的混凝土板共4块,随即制作同钢板粗糙度Ⅱ,Ⅲ,Ⅳ一致的混凝土板,粗糙度Ⅰ的混凝土板不做处理,如图 5所示。钢板、混凝土板制作完成后,其表面粗糙度采用灌砂法[14]测量,用平均灌砂深度h表示处理面的粗糙度,h越大则粗糙度越大。具体方法为:用4片塑料板将试块处理面围起来,使塑料板的最高平面和处理面的最高点平齐,在表面灌入粉细砂(0.075~0.150 mm)且与塑料板顶面抹平,然后测得灌入砂的体积,重复测量3次,则平均灌砂深度(h)=砂的体积V/处理面表面积S。假定粗糙度Ⅰ,Ⅱ,Ⅲ和Ⅳ的平均灌砂深度为h1,h2,h3和h4,计算结果如表 2所示。

|
图 3 试验所用钢板 Fig.3 Steel plate used in the test |

|
图 4 试验所用混凝土试模 Fig.4 Template of concrete used in the test |

|
图 5 试验所用混凝土板 Fig.5 Concrete plate used in the test |
| 表 2 试块表面粗糙度 Tab.2 Surface roughness of test block samples |
下剪切盒分别放入粗糙度Ⅰ~Ⅳ的钢板和粗糙度Ⅰ~Ⅳ的混凝土板,上剪切盒分别填入粒组Ⅰ(0.075~0.150 mm)和粒组Ⅱ(0.150~0.300 mm)的砂土,为保证砂样初始状态的一致性,对于同一粒组的砂,向上剪切盒加入相同质量的砂,且每组试验均在法向应力50 kPa下预压5 min,然后在法向应力50,100,150和200 kPa作用下进行剪切试验,界面剪切试验共64组。试验采用位移控制加载方式,剪切速率设定在0.8 mm/min。
2 试验机理分析 2.1 界面抗剪强度根据试验得到的粗糙度Ⅰ~Ⅳ的钢板、混凝土板与粒组Ⅰ,Ⅱ的砂界面剪切应力-剪切位移数据可知:剪切应力随着剪切位移增大而增加,在剪切初始阶段,剪切应力的增速最快,随着剪切位移的增加,剪切应力增速变缓,直至达到剪切应力峰值,之后剪切应力基本趋于稳定,但出现小幅度波动,整体略有软化的趋势。因剪切应力-剪切位移曲线的形状接近双曲线,采用Clough和Duncan提出的双曲线模型[15]对试验数据进行研究,模型计算式为:
| $ \tau = \omega /(a + b\omega ) $ | (1) |
式中:a为初始剪切刚度Ks0的倒数;b为极限剪切应力τu的倒数。双曲线模型计算式及相关试验数据见表 3~4,τf为试验峰值剪切应力,τu为模型峰值剪切应力。
| 表 3 钢-砂界面拟合公式及试验数据 Tab.3 Fitting formula and experimental data of interface between steel and sand |
| 表 4 混凝土-砂界面拟合公式及试验数据 Tab.4 Fitting formula and experimental data of interface between concrete and sand |
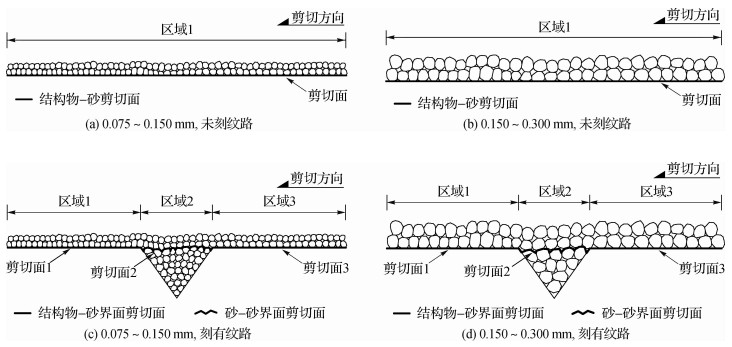
从表 3和4可以看出:①在同一粗糙度和粒组条件下,试验峰值剪切应力随法向应力的增大而增加。②在同一法向应力和粒组条件下,试验峰值剪切应力随粗糙度的增大而增加,峰值剪切应力从粗糙度Ⅰ到粗糙度Ⅱ的增加值最大,而峰值剪切应力从粗糙度Ⅱ到粗糙度Ⅲ及从粗糙度Ⅲ到粗糙度Ⅳ的增加值相对较小,且比较接近,原因是钢和混凝土所刻纹路的数量均为0,5,7,9道,从粗糙度Ⅰ到粗糙度Ⅱ、粗糙度Ⅱ到粗糙度Ⅲ、粗糙度Ⅲ到粗糙度Ⅳ钢板的平均灌砂深度增加值分别为0.056,0.025和0.021 mm,混凝土板的平均灌砂深度增加值分别为0.073,0.020和0.023 mm,平均灌砂深度的增加值越大,说明粗糙度提高得越大,故峰值剪切应力变化越大;峰值剪切位移随粗糙度的增大也基本呈现出相同的规律,且从粗糙度Ⅰ到粗糙度Ⅱ的增加值最大。③在同一粗糙度和法向应力条件下,粒组Ⅰ和粒组Ⅱ的试验峰值剪切应力比较接近,但粒组Ⅱ要小于粒组Ⅰ,这与砂本身的粗糙度及砂与结构物的接触面积有关系,绘制结构物-砂剪切面形成示意图(见图 6(a)和(b))。在粗糙度Ⅰ条件下,由于粒组Ⅰ的粒径要小于粒组Ⅱ的粒径,其与结构物的接触面积更大,导致粒组Ⅰ的峰值剪切应力要比粒组Ⅱ的略大一些;在粗糙度Ⅱ,Ⅲ和Ⅳ条件下,峰值剪切应力由三部分组成。为更好地分析界面剪切强度构成,绘制结构物-砂界面剪切面构成示意图(见图 6(c)和(d))。一部分为未刻纹路区域得到的结构物-砂界面剪切应力(区域1和区域3),一部分为刻纹路区域的砂-砂界面剪切应力(区域2),另一部分为相邻区域交界处棱角提供的剪切应力。由于纹路的宽度和深度相对砂粒径较大,一定数量的砂在剪切过程中就一直嵌锁在纹路内,这样在纹路处相当于发生了砂的内部剪切现象,即砂与砂的界面剪切。④从钢-砂界面和混凝土-砂界面的试验峰值剪切应力来看,前者数值要小于后者,这与钢和混凝土本身的材料属性和表面粗糙度有关系。⑤通过界面拟合公式获取的峰值剪切应力来看,模型峰值剪切应力随着法向应力、粗糙度和粒组的变化规律和通过试验获取的相应数值的变化规律是类似的,且试验峰值剪切应力和模型峰值剪切应力的比值为0.85~0.95,说明通过双曲线模型对试验数据进行分析较合理。
|
图 6 结构物-砂剪切面形成示意图 Fig.6 Illustration of shear surface formation of interface between construction materials and sand |
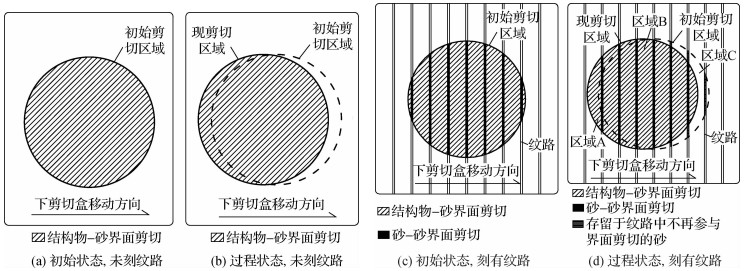
从图 6~7可以看出:①对于未刻纹路的结构物-砂界面剪切:界面剪切的初始状态如图 7(a)所示,区域D表示结构物-砂的接触区,即图中的部分,随着下剪切盒的向右移动,结构物-砂的接触区域向左移动,如图 7(b)所示,界面的剪切面因发生在结构物的表面,上剪切盒中的砂通过滑动或滚动的方式相对结构物运动,故对于未刻纹路的结构物-砂界面,其实际剪切面为一移动的水平面,如图 6中区域1所示的粗实线,对于粒组Ⅰ和粒组Ⅱ来说,实际剪切面的性状是类似的。②对于刻有纹路的结构物-砂界面剪切:界面剪切的初始状态如图 7(c)所示,区域E表示进入纹路中的砂与上剪切盒中砂的接触区域,即图中的▅部分。随着下剪切盒的向右移动,初始剪切区域相对下盒向左移动,移动到某一状态时,形成了新的剪切区域(实线圆),把实心圆与虚线圆(初始剪切区域)相交的部分定义为区域B, 把实心圆中剩余的部分定义为区域A, 把虚线圆中剩余的部分定义为区域C, 如图 7(d)所示,这样上盒中的部分砂就进入到区域A的纹路中,留在区域C纹路中的砂将不参与界面剪切,如图 7(d)中
|
图 7 结构物-砂界面剪切面构成示意图 Fig.7 Illustration of shear surface formation of interface between construction materials and sand |
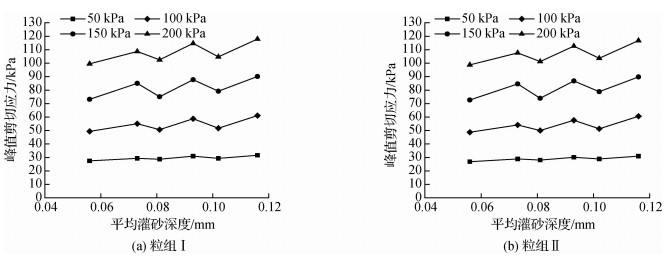
因刻有相同数量纹路的钢块和混凝土的平均灌砂深度并不相同,部分不同数量纹路的钢板和混凝土板的平均灌砂深度又比较接近,故对不同材料试块峰值剪切应力与平均灌砂深度的关系进行研究,并将两者的关系绘于图 8中。
|
图 8 结构物-砂界面峰值剪切应力与平均灌砂深度关系 Fig.8 Relationships of peak shear strength and average sand filling depth of interface between construction materials and sand |
从图 8可以看出:①粒组Ⅰ和粒组Ⅱ在同一法向应力同一灌砂深度条件下的峰值剪切应力比较接近,故两个图的规律完全一致。②在同一法向应力条件下,相同试块的峰值剪切应力随着灌砂深度的增加而增加,但不同试块的峰值剪切应力并未随灌砂深度的增加一直增加,出现交替增加和减小的现象,在50 kPa时这种现象不太明显,但随法向应力的增加这种现象愈发明显,如平均灌砂深度为0.083 mm和0.102 mm钢板的峰值剪切应力均小于平均灌砂深度为0.073 mm混凝土板的峰值剪切应力,可见界面抗剪强度与粗糙度和材料本身属性有很大关系。
2.2 界面抗剪强度指标变化规律采用Mohr-Coulomb抗剪强度破坏公式,对峰值剪切应力和法向应力关系进行线性拟合,求得界面摩擦角,如图 9和10。
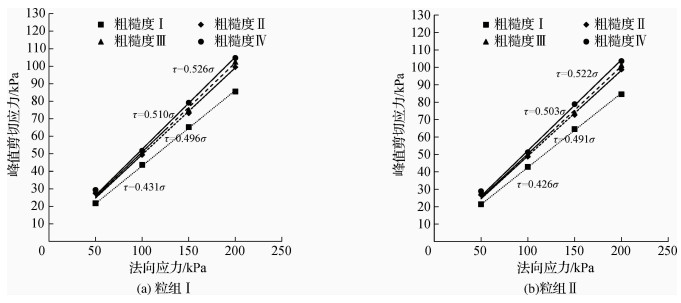
|
图 9 钢-砂界面峰值剪切应力与法向应力关系 Fig.9 Relationships of peak shear strength and normal stress of interface between steel and sand |
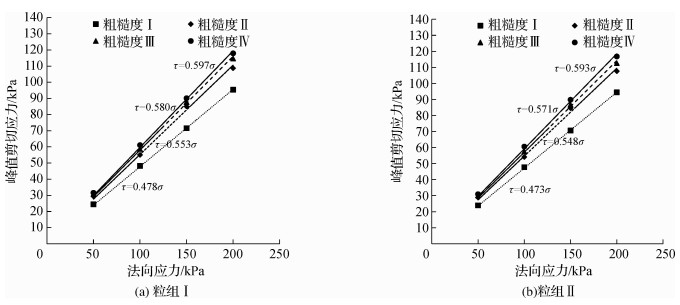
|
图 10 混凝土-砂界面峰值剪切应力与法向应力关系 Fig.10 Relationships of peak shear strength and normal stress of interface between concrete and sand |
从图 9和10可以看出:①在同一粒组条件下,界面摩擦角随粗糙度增大而增加,且界面摩擦角从粗糙度Ⅰ到粗糙度Ⅱ的增加值最大,从粗糙度Ⅱ到粗糙度Ⅳ增加较小,这与峰值剪切应力随粗糙度的变化规律一致,可见界面粗糙程度显著提高了结构物-砂界面的界面摩擦角。②在同一粗糙度条件下,粒组Ⅰ和粒组Ⅱ界面摩擦角比较接近,但是粒组Ⅰ要较粒组Ⅱ略大,这和峰值剪切应力在不同粒组下变化规律一致,其原因如前所述。③钢和混凝土两种材料的属性不同,导致两种界面的界面摩擦角有所不同,混凝土-砂界面摩擦角要大于钢-砂界面摩擦角,其中钢-砂界面摩擦角集中在23°~28°,而混凝土-砂界面摩擦角集中在25°~31°。
基于图 6~7的分析,刻有纹路的界面剪切强度由结构物-砂界面剪切强度、砂-砂界面剪切强度及结构物表面粗糙度引起的抗剪强度等三部分组成,那么界面摩擦角就被分成了三部分:区域D的摩擦角Φ1=未刻纹路界面摩擦角×区域D占总剪切面积的比例c;区域E的摩擦角Φ2=砂内剪的摩擦角×区域E占总剪切面积的比例d;结构物表面刻纹路产生的摩擦角Φ3=Φ-Φ1-Φ2。为对上述分析进行验证,分别计算刻有纹路的三部分摩擦角,如表 5所示,其中未刻纹路结构物-砂界面摩擦角为Φc,砂-砂界面摩擦角为Φd。可以看出:(1)钢-砂界面的Φ1集中在20°~23°,混凝土-砂界面的Φ1集中在22°~24°,Φ1随着粗糙度的增大而减小,因为随着粗糙度的增加,区域D的面积随之减小;粒组Ⅰ的Φ1较粒组Ⅱ的略大;混凝土-砂界面的Φ1大于钢-砂界面。(2)钢-砂界面的Φ2集中在1°~4°,混凝土-砂界面的Φ2集中在2°~4°,Φ2随着粗糙度的增大而增加,因为区域E的面积随粗糙度增加不断增大;粒组Ⅰ的Φ2较粒组Ⅱ的略小;在同一粒组同一粗糙度条件下,混凝土-砂界面的Φ2略大于钢-砂界面,因为混凝土所刻纹路的宽度略大,导致区域E略大。(3)钢-砂界面的Φ3集中在2°~4°,混凝土-砂界面的Φ3集中在2°~5°,Φ3随粗糙度的增大而增加,因为结构物表面的纹路数量随着粗糙度增加;粒组Ⅰ的Φ3与粒组Ⅱ差别不大; 钢-砂界面的Φ3小于混凝土-砂界面。
| 表 5 界面摩擦角组成 Tab.5 Composition of the interfical friction angle |
(1) 峰值剪切应力随粗糙度增大而增加,且峰值剪应力的增幅在粗糙度Ⅰ到粗糙度Ⅱ区间最大;粒组Ⅰ的峰值剪应力略大于粒组Ⅱ,因为粒组Ⅰ与粒组Ⅱ比较,其与结构物接触面积较大;混凝土-砂界面峰值剪切应力要大于钢-砂界面的对应值。
(2) 结构物-砂界面剪切应力-剪切位移关系可用双曲线模型进行描述,试验峰值剪切应力和模型峰值剪切应力的比值为0.85~0.95。
(3) 对于未刻纹路的结构物-砂界面剪切面为一移动的水平面;对于刻有纹路的结构物-砂界面剪切面由间断的水平剪切面和动态曲形剪切面构成。
(4) 界面摩擦角随粗糙度增大而增加,且在粗糙度Ⅰ到粗糙度Ⅱ区间增幅最大;粒组Ⅰ的界面摩擦角较粒组Ⅱ略大,钢-砂界面摩擦角集中在23°~28°,混凝土-砂界面摩擦角集中在25°~31°。
(5) 刻有纹路的结构物-砂界面摩擦角由未刻纹路区域的摩擦角Φ1、刻有纹路区域的摩擦角Φ2及两个区域交界处产生的摩擦角Φ3三部分组成。
| [1] |
夏红春, 周国庆. 土-结构接触面剪切力学特性及其影响因素试验[J]. 中国矿业大学学报, 2010, 39(6): 831-836. ( XIA Hongchun, ZHOU Guoqing. Experimental study of the shear mechanical characteristics at a soil-structure interface and the factors affecting them[J]. Journal of China University of Mining and Technology, 2010, 39(6): 831-836. (in Chinese)) |
| [2] |
MORTARA G, FERRARA D, FOTIA G. Simple model for the cyclic behavior of smooth sand-steel interface[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2010, 136(7): 1004-1009. DOI:10.1061/(ASCE)GT.1943-5606.0000315 |
| [3] |
田建勃, 韩晓雷, 刘江元. 砂土与混凝土接触面力学特性大型单剪试验研究[J]. 工业建筑, 2012, 42(7): 110-114. ( TIAN Jianbo, HAN Xiaolei, LIU Jiangyuan. Large-scale simple shear test on mechanical properties of interface between sandy soil and concrete face[J]. Industrial Construction, 2012, 42(7): 110-114. (in Chinese)) |
| [4] |
陆勇, 周国庆, 夏红春, 等. 接触面力学特性中相对尺度效应的试验研究[J]. 中国矿业大学学报, 2013, 42(2): 169-176. ( LU Yong, ZHOU Guoqing, XIA Chunhong, et al. Effect of relative scale to mechanical characteristics of interface[J]. Journal of China University of Mining and Technology, 2013, 42(2): 169-176. (in Chinese)) |
| [5] |
徐超, 陈洪帅, 石志龙, 等. 筋-土界面力学特性的水平循环剪切试验研究[J]. 岩土力学, 2013, 34(6): 1553-1559. ( XU Chao, CHEN Hongshuai, SHI Zhilong, et al. Research on the mechanical behavior of soil-reinforcement interface by horizontal cyclic shear test[J]. Rock and Soil Mechanics, 2013, 34(6): 1553-1559. (in Chinese)) |
| [6] |
王军, 林旭, 刘飞禹, 等. 砂土与格栅界面相互作用的直剪试验研究[J]. 岩土力学, 2014, 35(增刊1): 113-120. ( WANG Jun, LIN Xu, LIU Feiyu, et al. Research on interaction of geogrid and sand interface by direct shear tests[J]. Rock and Soil Mechanics, 2014, 35(Suppl1): 113-120. (in Chinese)) |
| [7] |
梁越, 储昊, 卢孝志, 等. 钢-土界面剪切规律时效性室内试验研究[J]. 水利水运工程学报, 2015(1): 28-32. ( LIANG Yue, CHU Hao, LU Xiaozhi, et al. Experimental studies on time effect of shearing characteristics of steel-soil interface[J]. Hydro-Science and Engineering, 2015(1): 28-32. (in Chinese)) |
| [8] |
LIU F Y, WANG P, GENG X, et al. Cyclic and post-cyclic behaviour from sand-geogrid interface large-scale direct shear tests[J]. Geosynthetics International, 2015, 23(2): 1-11. |
| [9] |
赵联桢, 陈生水, 杨东全, 等. 冻砂土-结构接触面恒温循环剪切性能研究[J]. 水利水运工程学报, 2016(1): 93-99. ( ZHAO Lianzhen, CHEN Shengshui, YANG Dongquan, et al. Cyclic shear property studies on frozen silt-structure interface under constant temperature[J]. Hydro-Science and Engineering, 2016(1): 93-99. (in Chinese)) |
| [10] |
肖杰, 屈文俊, 朱鹏, 等. 砂土与硫酸腐蚀混凝土接触面剪切试验研究[J]. 岩土力学, 2017, 38(9): 2613-2620. ( XIAO Jie, QU Wenjun, ZHU Peng, et al. Experimental study of interface shear behaviors between sand and concrete corroded by sulfuric acid[J]. Rock and Soil Mechanics, 2017, 38(9): 2613-2620. (in Chinese)) |
| [11] |
FARHADI B, LASHKARI A. Influence of soil inherent anisotropy on behavior of crushed sand-steel interfaces[J]. Soils and Foundations, 2017, 57(1): 111-125. DOI:10.1016/j.sandf.2017.01.008 |
| [12] |
GU X, CHEN Y, HUANG M. Critical state shear behavior of the soil-structure interface determined by discrete element modeling[J]. Particuology, 2017, 35: 68-77. DOI:10.1016/j.partic.2017.02.002 |
| [13] |
金子豪, 杨奇, 陈琛, 等. 粗糙度对混凝土-砂土接触面力学特性的影响试验研究[J]. 岩石力学与工程学报, 2018, 37(3): 754-765. ( JIN Zihao, YANG Qi, CHEN Chen, et al. Experimental study on effects of the roughness on mechanical behaviors of concrete-sand interface[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(3): 754-765. (in Chinese)) |
| [14] |
赵志方, 赵国藩. 采用高压水射法处理新老混凝土粘结面的试验研究[J]. 大连理工大学学报, 1999, 39(4): 558-561. ( ZHAO Zhifang, ZHAO Guofan. Experimental research on treating interface of young on old concrete with high-pressure water-jet method[J]. Journal of Dalian University of Technology, 1999, 39(4): 558-561. DOI:10.3321/j.issn:1000-8608.1999.04.019 (in Chinese)) |
| [15] |
CLOUGH G W, DUNCAN J M. Finite element analyses of retaining wall behavior[J]. Journal of the Soil Mechanics and Foundations Division, 1971, 97(12): 1657-1673. |
2. School of Highway and Architecture, Shandong Transport Vocational College, Weifang 261206, China;
3. College of Engineering, Ocean University of China, Qingdao 266100, China
 2019
2019 
