近年来,基于位移的抗震设计方法已在国外高桩码头抗震设计中大量采用[1],而且码头的易损性分析也逐渐引起研究者的关注。地震易损性分析是确定结构在不同地震动强度下发生不同破坏状态的条件概率,该方法从宏观角度描述了地震动强度对结构破坏的影响,其结果可用于地震灾害损失评估和抗震加固决策的制定[2]。对于码头的地震易损性分析,目前国外研究者开展了一些相关研究并取得了一定的研究成果。由于有关高桩码头的震害资料非常少,因此解析方法在高桩码头易损性分析中较为常用。一般通过建立码头有限元模型,采用非线性时程分析法或静力非线性分析法得到码头在不同地震动强度下的地震反应值,然后将反应值与码头不同破坏状态的定义值对比,则可以得到码头在不同地震动强度下发生不同破坏的概率,再根据破坏的概率拟合成易损性曲线。
Shafieezadeh[3]对美国西海岸一个处于液化场地的高桩码头进行了易损性分析,采用非线性时程分析法确定码头的地震需求,认为峰值地面速度作为地震强度参数较为合适,从而给出了不同构件的易损性曲线。中国台湾学者Chiou等[4]通过建立二维有限元模型对台湾的一个典型高桩码头进行了易损性分析,采用码头上部结构的横向位移作为性能指标,并将峰值地面加速度作为地震动强度参数。Yang等[5]通过建立二维数值模型研究了美国西海岸的典型全直桩码头的易损性,采用桩-上部结构连接的曲率作为性能指标。Thomopoulos等[6]采用桩-上部结构连接的曲率作为性能指标,并假定高桩码头易损性函数为两个参数的对数正态分布函数,利用极大似然估计法确定了参数的取值,建立了易损性曲线。Heidary-Torkamani等[7]采用FLAC2D建立的二维数值模型对一高桩码头进行了易损性分析,采用位移延性系数作为性能指标,同时使用谱加速度作为地震动强度参数。Amirabadi等[8]对美国西海岸的典型高桩码头进行了概率地震需求分析,对不同地震动强度参数用于需求分析的优劣进行了研究,结果表明,谱强度参数(谱加速度、谱速度、谱位移)是最佳的地震动强度参数,并采用位移延性系数和谱加速度分别作为性能指标和地震动强度参数建立了易损性曲线。Heidary-Torkamani等[2, 9]还对一设有叉桩的高桩码头进行了易损性分析,分析中分别采用位移延性系数、码头的差异沉降和残余变形作为性能指标建立了易损性曲线,并借助一次二阶矩法研究了土体力学特性不确定性对易损性曲线的影响。Shah[10]采用码头的横向位移作为性能指标,对印度主要港口的高桩码头进行了易损性分析,得到了不同设防地震动水准下的破坏概率。
从上述码头易损性分析研究不难看出,很少有研究将码头的总位移(在横向位移的基础上考虑了双向水平地震作用和扭转效应后的码头位移)作为性能指标,而基于位移的高桩码头抗震设计方法则将其作为抗震性能的指标[1]。若采用码头的总位移作为性能指标进行易损性分析,则可结合抗震设计的结果更好地评估码头的抗震性能。此外,结构的破坏状态一般采用性能指标或工程需求参数EDP(Engineering Demand Parameter)的限值定义,此时易损性就取决于工程需求参数EDP与地震动强度IM(Intensity Measure)之间的关系,而云图法和条带法[11-12]是确定二者关系的两种重要方法。上述研究中,文献[3]和[5]采用的是云图法,文献[4]和[7-10]均采用的是条带法,而文献[12]表明两种方法得到的桥梁易损性曲线有一定差别,故这两种方法对码头易损性曲线的影响有待研究。另外,文献[4]和[7-10]在易损性分析中均不考虑码头抗震能力的不确定性。针对以上问题,本文考虑分别采用云图法和条带法建立基于位移的高桩码头易损性分析方法,通过一个案例说明该方法的实施过程,同时对比分析两种方法建立的易损性曲线的差异,并研究能力不确定性对易损性曲线的影响。
1 易损性分析方法结构易损性为结构在某一地震动强度下发生某种破坏的条件概率,一般用易损性函数来表示,易损性函数的几何表示即为易损性曲线[13]。考虑到在基于位移的高桩码头抗震设计方法中,是通过比较码头的位移需求和位移能力的大小来验算抗震能力是否满足要求,即位移已作为衡量码头抗震性能的指标。故基于位移建立码头的易损性函数,即工程需求参数EDP采用结构的位移需求D来表示。在确定结构易损性函数时,一般假定结构的需求D和能力C均服从对数正态分布,则易损性函数可用下式表示[13]:
| $ P\left( {C < D|{I_{\rm{M}}}} \right) = 1 - \mathit{\Phi }\left( {\frac{{\ln {\mu _C} - \ln {\mu _D}}}{{\sqrt {\beta _C^2 + \beta _D^2} }}} \right) $ | (1) |
式中:C和D分别为码头的位移能力和位移需求,其计算方法可参考文献[1];IM为地震动强度参数;Φ(·)为标准正态分布函数;μC为码头不同极限状态对应的位移能力均值;μD为码头位移需求的均值;βC和βD分别为位移能力和位移需求的对数标准差,其中当位移能力是基于Pushover分析确定时,βC可取为0.3[13]。需要注意的是,考虑到建模的不确定性(包括材料的不确定性、有限元软件建模技术的不确定性和荷载的不确定性等)对结构反应的影响小于地震动的不确定性[14],故式(1)未考虑建模的不确定性。
采用式(1)进行码头地震易损性分析时,只需确定位移需求参数μD和βD以及μC即可。其中,位移需求参数可由概率地震需求分析确定,而μC可根据结构的极限状态通过Pushover分析近似确定。常用的确定位移需求概率模型的方法有云图法和条带法,云图法不需要对地震动记录进行调幅,而条带法则需要对地震动记录进行调幅,下文给出基于两种方法确定的易损性函数。
1.1 基于云图法的易损性函数云图法确定位移需求模型时,假定位移需求服从对数正态分布,并且位移需求D与地震动强度参数IM之间满足以下的指数关系[15]:
| $ D\left( {{I_{\rm{M}}}} \right) = aI_{\rm{M}}^b\varepsilon $ | (2) |
式中:a和b是参数,可通过回归分析确定;ε为均值为1的对数正态随机变量,且其对数标准差为βD。
对式(2)取对数可得
| $ \ln \left[ {D\left( {{I_{\rm{M}}}} \right)} \right] = \ln a + b\ln {I_{\rm{M}}} + \ln \varepsilon $ | (3) |
利用式(3)建立线性回归模型,采用最小二乘法可以得到a和b的估计值
| $ \ln {\mu _D} = \ln \hat a + \hat b\ln {I_{\rm{M}}} $ |
| $ {\beta _D} = \sqrt {\frac{{\sum\limits_{i = 1}^n {{{\left[ {\ln {D_i} - \ln {\mu _D}} \right]}^2}} }}{{n - 2}}} $ |
式中:Di为第i次非线性时程分析确定的码头位移需求;n为云图法中采用的地震动记录数目。根据确定的位移需求参数μD和βD,将其代入式(1)即可确定码头的易损性函数。
1.2 基于条带法的易损性函数采用条带法确定位移需求模型时,需将n条地震动记录调幅N次至强度IMj(j=1, 2, …, N),并对每一个地震动强度水平下的码头进行非线性时程分析以确定位移需求。同云图法一样,条带法仍假设位移需求服从对数正态分布,则在IMj下的码头位移需求概率模型为[13]:
| $ P\left( {D > d|{I_{{\rm{M}}j}}} \right) = 1 - \mathit{\Phi }\left( {\frac{{\ln d - \lambda |{I_{{\rm{M}}j}}}}{{{\beta _{D|{I_{{\rm{Mj}}}}}}}}} \right) $ | (4) |
式中:λ|IMj和βD|IMj可按下式确定:
| $ \lambda |{I_{{\rm{Mj}}}} = \ln {\mu _{D|{I_{{\rm{M}}j}}}} - \frac{1}{2}\beta _{D|{I_{{\rm{M}}j}}}^2 $ | (5) |
| $ {\beta _{D|{I_{{\rm{M}}j}}}} = \sqrt {1 + \delta _{D|{I_{{\rm{M}}\mathit{j}}}}^2} $ | (6) |
式中:μD|IMj和δD|IMj分别为位移需求D的均值和变异系数。
将由式(5)和(6)确定的lnμD|IMj和βD|IMj代入式(1)即可确定码头的易损性函数,即
| $ P\left( {C < D|{I_{{\rm{M}}j}}} \right) = 1 - \mathit{\Phi }\left( {\frac{{\ln {\mu _C} - \ln {\mu _{D|{I_{{\rm{M}}j}}}}}}{{\sqrt {\beta _C^2 + \beta _{D|{I_{{\rm{Mj}}}}}^2} }}} \right) $ | (7) |
在基于位移的码头抗震设计方法中,码头的破坏状态是根据桩身塑性铰材料应变的大小来划分的。根据文献[16]定义了3种破坏状态,如表 1所示,表中εc为混凝土应变,εs为钢筋应变,地基深处桩塑性铰指塑性铰的深度大于10倍桩径。表 1仅给出了灌注桩码头的桩塑性铰材料应变限值,对于其他桩型,可参考文献[16]。对于表 1中不同位置的塑性铰以及钢筋和混凝土的应变限值,以应变先达到限值者为准。
| 表 1 码头破坏状态 Tab.1 Damage states of wharves |
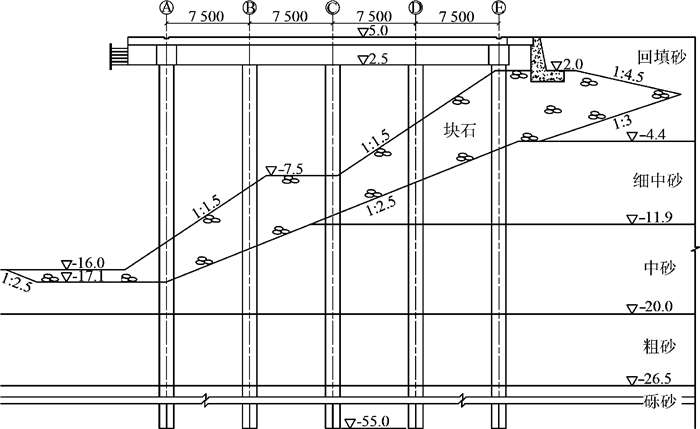
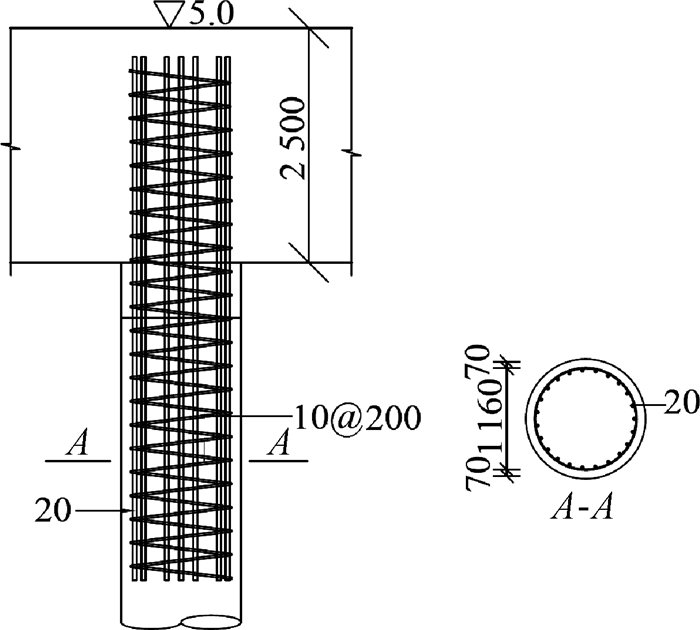
某高桩码头断面如图 1所示,码头宽34.4 m,排架间距8.0 m,分段长度112 m。面板厚0.7 m,横梁高2.5 m,宽2.0 m;轨道梁高2.5 m,宽1.8 m。码头面堆载为40 kPa,当地平均海平面为0.25 m。桩采用直径为1 300 mm的圆形实心混凝土桩(灌注桩),混凝土强度为C40,桩截面配有24根直径为20 mm的HRB400钢筋,箍筋采用HPB300,直径为10 mm,螺旋箍筋间距为200 mm,桩-上部结构连接如图 2所示。各土层物理力学参数见表 2。
|
图 1 高桩码头断面(单位:高程,m; 其他,mm) Fig.1 Transverse section of wharf (unit: elevation in m; others in mm) |
|
图 2 桩与横梁连接构造(单位:高程,m; 其他,mm) Fig.2 Details of pile-beam connection (unit: elevation in m; others in mm) |
| 表 2 各土层特性参数 Tab.2 Characteristic parameters of various soil layers |
由于码头沿其纵向对称,取一个排架进行分析。基于非线性Winkler地基上的梁模型建立码头分析模型,采用土弹簧模拟桩-土相互作用,第一个土弹簧设在坡面下15 cm处,坡面下3 m范围内间距30 cm,3 m以下范围内间距60 cm,整个建模过程在结构分析软件SAP2000内完成。土弹簧骨架曲线根据p-y曲线[17]确定,滞回模型采用软件中的Kinematic模型。采用塑性铰模拟桩的非线性特性。考虑采用分布塑性铰模型[18]代替集中塑性铰模型进而回避塑性铰长度的计算。该模型在可能出现塑性铰的位置设置多个塑性铰,塑性铰的长度取为塑性铰间距。建模过程中,将上部结构的质量和堆载(参考文献[16]考虑设计堆载的10%,即4 kPa)的换算质量等效为横梁的质量。
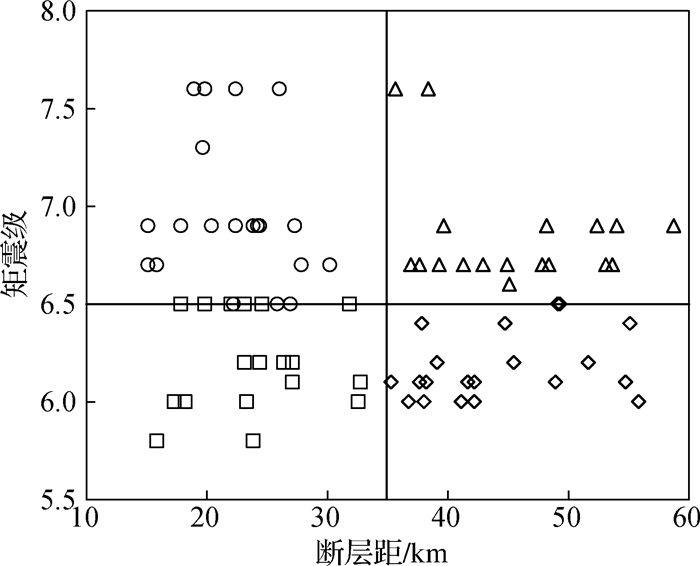
2.2 地震动记录结构易损性分析中主要考虑的不确定性包括地震动不确定性和结构不确定性。如前文所述,地震动不确定性对结构统计反应的影响要大于结构不确定性,故选择合理的地震动记录对易损性分析至关重要。选取地震动记录的方法有很多种,其中由Shome和Cornell[19]提出的选波方法在易损性分析中最为常用,其建议基于不同的Mw-R条带选取地震动记录,Mw为矩震级,R为断层距。基于Shome和Cornell的方法从美国太平洋地震工程研究中心强震数据库(PEER Ground Motion Database)选取80条地震波,此处R取为最小断层距;限于篇幅,地震波信息从略,各地震波的震级与断层距之间的关系如图 3所示。另外,不同地震动记录的峰值地面加速度aPG与断层距的关系见图 4。
|
图 3 各地震波震级与断层距之间关系 Fig.3 Relationships between Mw and R |

|
图 4 各地震波峰值地面加速度与断层距之间关系 Fig.4 Relationships between aPG and R |
对于码头位移能力均值μC,采用静力非线性Pushover分析予以确定,码头的Pushover曲线如图 5所示。码头破坏状态判断如下:Ⅰ为最小破坏,μC=2.86 cm;Ⅱ为可控且可修复的破坏,μC=8.81 cm;Ⅲ为可保障生命安全的破坏,μC=11.50 cm。

|
图 5 码头Pushover曲线 Fig.5 Pushover curve for wharf |
采用SAP2000对码头进行非线性时程分析,分析中采用前述地震动记录。由于在分析中仅针对一个排架进行计算,故时程分析的结果仅是码头的横向位移需求。为得到码头的总位移需求,根据文献[16]的规定,可将横向位移需求乘以动力放大系数fDM予以确定,其中fDM用于考虑双向水平地震作用和扭转效应的影响。fDM的计算式如下:
| $ {f_{{\rm{DM}}}} = \sqrt {1 + {{\left[ {0.3\left( {1 + 20{e_0}/{L_l}} \right)} \right]}^2}} $ | (8) |
式中:e0为码头偏心距,Ll为码头分段长度。根据本案例的条件,可得e0=11.34 m,Ll=112 m,则fDM=1.35。
对于云图法,由于无需进行地震波的调幅,因此只需进行80次时程分析,不同地震动记录的结果如图 6所示。

|
图 6 位移需求的回归分析 Fig.6 Regression analysis for displacement demands |
虽然部分研究[8]表明,谱强度参数作为地震动强度参数较好,但考虑到抗震设计中常采用aPG作为设计参数;另外,本文旨在比较不同易损性分析方法对码头易损性曲线的影响,故地震动强度参数IM采用aPG。对不同aPG下的位移需求分析结果进行回归分析,可得位移需求均值μD与aPG的关系,如式(9)所示,并可得βD=0.437 1。再根据式(1)可得码头在表 1规定的3种破坏状态下的易损性曲线
| $ \ln \left( {{\mu _D}} \right) = 1.163\ln \left( {{a_{{\rm{PG}}}}} \right) + 2.447\;1 $ | (9) |
对于条带法,由于需要调幅,考虑选取7个地震动强度水平(0.10g,0.20g,0.30g,0.40g,0.50g,0.60g和0.70g),因此需要进行80×7=560次时程分析。对于每一强度水平下的位移需求分析结果,由统计分析可得不同强度水平下的参数μD和βD(表 3)。根据式(7)可得码头在表 1规定的3种破坏状态下的易损性曲线(图 7)。
| 表 3 不同地震动强度水平下μD和βD的取值 Tab.3 Values for μD and βD under different values of aPG |

|
图 7 码头易损性曲线 Fig.7 Vulnerability curves of wharf |
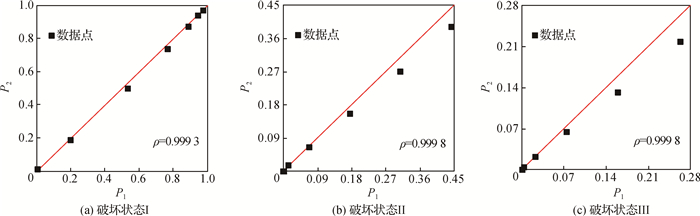
由图 7可看出,由条带法和云图法得到的易损性曲线差别不大,特别是在破坏状态Ⅰ的情况下,且随着地震动强度水平的提高,二者的差别逐渐增大;另外,条带法得到的失效概率要高于云图法,这与云图法采用回归分析方法确定位移需求均值μD有关。为分析两种方法计算结果的差异,选取7个地震动强度水平(0.10g,0.20g,0.30g,0.40g,0.50g,0.60g和0.70g)对应的概率值,如图 8所示;其中条带法和云图法的结果分别用P1和P2表示。由图 8可见,数据点紧靠45°直线。计算两组数据的相关系数,可得破坏状态Ⅰ,Ⅱ和Ⅲ下的相关系数值ρ分别为0.999 3,0.999 8和0.999 8,非常接近于1,反映出两种方法的计算结果的线性相关性非常好,与图 8中反映的情况相符,说明两种方法的计算结果相差不大。
|
图 8 云图法和条带法计算结果对比 Fig.8 Comparison between results from cloud map method and stripe method |
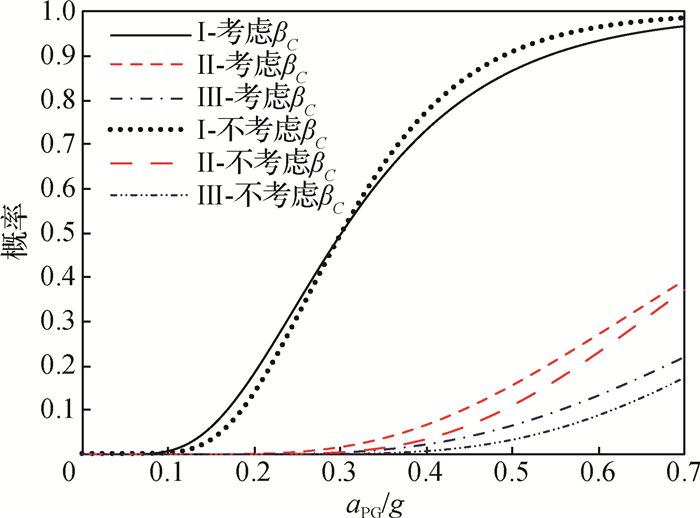
为分析位移能力不确定性对易损性曲线的影响,考虑将βC取为0,并采用云图法确定易损性曲线,图 9给出了考虑βC和未考虑βC的情况下的易损性曲线。由图 9可见,βC对曲线的影响较大,且大于易损性分析方法的影响;除破坏状态Ⅰ以外,不考虑βC会造成计算得到的失效概率偏小,不利于准确地评定码头抗震性能,故在易损性分析中应考虑位移能力不确定性的影响。为说明βC对易损性分析结果的影响大于易损性分析方法的影响,选取7个地震动强度水平对应的概率值(见表 4),其中P′2为不考虑βC的分析结果,分别计算两组数据的差值平方和。由表 4不难看出,βC对应的差值平方和要大于易损性分析方法的差值平方和,从而表明βC的影响要大于易损性分析方法的影响。
|
图 9 βC对易损性曲线的影响 Fig.9 Effects of βC on vulnerability curves |
| 表 4 不同易损性分析方法和βC的结果对比 Tab.4 Comparison between results given by various vulnerability analysis methods andβC |
通过将码头的总位移作为抗震性能指标,根据云图法和条带法分别给出了码头的易损性函数,借助一个案例阐释了基于位移的高桩码头易损性分析过程,研究了不同分析方法建立的易损性曲线的差异,分析了位移能力不确定性对易损性曲线的影响,主要得出以下结论:
(1) 基于码头的总位移建立易损性曲线,可以很好地和基于位移的高桩码头抗震设计方法相结合,从概率角度评估码头的抗震性能。
(2) 由云图法和条带法建立的码头易损性曲线差别不大,考虑到条带法需要的时程分析次数较多,故建议采用云图法建立码头的易损性曲线,但地震动记录的选取应符合一定的准则。
(3) 位移能力的不确定性对码头的易损性曲线有较大影响,在分析中应予以考虑;由于目前对于码头位移能力不确定性的研究较少,位移能力的对数标准差可近似取为0.3,但仅适用于采用Pushover分析确定码头位移能力的情况,而码头位移能力的不确定性则有待进一步深入研究。
| [1] |
高树飞, 贡金鑫, 冯云芬. 国内外高桩码头抗震性能和设计方法研究进展Ⅰ:震害和抗震设计方法[J]. 水利水运工程学报, 2016(6): 1-8. ( GAO Shufei, GONG Jinxin, FENG Yunfen. Advances in research on seismic performance and design methods for pile-supported wharves Part Ⅰ: Earthquake damage and seismic design methods[J]. Hydro-Science and Engineering, 2016(6): 1-8. (in Chinese)) |
| [2] |
HEIDARY-TORKAMANI H, BARGI K, AMIRABADI R, et al. Fragility estimation and sensitivity analysis of an idealized pile-supported wharf with batter piles[J]. Soil Dynamics and Earthquake Engineering, 2014, 61/62(2): 92-106. |
| [3] |
SHAFIEEZADEH A. Seismic vulnerability assessment of wharf structures[D]. Atlanta: Georgia Institute of Technology, 2011.
|
| [4] |
CHIOU J S, CHIANG C H, YANG H H, et al. Developing fragility curves for a pile-supported wharf[J]. Soil Dynamics and Earthquake Engineering, 2011, 31(5): 830-840. |
| [5] |
YANG C S W, DESROCHES R, RIX G. Numerical fragility analysis of vertical-pile-supported wharves in the western United States[J]. Journal of Earthquake Engineering, 2012, 16(4): 579-594. DOI:10.1080/13632469.2011.641063 |
| [6] |
THOMOPOULOS C, LAI C G. Preliminary definition of fragility curves for pile-supported wharves[J]. Journal of Earthquake Engineering, 2012, 16(Suppl1): 83-106. |
| [7] |
HEIDARY-TORKAMANI H, BARGI K, AMIRABADI R. Fragility curves derivation for a pile-supported wharf[J]. International Journal of Maritime Technology, 2013, 1(1): 1-10. |
| [8] |
AMIRABADI R, BARGI K, PIROZ M D, et al. Determination of optimal probabilistic seismic demand models for pile-supported wharves[J]. Structure and Infrastructure Engineering, 2014, 10(9): 1119-1145. DOI:10.1080/15732479.2013.793723 |
| [9] |
HEIDARY-TORKAMANI H, BARGI K, AMIRABADI R. Seismic vulnerability assessment of pile-supported wharves using fragility curves[J]. Structure and Infrastructure Engineering, 2014, 10(11): 1417-1431. DOI:10.1080/15732479.2013.823453 |
| [10] |
SHAH D. Fragility analysis of pile supported wharf using performance based design[D]. Ahmedabad: Gujarat Technological University, 2016.
|
| [11] |
于晓辉, 吕大刚. 基于云图-条带法的概率地震需求分析与地震易损性分析[J]. 工程力学, 2016(6): 68-76. ( YU Xiaohui, LÜ Dagang. Probabilistic seismic demand analysis and seismic fragility analysis based on a cloud-stripe method[J]. Engineering Mechanics, 2016(6): 68-76. (in Chinese)) |
| [12] |
MACKIE K R, STOJADINOVI B. Comparison of incremental dynamic, cloud, and stripe methods for computing probabilistic seismic demand models[C]//Proceedings of the 2005 Structures Congress and 2005 Forensic Engineering Symposium, New York, 2005.
|
| [13] |
WEN Y K, ELLINGWOOD B R, BRACCI J M. Vulnerability function framework for consequence-based engineering[R]. Urbana: University of Illinois at Urbana-Champaign, 2004.
|
| [14] |
KWON O S, ELNASHAI A. The effect of material and ground motion uncertainty on the seismic vulnerability curves of RC structure[J]. Engineering structures, 2006, 28(2): 289-303. DOI:10.1016/j.engstruct.2005.07.010 |
| [15] |
COMELL C A, JALAYER F, HAMBURGER R O, et al. Probabilistic basis for 2000 SAC federal emergency management agency steel moment frame guidelines[J]. Journal of Structural Engineering, 2002, 128(4): 526-533. DOI:10.1061/(ASCE)0733-9445(2002)128:4(526) |
| [16] |
ASCE/COPRI 61-14 Seismic design of piers and wharves [S].
|
| [17] |
API RP 2A-WSD-2005 Recommended practice for planning, designing and constructing fixed offshore platforms—working stress design[S].
|
| [18] |
CHIOU J S, YANG H H, CHEN C H. Plastic hinge setting for nonlinear pushover analysis of pile foundations[C]//The 14th World Conference on Earthquake Engineering, Beijing, 2008.
|
| [19] |
SHOME N, COMELL C A. Probabilistic seismic demand analysis of nonlinear structures[R]. Stanford: Stanford University, 1999.
|
 2019
2019 