2. 淮安市水利勘测设计研究院有限公司,江苏 淮安 223005
天然河流多为复式河槽,其断面由滩地和主槽两部分构成。枯水季节水流主要在主槽中流动,洪水季节流量大,水流漫过滩地形成漫滩水流,此时滩槽水体间的相互作用及动量交换使断面的流速分布及床面剪切应力发生变化,若直接采用曼宁公式计算过流能力则会产生很大误差。滩槽水体的相互作用使主槽行洪能力降低,滩地行洪能力增加,水流条件复杂,对防洪工程的安全产生较大影响,因此研究复式河槽的水力特性具有重要意义。
针对复式河槽水力计算的研究,吴持恭认为曼宁公式不能直接应用于复式河槽的原因在于,水流漫滩后,过水面积虽有所增加,但湿周突然增大,使水力半径骤然减小[1]。为解决该问题,Al-Khatib等[2-4]采用断面分割法将滩地与主槽分割为若干个单一断面,每个单一断面直接采用曼宁公式进行计算。由于这种方法没有考虑滩槽相互作用的能耗损失,故只能作为一种简单的估算方法。从复式河槽水流运动的内在机理出发,水流漫滩后,主槽与滩地间水体的流速差,在滩槽交界面产生了垂向漩涡,使主槽和滩地间发生动量和能量交换。由于受到水流黏性和垂向漩涡的影响,滩槽交互区的水流将发生横向运动并形成二次流。对此Shiono等[5]以水深平均的N-S方程为基础,给出了计算漫滩水流的解析公式(SKM法);杨华等[6-8]采用有限体积法对SKM模型的控制方程进行离散,得出了计算漫滩水流的数值解;刘沛清等[9-11]依据动量传递与输移理论分别提出了复式河槽过流能力的计算公式;杨克君等[12]对比分析了复式河槽流量计算的各种方法,建议在天然河道中采用河槽协同度法。Azamathulla等[13]依据线性遗传算法针对复式河槽的过流能力进行了计算,其结果与实测数据接近。这些理论方法计算准确,但结构复杂且计算量大,参数取值依赖于试验,故难以应用于实际。近年来,随着计算机技术的快速发展,数值模拟技术已经成为研究复式河槽水流运动的新方法。Costabile等[14]研究了一维洪水传播模型中滩槽间的横向动量传递作用;刘士和等[15]采用Hatchell代数应力模型,对复式河槽粗糙度沿横向存在变化的流动进行了三维模拟;槐文信等[16]结合混合有限分析法模拟了非对称断面的水流运动,得出了二次流速度矢量分布与主流流速等值线。然而这些模型仅能计算某一水位或流量下的水力要素,若计算不同水位下的过流能力,则需重新设定边界条件和初始条件,因此大大增加了计算次数,降低了计算效率。CES(Conveyance Estimation System)是由英国Wallingford水力研究公司开发的一款用于计算河道断面水流的软件,因操作简单、计算准确而广泛应用于河道水力计算[17-19]。
本文应用CES模型计算不同复式河槽的垂线平均流速,并以英国科学工程研究理事会洪水水槽设备(SERC-FCF)的试验资料为验证依据,首先讨论该模型在复式河槽水力计算中的适用性;然后对比不同方法计算复式河槽过流能力的精度,论证CES模型在复式河槽水力计算中的优越性。
1 计算方法计算复式河槽流量主要有经验方法(湿周修正法、断面分割法)和理论方法(谢汉祥法、刘沛清法、河槽协同度法),具体见文献[20]。本文主要介绍CES模型法。
CES模型以沿水深平均的Navier-Stokes方程为基础,综合考虑了床面摩阻力、二次流及滩槽动量交换对过流能力的影响。其控制方程[21]为:
| $ g H S_{0}-\frac{f q^{2}}{8 H^{2}}\left(1+\frac{1}{s^{2}}\right)^{1 / 2}+\frac{\partial}{\partial y}\left(\lambda H\left(\frac{f}{8}\right)^{1 / 2} q \frac{\partial}{\partial y}\left(\frac{q}{H}\right)\right)=c_{1} \Gamma+c_{2} C_{\mathrm{uv}} \frac{\partial}{\partial y}\left(\frac{q^{2}}{H}\right) $ | (1) |
| $ c_{1}=\frac{(1.1-s)}{0.1}, c_{2}=\frac{(\sigma-1.0)}{0.1} ; 1.00 \leqslant \sigma \leqslant 1.10 $ | (2) |
| $ c_{1}=0, c_{2}=1 ; \sigma>1.10 $ | (3) |
式中:g为重力加速度;H为水深;S0为河道纵坡;f为床面阻力系数;q为单宽流量;s为河道边坡坡度;y为断面横向坐标;λ为无量纲涡黏性系数;σ为河槽弯曲度,顺直河槽σ=1.00;Cuv为河槽弯曲度σ的函数;Γ为二次流影响因子。
对CES模型的控制方程采用有限元法求解。首先以河槽横断面为求解域,将其离散为E个宽度为Δy的计算单元。将式(4)代入式(1),把变量q替换为Δqn,使控制方程线性化,再利用设定的线性分段函数Δqn(y)近似表示计算单元上的未知函数,最后通过迭代计算及设定的边界条件(q=0)求出线性方程组的解。
| $ q_{n+1}=q_{n}+\chi \Delta q_{n} $ | (4) |
式中:χ为松弛因子,取值范围为0~1.5;Δqn为增量;n为迭代次数。f,λ,Γ,Cuv为CES模型的基本参数,由式(5)~(8)确定。
| $ \frac{1}{{\sqrt f }} = \mathit{c}lg\left[ {\frac{{{k_{\rm{s}}}}}{{aH}} + \frac{{bq}}{{4v\sqrt f }}} \right] $ | (5) |
| $ \lambda = {\lambda _{{\rm{mc}}}}\left( { - 0.2 + 1.2D_{\rm{r}}^{ - 1.44}} \right), 0.07 < {\lambda _{{\rm{mc}}}} < 0.5 $ | (6) |
| $ {\mathit{\Gamma }_{{\rm{mc}}}} = 0.15\mathit{H}\rho g{\mathit{S}_0};{\Gamma _{{\rm{fp}}}} = - 0.25\mathit{H}\rho g{\mathit{S}_0} $ | (7) |
| $ C_{\mathrm{uv}}=7.1659 \sigma-6.6257 $ | (8) |
式中:ks为绝对粗糙度;a, b, c分别为河槽形状系数;λmc为主槽区无量纲涡黏性系数; Γmc为主槽区二次流影响因子; Γfp为滩地区二次流影响因子; υ为运动黏滞系数;Dr为相对水深,即当前位置水深与最大水深之比。
引入归一化均方根误差e来直观比较各种方法在计算过流量时的精度,e的值越接近0,说明计算精度越高;越接近1,则精度越低。其计算式如下:
| $ e = \sqrt {\frac{1}{m}\sum\limits_{i = 1}^m {{{\left( {{Q_{测}} - {Q_{计}}} \right)}^2}} /\left( {{Q_{测}} - {Q_{计}}} \right)} $ | (9) |
式中:Q测为流量实测值;Q计为流量计算值;m为数据组数。
2 结果与分析为对比上述各方法在计算过流能力时的精度,以及讨论CES模型在不同复式河槽水力计算中的适用性,采用英国科学工程研究理事会洪水水槽设施(SERC-FCF)的试验资料进行验证。具体参数见表 1。
| 表 1 不同复式河槽断面形态参数 Tab.1 Cross-section morphology parameters of different compound channels |
为验证CES模型在计算复式河槽流速分布中的适用性,并讨论主槽边坡系数及滩地宽度对复式河槽流速分布的影响,利用该模型分别计算不同河槽在不同水深下的垂线平均流速,其结果如图 1所示。

|
图 1 不同复式河槽在不同水深下的垂线平均流速分布 Fig.1 Average velocity distribution of different water depths in compound channels |
由图 1可见,对于任意形态的复式河槽,CES模型的计算结果与实测值十分吻合,说明该模型能适用于复式河槽的水力计算。另外,还可发现以下规律:
(1) 对于任一河槽,主槽流速大于滩地流速。随着水深增加,滩槽区流速差逐渐减小,断面流速分布趋于均匀化,说明滩槽水体间的动量交换随水深的增加不断增强,水体间的相互混掺与碰撞加大了交界处的紊流强度,进而使断面流速分布逐渐均匀。
(2) 滩槽交界处的流速梯度最大,主槽中心区和远离交界处的滩地区,其流速分布较为均匀。依此将河槽划分为滩槽交互区、主槽平衡区及滩地平衡区,由此可见滩槽水体的动量交换强度还与断面位置有关,离滩槽交界处的距离越近,其动量交换作用越大,反之则越小。
(3) 对比图 1(a)和(c)发现同一水深条件下,两个河槽的流速大小与分布都较为接近,因此可忽略主槽边坡系数对复式河槽水力特性的影响。由图 1(a)和(b)可见,两个滩地宽度不同的河槽在主槽平衡区及滩槽交互区的流速分布较为接近,而在滩地平衡区差别较大。这将直接影响主槽滩地的分流比,即同一水深条件下,滩地越宽,分流比越小,滩地过流量越大。
2.2 不同方法流量结果的对比分析按照前述方法分别计算不同形态水槽的水位流量关系,并结合实测值按式(9)计算对应的e值,再将不同方法的计算结果与实测值比较(见表 2),以评价各方法的计算精度。
| 表 2 不同方法计算不同形态河槽的误差 Tab.2 Error values given by different methods for different compound channels |
由表 2可见,对于任意形态的复式河槽,刘沛清法计算的流量精度最差,其误差值达到其他方法的3倍以上。湿周修正法的计算结果精度较差,这是因为该方法将滩槽水体相互作用时的能耗损失简单转化为湿周长度的变化,而忽略了滩槽间动量交换对过流能力的影响,故该方法的计算结果小于实测值。谢汉祥法与河槽协同度法的计算结果总体上与实测值较为接近。谢汉祥法须分别计算主槽与滩地的过流能力,而后根据叠加原理得出整个断面的过流量;协同度法中的流量校正因子随水深的增加会发生复杂的变化,计算时应根据水深进行分区计算,因此谢汉祥法与协同度法在计算河槽过流能力时较为复杂。
断面分割法计算复式河道的过流能力是现实中采用较多的一种方法。表 2中3种分割法计算结果的精度均较高,这是因为主槽平衡区与滩地平衡区的流速分布较为均匀(如图 1),接近均匀流,因此将滩槽分割后分别采用曼宁公式计算,其结果较为准确。由于水平分割法忽略了滩槽间的表观切应力,故其结果小于实测值;垂直分割法与对角线分割法均考虑了滩槽间的表观切应力,而垂直分割法的精度远小于对角线分割法,这说明复式断面上存在一条零切应力线,且这条线大致沿对角线方向,故对角线分割法精度较高。
CES模型与其他方法相比,在任意形态断面的过流能力计算结果中精度最高。这是因为模型的控制方程以流体力学基本方程(Navier-Stokes方程)为基础,综合考虑了滩槽间的动量交换、二次流以及断面形状对过流能力的影响,故其计算结果与实测结果差别最小。此外,该方法还具有操作简单、耗时短、通用性强的优点。
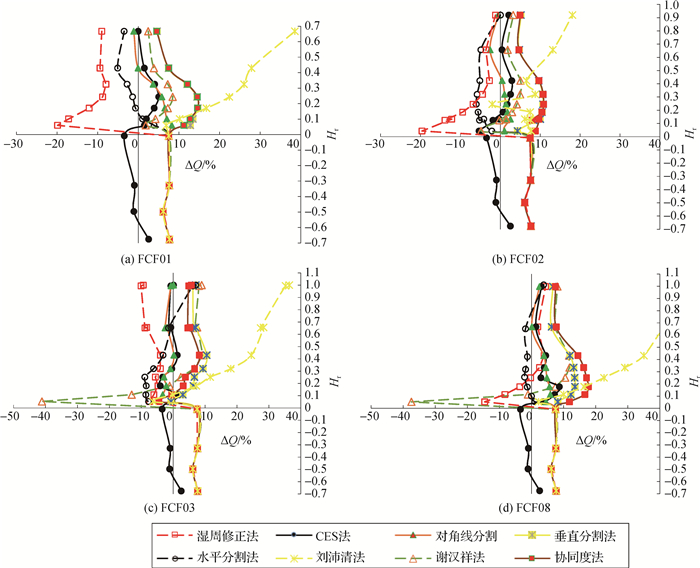
图 2为不同形态河槽的不同方法计算结果与实测值的偏差随水深的变化。
|
图 2 不同方法计算不同形态河槽的计算与实测值偏差随水深变化 Fig.2 Difference between calculated and measured values varying with water depth in different compound channels |
图 2中横坐标ΔQ=(Q计-Q测)/Q测×100%为不同方法计算结果与实测值的偏差,纵坐标Hr=(H-h)/h为相对水深,直线ΔQ=0为实测值。不同方法的计算结果与该直线越接近,则精度越高,反之就越低。由图 2可见,水流漫滩之前,即Hr < 0时,各种经验方法与理论方法的计算偏差均相同。这是因为水体只在主槽中流动而不受滩地影响,体现动量交换的各参数均为零。简化后,这些方法均为曼宁公式。对比各种方法在水流漫滩前的计算结果发现,CES模型的计算精度较高,其原因在于CES模型的控制方程是由液体运动的基本方程(N-S方程)推导而来,而且数值解与实测值更为接近;曼宁公式虽是经典的水力学计算公式,但毕竟是经验性公式,因此其结果的偏差相对较大。
由图 2还可见,水流漫滩后,刘沛清法计算结果的偏差度随水深增加而增大,这是因为该方法计算水位流量关系时,体现滩槽水体间的动量传递的输运系数α未能考虑水深变化对动量交换的影响,因此计算偏差逐渐增大。水流漫滩初期,采用湿周修正法计算断面过流能力时,滩地宽度较大的FCF01,FCF02,FCF08断面精度较低,滩地较小的FCF03断面精度较高,其原因在于滩地宽度越大,滩地对整个断面过流能力的影响也越大。而该方法将滩槽水体相互作用产生的能耗损失简单转化为湿周长度的变化,忽略了滩槽间动量交换对过流能力的影响,因此滩地宽度越大,精度越低。其他方法计算结果的偏差主要随水深的变化而变化,水流在漫滩初期滩槽交互区的流速梯度最大,而这些方法的经验参数很难准确反映这种复杂的水力特性,故计算偏差相对较大;随着水深的增加,滩槽水体的相互作用逐渐减小,流速分布趋于均匀,因此计算偏差也随之减小。通过对比不同方法的计算结果,总体上看CES模型的计算精度依然最高,且计算结果的偏差随水深的变化相对较小。由此可见,不论水流是否漫滩,CES模型不失为复式河槽水力计算的最优方法。
3 结语应用CES模型分别计算了不同形态复式河槽的过流能力和垂线平均流速,并采用已有试验资料对其进行了验证,进而分析了不同形态复式河槽的水流特性;然后对比了不同方法计算过流能力的精度,论证了CES模型在水力计算中的优越性,由此得出了以下主要结论:
(1) 对任意形态的复式河槽,CES模型计算的垂线平均流速分布与实测值吻合较好,可直接应用于复式河槽的水力计算。
(2) 滩槽水体间的动量交换强度随水深的增加而增大,水体间相互混掺与碰撞增大了交界处的紊流强度,使断面流速分布趋于均匀;滩槽水体的动量交换强度还与断面位置有关,在滩槽交界处最大,离交界处距离越远,动量交换作用越小。
(3) 滩地宽度直接影响主槽滩地的分流比,滩地宽度越大,分流比越小,同一流量下河槽水位越低;主槽边坡系数对复式河槽水力特性的影响可忽略。
(4) 与其他方法相比,CES模型计算流量的精度高且适用性强,加之计算快捷,操作简单,是计算复式河槽过流能力的优选方法。
| [1] |
吴持恭. 水力学[M]. 北京: 高等教育出版社, 2016. ( WU Chigong. Hydraulics[M]. Beijing: Higher Education Press, 2016. (in Chinese))
|
| [2] |
AL-KHATIB I A, DWEIK A A, GOGUS M. Evaluation of separate channel methods for discharge computation in asymmetric compound channels[J]. Flow Measurement and Instrumentation, 2012, 24(1): 19-25. |
| [3] |
ZENG Y H, GUYMER I, SPENCE K J, et al. Application of analytical solutions in trapezoidal compound channel flow[J]. River Research and Applications, 2012, 28(1): 53-61. |
| [4] |
WORMLEATON P R, ALLEN J, HADJIPANOS P. Discharge assessment in compound channel flow[J]. Journal of Hydraulic Division, 1982, 108(9): 975-994. |
| [5] |
SHIONO K, KNIGHT D W. Turbulent open-channel flows with variable depth across the section[J]. Journal of Fluid Mechanics, 1991, 222(1): 617-646. |
| [6] |
杨华, 廖华胜, 李连侠, 等. SKM模型在天然河道的适用性研究[J]. 水利水电科技进展, 2011, 31(3): 53-56. ( YANG Hua, LIAO Huasheng, LI Lianxia, et al. Applicability of SKM model in natural channels[J]. Advances in Science and Technology of Water Resource, 2011, 31(3): 53-56. (in Chinese)) |
| [7] |
芦妍婷, 刘达, 李连侠, 等. 不同形状断面河槽下SKM模型解析解与数值解的比较分析[J]. 广东水利水电, 2012(7): 3-6. ( LU Yanting, LU Da, LI Lianxia, et al. Comparison and analysis of analytic solution of SKM model and numerical solution in different compound channels[J]. Guangdong Water Resources and Hydropower, 2012(7): 3-6. DOI:10.3969/j.issn.1008-0112.2012.07.002 (in Chinese)) |
| [8] |
刘达, 芦妍婷, 李连侠, 等. 明渠流动S-K模型在具有垂直壁面的复式断面下的数值模拟[J]. 武汉大学学报(工学版), 2012, 45(2): 148-151, 156. ( LIU Da, LU Yanting, LI Lianxia, et al. Numerical simulation of SKM in open-channel with vertical wall[J]. Engineering Journal of Wuhan University, 2012, 45(2): 148-151, 156. (in Chinese)) |
| [9] |
刘沛清, 冬俊瑞. 复式断面渠道中均匀流的水力计算[J]. 长江科学院院报, 1995, 12(3): 61-66. ( LIU Peiqing, DONG Junrui. Hydraulic calculation of uniform flow in compound channel[J]. Journal of Yangtze River Scientific Research Institute, 1995, 12(3): 61-66. (in Chinese)) |
| [10] |
谢汉祥. 漫滩水流的简化计算[J]. 水利水运科学研究, 1982(2): 84-92. ( XIE Hanxiang. Simplified calculation of water flow in floodplain[J]. Journal of Nanjing Hydraulic Research Institute, 1982(2): 84-92. (in Chinese)) |
| [11] |
王韦.弯曲河道水沙运动规律及顺直复式河槽流量分配[D].成都: 成都科技大学, 1989. (WANG Wei. The movement law of curved river water sediment and the flow distribution of straight compound channel[D]. Chengdu: Chengdu University of Science and Technology, 1989. (in Chinese))
|
| [12] |
杨克君, 曹叔尤, 刘兴年, 等. 复式河槽流量计算方法比较与分析[J]. 水利学报, 2005, 36(5): 563-568. ( YANG Kejun, CAO Shuyou, LIU Xingnian, et al. Comparison of methods for calculating flow capacity of channels with compound cross section[J]. Journal of Hydraulic Engineering, 2005, 36(5): 563-568. DOI:10.3321/j.issn:0559-9350.2005.05.009 (in Chinese)) |
| [13] |
AZAMATHULLA H M, ZAHIRI A. Flow discharge prediction in compound channels using linear genetic programming[J]. Journal of Hydrology, 2012, 454. |
| [14] |
COSTABILE P, MACCHIONE F. Analysis of one-dimensional modelling for flood routing in compound channels[J]. Water Resources Management, 2012, 26(5): 1065-1087. DOI:10.1007/s11269-011-9947-2 |
| [15] |
刘士和, 黄伟, 罗秋实. 复式明渠水流运动的数值模拟[J]. 武汉大学学报(工学版), 2006, 39(6): 1-5. ( LIU Shihe, HUANG Wei, LUO Qiushi. Numerical simulation of compound open channel flow[J]. Engineering Journal of Wuhan University, 2006, 39(6): 1-5. (in Chinese)) |
| [16] |
槐文信, 梁爱国, 杨中华, 等. 非对称复式断面明渠水流特性试验与数值模拟[J]. 华中科技大学学报(自然科学版), 2007, 35(12): 95-98. ( HUAI Wenxin, LIANG Aiguo, YANG Zhonghua, et al. Experimental and numerical study on behavior of flow in a unsymmetrical compound channel[J]. Journal of Huazhong University of Science and Technology(Natural Science Edition), 2007, 35(12): 95-98. DOI:10.3321/j.issn:1671-4512.2007.12.027 (in Chinese)) |
| [17] |
胡红胜.顺直型复式河道断面的水力学特性研究[D].西安: 西安理工大学, 2016. (HU Hongsheng. Study on hydraulic characteristics in straight compound channel[D]. Xi'an: Xi'an University of Technology, 2016. (in Chinese)) http://cdmd.cnki.com.cn/Article/CDMD-10700-1017731917.htm
|
| [18] |
DAS B S, KHATUA K K, DEVI K. Numerical solution of depth-averaged velocity and boundary shear stress distribution in converging compound channels[J]. Arabian Journal for Science and Engineering, 2017, 42(3): 1305-1319. DOI:10.1007/s13369-016-2382-1 |
| [19] |
AKTER A, CRAPPER M, PENDER G, et al. Performance of a geobag revetment II: numerical modeling[J]. Journal of Hydraulic Engineering, 2013, 139(8): 877-885. DOI:10.1061/(ASCE)HY.1943-7900.0000724 |
| [20] |
杨坡, 魏炳乾, 胡红胜, 等. 复式河槽水位流量计算误差分析及方法对比[J]. 水利水运工程学报, 2019(1): 94-101. ( YANG Po, WEI Bingqian, HU Hongsheng, et al. Error analysis and method comparison for calculating stage-discharge relation in compound channel[J]. Hydro-Science and Engineering, 2019(1): 94-101. (in Chinese)) |
| [21] |
Conveyance Estimation System. Reducing uncertainty in river flood conveyance, Phase 2 conveyance manual[M]. UK: Environment Agency, 2004.
|
2. Designing and Research Institute of Water Conservancy Investigation in Huai'an, Huai'an 223005, China
 2019
2019