2. 黄河水利委员会黄河水利科学研究院,河南 郑州 450003;
3. 华北水利水电大学,河南 郑州 450045;
4. 纽卡斯尔大学 建筑环境与工程系,新南威尔士 纽卡斯尔 2308
黄河河道整治工程中险工坝岸常用散抛石护根,以维护坝垛与河岸的安全。坝垛工程的稳定直接影响到堤防安全,而坝岸根石护坡的稳定性又直接决定了坝岸工程的稳定性。在河道整治过程中,水下块石在水流作用下的受力情况分析大多来自于工程经验总结[1-4],缺少科学理论依据。研究水下块石的受力情况,水流作用块石的拖曳力是重要的力学参数[5]。目前针对球体或二维圆柱体水平拖曳力有较为成熟的计算公式,其水平拖曳力与作用流速的平方、垂直水流方向的投影面积成正比,拖曳力系数采用经验值或试验值[6-10]。缑元有[11]利用水平拖曳力公式分析河道整治工程根石受力状态, 建立了根石走失的物理模型;庞启秀等[12-13]通过水槽试验测量了水流作用下不同尺度大颗粒块体受到的水平拖曳力,研究了块体形状对水流拖曳力的影响。但目前对于不同形状物体拖曳力系数的研究还不够充分,多将块体近似为等体积球体[14],采用球体拖曳力系数的经验值[15],这是不够准确的。对于近似长方体或正方体物体,不同于球体或流线型体的流体分离,流经具有折角的块体的流体分离形式由块体形状决定。Hoerner[16]综合了不同研究者关于长方体拖曳力系数随长高比变化关系,Evett等[17]给出块体形状雷诺数大于1 000时的拖曳力系数随宽高比变化关系。近年来数值模拟软件FLOW-3D[18-19]广泛应用于工程,在水力学方面取得了良好的效果。本文通过物理试验,发现块体拖曳力大于同体积的球体拖曳力,故在物理试验基础上,运用数值模拟软件FLOW-3D,进一步验证和探索水下块体拖曳力与不同块体尺寸之间的关系,对比了近似体积块体和球体之间水平拖曳力和水平拖曳力系数,分析了块体不同宽高比、长高比以及块体与水流夹角对水平拖曳力系数的影响。为进一步研究垛坝根石冲揭失稳提供依据,也为黄河河道整治工程提供数值模拟参考。
1 数值模型 1.1 水流控制方程FLOW-3D软件将N-S方程作为不可压缩流体运动的控制方程。该软件采用矩形网格单元,并且加入了面积分数和体积分数,控制方程基于笛卡尔坐标系建立。
连续方程:
| $ \frac{\partial\left(u A_{x}\right)}{\partial x}+\frac{\partial\left(v A_{y}\right)}{\partial y}+\frac{\partial\left(w A_{y}\right)}{\partial z}=0 $ | (1) |
动量方程:
| $ \frac{\partial u}{\partial t}+\frac{1}{V_{\mathrm{F}}}\left\{u A_{x} \frac{\partial u}{\partial x}+v A_{y} \frac{\partial u}{\partial y}+w A_{z} \frac{\partial u}{\partial z}\right\}=-\frac{1}{\rho} \frac{\partial p}{\partial x}+G_{x}+f_{x} $ | (2) |
| $ \frac{\partial v}{\partial t}+\frac{1}{V_{\mathrm{F}}}\left\{u A_{x} \frac{\partial v}{\partial x}+v A_{y} \frac{\partial v}{\partial y}+w A_{z} \frac{\partial v}{\partial z}\right\}=-\frac{1}{\rho} \frac{\partial p}{\partial y}+G_{y}+f_{y} $ | (3) |
| $ \frac{\partial w}{\partial t}+\frac{1}{V_{\mathrm{F}}}\left\{u A_{x} \frac{\partial w}{\partial x}+v A_{y} \frac{\partial w}{\partial y}+w A_{z} \frac{\partial w}{\partial z}\right\}=-\frac{1}{\rho} \frac{\partial p}{\partial z}+G_{z}+f_{z} $ | (4) |
式中:u,v,w为x,y,z方向的流速分量;Ax,Ay,Az为流体流经单元的截面面积比例;Gx,Gy,Gz为x,y,z方向的流体加速度;fx,fy,fz为x,y,z方向上的黏滞力加速度;VF为流体流经计算单元的体积分数;ρ为流体密度;p为作用在流体微元上的压强。
1.2 紊流模型FLOW-3D中提供了多种紊流模型的选择,RNG k-ε[20]紊流模型被广泛应用于复杂水流的模拟。紊流模型的控制方程如下。
紊动能k方程:
| $ \frac{\partial(\rho k)}{\partial t}+\frac{\partial\left(\rho k u_{i}\right)}{\partial x_{i}}=\frac{\partial}{\partial x_{j}}\left[\left(\mu+\frac{\mu_{t}}{\sigma_{k}}\right)\right]+G_{k}+\rho \varepsilon $ | (5) |
紊动能耗散率ε方程:
| $ \frac{{\partial (\rho \varepsilon )}}{{\partial t}} + \frac{{\partial \left( {\rho \varepsilon {u_i}} \right)}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + \frac{{{\mu _{\rm{t}}}}}{{{\sigma _\varepsilon }}}} \right)\frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right] + \frac{{C_{1\varepsilon }^*}}{k}{G_k} - {C_{2\varepsilon }}\frac{{{\varepsilon ^2}}}{k} $ | (6) |
| $ \left\{ {\begin{array}{*{20}{c}} {{G_k} = {\mu _1}\left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right)\frac{{\partial {u_i}}}{{\partial {x_j}}}}\\ {C_{1\varepsilon }^* = {C_{1\varepsilon }} - \frac{{\eta \left( {1 - \eta /{\eta _0}} \right)}}{{1 + \beta {\eta ^3}}}}\\ {\eta = {{\left( {2{E_{ij}} \cdot {E_{ij}}} \right)}^{1/2}}\frac{k}{\varepsilon }}\\ {{E_{ij}} = \frac{1}{2}\left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right)} \end{array}} \right. $ | (7) |
式中:k为紊动能;ε为紊动能耗散率;μ为紊动黏滞系数;μt为紊动的运动黏滞系数,μt=Cμk2/ε,Cμ=0.085;σk=σε=0.717 9;Eij为流体应变率; Gk是紊动能k的产生项;C1ε=1.42;C2ε=1.68;η0=4.377;β=0.012。
1.3 VOF法VOF法是Hirt等[21]在1981年提出的追踪自由液面的方法。在对比了多种方法后发现VOF法在有限差分法计算中最能有效模拟液面的自由变化过程,其基本原理为通过研究网格单元中流体和网格体积比函数F来确定自由液面,F的输运函数为:
| $ \frac{\partial F}{\partial t}+\frac{1}{V_{\mathrm{F}}}\left[\frac{\partial\left(F A_{x} u\right)}{\partial x}+\frac{\partial\left(F A_{y} v\right)}{\partial y}+\frac{\partial\left(F A_{z} w\right)}{\partial z}\right]=0 $ | (8) |
FLOW-3D采用了FAVOR技术[22](Fractional Area/Volume Obstacle Representation)来定义计算区域。FAVOR技术也称网格和几何体相互独立的自由网格法,在网格内部定义物体的几何形状,同时在计算过程中,根据计算结果自行调整所描述物体的几何形状,可以达到利用简单矩形网格来描述复杂几何模型的目的。
1.5 水平拖曳力公式淹没于水流中的物体受到水流作用力。对于球体或圆柱体受到的水平作用力,Evett等[17]提出水平拖曳力公式:
| $ F_{\mathrm{D}}=\frac{1}{2} \rho C_{\mathrm{D}} A U^{2} $ | (9) |
式中:FD为水流拖曳力;CD为拖曳力系数;ρ为流体密度;U为水流流速;A为块体在垂直于来流方向的投影面积。
由式(9)变化可得到拖曳力系数CD的表达式:
| $ C_{\mathrm{D}}=\frac{F_{\mathrm{D}}}{\frac{1}{2} \rho A U^{2}} $ | (10) |
物理试验系统由变坡水槽、流速仪、电阻式压力传感器、滑轮支架、四通道信号转换器、WiFi无线传输器等设备组成(见图 1)。该系统可实现块体周边流速、块体受水流的水平与垂直压力、各点水压力的实时在线量测与传输, 满足水流流速与块体受力的同步不间断量测,获取水流瞬时流速、时均流速、块体水平压力与垂向压力等数据。

|
图 1 物理试验布置 Fig.1 Layout of physical experiments |
实地量测黄河花园口险工122#坝、马渡险工25#坝及九堡险工118#坝根石尺寸,根石块体的宽高比为1.01~2.55,长高比为1.29~3.40。试验块体具有多种尺寸,顺水流方向的是块体长度L,迎水面分别是块体的宽B和高S,具体尺寸见表 1,满足实际长高比和宽高比要求。模型块体尺寸与试验尺寸一致,模型尺寸与实际工程尺寸比例大约为1/4~1/10。
| 表 1 块体尺寸参数 Tab.1 Size parameters of blocks |
建立简单的数值水槽,水槽长3.0 m,宽0.6 m。固定块体放置在水槽的中部位置,块体中心距离水槽底部0.12 m。小槽采用0.015 m×0.015 m×0.015 m的矩形结构化网格,对块体采用0.01 m×0.01 m×0.01 m的矩形网格加密,网格总数约为20万个。模型布置和网格划分如图 2。

|
图 2 模型布置和网格划分 Fig.2 Model layout and mesh generation |
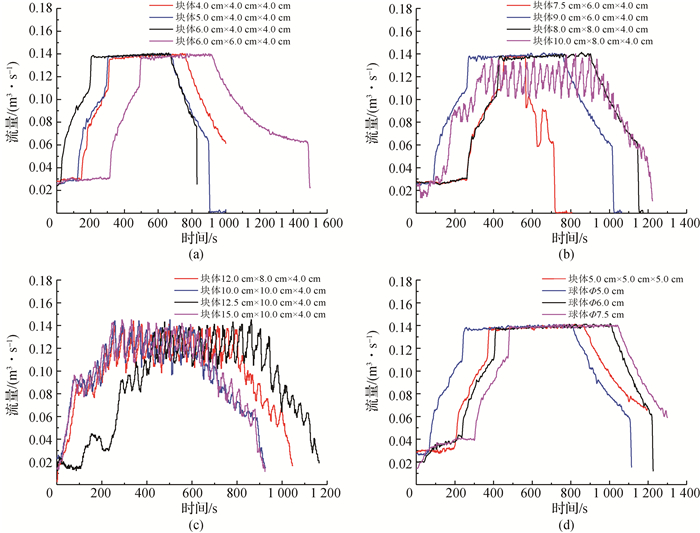
入口边界为流量边界,入口流量为物理试验流量(见图 3),出口是水位为0.25 m的压力边界,左右及底面是固壁边界,计算区域的上方为标准大气压,计算区域内的初始水位为0.25 m。计算时间步长与数据采集的时间步长一致,设置为2 s。并且设置一道baffle用以观察模拟过程中流量的变化。
|
图 3 入口流量曲线 Fig.3 Discharge curves at inlet |
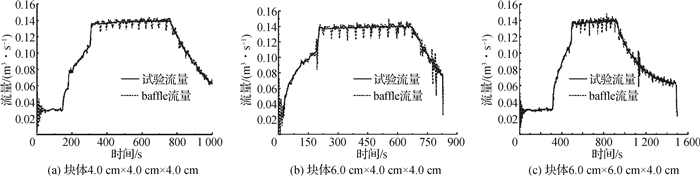
通过试验流量与模拟baffle记录流量的对比,验证数值模拟初始设置的可靠性。因模拟数量过多,所以选取几个模拟流量进行对比。块体4.0 cm×4.0 cm×4.0 cm,6.0 cm×4.0 cm×4.0 cm,6.0 cm×6.0 cm×4.0 cm的试验流量和baffle流量对比见图 4。结果表明,R2为0.994,说明baffle记录流量与试验流量基本吻合。这证明数值模拟初始设置可行。
|
图 4 Discharge curves at inlet Fig.4 Comparison between curves of block experimental discharge and baffle discharge |
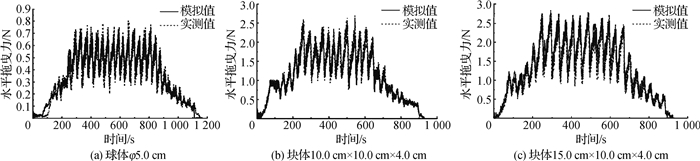
选取球体φ5.0 cm和块体10.0 cm×10.0 cm×4.0 cm,15.0 cm×10.0 cm×4.0 cm在水流作用下水平拖曳力的模拟值与实测值进行对比,以验证计算结果的准确性。水平拖曳力对比曲线如图 5所示。结果表明,R2约为0.94,水平拖曳力的模拟值与实测值基本吻合。这说明所建模型计算的拖曳力比较准确。
|
图 5 块体水平拖曳力 Fig.5 Block horizontal drag force |
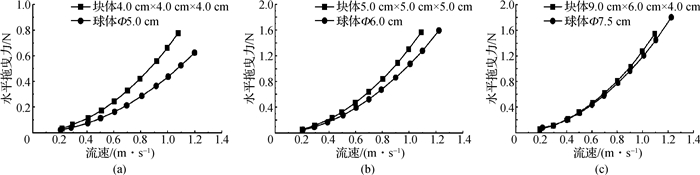
块体与近似体积球体的水平拖曳力和水平拖曳力系数对比见图 6和7。从图 6和7中可以很明显看出块体的水平拖曳力大于球体的水平拖曳力,其中块体的水平拖曳力系数更是球体水平拖曳力系数的1.5~2.0倍。如将水下块体近似等体积球体,计算出水流作用下的水平拖曳力值偏小。
|
图 6 块体与球体水平拖曳力对比曲线 Fig.6 Comparison curves between horizontal drag force of blocks and sphere |
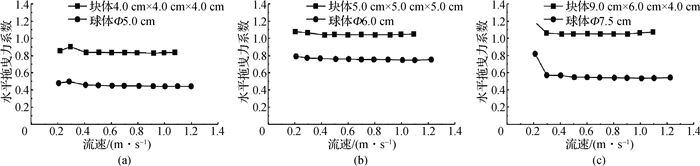
|
图 7 块体与球体水平拖曳力系数对比曲线 Fig.7 Comparison curves of horizontal drag force coefficients of blocks and sphere |
从图 6的流速与水平拖曳力的关系曲线可以看出,水平拖曳力与流速的平方成正比。从图 7的变化曲线可以得出:(1)水流流速低于0.4 m/s时,块体周围的流场处于不稳定状态,水平拖曳力系数也处于变化之中,与物理模型试验相符合;(2)流速大于0.4 m/s时,水平拖曳力系数趋于稳定,球体水平拖曳力系数为0.4~0.8,块体水平拖曳力系数为0.8~1.1,与Evett等[17]的研究结果(CD=1.05)相近。
4.2 块体尺寸对水平拖曳力系数的影响块体不同于球体,块体具有各向异性、边界棱角不规则特性,块体迎水面的宽高比和侧面的长高比将会直接影响水流对块体的作用力。为研究块体尺寸对水平拖曳力系数的影响,对比分析不同宽高比、长高比与水平拖曳力系数的关系。
4.2.1 长高比对水平拖曳力系数的影响为了研究长高比对水平拖曳力系数的影响,在已有块体的基础上额外加入4个块体,尺寸分别是4.0 cm×8.0 cm×4.0 cm,5.0 cm×8.0 cm×4.0 cm,6.0 cm×8.0 cm×4.0 cm和16.0 cm×8.0 cm×4.0 cm。保持块体宽高比恒定,长高比对水平拖曳力系数关系曲线如图 8所示。图 9是宽高比为2.0、拖曳力系数处于稳定阶段时块体长高比与水平拖曳力系数关系曲线。
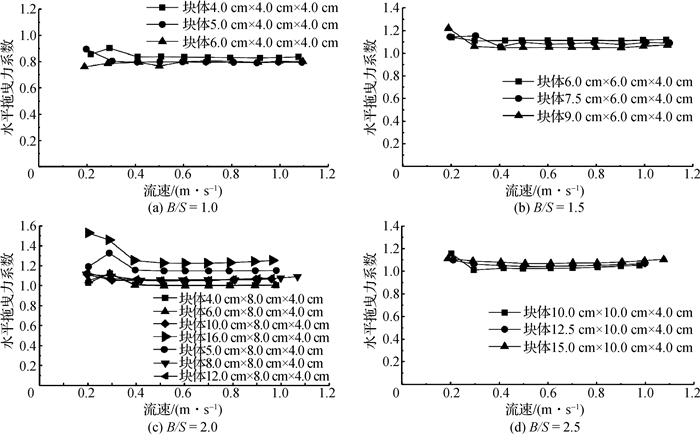
|
图 8 长高比对水平拖曳力系数影响变化 Fig.8 Effects of length-height ratio on horizontal drag force coefficients |

|
图 9 长高比与水平拖曳力系数关系曲线 Fig.9 Effects of length-height ratio on horizontal drag force coefficients |
从图 8可见:(1)流速低于0.4 m/s时,水平拖曳力系数处于不稳定状态;流速大于0.4 m/s时,水平拖曳力系数处于稳定状态。(2)宽高比为1.0时,水平拖曳力系数随长高比增大而减小;宽高比为1.5时,水平拖曳力系数随长高比增大而减小;宽高比为2.0时,水平拖曳力系数随长高比增大而先增后减,然后继续增大;宽高比为2.5时,水平拖曳力系数基本稳定。
图 9更是直观表现了块体长高比对块体水平拖曳力系数的影响:(1)当块体的L/S<2.0时,水平拖曳力系数处于不稳定状态,具有波动性;(2)当2.0≤L/S≤3.0,水平拖曳力系数趋于稳定;(3)当L/S>3.0,水平拖曳力系数随长高比增大而增大。
4.2.2 宽高比对水平拖曳力系数的影响为研究宽高比对水平拖曳力系数的影响,保持块体长宽比恒定,绘制块体不同迎水面宽高比与水平拖曳力系数曲线如图 10和11所示。
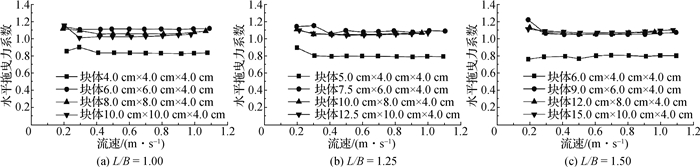
|
图 10 不同宽高比对块体水平拖曳力系数的影响 Fig.10 Effects of different width-height ratios on block horizontal drag force coefficients |

|
图 11 宽高比与水平拖曳力系数关系曲线 Fig.11 Relationship curves between width-height ratio and horizontal drag force coefficients |
由图 10可见:(1)流速低于0.4 m/s时,水平拖曳力系数处于不稳定状态,流速大于0.4 m/s时,水平拖曳力系数处于稳定状态;(2)在块体长宽比恒定的情况下,随着块体宽高比的增大,块体水平拖曳力系数总体趋势增大,最后稳定在CD=1.05。
图 11曲线直观展现了宽高比与水平拖曳力系数之间的关系:(1)当块体B/S≤2.0时,块体水平拖曳力系数随长宽比增大而减小;当B/S>2.0时,长宽比对拖曳力系数影响不大,水平拖曳力系数趋于稳定(约为1.05);(2)当块体B/S < 1.5,水平拖曳力系数随宽高比增大而增大;当1.5≤B/S≤2.0,水平拖曳力系数随宽高比增大而减小;当B/S>2.0,水平拖曳力系数趋于稳定。
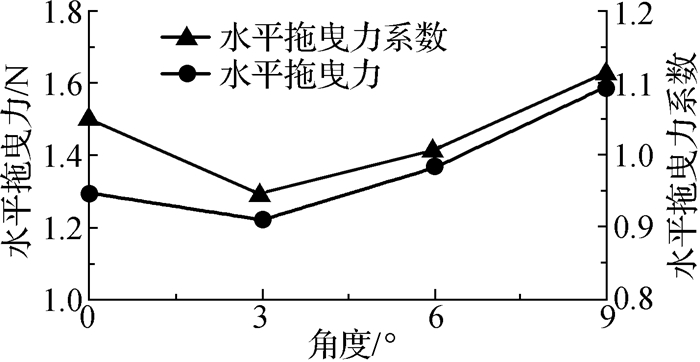
4.3 块体角度变化上述情况都是块体正对着水流,块体长度那一面与水流方向的夹角为0°。为研究不同夹角对块体水平拖曳力系数的影响,将块体5.0 cm×5.0 cm×5.0 cm固定在原点不变,然后逆时针分别旋转3°,6°和9°。图 12表示块体水平拖曳力和水平拖曳力系数在不同夹角情况下与流速的关系曲线,图 13表示在水平拖曳力系数稳定的情况下,块体水平拖曳力和水平拖曳力系数分别与夹角的关系曲线。
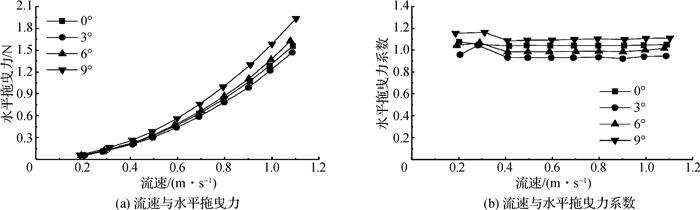
|
图 12 不同块体角度流速与水平拖曳力和拖曳力系数关系曲线 Fig.12 Relationship curves between velocities and horizontal drag force and drag forcecoefficients at different angles |
|
图 13 夹角与水平拖曳力和拖曳力系数关系曲线 Fig.13 Relationship curves between angles and horizontal drag force and drag force coefficients |
由图 12可知:(1)在流速一定的情况下,9°角块体水平拖曳力最大,其次是6°和0°角,3°角块体水平拖曳力最小;(2)当流速低于0.4 m/s时,水平拖曳力系数不稳定,当流速高于0.4 m/s时,水平拖曳力系数趋于稳定;(3)水平拖曳力系数处于稳定状态时,9°角块体水平拖曳力系数最大,其次是0°和6°,3°角块体水平拖曳力系数最小。
图 13中两条曲线的变化趋势一致。夹角小于3°时,块体水平拖曳力和拖曳力系数随角度增大而减小;夹角大于3°时,块体水平拖曳力和拖曳力系数随角度增大而增大。
5 结语基于FLOW-3D软件,对黄河整治工程中垛坝散抛根石水流作用力进行数值模拟。研究表明,块体不同尺寸和摆放角度将会直接影响块体水平拖曳力系数,具体结论如下:
(1) 在同等情况下,块体水平拖曳力系数大于等体积球体的水平拖曳力系数,比值为1.5~2.0。
(2) 当流速小于0.4 m/s时,水平拖曳力系数处于不稳定状态;当流速大于0.4 m/s时,水平拖曳力系数趋于稳定;当块体长高比L/S<2.0,水平拖曳力系数处于不稳定状态,具有波动性;当2.0≤L/S≤3.0,水平拖曳力系数趋于稳定;当L/S>3.0,水平拖曳力系数随长高比增大而增大。当B/S < 1.5,水平拖曳力系数随宽高比增大而增大;当B/S≥1.5,水平拖曳力系数随宽高比增大而减小,最后趋于稳定。
(3) 当块体在水流方向有夹角时,随着夹角增大,块体水平拖曳力系数先减后增,夹角等于3°时,水平拖曳力系数最小。
| [1] |
STEVEN R A, LEECH J R, CHRISTOPHER I T, et al. Articulated concrete block stability testing[J]. Jawra Journal of the American Water Resources Association, 2010, 37(1): 27-34. |
| [2] |
周代鑫, 黄希敏. 截流人工块体稳定性分析[J]. 人民珠江, 1995(1): 18-24. ( ZHOU Daixin, HUANG Ximin. Stability analysis of artificial concrete blocks for closure[J]. Pearl River, 1995(1): 18-24. (in Chinese)) |
| [3] |
杨火其, 王文杰. 强潮河口丁坝坝头块体抗冲稳定分析[J]. 泥沙研究, 2001(5): 14-18. ( YANG Huoqi, WANG Wenjie. Erosion-resisting characteristics of blocks on groin head in micro-tidal river mouths[J]. Journal of Sediment Research, 2001(5): 14-18. DOI:10.3321/j.issn:0468-155X.2001.05.002 (in Chinese)) |
| [4] |
肖焕雄, 唐晓阳. 江河截流中混合粒径群体抛投石料稳定性研究[J]. 水利学报, 1994(3): 10-18. ( XIAO Huanxiong, TANG Xiaoyang. Stability of mixed riprap dumped for river closure[J]. Journal of Hydraulic Engineering, 1994(3): 10-18. DOI:10.3321/j.issn:0559-9350.1994.03.002 (in Chinese)) |
| [5] |
刘大有. 二向流体动力学[M]. 北京: 高等教育出版社, 1993. ( LIU Dayou. Fluid dynamics of two-phase systems[M]. Beijing: Higher Education Press, 1993. (in Chinese))
|
| [6] |
谢鉴衡. 河流泥沙工程学[M]. 北京: 水利电力出版社, 1981. ( XIE Jianheng. River sediment engineering[M]. Beijing: Water Resources and Electric Power Press, 1981. (in Chinese))
|
| [7] |
钱宁, 万兆惠. 泥沙运动力学[M]. 北京: 科学出版社, 2003: 114-122. ( QIAN Ning, WAN Zhaohui. Mechanics of sediment transport[M]. Beijing: Science Press, 2003: 114-122. (in Chinese))
|
| [8] |
PATANIK P C, PANDE P K, VITTAL N. Drag coefficient of a stationary sphere in gradient flow[J]. Journal of Hydraulic Research, 1992, 30(3): 389-402. DOI:10.1080/00221689209498926 |
| [9] |
窦国仁. 再论泥沙起动流速[J]. 泥沙研究, 1999, 12(6): 1-9. ( DOU Guoren. Incipient motion of coarse and fine sediment[J]. Journal of Sediment Research, 1999, 12(6): 1-9. DOI:10.3321/j.issn:0468-155X.1999.06.001 (in Chinese)) |
| [10] |
韩其为, 何明民. 泥沙起动规律及起动流速[M]. 北京: 科学出版社, 1999. ( HAN Qiwei, HE Mingmin. Sediment starting law and starting velocity[M]. Beijing: Science Press, 1999. (in Chinese))
|
| [11] |
缑元有. 河道整治工程根石走失的力学分析研究[J]. 人民黄河, 2000(4): 4-5. ( GOU Yuanyou. Mechanics analysis and study of root rock loss in river channel harness projects[J]. Yellow River, 2000(4): 4-5. DOI:10.3969/j.issn.1000-1379.2000.04.002 (in Chinese)) |
| [12] |
庞启秀.水流作用下块体受力试验研究[D].南京: 河海大学, 2005. (PANG Qixiu. Experimental study of the hydrodynamic forces on the square-section cylinder[D]. Nanjing: Hohai University, 2005. (in Chinese)) http://cdmd.cnki.com.cn/article/cdmd-10294-2005042692.htm
|
| [13] |
庞启秀, 徐金环, 辛海霞. 块体形状对水流拖曳力的影响[J]. 水道港口, 2006, 27(1): 5-8, 22. ( PANG Qixiu, XU Jinhuan, XIN Haixia. Effect of square-section cylinder shape on the drag force[J]. Journal of Waterway and Harbour, 2006, 27(1): 5-8, 22. DOI:10.3969/j.issn.1005-8443.2006.01.002 (in Chinese)) |
| [14] |
陈小莉, 马吉明. 受漩涡作用的水下块石的起动流速[J]. 清华大学学报(自然科学版), 2005, 45(3): 315-318. ( CHEN Xiaoli, MA Jiming. Critical velocity for initiation motion of rocks under water due to vortex motion[J]. Journal of Tsinghua University(Science and Technology), 2005, 45(3): 315-318. DOI:10.3321/j.issn:1000-0054.2005.03.011 (in Chinese)) |
| [15] |
江胜华, 周智, 欧进萍. 桥墩局部冲刷防护的石块起动[J]. 泥沙研究, 2013(4): 63-67. ( JIANG Shenghua, ZHOU Zhi, OU Jinping. Incipient motion of rocks for bridge local scour protection[J]. Journal of Sediment Research, 2013(4): 63-67. DOI:10.3969/j.issn.0468-155X.2013.04.010 (in Chinese)) |
| [16] |
HOERNER S F. Fluid-dynamic drag[M]. Paris: [s. n.], 1965.
|
| [17] |
EVETT J B, LIU C. Fundamentals of fluid mechanics[M]. New York: Me Graw-Hill, 1987: 381-390.
|
| [18] |
MOVAHEDI A, KAVIANPOUR M R, YAMINI O A. Evaluation and modeling scouring and sedimentation around downstream of large dams[J]. Environmental Earth Science, 2018, 77(8): 1-17. |
| [19] |
刘珮勋, 兰雁, 陈宇豪, 等. 坝垛工程根石走失数值模拟[J]. 水利水运工程学报, 2017(5): 45-50. ( LIU Peixun, LAN Yan, CHEN Yuhao, et al. Numerical simulation of root stones lost in dam buttress project[J]. Hydro-Science and Engineering, 2017(5): 45-50. (in Chinese)) |
| [20] |
YAKHOT V, ORSZAG S A. Renormalization-group analysis of turbulence[J]. Physical Review Letters, 1986, 57(14): 1722-1724. DOI:10.1103/PhysRevLett.57.1722 |
| [21] |
HIRT C W, NICHOLS B D. Volume of fluid (VOF) method for the dynamics of free boundaries[J]. Journal of Computational Physics, 1981, 39: 201-225. DOI:10.1016/0021-9991(81)90145-5 |
| [22] |
HIRT C W, SICILIAN J M. A porosity technique for the definition of obstacles in rectangular cell meshes[C]// Proc 4th Int Conf Ship Hydro, National Academy of Science, Washington, 1985.
|
2. Yellow River Institute of Hydraulic Research, Yellow River Water Conservancy Commission, Zhengzhou 450003, China;
3. North China University of Water Resources and Electric Power, Zhengzhou 450045, China;
4. Department of Building Environment and Engineering, The University of Newcastle, Newcastle 2308, Australia
 2019
2019 
