2. 浙江省水利河口研究院 浙江省河口海岸重点实验室,浙江 杭州 310020
涌潮,又称怒潮或暴涨潮,常产生于潮差较大的喇叭形海湾和河口中,是一种水位、流速急剧变化的涨潮潮波前锋线。涌潮蕴藏着巨大的能量,对河道和涉水建筑物等冲击破坏严重[1],国内外学者利用多种手段对涌潮水动力特性进行研究并取得了丰富成果。谢东风等[2]基于实测数据分析了钱塘江涌潮沿程潮位、涨落潮历时等特征,建立了涌潮潮头陡度的计算公式。张巍等[3]利用定点连续观测资料对钱塘江涌潮的潮流特性进行分析。杨火其等[4]通过水槽试验建立了涌潮传播速度与潮前水深、涌潮高度及潮前流速的经验公式。岳书波等[5]利用高速摄像机对比了不同条件下潮头的掺气形态,拟合出潮头掺气长度的计算公式。由于现场观测和物理试验需要大量人力物力,数据质量受采集方式的严重限制,因此数值模拟技术被引入到涌潮研究中并取得了良好效果。根据涌潮数值研究的范围和目的,可将涌潮数学模型分为大尺度和小尺度模型,大尺度模型着眼于研究涌潮形成、发展和衰减整个过程的水力特性,小尺度模型着眼于研究涌潮的阶段性特征。由于本文建立的数学模型为小尺度模型,故只对小尺度模型研究进展做简要综述,大尺度模型的相关介绍可参考谢东风[6]和李大鸣[7]等的研究。Lubin等[8]采用大涡模拟结合水流冲击直立墙的方法研究了涌潮自由表面形态特征。Li等[9]采用SPH法模拟了涌潮通过桥墩的紊动特性。林伟栋等[10]利用溃坝水流法并基于CIP-ZJU模型对回头潮的水面形态特征进行了研究。
然而,前人所建立的数学模型对涌潮生成时上下游边界变化特征的描述不够明确,和真实涌潮生成机制存在明显差异。因此,本文对传统的涌潮生成方法进行改进并基于有限差分法离散控制方程,采用大涡模拟技术模拟紊流,利用VOF法追踪自由表面建立了涌潮水动力数学模型,成功复演了涌潮的生成和传播过程,在验证模型正确性后,对涌潮传播过程中的水力特性及其影响因素展开研究。
1 数学模型 1.1 控制方程基本控制方程为连续性方程和动量方程[11]:
| $ \frac{\partial}{\partial x}\left(u A_{x}\right)+\frac{\partial}{\partial y}\left(v A_{y}\right)+\frac{\partial}{\partial z}\left(w A_{z}\right)=0 $ | (1) |
| $ \left\{\begin{array}{l}{\frac{\partial u}{\partial t}+\frac{1}{V_{f}}\left(u A_{x} \frac{\partial u}{\partial x}+v A_{y} \frac{\partial u}{\partial y}+w A_{z} \frac{\partial u}{\partial z}\right)=-\frac{1}{\rho} \frac{\partial p}{\partial x}+G_{x}+f_{x}} \\ {\frac{\partial v}{\partial t}+\frac{1}{V_{f}}\left(u A_{x} \frac{\partial v}{\partial x}+v A_{y} \frac{\partial v}{\partial y}+w A_{z} \frac{\partial v}{\partial z}\right)=-\frac{1}{\rho} \frac{\partial p}{\partial y}+G_{y}+f_{y}} \\ {\frac{\partial w}{\partial t}+\frac{1}{V_{f}}\left(u A_{x} \frac{\partial w}{\partial x}+v A_{y} \frac{\partial w}{\partial y}+w A_{z} \frac{\partial w}{\partial z}\right)=-\frac{1}{\rho} \frac{\partial p}{\partial z}+G_{z}+f_{z}}\end{array}\right. $ | (2) |
式中:u,v,w分别对应x,y,z的速度分量;Ax,Ay,Az分别为x,y,z方向上可流动的面积百分比;Vf为可流动的体积百分比;Gx,Gy,Gz分别为x,y,z方向的重力加速度;ρ为流体密度;p为压强;fx,fy,fz分别为x,y,z方向上的黏滞力。
1.2 紊流模型及VOF简介由于模拟的目标是再现自由水面波动和流场结构变化特征,主要困难在于准确再现涌潮过程中瞬态自由面演化和非定常流动引起的湍流问题,因此选择广泛应用于流体流动细节模拟的大涡模拟技术(LES)模拟湍流。大涡模拟技术的主要原理是放弃用完全精确的控制方程对紊流进行数值模拟,将流体中的涡旋结构划分为大尺度涡旋与小尺度涡旋,通过滤波方式把小尺度涡结构滤出[12]。对于大尺度涡结构采用N-S方程进行直接数值模拟,小尺度涡结构相对于大结构涡的影响在运动方程中表现为类似于雷诺应力一样的附加项,称为亚格子应力,采用雷诺平均理论计算。VOF法[13]通过对自由液面的追踪从而求解一套动量方程和连续性方程来模拟两种或多种互不掺混的流体流动,适合于分层流动或带有自由表面流动的相关问题研究,LES模型和VOF法的更多内容请参见陈琼等[14]的介绍。
1.3 计算区域及边界条件涌潮生成过程如图 1所示,图中V0为落潮流速;h0为潮前水深;c为涌潮传播速度;H为涌潮高度;h1和V1分别为涌潮生成时的水位和流速。涌潮尚未生成时,水体向下游流动,上下游水位和流速皆为h0和V0;涌潮生成时,上游边界条件保持不变,下游边界处水位突然升高,流速方向改变并增大,随后水体向上游传播。目前国内外学者对涌潮进行小尺度数值模拟时,选用的涌潮生成方式均难以符合实际,例如采用溃坝方式产生的涌潮在隔离板抽取时壅高部分的水体横向流速(V1)几乎为零,采用推波板造波方式产生的涌潮上下游流速(V0和V1)呈同向变化,这都与实际不符;采用水流冲击直立墙产生涌潮的方式则无法有效控制所产生的涌潮初始水位和流速(h1和V1),使得所产生的涌潮过程具有明显的随机性。很显然,要想成功实现涌潮小尺度数值模拟的关键在于恰当地给定h1和V1。倪兴也等[15]基于SPH开边界技术将边界流量拆解为水位和流速分别进行控制,实现了对涌潮的数值模拟并利用2010年盐官河段现场测量资料验证了此种边界赋予方法的有效性,虽然也是通过不断调整涨潮流速才使其传播速度与实测传播速度相一致。
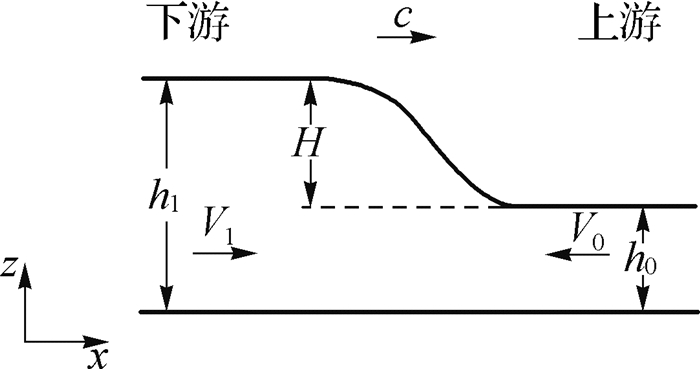
|
图 1 涌潮生成初始条件 Fig.1 Initial conditions for tidal bore generation |
潘存鸿等[16]基于一维连续性方程和动量方程推导出涌潮传播流速公式:
| $ c=V_{0}+\sqrt{\frac{g h_{1}\left(h_{1}+h_{0}\right)}{2 h_{0}}} $ | (3) |
| $ c=V_{1}+\sqrt{\frac{g h_{0}\left(h_{1}+h_{0}\right)}{2 h_{1}}} $ | (4) |
从上述公式中可以看出,在理想流体条件下,当边界条件中的V0,H,h0条件已知时,可通过联立式(3)和(4)求解出潮涌生成时h1和V1的值,由此控制边界条件,从而对涌潮产生过程进行复演。
基于上述边界条件赋予方法建立了计算域尺寸x>10c,y>2h1,z>2h1的数值模型,压力速度分离式解法采用极小残差算法(GMRES),并基于有限差分法离散控制方程,对涌潮传播过程中速度波动规律及形态影响因素进行了研究。
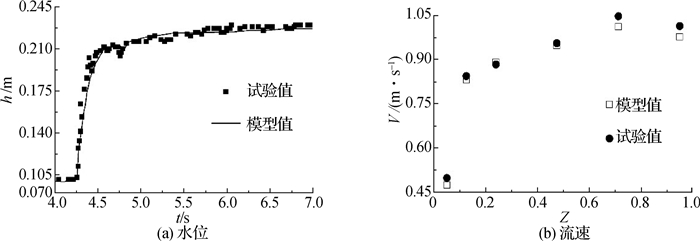
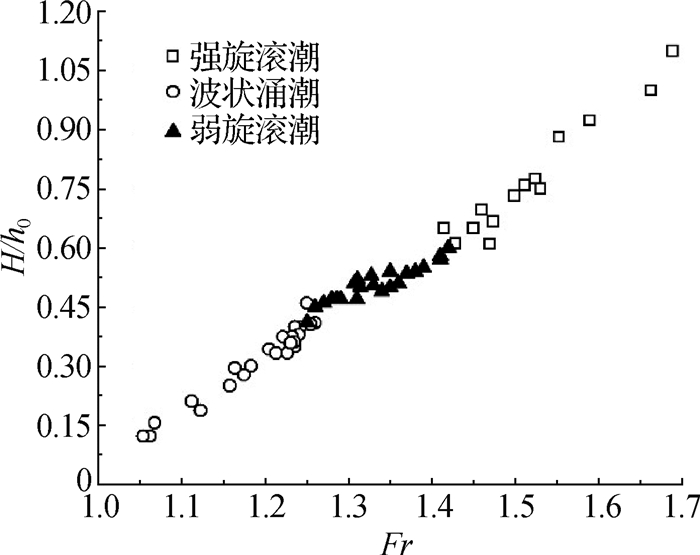
2 涌潮水力特性分析 2.1 模型验证为检验所建数学模型的正确性,使用模型计算值分别与理论公式值和模型试验值进行对比,并将涌潮形态的模拟结果和弗劳德数(Fr)形态判别法进行对比。由于篇幅有限,仅在表中列出部分主要研究工况进行比较,结果如表 1和图 2,3所示。图 2中V为合速度,Z为无量纲水深,Z=d/h0,d为测点距水槽底部的垂向距离,h0为潮前水深。
| 表 1 数值模拟计算工况 Tab.1 Working conditions given by numerical simulation calculation |
|
图 2 模型试验和数值模拟水位、流速比较 Fig.2 Comparison between measured and simulated values of water level and velocity |
|
图 3 Fr与H/h0关系 Fig.3 Relationship curves between Fr and H/h0 |
从表 1的分析结果可知,所建立的涌潮数学模型关于涌潮水动力特性的计算结果与理论值之间最大相对误差不超过10%,出现计算值比理论值偏小的原因可能是由于理论公式推导过程中假定流体为理想流体,而采用的紊流模型并未忽略流体黏性的影响,因此产生一定的误差。同时还将h0=0.1 m,V0=0,H=0.11 m(V0为落潮流速, H为涌潮高度)条件下涌潮数值模拟计算结果与岳书波[17]所做矩形涌潮水槽试验结果进行对比(见图 2),在相对水深较大即表层水体部分,物理试验值比数值模拟计算值偏大的原因可能是由于表层水体部分存在掺气现象,由于测量设备的限制和数值模拟中对水-气两相互相掺混流问题的求解存在不足而引起误差。
综上可见,借鉴波浪边界造波方法,通过在边界上赋予理论公式推导出的流速和水深来模拟涌潮是可行的。但需要指出的是,以上理论公式假定了河道地形及岸线不变,实际情况中不同位置的河道地形及岸线不尽相同,其传播速度及流速分布会有所差异。针对不同位置涌潮模拟,需根据实测涌潮资料对传播速度公式进行修正,进而反求出合理的涨潮流速,才能保证模拟涌潮与实际涌潮无限接近。
目前国内外学者关于涌潮形态方面的判据,使用较广的是Koch等[18]基于水槽试验总结的Fr判别法:
| $ F r=\frac{c+V_{0}}{\sqrt{g h_{0}}} $ | (5) |
当1.2 < Fr < 1.3时,水体表面开始波动形成波状阵列,称为波状涌潮;当1.3 < Fr < 1.5时,潮头轻微破碎,称为弱旋滚潮;当Fr>1.5时,潮头完全破碎,称为强旋滚潮。
模拟所得的涌潮形态在Fr>1.44时,涌潮潮头完全破碎,为强旋滚潮;当1.26 < Fr < 1.44时,涌潮潮头轻微或局部破碎;当Fr < 1.26时,涌潮潮头为波状阵列,这与Koch等的结果基本一致。因此,可认为所建涌潮水动力模型有效可行。
2.2 二、三维模拟结果对比涌潮在传播过程中潮头部分不断伴随着能量转换,势必会对整个涌潮过程产生影响。由于二维与三维模拟结果基本相同,在平面曲线图中显示为重合曲线,故仅针对波状涌潮分别选取x,z坐标相同,y=0.25,0.50,0.75 m的3个点进行分析。将特征点处水位和纵向流速随时间变化绘制如图 4所示。从图 4可见,3个特征点处水位和流速保持同步变化,说明波状涌潮在传播过程中不同横断面处的水体间干扰很小,传播过程中其自由水面形态和流速分布情况基本相同。二维数值模型仅需少量计算资源就能满足精度要求,因此,后续分析中均采用二维数值模拟结果。

|
图 4 波状涌潮三维特性 Fig.4 Three-dimensional characteristics of undular tidal bore |
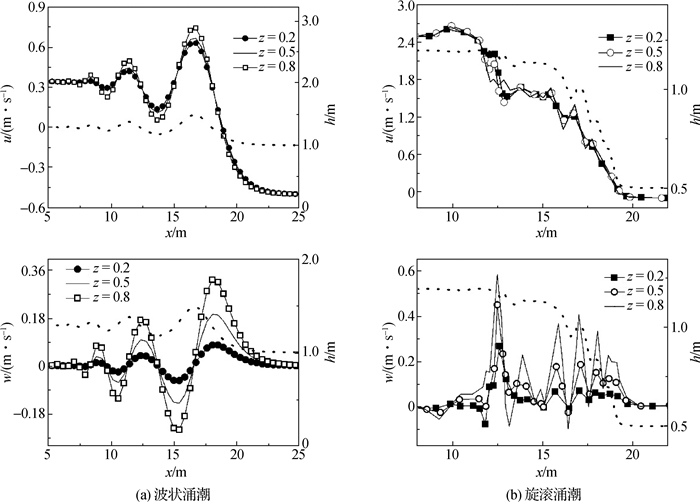
涌潮存在两种典型形态:一种是强度较小时,涌潮由一系列平行向前推进的波构成的波列,称为波状涌潮;另一种是强度较大时,自由表面破碎,形成向前推进的旋滚,称为旋滚涌潮。定义纵向的正方向为涌潮传播方向(从下游指向上游),竖直向上从底部指向自由水面方向为垂向的正方向。分别取同一时刻下不同无量纲水深处流速分布绘制如图 5所示,图中黑色虚线代表自由水面形态,u,w分别代表纵向和垂向流速。
|
图 5 涌潮流速分布对比 Fig.5 Comparison between velocity distributions of tidal bore |
从图 5可以看出,两种涌潮传播过程中各方向上的流速波动在整体上都呈现出随自由水面波动而相应震荡的特点。表层水体各向流速波动皆大于中底层水体,但就纵向速度而言,各层水体流速比较接近。波状涌潮在传播过程中,两个方向上流速波动最大值皆出现在最前方潮头附近。随着潮头不断向前传播,各向流速波动皆呈现出周期性变化,即涨潮段增加落潮段衰减。在同一涨潮周期内,波状涌潮的涨、落潮阶段垂向水体的运动方向相反。此外,通过对比流速最大值和潮头最高点出现位置,可以发现波状涌潮纵向流速变化与自由水面波动基本同步,垂向流速波动最大位置稍提前于自由水面波动最大位置。
旋滚涌潮的流速分布不如波状涌潮有规律性,在传播过程中呈现出较强的紊动特性。从图 5可以明显看出各方向流速波动最大位置皆位于潮头旋滚处。旋滚涌潮纵向流速在潮头破碎处明显减小,其原因是由于涨落潮交汇处水流要素急剧变化,涌潮部分能量转化为热能从而不断损失,导致涌潮高度和传播速度衰减。而垂向流速在潮头破碎处波动剧烈,可能是由于潮头破碎时表层水体内有大量空气卷入,掺入的气体以气泡形式在水体内部向前和向上运动并在此过程中伴随着变形和破裂现象产生,从而造成水体内部流速波动。此外,涨、落潮交汇处水体间发生相互碰撞形成水舌,部分水舌被卷入潮头内部从而造成潮头部分水体强烈紊动继而引发流速波动。
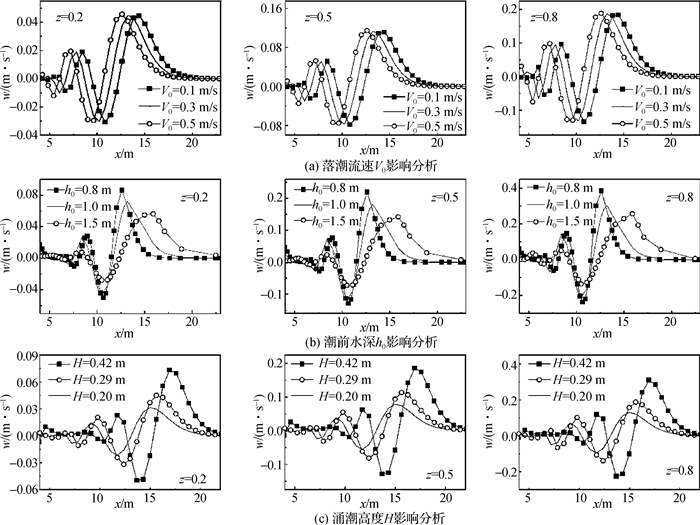
3 波状涌潮影响因素分析涌潮是一种下游水位和流速突然变化的强非线性间断流水力现象,其水力特性受落潮流速、潮前水深、涌潮高度、河床地形、河道形态等因素影响。因本文所建涌潮模拟方法主要用于未来涉水建筑物涌潮水动力特征研究,只需保证建筑物前沿涌潮参数与实际一致即可,无需考虑河道地形及岸线影响。对于某一特定河道或物理模型试验而言,河道形态(或水槽形式)和河床地形(或槽底糙率)是固定的。此外,由于旋滚涌潮的自由水面形态及其流速分布具有较强紊动特性,目前作者尚未找到合适的定量对比研究方法,因此,通过建立矩形直立式数值水槽,分别以落潮流速V0、潮前水深h0和相对涌潮高度H/h0为控制变量对波状涌潮流速波动及形态变化的影响展开研究。
3.1 流速波动特征影响因素分析从图 5可以看出,波状涌潮传播过程中纵向流速可以通过垂向流速波动峰值所在位置进行大致比较,所以对涌潮传播过程中的垂向流速分布进行分析就可以反映出其余两个方向的流速特征。单因素影响下的各工况模拟结果见图 6。从整体上来说,在单因素影响下,波状涌潮的表中层水体流速波动基本保持相同规律,垂向流速自水面向底部逐渐衰减。图 6(a)中3种工况下的表中层水体垂向流速波动幅度没有明显差异,但是V0=0.1 m/s时所生成的涌潮其纵向流速稍大于其余两种工况,因此可认为在其他条件一定时,V0对垂向流速波动基本无影响,但与纵向流速的大小成反比。从图 6(b)和(c)中可以看出,不同h0和H下生成涌潮的垂向流速的波动情况存在明显差异,h0=1.5 m和H=0.42 m对应工况下涌潮垂向流速波动位置明显靠前,可认为在其他条件相同时,h0和H与对应生成涌潮的纵向流速大小成正比。此外还可发现h0=0.8 m和H=0.42 m生成的涌潮垂向流速明显大于其余两种工况。因此还可以认为h0与涌潮的垂向流速波动成反比,H与涌潮的垂向流速波动成正比。总体而言,若仅考虑单一变量的影响,h0和H比V0对涌潮传播过程中的流速波动现象的影响程度更大。
|
图 6 流速影响因素分析 Fig.6 Analysis of influencing factors of flow velocities |
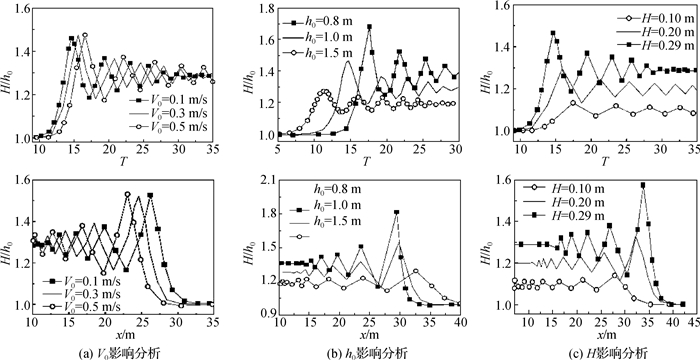
为了更好地对比涌潮形态随时间的演化特征,定义无量纲时间
|
图 7 涌潮形态对比 Fig.7 Comparison of tidal bore patterns |
从图 7可见,波状涌潮的最大波幅和陡度均出现在第1个波峰位置,随后在传播过程中急剧衰减。通过对比水位及流速波动位置可以发现在涌潮过程中水力要素存在明显的波动不等时性。从图 7(a)可以看出V0=0.1 m/s时生成的涌潮,其水体恢复平整所需时间最短,3种V0条件下生成的涌潮,其相对涌潮高度(波幅)基本相同。产生这种情况是因为V0越大时,涌潮传播过程中前方水体对潮头产生的作用越明显,两种不同流态水体间产生的水力间断现象越严重,从而导致水体波动范围越大,其自由水面恢复平整所需时间更长。从图 7(b)中可以看出随着h0的增大,生成的涌潮波幅变小。涌潮在传播过程中,不同涨、落潮周期之间相对涌潮高度的衰减幅度相应变小,但是涌潮传播经过某一特征点后,该点处的自由水面波动持续时间也相应减小,在相对较短的时间内恢复平整。从图 7(c)中可以看出H=0.29 m时生成的涌潮潮头在通过固定点后,自由水面只需更短的时间即能恢复平整。并且,随着H的增加,涌潮的波幅也相应增大,相邻涨、落潮周期内相对涌潮高度的衰减幅度比其余工况更大。出现这种现象可能是由于涌潮传播过程中上下游边界条件并未发生变化,整体水深较大的涌潮所具备的能量越多,在潮头向前传播过程中除去前端潮头消耗部分动能后,剩余能维持自由水面形态的势能越大,从而导致后续水体间产生水力间断现象较弱。就单一影响因素而言,h0和H比V0对涌潮传播过程中形态变化的影响更明显。
4 结语采用改进的边界赋予方法结合LES紊流模型建立涌潮水动力数学模型,可以很好地实现对涌潮传播过程中流速和自由水面变化的动态捕捉。通过对涌潮传播过程中流速和形态影响因素展开研究,经过比较分析可以得出以下结论:
(1) 无论是波状涌潮还是旋滚涌潮,流速最大位置都位于潮头处,且涌潮传播过程中表层流速波动大于中低层流速波动。
(2) 旋滚涌潮潮头水体紊动特性比波状涌潮强烈,涌潮传播过程中,垂向流速波动提前于纵向流速波动。
(3) 涌潮传播过程中h0和H对潮头流速波动和形态变化起主导作用,其他条件相同时,落潮流速V0越大,自由水面波动持续时间越长。V0对涌潮垂向流速波动基本无影响,与纵向流速大小呈反比;h0越大时,涌潮具有的波幅越小,自由水面越容易恢复平整,h0与涌潮垂向流速波动范围呈反比,与纵向流速呈正比;H越大,涌潮具有的波幅越大,自由水面越容易恢复平整,H与涌潮垂向流速波动范围呈正比,与纵向流速呈正比。
| [1] |
刘文虎, 朱小华, 张钟哲, 等. 钱塘江涌潮观测及其动力学特性研究[J]. 大连海洋大学学报, 2015, 30(5): 567-572. ( LIU Wenhu, ZHU Xiaohua, ZHANG Zhongzhe, et al. Observation and dynamic characteristics of tidal bore in Qiantang River, China[J]. Journal of Dalian Ocean University, 2015, 30(5): 567-572. (in Chinese)) |
| [2] |
谢东风, 潘存鸿, 陆波, 等. 基于实测资料的钱塘江涌潮水动力学特性研究[J]. 水动力学研究与进展(A辑), 2012, 27(5): 501-508. ( XIE Dongfeng, PAN Cunhong, LU Bo, et al. A study of the hydrodynamic characteristics of the Qiantang tidal bore based on field data[J]. Chinese Journal of Hydrodynamics, 2012, 27(5): 501-508. (in Chinese)) |
| [3] |
张巍, 贺治国, 谈利明, 等. 基于定点连续观测的钱塘江涌潮特性研究[J]. 水动力学研究与进展(A辑), 2017, 32(2): 253-259. ( ZHANG Wei, HE Zhiguo, TAN Liming, et al. Dynamic characteristics of Qiantang tidal bore based on field observations at a fixed location[J]. Chinese Journal of Hydrodynamics, 2017, 32(2): 253-259. (in Chinese)) |
| [4] |
杨火其, 潘存鸿, 周建炯, 等. 涌潮水力学特性试验研究[J]. 水电能源科学, 2008, 26(4): 136-138. ( YANG Huoqi, PAN Cunhong, ZHOU Jianjiong, et al. Experiment study on hydraulic properties of tidal bore[J]. Water Resources and Power, 2008, 26(4): 136-138. DOI:10.3969/j.issn.1000-7709.2008.04.042 (in Chinese)) |
| [5] |
岳书波, 曾剑, 陈永平, 等. 涌潮潮头掺气的模型试验研究[J]. 工程科学与技术, 2018, 50(1): 28-35. ( YUE Shubo, ZENG Jian, CHEN Yongping, et al. Investigation of aeration of tidal bore front by physical experiments[J]. Advanced Engineering Sciences, 2018, 50(1): 28-35. (in Chinese)) |
| [6] |
谢东风, 潘存鸿, 鲁海燕, 等. 钱塘江河口涌潮传播速度研究[J]. 浙江大学学报(工学版), 2012, 46(6): 1128-1134. ( XIE Dongfeng, PAN Cunhong, LU Haiyan, et al. Study on propagation speed of tidal bore on Qiantang River[J]. Journal of Zhejiang University(Natural Science Edition), 2012, 46(6): 1128-1134. DOI:10.3785/j.issn.1008-973X.2012.06.025 (in Chinese)) |
| [7] |
李大鸣, 张弘强, 卜世龙, 等. 潮流发电试验场水动力特性数学模型研究[J]. 水力发电学报, 2017, 36(12): 105-120. ( LI Daming, ZHANG Hongqiang, BU Shilong, et al. Mathematical modeling of hydrodynamic characteristics of tidal power generation test field[J]. Journal of Hydroelectric Engineering, 2017, 36(12): 105-120. DOI:10.11660/slfdxb.20171212 (in Chinese)) |
| [8] |
LUBIN P, GLOCKNER S, CHANSON H. Numerical simulation of a weak breaking tidal bore[J]. Mechanics Research Communications, 2010, 37(1): 119-121. DOI:10.1016/j.mechrescom.2009.09.008 |
| [9] |
LI Jing, LIU Huaxing, TAN S K. Lagrangian modeling of tidal bores passing through bridge piers[J]. Journal of Hydrodynamics (Ser B), 2010, 22(5): 513-519. |
| [10] |
林伟栋, 赵西增, 叶洲腾, 等. 涌潮运动的CFD模拟研究[J]. 水动力学研究与进展(A辑), 2017, 32(6): 696-703. ( LIN Weidong, ZHAO Xizeng, YE Zhouteng, et al. Numerical simulation of tidal bore using CFD model[J]. Chinese Journal of Hydrodynamics, 2017, 32(6): 696-703. (in Chinese)) |
| [11] |
戚蓝, 陈辉, 费文才, 等. 基于精确河道地形的溢流坝泄流三维数值模拟[J]. 水力发电学报, 2016, 35(10): 12-20. ( QI Lan, CHEN Hui, FEI Wencai, et al. Three-dimensional numerical simulations of flows over spillway dam using accurate river terrain[J]. Journal of Hydroelectric Engineering, 2016, 35(10): 12-20. DOI:10.11660/slfdxb.20161002 (in Chinese)) |
| [12] |
薛万云, 郭宁, 吴时强, 等. 桥墩水流特性大涡模拟研究[J]. 水利水运工程学报, 2016(4): 18-26. ( XUE Wanyun, GUO Ning, WU Shiqiang, et al. Impacts of multiple bridge piers upon open channel flow based on LES[J]. Hydro-Science and Engineering, 2016(4): 18-26. (in Chinese)) |
| [13] |
ZHANG Zhiyong, SHI Bin, GUO Yakun, et al. Numerical investigation on critical length of impermeable plate below underwater pipeline under steady current[J]. Science China Technological Sciences, 2013, 56(5): 1232-1240. DOI:10.1007/s11431-013-5194-5 |
| [14] |
陈琼, 李云, 刘本芹, 等. 高水头船闸一字闸门水动力特性数值模拟[J]. 水利水运工程学报, 2017(1): 87-94. ( CHEN Qiong, LI Yun, LIU Benqin, et al. Numerical simulation of hydrodynamic characteristics of single-leaf gate of high-head navigation lock[J]. Hydro-Science and Engineering, 2017(1): 87-94. (in Chinese)) |
| [15] |
倪兴也, 黄世昌, 冯卫兵, 等.基于SPH方法的涌潮数值模拟研究[C]//第十八届中国海洋(岸)工程学术讨论会, 2017: 289-299. (NI Xinye, HUANG Shichang, FENG Weibin, et al. Numerical simulation of tidal current based on SPH method[C]//The 18th China Ocean (Coastal) Engineering Symposium, 2017: 289-299. (in Chinese))
|
| [16] |
潘存鸿, 鲁海燕, 曾剑. 钱塘江涌潮特性及其数值模拟[J]. 水利水运工程学报, 2008(2): 1-9. ( PAN Cunhong, LU Haiyan, ZENG Jian. Characteristic and numerical simulation of tidal bore in Qiantang River[J]. Hydro-Science and Engineering, 2008(2): 1-9. DOI:10.3969/j.issn.1009-640X.2008.02.001 (in Chinese)) |
| [17] |
岳书波.强涌潮潮头紊流特性的模型试验研究[R].杭州: 浙江省水利河口研究院, 2017. (YUE Shubo. Experimental study on turbulent characteristics of tidal bore front[R]. Hangzhou: Zhejiang Institute of Hydraulics and Estuary, 2017. (in Chinese))
|
| [18] |
KOCH C, CHANSON H. An experimental study of tidal bores and positive surges: Hydrodynamics and turbulence of the bore front[R]. Brisbane: University of Queenland, 2005.
|
2. Key Lab of Estuary and Coast of Zhejiang Province, Zhejiang Institute of Hydraulics and Estuary, Hangzhou 310020, China
 2019
2019 