航道整治工程实施后,受各种因素影响丁坝在服役过程中的技术状况随时间发生变化,并且随着河床演变,丁坝的功能也可能发生变化。目前国内外关于丁坝群的研究,多着眼于坝头局部冲刷、丁坝附近流场数值模拟、丁坝寿命预测等[1-3],对于整治建筑物功能预测较少。
丁坝群束水攻沙功能是复杂的非线性问题,数学模型和物理模型难以满足日常维护管理的需求[4]。基于支持向量机的预测模型具有解决有限样本、非线性及高维识别问题的优势,在水科学方面就有关于水流边坡稳定性、水流挟沙力等的预测[5],本文探讨支持向量机(Support Vector Machine,SVM)在丁坝群束水攻沙功能预测中的应用。
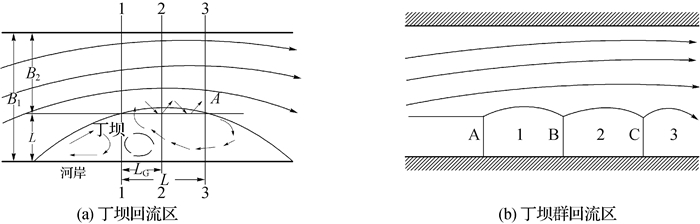
1 丁坝群束水攻沙功能的评价指标 1.1 丁坝群束水攻沙功能形成机理丁坝坝顶露出水面处于非淹没状态时,水流流向丁坝受丁坝壅阻,水面比降降低,水流流速减缓,接近丁坝时出现反比降,丁坝断面水流收缩。在惯性力的作用下,水流绕过丁坝后进一步收缩,在距丁坝下游LG处,形成一个收缩断面(见图 1(a)2-2断面),在该断面处水流的动能最大且断面平均流速最大。在收缩断面下游,水流逐渐扩散,动能减小而位能增大,至A点处,水流的压缩程度与丁坝断面相当,称A点断面为扩散断面(3-3断面)。在扩散断面下游,水流继续扩大,至丁坝掩护末端,水流恢复至天然状态。在丁坝坝头外主流与丁坝掩护区缓流强大摩擦梯度作用下,一般情况下丁坝上下游常形成图 1(a)所示的几个回流区,在这些回流区内流速滞缓,泥沙容易落淤。在丁坝影响下流速增大区域,河槽浅滩被冲深,泥沙下移或随丁坝下游的回流导入两坝之间的坝田。
|
图 1 丁坝及丁坝群回流区 Fig.1 Schematic diagram of a spur dike's and spur dikes' recirculation areas |
丁坝群形成的水流现象如图 1(b)所示,常福田等[6]采用物理模型试验研究丁坝群坝距对水流的影响,得出了以下结论:丁坝群间距继续减小到某一间距范围时,坝后回流区与主流的分界线几乎沿着坝头与河岸平行,主流稳定。韩玉芳[7]研究发现:在丁坝群的作用下,如果丁坝间距合适,往往在丁坝头部连线处形成连贯的冲刷槽,冲刷槽的形成比河床的普遍调整要迅速得多;丁坝群引起的河床调整过程中流场的变化过程与单丁坝是一致的,断面流速分布发生了较大变化,靠近河岸回流区的流速明显小于之前无丁坝群作用时,而河道中心水流流速增大,在形成稳定流场后略有下降,但仍然较之前无丁坝群作用时有明显提升。
在图 1(b)丁坝A,B,C形成的丁坝群中,丁坝后方水域1~3形成了坝后回流区,主流被约束变窄并保持稳定,主流流速较无丁坝群作用时增加。丁坝群可以稳定主流,约束水流,设计最低通航水位时的河面宽度减小,断面平均流速增加,水流输沙能力增强,浅滩冲刷,航道水深增加;丁坝群的束水攻沙功能得以实现。
1.2 丁坝群束水攻沙功能指标功能指标筛选原则:(1)功能指标能正确反映丁坝在航道演变中发挥的作用。功能指标既要能反映整治工程设计目标,又要能反映航道演变的状况。(2)功能指标要有可操作性,便于采集。这要求功能指标基于目前的监测手段能够经济合理地获取,或根据已测量的数据,通过模型计算获取。(3)功能指标要以定量为主,便于客观分析,便于与信息化集成。
从丁坝群束水攻沙功能的形成机理不难发现,反映束水攻沙功能的指标有设计最低通航水位时的河面宽度、断面平均水深、主流的摆幅、断面平均流速等。
设计最低通航水位时的河面宽度较好地反映了河床束窄的效果,可以用0 m线最小宽度来反映。0 m线宽度是航道两侧滩缘最低通航水位时的河面宽,0 m线最小宽度近年呈减小趋势,说明束水功能发挥作用。河道断面形态的变化反映了束水攻沙作用的综合效果。宽深比常用来反映断面形态的演变,因此,可选择宽深比作为束水攻沙功能的指标。计算宽深比时选择的断面为丁坝群作用水域水面最宽的位置,宽深比越小说明冲深效果越佳。断面平均流速不易测量,从实用性的角度可以排除;从文献[6]的研究看,丁坝群所在区域主流稳定,主流的摆幅暂不列为功能指标。因此,本文丁坝群束水攻沙功能指标为设计最低通航水位时的河面宽度以及宽深比。
2 基于支持向量机理论的预测模型 2.1 回归支持向量机自20世纪90年代以来,有限样本下的机器学习理论得以大范围研究,由此产生了一种新的机器学习方法——支持向量机(Support Vector Machine, SVM)[8-9]。该方法是在结构风险最小的原理基础上, 用来替代传统统计学中的经验风险最小化[10-12]。支持向量机方法能够根据有限的样本信息在模型的复杂性和学习能力之间寻求最优解,以期获得最好的应用能力[13]。
回归支持向量机是本次研究采用的模型,算法如下:给定l个样本数据{xk, yk}l,其中xk∈Rn是n维样本输入,yk∈R为样本输出,则函数回归问题的实质就是要找出一个函数f,使之通过样本训练后,样本中的x通过f能与样本中y对应起来,进而对于样本以外的x,可以通过f找出对应的y。在处理非线性问题时引入核函数方法,使输入样本空间的非线性变换到一个高维的线性特征空间,并在此空间中利用线性方法解决非线性问题。设函数具有如下的形式:
| $ f(x)=\omega^{\mathrm{T}} \varphi\left(x_{k}\right)+b, \omega \in R^{n h}, b \in R $ | (1) |
式中:ω为惯性权重; 非线性函数
| $ |y - f(x){|_\varepsilon } = \max \{ 0, |y - f(x)| - \varepsilon \} $ |
需要寻找最优ω,b,根据结构风险最小化原理,得到的最优化问题为:
| $ \begin{array}{l} \mathop {\min }\limits_{\omega , b, \vartheta , {\vartheta ^*}} J = \frac{1}{2}{\omega ^{\rm{T}}}\omega \\ {\rm{s}}{\rm{.t}}{\rm{.}}\left\{ {\begin{array}{*{20}{l}} {{y_i} - {\omega ^{\rm{T}}}\varphi \left( {{x_i}} \right) - b \le \varepsilon }\\ {{\omega ^{\rm{T}}}\varphi \left( {{x_i}} \right) + b - {y_i} \le \varepsilon } \end{array}\quad i = 1, 2, \cdots , l} \right. \end{array} $ | (2) |
当约束条件无法实现时,通过引入松弛变量ϑi,θi*将最优化问题转化为如下形式:
| $ \begin{array}{l} \mathop {\min }\limits_{\omega , b, \vartheta , {\vartheta ^*}} J = \frac{1}{2}{\omega ^{\rm{T}}}\omega + C\sum\limits_{i = 1}^l {\left( {{\vartheta _i} + \theta _i^*} \right)} \\ {\rm{s}}{\rm{.t}}{\rm{.}}\left\{ {\begin{array}{*{20}{l}} {{y_i} - {\omega ^{\rm{T}}}\varphi \left( {{x_i}} \right) - b \le \varepsilon + {\vartheta _i}}\\ \begin{array}{l} {\omega ^{\rm{T}}}\varphi \left( {{x_i}} \right) + b - {y_i} \le \varepsilon + \theta _i^*\\ \;\;\;\;\;\;\;\;\;\;{\vartheta _i}, \theta _i^* \ge 0 \end{array} \end{array}\quad i = 1, 2, \cdots , l} \right. \end{array} $ | (3) |
式中:ε为回归允许最大误差;C为惩罚常数, 表示函数f的复杂度和样本拟合精度之间的折中。C>0,其值越大对训练误差大于ε的样本惩罚越大;C值趋于零时,模型失去解决问题的能力。
利用拉格朗日乘子法求解凸二次型规划问题,所得结果如下:
| $ \begin{array}{l} \mathop {\min }\limits_{\alpha , {\alpha ^*}} \frac{1}{2}\sum\limits_{i, j = 1}^l {\left( {{\alpha _i} - \alpha _i^*} \right)} \left( {{\alpha _j} - \alpha _j^*} \right)k\left( {{x_i}, {y_i}} \right) + \varepsilon \sum\limits_{i = 1}^l {\left( {{\alpha _i} + \alpha _i^*} \right)} - \sum\limits_{i = 1}^l {{y_i}} \left( {{\alpha _i} - \alpha _i^*} \right)\\ {\rm{s}}{\rm{.t}}{\rm{.}}\left\{ {\begin{array}{*{20}{c}} {\sum\limits_{i = 1}^l {\left( {{\alpha _i} - \alpha _i^*} \right)} = 0}\\ {{\alpha _i}, \alpha _i^* \in [c, C]} \end{array}} \right. \end{array} $ | (4) |
从而通过学习得到的回归估计函数为:
| $ \omega=\sum\limits_{i=1}^{l}\left(\alpha_{i}-\alpha_{i}^{*}\right) \varphi\left(x_{i}\right) ; f(x)=\sum\limits_{i=1}^{l}\left(\alpha_{i}-\alpha_{i}^{*}\right) k\left(x_{i}, x\right) $ | (5) |
核函数
| $ \begin{array}{l} b = {y_i} - \sum\limits_{i = 1}^l {\left( {{\alpha _i} - \alpha _i^*} \right)} k\left( {{x_i}, x} \right) - \varepsilon , {\alpha _i} \in (0, C)\;\;\;或\\ b = {y_i} - \sum\limits_{i = 1}^l {\left( {{\alpha _i} - \alpha _i^*} \right)} k\left( {{x_i}, x} \right) + \varepsilon , \alpha _i^* \in (0, C) \end{array} $ | (6) |
利用上述KKT条件可以求得参数b,这样便可以求出估计函数f(x)[14]。
2.2 基于回归向量基的预测模型构建 2.2.1 核函数及相关参数选择在构造回归支持向量机模型过程中, 核函数类型的选择是重中之重。SVM中常用的核函数类型有以下4种:线性核函数、多项式核函数、RBF核函数、sigmoid核函数。4种核函数的选择要结合具体的训练样本, 确定一个比较合适的综合解决方案。关于核函数选择的理论仍然很少, 目前大多采用试算法选出更适合的核函数。
核函数类型确定后,再确定相关参数的选择。上述算法中的参数主要有不灵敏参数ε、惩罚常数C和核函数参数σ,通过交叉验证试算找出合适的参数值。
2.2.2 训练样本的输入、输出因子选择丁坝群束水攻沙功能指标的影响因素主要有5个方面:
(1) 河段上游来水量及其变化过程, 是河床冲淤变化的主要影响因素,选择各时段的总径流量Q来反映该时段的来水量,选择各时段内流量小于15 000,20 000,30 000,40 000及40 000 m3/s以上的天数来反映该时段的来水过程。统计逐日平均流量变化天数的流量分类标准需根据研究河段水文情况来调整。
(2) 河段上游来沙量、来沙组成及其变化过程。选择各时段的总输沙量G、年平均中值粒径D50为输入因子,来反映该时段的来沙量。选择各时段内含沙量小于85,120,170,200及200 g/m3以上的天数来反映该时段的来沙过程。统计逐日平均含沙量变化天数的分类标准依照具体河段情况来调整。
(3) 河段的水面比降。目标河段上、下游水位的变化反映了该河段水面比降的变化, 因此下游水位(ZD)可作为输入因子。
(4) 河段的河床形态及床沙组成。河床形态采用(
(5) 人类活动影响。研究时段内人类活动影响较小可忽略不计[15]。
3 实例验证 3.1 张南水道概况张南水道位于鄱阳湖区,上起九江市的锁江楼,下止八里江口,全长约30 km,平面形态为微弯双分汊河型,是长江中下游重点碍航浅滩水道之一。其中,左汊呈圆弧弓背状,称为北港;右汊相对顺直,称为南港,航程比北港短约6 km。南港内有官洲和新洲上下交错而立,出现2级分汊,南港下段有鄱阳湖水自右岸汇入。
张家洲南港下浅区航道整治工程于2004年7月15日全部建成,工程方案如图 2所示:①左岸6道丁坝,主要作用是巩固新洲边滩,阻止主流北移,适当束窄过渡段河宽,集中水流,冲刷航槽。②右岸梅家洲边滩建护滩带两道,防止官洲夹出流对梅家洲边滩的破坏。③右岸官洲尾滩缘护岸,防止边滩冲刷崩退。

|
图 2 整治工程示意 Fig.2 Schematic diagram of remediation project |
整治工程实施后,航道条件得到显著改善,官洲、梅家洲边滩变化不大,新洲边滩明显淤积增高、扩大,下浅区航道内普遍冲刷,达到了设计航道尺度。
3.2 数据来源水文数据选取自2005—2015年九江水文站数据,张南水道下浅区2005年以来的分流比、分沙比十分稳定。前9年数据作为训练样本,后2年数据作为测试样本,见表 1。
| 表 1 样本数据 Tab.1 Sample data |
在2005—2015年间,存在丰水丰沙(2012年)、少水少沙(2007年)、丰水少沙(2005年)、少水丰沙年(2006年),样本的多样性以及代表性得以保证。
3.3 验证过程核函数选取过程中,就训练样本对线性核函数、多项式核函数、RBF核函数、sigmoid核函数都分别进行了试算,结果如表 2所示,核函数选择多项式核函数以及RBF核函数,无论是均方误差(MSE)还是相关系数都明显优于其余二者,而多项式核函数相较于RBF核函数而言效果更佳,主要体现为R2表现更好,因此,选择多项式核函数作为本模型的核函数。
| 表 2 核函数表现 Tab.2 Performance of kernel functions |
通过多次试算,选取不灵敏参数ε=0.001, 惩罚常数C=50和核函数参数σ=0.2。
3.4 验证结果本文的SVM试验均基于MATLAB编程实现, 编程实现的基本思想算法参照SVM算法模型的原理及算法流程,得到的预测结果如表 3所示。
| 表 3 SVM,BP模型预测结果 Tab.3 Predicted results of SVM model and BP model |
选用上述参数后,训练样本的模拟精度较高,相对误差在1%~12%,0 m线最小宽度B0平均相对误差为4.1%,宽深比ζ平均相对误差为7.5%,模拟精度达到要求。
从检验样本预测结果看,SVM模型的实际预测精度较好,2014年和2015年预测的B0相对误差分别为4.3%和8.2%,ζ相对误差分别为0.6%和1.0%。
从本实例研究结果看,BP模型2014年和2015年预测B0相对误差分别为6.4%和21.8%,ζ相对误差分别为4.7%和5.8%。SVM算法与BP模型相比预测精度提高,2014年和2015年0 m线最小宽度预测精度分别提高32.8%和62.4%, 宽深比精度分别提高87.2%和82.8%。BP神经网络是一种按误差逆传播算法训练的多层前馈网络,能学习和存贮大量的输入-输出模式映射关系,无需事前揭示描述这种映射关系的数学方程;但是BP模型需要大量的数据样本供学习之用,在样本量小的情况下,预测精度较大样本情况低。支持向量机方法根据有限的样本信息在模型的复杂性和学习能力之间寻求最佳折中,专门针对有限样本的情况,因此更能反映样本量有限的束水攻沙功能指标预测中输入与输出之间的非线性映射。
4 结语从丁坝群作用机理出发,分析归纳已有的研究成果,提出了丁坝群功能指标确定的原则以及反映丁坝群功能的指标。将支持向量机技术引入丁坝群束水攻沙功能指标预测,建立了预测既有整治建筑物丁坝群功能的SVM模型。SVM模型可以较好地解决以往很多学习方法存在的小样本、过学习、局部最小等实际难题,在小样本数据下效果比BP神经网络预测方法好。
| [1] |
杨兰, 李国栋, 李奇龙, 等. 丁坝群附近流场及局部冲刷的三维数值模拟[J]. 水动力学研究与进展, 2016, 31(3): 372-378. ( YANG Lan, LI Guodong, LI Qilong, et al. 3D numerical simulation of flow field and local scour around spur dikes[J]. Chinese Journal of Hydrodynamics, 2016, 31(3): 372-378. (in Chinese)) |
| [2] |
孙志林, 倪晓静, 许丹. 丁坝周围流动图像与局部冲刷深度[J]. 浙江大学学报(工学版), 2017, 51(11): 2189-2196. ( SUN Zhilin, NI Xiaojing, XU Dan. Physics of flow and local scour depth around spur dikes[J]. Journal of Zhejiang University(Engineering Science), 2017, 51(11): 2189-2196. DOI:10.3785/j.issn.1008-973X.2017.11.013 (in Chinese)) |
| [3] |
韩林峰, 王平义, 刘怀汉, 等. 洪水作用下丁坝可靠度分析及剩余寿命预测[J]. 水利水运工程学报, 2013(6): 54-60. ( HAN Linfeng, WANG Pingyi, LIU Huaihan, et al. Analysis of spur dike reliability by the action of flood and evaluation of residual life[J]. Hydro-Science and Engineering, 2013(6): 54-60. DOI:10.3969/j.issn.1009-640X.2013.06.008 (in Chinese)) |
| [4] |
窦希萍, 王向明, 娄斌. 潮流波浪作用下丁坝坝头概化模型的冲刷试验[J]. 水利水运工程学报, 2005(1): 28-33. ( DOU Xiping, WANG Xiangming, LOU Bing. General scouring model test of dike's head under tidal currents and waves[J]. Hydro-Science and Engineering, 2005(1): 28-33. DOI:10.3969/j.issn.1009-640X.2005.01.005 (in Chinese)) |
| [5] |
熊建秋.水科学信息分析计算新方法及其应用[D].成都: 四川大学, 2006. (XIONG Jianqiu. New method and its application to water science information analysis and calculation[D]. Chengdu: Sichuan University, 2006. (in Chinese)) http://cdmd.cnki.com.cn/Article/CDMD-10610-2006189368.htm
|
| [6] |
常福田, 丰玮. 丁坝群合理间距的试验研究[J]. 河海大学学报, 1992, 20(4): 7-14. ( CHANG Futian, FENG Wei. Experiment at investigation of reasonable spacing among spur dikes[J]. Journal of Hohai University, 1992, 20(4): 7-14. DOI:10.3321/j.issn:1000-1980.1992.04.002 (in Chinese)) |
| [7] |
韩玉芳.丁坝的造床作用研究[D].南京: 南京水利科学研究院, 2003. (HAN Yufang. The scouring processes of riverbed around spur dikes[D]. Nanjing: Nanjing Hydraulic Research Institute, 2003. (in Chinese)) http://cdmd.cnki.com.cn/Article/CDMD-82306-2004030702.htm
|
| [8] |
ROBERT C, CASELLA G. Monte Carlo statistical methods[M]. Springer Verlag, 2004.
|
| [9] |
CORTES C, VAPNIK V. Support-vector networks[J]. Machine Learning, 1995, 20(3). |
| [10] |
SEBALD D J, BUCKLEW J A. Support vector machine techniques for nonlinear equalization[J]. IEEE Transactions on Signal Processing, 2000, 48(11): 3217-3226. DOI:10.1109/78.875477 |
| [11] |
VAPNIK V. The nature of statistical learning theory[M]. New York: Springer, 1998.
|
| [12] |
崔东文. 基于多元变量组合的回归支持向量机集成模型及其应用[J]. 水利水运工程学报, 2014(2): 66-73. ( CUI Dongwen. A regression support vector machine integrated model based on multivariate combinations and its application[J]. Hydro-Science and Engineering, 2014(2): 66-73. DOI:10.3969/j.issn.1009-640X.2014.02.011 (in Chinese)) |
| [13] |
熊建秋, 李祚泳. 基于支持向量机的水流挟沙力预测研究[J]. 水利学报, 2005(10): 1171-1175. ( XIONG Jianqiu, LI Zuoyong. Sediment-carrying capacity forecasting based on support vector machine[J]. Journal of Hydraulic Engineering, 2005(10): 1171-1175. DOI:10.3321/j.issn:0559-9350.2005.10.005 (in Chinese)) |
| [14] |
柳长源.相关向量机多分类算法的研究与应用[D].哈尔滨: 哈尔滨工程大学, 2013. (LIU Changyuan. Research and application on the multi-classification of relevance vector machine algorithm[D]. Harbin: Harbin Engineering University, 2013. (in Chinese)) http://cdmd.cnki.com.cn/Article/CDMD-10217-1014134103.htm
|
| [15] |
陈一梅, 徐造林. 基于神经网络的河道浅滩演变预测模型[J]. 水利学报, 2002(8): 68-72. ( CHEN Yimei, XU Zaolin. Model based on neural network for predicting the evolution of shoal in river[J]. Journal of Hydraulic Engineering, 2002(8): 68-72. DOI:10.3321/j.issn:0559-9350.2002.08.012 (in Chinese)) |
 2019
2019 