2. 武汉大学 水资源与水电工程科学国家重点实验室,湖北 武汉 430072;
3. 南京水利科学研究院 港口航道泥沙工程交通行业重点实验室,江苏 南京 210029;
4. 河海大学,江苏 南京 210098
桥梁下部结构对水流存在束狭作用,促使河床发生相应冲淤变化。建桥引起的河床变化可分为压缩冲刷和局部冲刷,压缩冲刷是指桥墩压缩断面后发生的普遍冲刷,包括天然河床冲刷和桥墩压缩水流引起的冲刷;局部冲刷是指在水流漩涡作用下桥墩周围河床形成的冲刷坑。目前,大量研究集中在桥墩局部冲刷[1-5],对压缩冲刷研究较少[6-8]。桥墩压缩冲刷使得桥址断面出现整体冲刷下切,对建筑物基础安全不利[9]。就长江中下游而言,三峡水库蓄水后,下泄沙量急剧减小,加剧了下游河床冲刷,因此在过江桥梁设计中,桥墩压缩冲刷预测是关键技术问题之一。
以往学者通过模型试验或野外实测分析,得到桥墩压缩冲刷预测经验公式,其中较为著名的有:铁路及公路规范64-1式、64-1修正式和64-2简化式[10-11],美国HEC-18式[12],但此类公式只能反映某一水沙条件持续作用下压缩冲刷平衡值,且系数存在不确定性。近年来,国内外学者开始采用水沙数模预测桥墩压缩冲刷。刘有录等[13]通过调整桥墩附近网格局部水头损失系数,模拟了百年一遇特大洪水期间黄河中游某铁路桥墩冲刷,床面冲淤趋势与试验基本吻合,但具体量值存在差异;Lai等[6-9, 14]对长压缩段矩形水槽试验进行了验证,得出模型可较好地模拟沿程水位变化及压缩段冲刷分布,但未考虑上游泥沙过程及悬沙造床作用。对于长江下游而言,三峡水库蓄水拦沙使得下泄的水沙过程明显有别于天然情况。下游河床冲淤复杂,相比于过江隧道[15-16],桥墩压缩冲刷影响因素较多,因此要想较好地预测桥墩压缩冲刷,模型需具备以下几方面条件:①选取合理水沙过程;②模型参数需进行多次率定和验证,能复验河道年内和年际冲淤变化;③能较好反映建桥前后水流泥沙运动。
本文以新建连云港至镇江铁路世业洲大桥桥位方案为背景,对桥墩压缩冲刷模型的建立、参数验证、桥墩边界处理、水沙过程选取、冲刷深度预测等进行研究,为类似问题的研究提供参考。
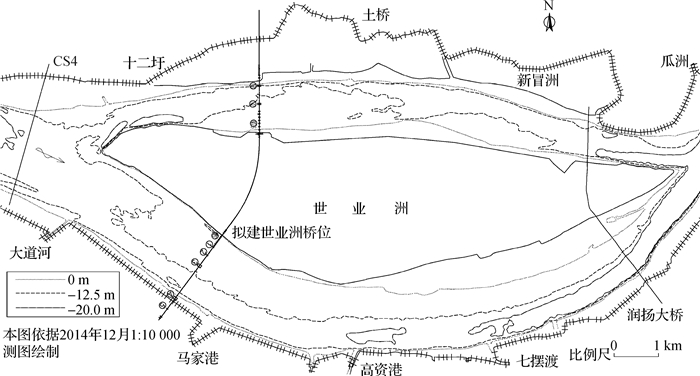
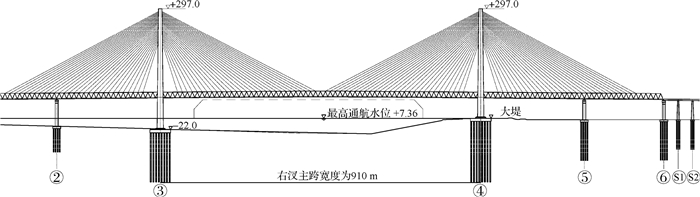
1 工程概况新建的连云港至镇江铁路全长249 km,北承新长铁路,中联宁启铁路,南与京沪高铁、沪宁城际铁路相接,是连接苏北、苏中、苏南地区的南北纵向铁路主通道。铁路拟在长江世业洲至五峰山河段处跨越长江,过江通道拟采用跨江桥梁,根据桥梁位置的不同,分为世业洲桥位、五峰山桥位方案。其中,世业洲桥位方案为:桥址位于世业洲中上部,采用悬索桥方案,左汊主跨为406 m,右汊主跨为910 m。平面、立面布置及桥墩结构布置见图 1~2。
|
图 1 世业洲桥位方案平面布置 Fig.1 Plan layout of Shiyezhou bridge location scheme |
|
图 2 桥墩立面布置(世业洲右汊)(单位:m) Fig.2 Elevation layout of piers (right branch of Shiyezhou)(unit: m) |
世业洲河段为微弯分汊河型,江中有世业洲将河道分为左右两汊,见图 1。左汊为支汊,2012年12月实测分流比为38.8%,右汊为主汊。由于河道有良好的进出口节点控制及岸线守护作用,总体河势变化不大,但局部区域演变仍较为明显。主要表现为汊道分流格局变化及洲滩冲淤调整。
(1) 汊道分流格局变化主要是左汊分流比增加,右汊分流减小。20世纪70年代中期至90年代初期,左汊分流比缓慢增加,年均增幅为0.1%;1995年后,受到连续大洪水作用,增幅速度明显加大,其中1997—1999年,年均增大达2.8%;2000年以后增速趋缓。世业洲左汊分流比由20世纪70年代的20%增至40%左右。
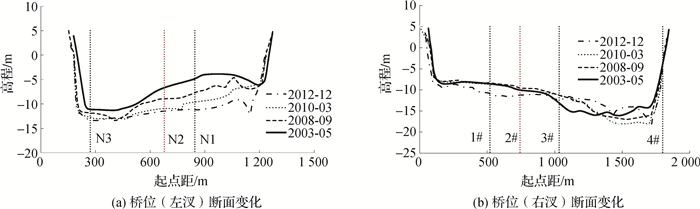
(2) 洲滩冲淤调整体现为世业洲头低滩持续冲刷后退;左汊整体冲刷,局部位置冲深幅度4 m;世业洲右汊进口段左侧边滩冲刷、右侧深槽淤积,中下段则表现为世业洲右缘边滩淤长,深槽冲刷。桥址断面冲淤变化见图 3。
|
图 3 世业洲桥位桥址断面多年冲淤变化 Fig.3 Changes in erosion and siltation at site section of Shiyezhou bridge over years |
正交曲线坐标系下的平面二维水沙数模控制方程组如下:
(1) 水流连续方程:
| $ \frac{\partial Z}{\partial t}+\frac{1}{C_{\xi} C_{\eta}}\left[\frac{\partial\left(C_{\eta} H u\right)}{\partial \xi}+\frac{\partial\left(C_{\xi} H v\right)}{\partial \eta}\right]=0 $ | (1) |
(2) 水流运动方程:
| $ \begin{array}{l} \frac{{\partial (Hu)}}{{\partial t}} + \frac{1}{{{C_\xi }{C_\eta }}}\left[ {\frac{\partial }{{\partial \xi }}\left( {{C_\eta }Huu} \right) + \frac{\partial }{{\partial \eta }}\left( {{C_\xi }Hvu} \right) + Hvu\frac{{\partial {C_\xi }}}{{\partial \eta }} - H{v^2}\frac{{\partial {C_\eta }}}{{\partial \xi }}} \right] = - \frac{{gu/{u^2} + {v^2}}}{{{C^2}}} - \frac{{gH}}{{{C_\xi }}}\frac{{\partial Z}}{{\partial \xi }} + \\ \frac{1}{{{C_\xi }{C_\eta }}}\left[ {\frac{\partial }{{\partial \xi }}\left( {{C_\eta }H{\sigma _{\xi \xi }}} \right) + \frac{\partial }{{\partial \eta }}\left( {{C_\xi }H{\sigma _{n\xi }}} \right) + H{\sigma _{\xi \eta }}\frac{{\partial {C_\xi }}}{{\partial \eta }} - H{\sigma _{\eta \eta }}\frac{{\partial {C_\eta }}}{{\partial \xi }}} \right] \end{array} $ | (2) |
| $ \begin{array}{l} \frac{{\partial (Hv)}}{{\partial t}} + \frac{1}{{{C_\xi }{C_\eta }}}\left[ {\frac{\partial }{{\partial \xi }}\left( {{C_\eta }Huv} \right) + \frac{\partial }{{\partial \eta }}\left( {{C_\xi }Hvv} \right) + Huv\frac{{\partial {C_\eta }}}{{\partial \xi }} - H{u^2}\frac{{\partial {C_\xi }}}{{\partial \eta }}} \right] = - \frac{{gv/{u^2} + {v^2}}}{{{C^2}}} - \frac{{gH}}{{{C_\eta }}}\frac{{\partial Z}}{{\partial \eta }} + \\ \frac{1}{{{C_\xi }{C_\eta }}}\left[ {\frac{\partial }{{\partial \xi }}\left( {{C_\eta }H{\sigma _{\xi \eta }}} \right) + \frac{\partial }{{\partial \eta }}\left( {{C_\xi }H{\sigma _{\eta \eta }}} \right) + H{\sigma _{n\xi }}\frac{{\partial {C_\eta }}}{{\partial \xi }} - H{\sigma _{\xi \xi }}\frac{{\partial {C_\xi }}}{{\partial \eta }}} \right] \end{array} $ | (3) |
式中:(ξ, η)为曲线坐标系坐标;(x, y)为物理坐标;Cξ,Cη分别为ξ, η方向拉梅系数;u,v分别为ξ,η方向流速分量;Z为水位;t为时间;H为水深;C为谢才系数,
(3) 悬移质不平衡输移方程:
| $ \begin{array}{l} \frac{{\partial \left( {H{S_i}} \right)}}{{\partial t}} + \frac{1}{{{C_\xi }{C_\eta }}}\left[ {\frac{\partial }{{\partial \xi }}\left( {{C_\eta }Hu{S_i}} \right) + \frac{\partial }{{\partial \eta }}\left( {{C_\xi }Hv{S_i}} \right)} \right] = \frac{1}{{{C_\xi }{C_\eta }}}\left[ {\frac{{{\varepsilon _\xi }}}{{{\sigma _s}}}\frac{{{C_\eta }}}{{{C_\xi }}}\frac{{{C_\eta }}}{{{C_\xi }}}H\frac{{\partial {S_i}}}{{\partial \xi }}} \right) + \\ \frac{\partial }{{\partial \eta }}\left( {\frac{{{\varepsilon _\eta }}}{{{\sigma _s}}}\frac{{{C_\xi }}}{{{C_\eta }}}H\frac{{\partial {S_i}}}{{\partial \eta }}} \right)] + {\alpha _i}{\omega _i}\left( {S_i^* - {S_i}} \right) \end{array} $ | (4) |
式中:αi为泥沙的含沙量恢复饱和系数;ωi为第i组泥沙沉速;Si为第i组悬移质含沙量;Si*为第i组悬移质挟沙力,εξ,εη分别为ξ,η方向泥沙扩散系数;σs取常数1.0。
(4) 推移质不平衡输移方程:
| $ \frac{{\partial H{S_{{\rm{b}}L}}}}{{\partial t}} + \frac{1}{{{C_\xi }{C_\eta }}}\left[ {\frac{\partial }{{\partial \xi }}\left( {{C_\eta }Hu{S_{{\rm{b}}L}}} \right) + \frac{\partial }{{\partial \eta }}\left( {{C_\xi }Hv{S_{{\rm{b}}L}}} \right)} \right] = {\alpha _{{\rm{b}}L}}{\omega _{{\rm{b}}\mathit{L}}}\left( {S_{{\rm{b}}L}^* - {S_{{\rm{b}}L}}} \right) $ | (5) |
式中:SbL*为第L组推移质挟沙能力;SbL为第L组推移质含沙浓度;αbL为第L组推移质恢复饱和系数;ωbL为第L组推移质的沉速。
(5) 河床变形方程:
| $ 悬移质冲淤引起的河床变形:\;\;\;\;\;\;\;{\gamma _{0i}}\frac{{\partial {Z_i}}}{{\partial t}} = {\alpha _i}{\omega _i}\left( {{S_i} - S_i^*} \right) $ |
| $ 推移质冲淤引起的河床变形:\;\;\;\;\;\;\;{\gamma _{0{\rm{b}}L}}\frac{{\partial {Z_{{\rm{b}}L}}}}{{\partial t}} = {\alpha _{{\rm{b}}\mathit{L}}}{\omega _{{\rm{b}}L}}\left( {{S_{{\rm{b}}L}} - S_{{\rm{b}}L}^*} \right) $ |
| $ 河床总的冲淤厚度为:\;\;\;\;\;\;\;Z = \sum\limits_{i = 1}^M {{Z_i}} + \sum\limits_{L = 1}^N {{Z_L}} $ | (6) |
式中:M为悬移质分组数;N为推移质分组数;γ0i为i组悬移质泥沙干重度;Zi为第i组悬移质引起的河床冲淤厚度;γ0bL为L组推移质泥沙干重度;ZL为第L组推移质引起的河床冲淤厚度;Z为河床总冲淤厚度。
2.2 模型设置为数值求解水流运动方程组(1)~(3),采用积分守恒的控制体积法离散方程,并利用SIMPLER方程式求解耦合方程,反复迭代直到流场收敛;对悬移质输移方程(4)和推移质输移方程(5)在离散后采用欠松驰技术及逐行扫描的TDMA技术隐式求解;对河床变形方程(6)采用有限差分离散,显式求解。
水流运动方程主要参数有:糙率n和紊动黏性系数νt。糙率反映了天然河流的阻力,可通过与实测水位及流速验证确定;紊动黏性系数
泥沙运动方程主要参数有:悬移质分组挟沙能力Si*、推移质分组输沙率gbL*,其中悬移质分组挟沙能力Si*=P*S*,P*为分组挟沙力级配(P*可根据文献[15]附录B提供的方法确定),S*为水流总的挟沙力,一般采用张瑞瑾公式确定:
| $ S_{*}=k\left(\frac{\sqrt{u^{2}+v^{2}}}{g h \omega}\right)^{m} $ | (7) |
式中:ω为泥沙平均沉速;k,m为系数。推移质分组输沙率
以往计算中主要采用局部地形修正、附加糙率等方法概化桥墩,但此类方法仅能模拟桥墩阻水效应,无法给出桥墩附近细部流场变化,因而也无法计算桥墩压缩冲刷。随着计算机性能和数值方法的提高,可采用加密网格法处理桥墩,使得网格与桥墩尺度一致。如何处理桥墩边界是准确模拟桥墩附近水沙运动的关键,根据模拟空间尺度不同,可分为小尺度和大尺度两类模型。

|
图 4 桥墩边界处理示意 Fig.4 Schematic diagram of bridge pier boundary treatment |
小尺度模型通常用于实验室桥墩模拟,网格尺度较小,为厘米级,桥墩边界可采用大系数法与壁面率相结合的方法进行处理,即桥墩内的网格(图 5中网格节点1~16所围的内部网格)采用大系数法处理,亦即在计算时,令其源项为一大系数,则其计算结果为0;而与桥墩壁面相邻的网格节点(网格节点1~13)则采用壁面率进行处理。

|
图 5 模型水位与流速验证结果 Fig.5 Verification results of water level and flow velocity given by model |
大尺度模型通常用于天然河道中桥墩模拟。河道边界复杂,网格尺度一般为米级别,采用壁面率时,壁面第一个计算节点与壁面间的距离为
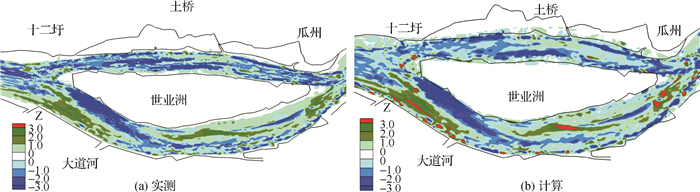
建立了世业洲河段平面二维水沙模型,模型范围上迄三江口,下至六圩河口,模拟河段全长约40 km。为提高模型预测精度,对模型参数进行了反复率定及验证。图 5为沿程水位和典型断面流速的验证结果。限于篇幅,这里仅给出中长期河床冲淤验证。模型采用2011年10月地形作为初始地形,2015年11月作为验证地形。进口流量和含沙量过程采用大通站实测资料,出口水位由镇江站水位流量关系曲线得到。模型验证了河段经过4个完整水文年后的河床冲淤。由图 6可见,计算与实测冲淤部位和冲淤分布符合较好。
|
图 6 河段实测与计算冲淤分布对比(2011年10月—2015年11月)(单位:m) Fig.6 Comparison between measured and calculated riverbed scouring and silting distribution along Shiyezhou reach (from Oct.2011 to Nov.2015)(unit:m) |
预测成果合理性与水沙过程的选取密切相关。针对长江下游河段来水来沙特点,考虑三峡水库蓄水后长江下游水文控制站(大通)水沙变化,从偏安全的角度出发,提出水沙过程的确定方法。
(1) 特大洪水年水沙过程:根据世业洲桥位方案的设计标准(100年一遇洪水设计,300年一遇洪水校核),选取300年一遇洪水作为特大洪水年。其中,流量过程是以1998年(100年一遇)为基础,根据频率对洪峰流量进行放大;沙量过程则根据三峡水库蓄水后大通站流量和输沙率关系曲线,从工程安全角度出发,采用下包线推求特大洪水年所对应的沙量过程(见图 7)。

|
图 7 三峡水库蓄水后大通站流量与输沙率关系 Fig.7 Relationships between discharge and sediment-transport rate at Datong station after impoundment of Three Gorges reservoir |
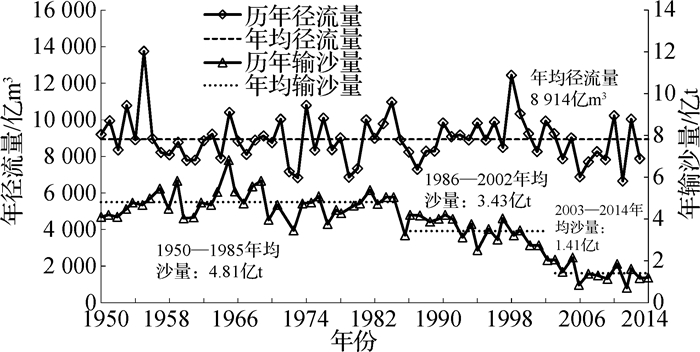
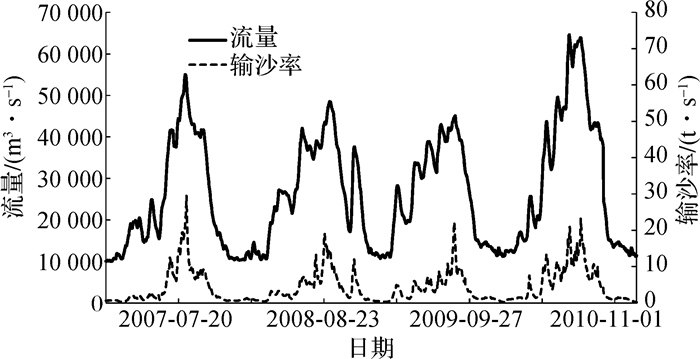
(2) 系列水文年水沙过程:采用典型系列年,并考虑特大洪水年的组合。根据大通站1950—2014年水沙资料,三峡水库蓄水以来大通站流量变化不大,且多为中小水年,但输沙量明显小于蓄水前,这一变化反映了三峡水库的蓄水拦沙作用。三峡水库蓄水前,大通站多年输沙量为4.27亿t,蓄水后,2004—2014年均输沙量为1.43亿t,较蓄水前减少了66%(图 8)。2007—2010年能较好地代表三峡建库后2004—2014年水沙特点;据统计2007—2010年径流量为8 372亿m3,与三峡建库后平均径流量8 321亿m3基本相当,年最大流量为64 600 m3/s,最小流量为10 000 m3/s,见图 9。考虑到1998年大洪水的影响,最终确定系列水文年为2007—2010年+1998年(沙量过程用图 7下包线)。
|
图 8 1950—2014年大通站年径流量、输沙量 Fig.8 Annual runoff and sediment runoff by Datong station from 1950 to 2014 |
|
图 9 2007—2010年流量输沙率过程 Fig.9 Process of discharge and sediment-transport rate from 2007 to 2010 |
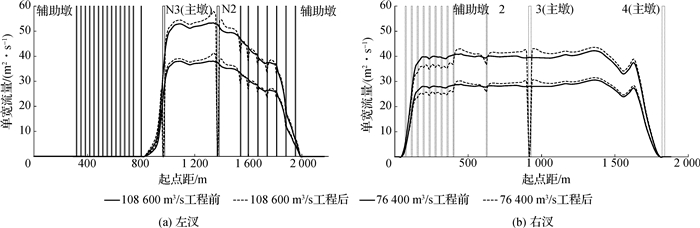
桥梁建设引起桥区一定范围内水位与流速分布变化,二者将直接影响到桥址断面单宽流量分布。一般而言,建桥后桥墩间单宽流量有所增加(见图 10),桥墩上下游受墩柱壅水及掩护影响,单宽流量有所减小。在世业洲右汊左侧,由于桥墩间距较小,阻力较大,使得桥墩间单宽流量减小,同时右侧河道单宽流量增幅较大。
|
图 10 桥址断面单宽流量横向分布 Fig.10 Transverse distribution of unit discharge of bridge site sections |
遭遇特大洪水年后,桥位上游由于桥墩阻水作用,流速减小,河床以淤积为主;桥位下游受桥墩挤压水流和掩护作用,河床有冲有淤;桥位断面,因桥墩存在,过水面积缩窄,单宽流量增加,出现压缩冲刷,其中冲刷幅度较大的位置是左汊N3#桥墩(9.46 m)和N2#桥墩(5.92 m),右汊桥址断面冲刷相对较小,2#辅助墩桥墩2.81 m,3#主墩3.70 m。
文献[17]采用1998年和2013年长江下游大通—吴淞口航行图,对长江下游典型桥梁桥址断面压缩冲刷进行统计(见表 1),可见,因桥址所处位置和断面形态不一,各桥压缩冲刷深度有所差异,幅度在2.6~8.0 m之间,与世业洲桥位模型预测结果相当。
| 表 1 长江下游典型桥梁桥址断面最大压缩冲刷深度实测统计(1998—2013年) Tab.1 Maximum compression scouring depths of typical bridge site sections in lower reaches of Yangtze River (1998-2013) |
(1) 建立了桥墩压缩冲刷预测模型,对小尺度模型,桥墩边界可采用大系数法与壁面律相结合方法; 对天然大尺度模型,壁面率无法适用,可直接在桥墩壁面上规定不可入条件及无滑动条件。模型参数进行多次率定和验证,具备复验河道年内和年际冲淤变形的能力。
(2) 针对长江下游河段水沙特点,考虑三峡水库蓄水以来大通站水沙条件变化,从工程安全角度出发,提出水沙条件的确定方法,并确定不利水沙过程。
(3) 受桥墩影响,桥位断面出现压缩冲刷,其中冲刷幅度较大的位置是左汊N3#桥墩(9.46 m)和N2#桥墩(5.92 m),右汊桥址断面冲刷相对较小。通过对长江下游典型桥梁桥址断面压缩冲刷深度统计可见,冲刷幅度在2.6~8.0 m,与模型预测结果基本相当。
| [1] |
OLSEN N R B, KJELLESVIG H M. Three-dimensional numerical flow modeling for estimation of maximum local scour depth[J]. Journal Hydraulic Research, 1998, 36(4): 579-590. DOI:10.1080/00221689809498610 |
| [2] |
KARIM O A, ALI K H M. Prediction of flow patterns in local scour holes caused by turbulent water jets[J]. Journal Hydraulic Research, 2000, 38(4): 279-287. DOI:10.1080/00221680009498327 |
| [3] |
ROULUND A, SUMER B M, FREDSOE J, et al. Numerical and experimental investigation of flow and scour around a circular pile[J]. Journal Fluid Mech, 2005, 534: 351-401. DOI:10.1017/S0022112005004507 |
| [4] |
陈小莉.局部绕流冲刷机理及数值模拟研究[D].北京: 清华大学, 2008. (CHEN Xiaoli. Study on mechanics and numerical simulation of flow and local scour around hydraulic structures[D]. Beijng: Tsinghua University, 2008. (in Chinese))
|
| [5] |
SUMER B M, WITHEHOUSE R J S, TORUM A. Scour around coastal structures: a summary of recent research[J]. Coastal Engineering, 2001, 44(2): 153-190. |
| [6] |
LAI Y G, GREIMANN B P. Predicting contraction scour with a two-dimensional depth-averaged model[J]. Journal of Hydraulic Research, 2010, 48(3): 383-387. DOI:10.1080/00221686.2010.481846 |
| [7] |
FENOCCHI A, NATALE L. Using numerical and physical modeling to evaluate total scour at bridge piers[J]. Journal of Hydraulic Engineering, 2016, 142(3): 06015021. DOI:10.1061/(ASCE)HY.1943-7900.0001096 |
| [8] |
郭辉, 齐梅兰. 跨河桥梁压缩冲刷数值模拟研究[J]. 中国铁道科学, 2011, 32(5): 43-49. ( GUO Hui, QI Meilan. Numerical simulation study on the contraction scour of bridge cross the river[J]. China Railway Science, 2011, 32(5): 43-49. (in Chinese)) |
| [9] |
郭辉.桥渡压缩冲刷数值模拟研究[D].北京: 北京交通大学, 2013. (GUO Hui. Numerical study of contraction scour at bridge crossings[D]. Beijing: Beijing Jiaotong University, 2013. (in Chinese)) http://cdmd.cnki.com.cn/Article/CDMD-10004-1013341998.htm
|
| [10] |
TB 10017—1999铁路工程水文勘测设计规范[S]. (TB 10017—1999 Code for survey and design on hydrology of railway engineering[S]. (in Chinese))
|
| [11] |
JTG C30—2002公路工程水文勘测设计规范[S]. (JTG C30—2002 Hydrological specifications for survey and design of highway engineering[S]. (in Chinese))
|
| [12] |
SHIROLE A M, HOLT R C. Planning for comprehensive bridge safety assurance program (Transport Research Report No.1290)[R]. Washington D C: Transportation Research Board, 1991: 137-142.
|
| [13] |
刘有录, 褚衍东. 桥渡全沙冲淤数值模拟[J]. 铁道学报, 1993, 15(4): 96-102. ( LIU Youlu, CHU Yandong. Numerical modelling of scouring and silting of full sediment in the bridge reach[J]. Journal of the China Railway Society, 1993, 15(4): 96-102. DOI:10.3321/j.issn:1001-8360.1993.04.013 (in Chinese)) |
| [14] |
DUE B M, RODI W. Numerical simulation of contraction scour in an open channel[J]. Journal of Hydraulic Engineering, 2008, 134(4): 367-377. DOI:10.1061/(ASCE)0733-9429(2008)134:4(367) |
| [15] |
张为, 李义天, 袁晶. 长江下游过江隧道河段最大冲刷深度预测研究[J]. 水力发电学报, 2011, 30(4): 90-97. ( ZHANG Wei, LI Yitian, YUAN Jing. Prediction of maximum bed erosion depth near a crossing tunnel under the lower reach Yangtze River[J]. Journal of Hydroelectric Engineering, 2011, 30(4): 90-97. (in Chinese)) |
| [16] |
魏帅, 李国禄, 陈述. 长江下游过江隧道河段最大冲深数值模拟[J]. 水利水运工程学报, 2016(1): 1-8. ( WEI Shuai, LI Guolu, CHEN Shu. Mathematical model studies on maximum bed erosion depth near Shiyezhou river-crossing tunnel[J]. Hydro-Science and Engineering, 2016(1): 1-8. (in Chinese)) |
| [17] |
陆雪骏.长江感潮河段桥墩冲刷研究[D].上海: 华东师范大学, 2016. (LU Xuejun. Research on the local scour at bridge piers in the tidal reach of the Changjiang River[D]. Shanghai: East China Normal University, 2016. (in Chinese)) http://cdmd.cnki.com.cn/Article/CDMD-10269-1016137824.htm
|
2. State Key Lab of Water Resources and Hydropower Engineering Science, Wuhan University, Wuhan 430072, China;
3. Key Laboratory of Port, Waterway and Sedimentation Engineering of the Ministry of Transport, Nanjing Hydraulic Research Institute, Nanjing 210029, China;
4. Hohai University, Nanjing 210098, China
 2019
2019 