2. 南京水利科学研究院,江苏 南京 210029
潮汐不对称性指潮波波形上的不对称。研究潮汐不对称对于海湾、河口地区的余流、物质输运和地形演变等都具有重要意义。20世纪80年代左右,Aubrey等[1-2]发现, 潮波进入河口与海岸地区后会由于浅水效应产生不对称性,天文潮之间的相互作用和天文潮与浅水分潮的相互作用都会对其产生影响。Friedrichs等[3]提出使用M4与M2分潮的振幅比来计算潮汐不对称性的大小,并用其相位差来定义方向。在浅水分潮并不明显的海域,Hoitink等[4]提出将O1,K1分潮合成后与M2比较来衡量不对称性的计算方法。Nidzieko提出可以用水位对时间导数的偏度来定量分析不对称性[5]。根据这些方法,国内外学者对潮汐不对称性进行了一些研究[6-9],成果主要集中在浅水分潮作用相对强烈的河口地区,对于浅水分潮弱的开敞式圆弧形海湾的潮汐不对称性研究尚少。
海南省红塘湾海域属典型开敞式弧形海湾。近些年来,修建了临空产业园人工岛,未来可能建造其他人工岛,会对红塘湾海域水动力结构产生影响,因此了解现有条件下的水动力特征是必要的。目前,已有学者对该海域的波浪与冲淤特征进行研究[10-11],但是尚缺少潮汐特征研究。本文利用海南红塘湾实测潮位资料,应用偏度与复分析方法,分析天文潮占主导的开敞式海湾潮汐不对称性分布机制,为该海域余流、物质净输运等提供动力基础。
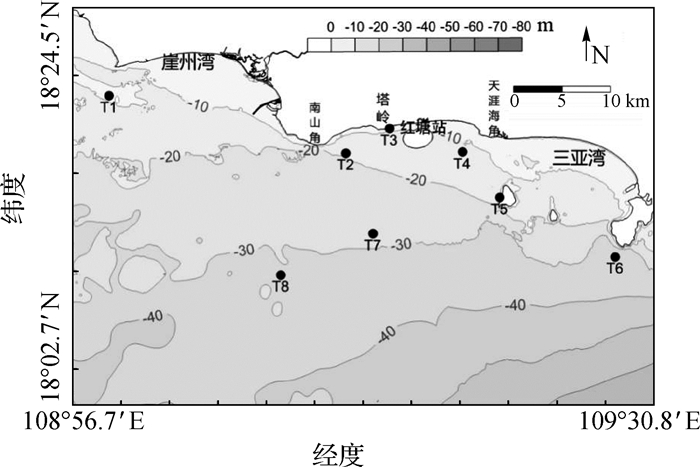
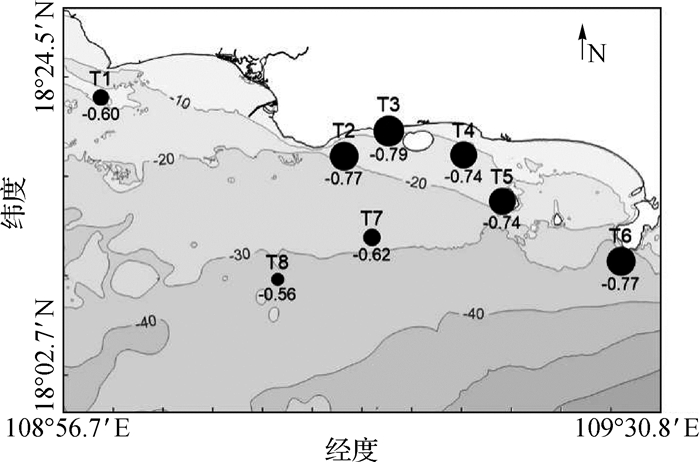
1 研究区域与资料来源红塘湾位于海南省三亚市西侧,东接三亚湾,西接崖州湾。该地区属典型的砂质海岸,地形及等深线见图 1,岸外0~10 m海底坡度相对较陡,地形呈西北高东南低的走势。目前该段海岸整体表现为冲刷,波浪是该海岸侵蚀的主要动力,其中西段冲刷强于东段。海湾周边无明显的泥沙供给,海外无掩护,属于典型开敞弧形海湾。海域3—4月盛行东南风,5—8月偏西南风,9—12月以东北风为主,全年月平均风速在2 m/s以下。
|
图 1 红塘湾地形与潮位测站 Fig.1 Topography of Hongtang bay and tidal level gauging stations |
实测资料包括红塘潮位站2016年3月1日0:00至2017年3月31日23:00的连续观测潮位数据与8个临时潮位站在2016年8月9日10:00时至20日13:00大、中、小全潮期间的潮位数据。临时潮位站根据《水运工程测量规范》(JTS 131—2012)布置并确立潮高基准面,选址主要考虑了水深及地形变化,分别在离岸方向与沿岸方向上以及岛屿附近选择了特征点。潮位利用TGR-2050潮位仪测量,观测数据经与自动气象站气压数据订正后,利用水准联测数据订正到国家85高程基准面上。分析所采用的潮位数据频率为1次/h。各潮位观测站如图 1,红塘潮位观测站设于红塘湾沿岸的109°15.293′E和18°17.939′N处,T1在西侧的崖州湾海域,T5在西瑁洲岛西侧,T6在东侧鹿回头半岛南侧,T2,T3,T4分布在湾内,T7,T8在外海区域,红塘潮位观测站与T3站接近。
潮位资料分析采用调和分析方法,以平衡潮理论为基础,将实际潮位视为各分潮叠加的结果,利用最小二乘法使调和潮位尽量接近实际潮位,求得各分潮调和常数;计算过程利用Pawlowicz等[12]编写的T-tide程序包进行,其以时间序列分析为理论基础,采用Gram-Schmidt数值计算方法对方程组进行求解。
2 红塘湾潮汐不对称现象 2.1 潮汐基本特征为直观判断红塘湾海域潮汐特征,根据红塘潮位站全年的资料进行统计分析,得到潮汐部分特征值,平均潮位为0.55 m,平均潮差为0.77 m,平均涨潮潮差0.66 m,平均落潮潮差0.89 m,最大潮差为1.96 m,最高潮位为1.84 m,最低潮位为-0.41 m,平均涨潮历时为6.78 h,平均落潮历时为5.46 h。涨潮历时长于落潮历时,而平均涨潮潮差小于平均落潮潮差,显然落潮期间潮动力更为明显,从而判断该海域为落潮优势。
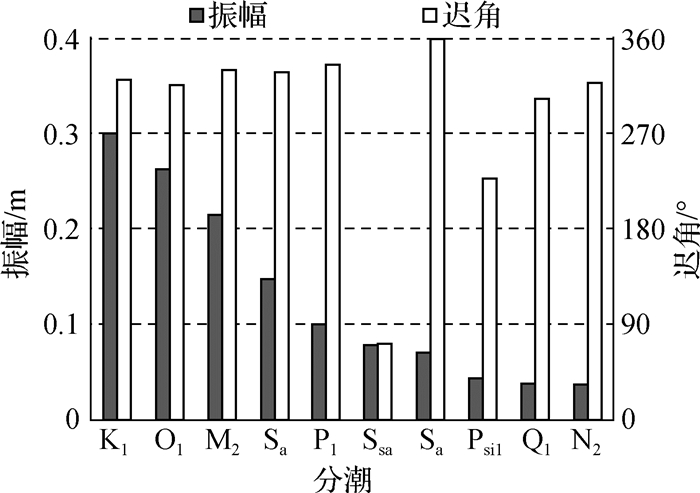
2.2 潮汐调和常数分布根据红塘湾潮位站全年的资料计算,得到该地区各主要分潮的振幅和迟角如图 2所示,可以看出该海域由全日分潮K1,O1与半日分潮M2主导,而浅水分潮振幅很小,这主要是由于本区域地形开阔、没有同河口一样的收缩影响,且没有径流,水动力环境与河口地区相比相对简单。根据K1,O1分潮振幅之和与M2分潮振幅的比值2.68,可判断出该海域潮汐为不规则全日潮。
|
图 2 主要分潮调和常数 Fig.2 Harmonic constants of main tidal constituents |
图 3为测量得到的各临时测站O1,K1,M2振幅及迟角。为方便表示,将O1,K1和M2的振幅都减去20 cm,迟角各减去150°,200°和80°,可以看出除T8外,各测站振幅为K1>O1>M2。各站的分潮潮幅显示,红塘湾及毗邻海域的O1,K1,M2振幅分布总体与等深线和离岸线距离有关。靠近岸侧,O1,K1和M2各分潮潮幅总体有所增大。离岸远且水深大的T8处,得到O1,K1分潮的最小值; T7处得到M2分潮的最小值; T1~T6各站越接近岸线,水深越浅,O1,K1,M2分潮振幅基本呈增加趋势。各分潮的迟角沿着涨潮方向逐渐增加,从T6到T1的变化接近20°。红塘湾湾内的T2,T3,T4测站与西瑁洲岛西边的T5测站的调和常数无太大差别。

|
图 3 红塘湾海域各测站主要分潮调和常数分布 Fig.3 Distribution of harmonic constants of main tidal constituents |
根据Nidzieko提出的方法[5],可以利用偏度计算潮汐不对称性,偏度γ计算如下:
| $ \gamma = \left( {\frac{1}{{N - 1}}\sum\limits_{i = 1}^N {{{\left( {{x_i} - \bar x} \right)}^3}} } \right)/{\left[ {\frac{1}{{N - 1}}\sum\limits_{i = 1}^N {{{\left( {{x_i} - \bar x} \right)}^2}} } \right]^{\frac{3}{2}}} $ | (1) |
式中:xi为水位对时间的导数;N为序列长度。γ为正,代表涨潮优势,反之则落潮优势,如此即可量化潮汐不对称性。
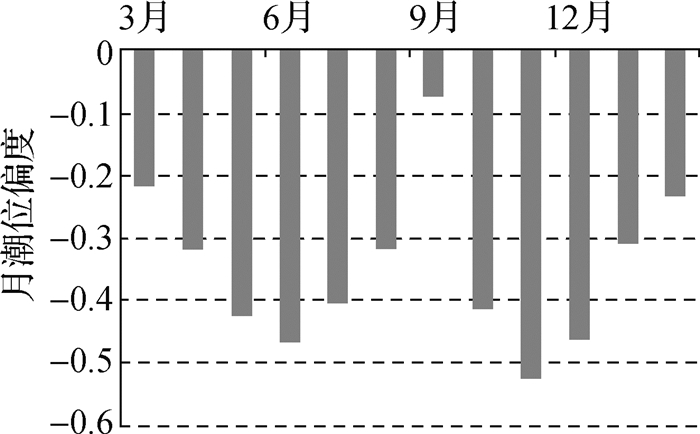
采用红塘潮位站1年潮位资料计算γ值(图 4)。由此可见红塘湾潮汐不对称在时间上具有明显的半年周期性变化特征,且落潮总是占优,与2.1节中判断一致,落潮优势在春、秋季逐渐增强,夏、冬季逐渐减弱。另外,不对称性全年最小值在9月,涨落潮大致相当,不对称性极大值出现在6月与10月。根据Jewell的研究[13],当K1与S2分潮作用都较强时,潮汐不对称性的半年性周期变化主要由K1与S2分潮的频率差引起。具体来说,根据Doodson[14]的引潮势展开,K1的频率为ω1+ω2,S2的频率为2ω1+2ω2-2ω3,其中ω1, ω2, ω3分别指地球相对月球自转的角频率、月球公转角频率与平太阳在天赤道上运行的角频率,2个正弦波叠加后会在长周期上产生1个频率为2ω3的波动,周期为半个回归年,即182.6 d左右。在该海域主要分潮中,频率与ω3有关的还有P1,但并不能通过与其他主要分潮叠加进而对不对称性产生影响,因此判断长周期上不对称性的变化主要由K1与S2分潮相互作用引起。
|
图 4 红塘站全年逐月偏度γ值 Fig.4 Monthly variation of γ for one year at Hongtang station |
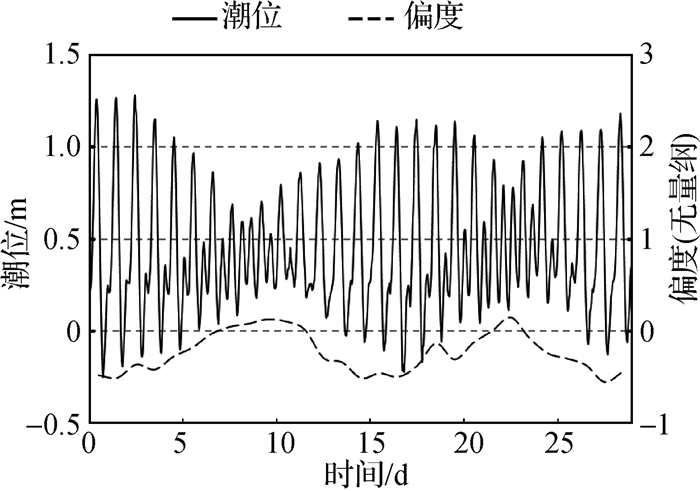
利用红塘站8月的逐时潮位资料,计算潮汐不对称性变化值,γ值随潮位变化过程见图 5。可以看出潮汐不对称性在大小潮期间有着明显的周期性波动,且与潮位变化相吻合,在大多数时间为落潮优势,大潮时最为明显,而在小潮前后的一两天为涨潮占优且优势不明显。
|
图 5 红塘站8月偏度γ值随潮位变化过程 Fig.5 γ and tide level process lines in August at Hongtang bay station |
采用同样方法计算红塘湾T1~T8临时潮位观测站潮汐不对称性(图 6),负值代表落潮优势。各站潮汐不对称性偏度值显示,各测站均为落潮优势,只是偏度值各站有所差异,T7和T8测站偏度明显小于近岸处的测站。离岸较近的测站中,湾内的T2,T3,T4测站由于水深相近不对称性也相近,受西瑁洲岛影响,潮汐不对称性在T5处最为明显。分析其原因,外海分潮振幅较小,类似深水波,传播至近岸,水深变浅,波浪呈浅水波型,因此海床底摩阻作用增强。由此可以推断,水深与地形为该海域潮汐不对称性的重要影响因子。

|
图 6 红塘湾各潮位站γ值分布 Fig.6 Distribution of γ values of Hongtang baystations |
红塘湾属开敞式弧形海湾,在水动力环境、地形、分潮组合等方面与河口有较大差异。对比前人在瓯江口、长江口等潮汐不对称性方面的研究成果[9, 15],开敞式的红塘湾海域潮汐不对称性在数值与时间变化幅度上均较小,呈现出更明显的规律性; 除此之外也有许多相似点,如不对称性的半月、季节变化。为探明红塘湾海域潮汐不对称性的机理,将从分潮组合对不对称性的贡献、不对称性的大小潮变化以及地形因素对潮汐不对称性影响3个方面探讨分析。
3.1 分潮组合对不对称性贡献采用Song在Nidzieko研究基础上改进的方法[16],利用调和常数可直接计算其中不同分潮组合引起的潮汐不对称性,同时比较不同分潮组合相互作用对潮汐不对称性的贡献。根据其理论,在二阶非线性条件下,只有当2个分潮的频率满足2ω1=ω2或3个分潮的频率满足ω1+ω2=ω3时, 它们的相互作用才能引起潮汐的不对称性。分别以β2,β3代表 2个与3个分潮组合得到的不对称性值,以a,φ和ω分别指组合中对应分潮的振幅、迟角与频率,具体算法如下:
| $ {\beta _2} = \frac{3}{4}a_1^2\omega _1^2{a_2}{\omega _2}\sin \left( {2{\varphi _1} - {\varphi _2}} \right)/{\left( {\frac{1}{2}\sum\limits_{i = 1}^N {a_i^2} \omega _i^2} \right)^{\frac{3}{2}}}, \quad 2{\omega _1} = {\omega _2} $ | (2) |
| $ \beta_{3}=\frac{3}{2} a_{1} \omega_{1} a_{2} \omega_{2} a_{3} \omega_{3} \sin \left(\varphi_{1}+\varphi_{2}-\varphi_{3}\right) /\left(\frac{1}{2} \sum\limits_{i=1}^{N} a_{i}^{2} \omega_{i}^{2}\right)^{\frac{3}{2}}, \quad \omega_{1}+\omega_{2}=\omega_{3} $ | (3) |
由实测潮位资料调和分析结果得知,该海域潮汐不对称性的主要贡献分潮组合有3种:① K1,O1和M2;② M2和M4;③ M2,S2和MS4。根据实测临时站潮位资料,采用式(2)和(3)计算出3种组合对潮汐不对称性的贡献,如表 1所示。结果表明,红塘湾海域浅水分潮值小,与1/4潮组合的②与③其β值很小,说明其对潮位不对称性贡献小,潮汐不对称性主要来自于组合①的贡献,其值为负,代表落潮优势,与河口地区分潮对潮汐不对称性的主要贡献有所差异[9]。
| 表 1 3种分潮组合的β值 Tab.1 β of 3 combinations given by 8 stations |
图 7给出了各测站K1,O1和M2组合引起的不对称性值分布。根据此方法得出的潮汐不对称性表现为越靠近岸越大,湾内T2,T3,T4,T5四站靠近岸,其值相对大且相近,离岸远的湾外T7和T8两站,值较小,与偏度结果相似。可见,水深和离岸距离是影响该区域潮汐不对称性空间变化的重要因素。
|
图 7 K1-O1-M2组合β3值分布 Fig.7 Distribution of β3 from combination K1-O1-M2 |
不对称性在大小潮期间的变化, 在不同水域其影响主因有所差异。李谊纯认为瓯江河口潮汐不对称性的大小潮变化来自Msf分潮的影响[9];郭文云认为长江口的这种变化是受到浅水分潮与天文潮之间的相互作用共同影响形成的[14]。
红塘湾海域潮汐主要受K1,O1,M2控制,其他浅水分潮与低频分潮均不明显,推测潮汐不对称性的大小潮变化主要受到K1-O1-M2互相作用的控制。根据Hoitink提出的方法[4],将周期相近的O1,K1全日分潮合成,用其与M2半日分潮的振幅比a1/a2和相位差2φ1-φ2衡量K1-O1-M2组合引起的潮汐不对称性,其中振幅比显示不对称性大小,相位差衡量方向,其在[π/2, 3π/2]区间内时表示落潮优势,反之则为涨潮优势。
图 8为2个完整大小潮期间,振幅比与相位差随叠加潮位一同变化的曲线。可以看出在2个完整大小潮过程中,振幅比与相位差随潮位呈现出周期性变化,且一直为落潮占优。另外,大潮时,潮汐不对称性非常明显,在合成潮位由大潮向小潮过渡时快速减弱,到小潮时已经接近涨落潮均势。因此,红塘湾海域潮汐不对称性大小潮期间的变化主要受K1-O1-M2分潮互相作用的影响。

|
图 8 大小潮期间红塘站K1-O1-M1组合潮位、振幅比、相位差随时间变化过程 Fig.8 Time-dependent variations of K1-O1-M2 combination tide level, a1/a2 and phase difference at Hongtang stations during two spring-neap tide cycles |
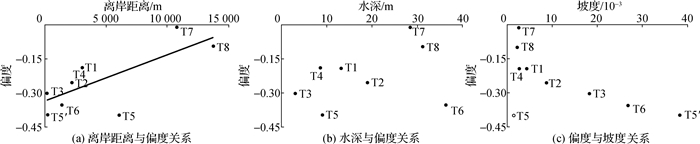
为探讨水深及离岸距离等地形要素对潮汐不对称性影响,图 9给出了偏度值随离岸距离、水深及坡度变化关系。
|
图 9 偏度值与离岸距离、水深及坡度关系 Fig.9 Relationship between γ and offshore distance, and between water depth and bottom slope |
图 9(a)为离岸距离与偏度值关系,图中T5′为用T5离西瑁洲岛距离代替其离岸距离的点。可以看出,除受西瑁洲岛影响的T5测站外,潮汐不对称性大致随着离岸距离的增加而减小,且近似线性关系。图 9(b)为水深与偏度值关系,各点比较离散,8个测站可分为3组,离岸较远T7和T8两点,离岸较近T1,T2,T4,T6四点,离岸特别近的T3和离岛特别近的T5两点。图 9(c)为偏度与坡度之间关系,潮汐偏度值随坡度增加而增加,几乎呈抛物线关系;在外海水深较大且坡度很小位置,偏度值也很小;说明离岸深海区,坡度对偏度影响极小,地形变化对潮汐不对称性几乎无影响。
分析地形要素对开敞弧形海湾潮汐不对称性影响,离岸距离和海床坡度是主要地形要素。离岸距离越远,潮汐不对称性越弱; 近岸海域,坡陡水浅增强潮汐不对称性。
4 结语(1) 开敞弧形海湾红塘湾潮汐属不正规全日潮型,天文潮占主导作用,浅水分潮作用很小。主要分潮振幅由外海向岸有增加趋势,迟角沿涨潮方向自西向东逐渐增加。
(2) 红塘湾潮汐不对称性表现为落潮主导,在短期尺度上主要受天文潮K1-O1-M2相互作用影响,随大小潮呈现周期性波动; 在长时间尺度上受K1和S2相互作用影响,有半年周期性变化; 空间上表现为由海向岸增加的规律,湾内不对称性值分布较均匀, 与湾外差异较大。
(3) 开敞弧形海湾潮汐与河口水域不同,天文潮占主导,潮汐不对称性在时间上主要受各天文潮相互作用,呈不同尺度的周期性变化;空间上与调和常数有关联,其不对称性强度受地形要素影响,主要为离岸距离和海床坡度,距岸近、坡陡、水浅时,潮汐不对称性更强。
| [1] |
AUBREY D G, SPEER P E. A study of non-linear tidal propagation in shallow inlet/estuarine systems Part I: Observations[J]. Estuarine Coastal and Shelf Science, 1985, 21(2): 185-205. DOI:10.1016/0272-7714(85)90096-4 |
| [2] |
KREEKE J V D. Tide-induced residual transport of coarse sediment; application to the EMS estuary[J]. Netherlands Journal of Sea Research, 1993, 31(3): 209-220. DOI:10.1016/0077-7579(93)90022-K |
| [3] |
FRIEDRICHS C T, AUBREY D G. Non-linear tidal distortion in shallow well-mixed estuaries: a synthesis[J]. Estuarine Coastal and Shelf Science, 1988, 27(5): 521-545. DOI:10.1016/0272-7714(88)90082-0 |
| [4] |
HOITINK A J F, HOEKSTRA P, MAREN D S V. Flow asymmetry associated with astronomical tides: implications for the residual transport of sediment[J]. Journal of Geophysical Research Oceans, 2003, 108(C10): 3315. DOI:10.1029/2002JC001539 |
| [5] |
NIDZIEKO N J. Tidal asymmetry in estuaries with mixed semidiurnal/diurnal tides[J]. Journal of Geophysical Research Oceans, 2010, 115(C8): C8006. DOI:10.1029/2009JC005864 |
| [6] |
WINTERWERP J C. Fine sediment transport by tidal asymmetry in the high-concentrated Ems River: indications for a regime shift in response to channel deepening[J]. Ocean Dynamics, 2011, 61(2-3): 203-215. DOI:10.1007/s10236-010-0332-0 |
| [7] |
MAREN D S V, GERRITSEN H. Residual flow and tidal asymmetry in the Singapore Strait, with implications for resuspension and residual transport of sediment[J]. Journal of Geophysical Research Oceans, 2012, 117(C4): C4021. |
| [8] |
林国尧, 龚文平. 海南岛莺歌海近岸的潮汐不对称与潮致余流研究[J]. 海洋学报, 2017, 39(7): 36-42. ( LIN Guoyao, GONG Wenping. Tidal asymmetry and tide-induced residual currents in the Yinggehai coast, Hainan Island[J]. Acta Oceanologica Sinica, 2017, 39(7): 36-42. DOI:10.3969/j.issn.0253-4193.2017.07.004 (in Chinese)) |
| [9] |
李谊纯, 徐群. 瓯江口内外潮汐不对称研究[J]. 水利水运工程学报, 2013(5): 61-65. ( LI Yichun, XU Qun. A study of tidal asymmetry in Oujiang estuary[J]. Hydro-Science and Engineering, 2013(5): 61-65. DOI:10.3969/j.issn.1009-640X.2013.05.009 (in Chinese)) |
| [10] |
王艳红.三亚新机场人工岛对红塘湾岸滩的影响研究[C]//中国海洋学会海洋工程分会.第十八届中国海洋(岸)工程学术讨论会论文集(下), 2017: 6. (WANG Yanhong. A study of influence of the new airport island to the shore of Hongtang bay [C]// Marine Engineering Branch of the Chinese Society for Oceanography. Proceedings of the Eighteenth China Marine (Coastal) Engineering Symposium (2), 2017: 6. (in Chinese)) http://cpfd.cnki.com.cn/Article/CPFDTOTAL-HYGC201709002034.htm
|
| [11] |
赵永印, 吕彪. 三亚红塘湾海域岸线及海床冲淤演变分析[J]. 中国水运, 2017, 17(4): 269-271. ( ZHAO Yongyin, LÜ Biao. Analysis of erosion and deposition of coastal line and bed in Hongtang region[J]. China Water Transport, 2017, 17(4): 269-271. (in Chinese)) |
| [12] |
PAWLOWICZ R. Classical tidal harmonic analysis including error estimates in MATLAB using T_TIDE[J]. Computers and Geosciences, 2002, 28(8): 929-937. DOI:10.1016/S0098-3004(02)00013-4 |
| [13] |
JEWELL S A, WALKER D J, FORTUNATO A B. Tidal asymmetry in a coastal lagoon subject to a mixed tidal regime[J]. Geomorphology, 2012, 138(1): 171-180. DOI:10.1016/j.geomorph.2011.08.032 |
| [14] |
DOODSON A T. The harmonic development of the tide-generating potential[J]. Proceedings of the Royal Society of London(SerA), 1921, 100(3): 305-329. |
| [15] |
郭文云.潮汐不对称性的时间变化特征及其对工程的响应[D].上海: 华东师范大学, 2017. (GUO Wenyun. The time-varying characteristics of tidal duration asymmetry and its response to project[D]. Shanghai: East China Normal University, 2017. (in Chinese)) http://cdmd.cnki.com.cn/Article/CDMD-10269-1017070787.htm
|
| [16] |
SONG D, WANG X H, KISS A E, et al. The contribution to tidal asymmetry by different combinations of tidal constituents[J]. Journal of Geophysical Research Oceans, 2011, 116(C12007): 338-348. |
2. Nanjing Hydraulic Research Institute, Nanjing 210029, China
 2019
2019 