2. 河海大学,江苏 南京 210098;
3. 华东勘测设计研究院有限公司,浙江 杭州 311122
裂缝问题在混凝土坝中十分普遍,故有无坝不裂之说[1]。混凝土在细观结构上是由骨料、砂浆及二者间界面过渡区组成的三相非均质准脆性复合材料[2-3]。其内部还夹杂着许多孔隙和微裂纹,这些原始缺陷在外荷载的作用下,初始损伤不断积累,应变局部化的产生导致损伤不断发展成核,最终形成宏观裂缝。宏观裂缝的失稳扩展将破坏大坝的整体结构稳定性,最终危及大坝的安全运行。混凝土坝的裂缝产生机理复杂,研究混凝土大坝裂缝扩展主要有基于宏观破坏力学的确定性理论以及考虑混凝土随机统计特性的概率统计法。考虑到混凝土大坝除受到自身结构和材料的非线性影响外,往往还受到外部随机因素的作用,单一的确定性理论或者概率论方法研究无法全面考虑其结构劣化过程的各个关键因素[4]。在大坝安全监测中,对裂缝系统的把握是基于对裂缝开度的实时监测。相关研究[5]表明,监测资料残差序列中存在混沌现象。混沌现象是指在确定性非线性系统中存在的内在随机性行为[6],在生物、物理、信息科学、气象学等诸多领域均得到了广泛应用。包腾飞[4]把裂缝作为非线性动力系统进行相空间重构研究,探索了裂缝系统混沌特征量的计算,证明了裂缝存在混沌成分。李富强[7]基于混沌动力系统的相空间重构理论,对大坝变形监测数据进行回归分析后的残差序列采用二阶Volterra滤波器建模以提高拟合精度。宋志宇等[8]将混沌优化技术应用于支持向量机模型的参数选取优化,建立了混沌优化-支持向量机的大坝位移预测模型。赵卿等[9]结合相空间重构和最小二乘支持向量机提出了适合大坝非线性变形观测数据的中长期预报的混沌-支持向量机模型。严春丽[10]采用基于Bernstein多项式的递推最小二乘自适应算法,对大坝水平位移采用多元线性回归模型拟合后的残差序列进行处理,提出了MLR-Bernstain多项式组合模型。Legendre多项式[11]因其优秀的函数逼近能力在工程领域得到了广泛运用,但对于混沌时间序列的预测算法研究较少。闫华[12]针对具有高跳速的混沌通信系统,提出了基于Legendre多项式的单步自适应预测算法,但基于Legendre多项式的预测模型研究在大坝安全监控领域尚未见到。
统计回归模型常用于大坝安全监控,但对于样本容量较少的观测时间序列建模能力较差;此外,其预测模型无法考虑残差项[13],忽略了裂缝发展演变的诸多有用信息,使得裂缝开度的预测精度不够理想。针对上述问题,本文主要研究工作如下:首先,结合Legendre多项式和递推最小二乘算法(Recursive least square, RLS)建立适合小容量样本的混凝土大坝裂缝开度实时预测模型;同时,在回归模型分离出确定性分量的基础上,采用基于Legendre多项式的RLS自适应预测模型,进行残差序列的拟合及预测分析,通过在预测模型中增加残差预测项,建立适合大容量样本的统计回归-Legendre组合模型。最后,基于陈村重力拱坝在105 m高程的裂缝开度实测数据,对模型的合理性进行计算验证。
1 Legendre多项式的基本原理这里首先简单介绍下内积空间中的正交性理论。在内积空间X中,如果某个子集D满足:∀x, y∈D且x≠y均有(x, y)=0,则子集D是正交的。同时,如果∀x∈D均满足||x||=(x, x)0.5=1,那么子集D是标准正交的。内积空间的一组线性无关的元素总能通过Gram-Schmidt正交化成为一组标准正交集。基于上述内积空间的正交性理论和Gram-Schmidt正交化处理来定义Legendre多项式。设[-1, 1]上全体连续函数的集合为C[-1, 1],采用函数加法和数乘操作创建一个线性空间,则幂函数1, x, x2, …构成该空间中的一个线性无关组,这里定义内积运算为:
| $ (h, p)=\int_{-1}^{1} h(x) p(x) \mathrm{d} x \quad \forall h, p \in \boldsymbol{C}[-1, 1] $ | (1) |
从而C[-1, 1]成为一个内积空间,在该内积空间中通过线性无关组{1, x, x2, …}的正交化得到Legendre多项式。Legendre多项式形式较多,这里采用其中一种较为简单的表达式:
| $ \boldsymbol{L}_{n}(x)=\sum\limits_{i=0}^{n}\left(\frac{(-1)^{i}(n+i) !}{(n-i) !(i !)^{2} 2^{i+1}} \times\left((1-x)^{i}+(-1)^{n}(1+x)^{i}\right)\right) $ | (2) |
Legendre多项式的正交性可由下式体现:
| $ \int_{-1}^{1} \boldsymbol{L}_{n}(x) \boldsymbol{L}_{m}(x) \mathrm{d} x=\left\{\begin{array}{cc}{0, } & {m \neq n} \\ {2 /(2 m+1), } & {m=n}\end{array}\right. $ | (3) |
Legendre多项式具有函数逼近能力,即式(2)中的一系列函数L1(x), L2(x), …的线性组合可以逼近一类广泛的函数,这也说明了Legendre多项式对非线性时间序列是具有建模能力的[12]。
式(2)中的Ln(x)是单变量的n阶Legendre多项式。为了改进模型的预测效果,这里采用如下的待定参数m元n阶Legendre多项式对混沌时间序列进行建模:
| $ \boldsymbol{L}_{n}\left(x_{1}, x_{2}, \cdots, x_{m} | \boldsymbol{W}\right)=\sum\limits_{k=1}^{m} \sum\limits_{i=0}^{n-1} w_{k, i} \boldsymbol{L}_{i}\left(x_{k}\right) $ | (4) |
式中:W=(wk, i), k=1, 2, …, m; i=0, 1, …, n-1为mn维的待定参数行向量;Li(·)为式(2)中的i阶Legendre多项式。当多项式阶数i较高时,采用式(2)计算Li(·)的计算量大,一般进行以下简化:
| $ \boldsymbol{L}_{0}(x)=1, \quad \boldsymbol{L}_{1}(x)=x $ | (5) |
此外,Legendre多项式有如下递推关系:
| $ \boldsymbol{L}_{n+1}(x)=\frac{2 n+1}{n+1} x \boldsymbol{L}_{n}(x)-\frac{n}{n+1} \boldsymbol{L}_{n-1}(x), n \geqslant 1 $ | (6) |
因此,建模过程可基于式(5)和式(6)来计算Legendre多项式的值。
2 实时预测模型的建立及算法实现递推最小二乘算法(RLS)具有快速收敛和较小的稳态误差,在信号处理领域得到了广泛运用。这里将Legendre多项式的建模方法与RLS算法相结合,建立基于Legendre多项式的RLS自适应混沌时间序列预测模型。具体建模流程如下[12]:
(1) 拟定主要参数和部分变量初值:①给定模型采用的历史测值个数m以及各测值所对应的Legendre多项式阶数n(对全部测值均采用同样阶数的Legendre多项式);②拟定RLS算法中遗忘因子α和参数β的取值;③构造1×(n·m)阶加权行向量W(i),将初始值W(0)设定为零向量。
(2) 通过RLS算法更新加权行向量W(i):①构造相应于第t+1个观测时刻的Legendre多项式的输入列向量G(t, m):
| $ \boldsymbol{G}(t, m)=[g(t), g(t-1), \cdots, g(t-m+1)]^{\mathrm{T}}, t \geqslant m $ | (7) |
其中,g(t)具有以下形式:
| $ g(i)=\left[\boldsymbol{L}_{0}\left(x_{i}\right), \cdots, \boldsymbol{L}_{t}\left(x_{i}\right), \cdots, \boldsymbol{L}_{n-1}\left(x_{i}\right)\right], i=t, t-1, \cdots, t-m+1 $ | (8) |
② 将加权行向量W(t)与输入列向量G(t, m)相乘作为t+1时刻预测值,即:
| $ x_{t+1}^{*}=\boldsymbol{W}(t) \times \boldsymbol{G}(t, m) $ | (9) |
以上算法中xi为第i时刻的裂缝开度实测值,xt+1*表示对t+1时刻的裂缝开度值的预测。
③ 利用RLS算法原理,根据t+1时刻实测值,调整相应于t+2时刻权向量W(t+1):
| $ \boldsymbol{V}(t+1)=\frac{\boldsymbol{L}(t) \boldsymbol{G}(t, m)}{\alpha+\boldsymbol{G}(t, m)^{\mathrm{T}} \boldsymbol{L}(t) \boldsymbol{G}(t, m)} $ | (10) |
| $ r_{t+1}=x_{t+1}-x_{t+1}^{*} $ | (11) |
| $ \boldsymbol{W}(t+1)=\boldsymbol{W}(t)+r_{t+1} \boldsymbol{V}(t+1)^{\mathrm{T}} $ | (12) |
| $ \boldsymbol{L}(t+1)=\frac{1}{\alpha}\left[\boldsymbol{L}(t)-\boldsymbol{V}(t+1) \boldsymbol{G}(t, m)^{\mathrm{T}} \boldsymbol{L}(t)\right] $ | (13) |
L(t)的初值L(0)为:
| $ \boldsymbol{L}(0)=(1 / \beta) \boldsymbol{I} $ | (14) |
式中:V(t+1)为(n·m)×1阶列向量;L(t+1)为(n·m)(n·m)阶方阵;I为(n·m)(n·m)阶单位矩阵。
这里对算法中涉及的参数取值问题进行说明,模型的4个重要参数包括:预测时所采用的历史采样点的个数m,各采样点所对应的Legendre多项式的阶数n,以及RLS算法中两个重要的参数α与β。由于各类非线性关系都具有独特“个性”,因此对不同混沌序列的预测建模均需具体拟定相应的参数取值,一般采用逐步试探法,具体做法如下[12]:(1)将参数α与β分别设置为0.999与0.001,这是因为从仿真结果发现,二者并非算法的敏感参数,因而可直接取为固定常数;(2)参数n与m的初值均为1,逐步增大二者取值,并在一定时间内保持不变。基于选定的误差计算方法来判断该时段的预测效果,直至满足计算误差要求即可确定合理的模型参数取值。
3 统计回归-Legendre多项式残差拟合模型对混凝土大坝裂缝开度采用统计回归模型来研究监测效应量与影响因素(水压、温度及时效等)之间的关系,其一般形式[15]可表示为:
| $ \delta(t)=\delta_{\mathrm{H}}(t)+\delta_{\mathrm{T}}(t)+\delta_{\theta}(t)+\varepsilon(t) $ | (15) |
式中:δ(t)为裂缝开度;δH(t)水压分量;δT(t)为温度分量;δθ(t)为时效分量;ε(t)为残差。采用回归分析确定δH(t),δT(t)和δθ(t)的因子的系数,则t+T时刻的预测模型[13]可表示为:
| $ \delta(t+T)=\delta_{\mathrm{H}}(t+T)+\delta_{\mathrm{r}}(t+T)+\delta_{\theta}(t+T) $ | (16) |
对比式(15)和(16)可以发现,该预测模型缺少残差项ε(t+T)。而残差项包含水压、温度以及时效分量各因子之间相互影响所导致的非线性相关性;水压和温度等环境荷载作用下,裂缝尖端应力场奇异区域混凝土产生的不可逆变形;坝体承受极端荷载或者结构劣化时导致的裂缝开度突变等[4]。所以,需要对预测模型进行修正[13]:
| $ \delta(t+T)=\delta_{\mathrm{H}}(t+T)+\delta_{\mathrm{T}}(t+T)+\delta_{\theta}(t+T)+\varepsilon(t+T) $ | (17) |
统计回归-Legendre多项式组合模型具体建模过程如下:(1)利用回归分析模型分离出各确定性分量;(2)采用基于Legendre多项式的RLS自适应预测算法对残差序列进行拟合,并在预测模型中加入残差预测项,从而构建统计回归-Legendre组合模型。
这里选取仿真试验中常用到的Logistic映射[16]来检验Legendre多项式对混沌序列的预测效果。
| $ x_{t+1}=4 x_{t}\left(1-x_{t}\right) $ | (18) |
选择归一化均方根误差(eNRMES)作为评价模型预测效果的判据:
| $ e_{\mathrm{NRMES}}=\sqrt{\frac{1}{M-1} \sum\limits_{i=1}^{M}\left(x_{t}-x_{t}^{*}\right)^{2} / \upsilon_{x}} $ | (19) |
式中:M为预测数据的个数;xt为实测值;xt*为预测值;υx为实测值的标准差。
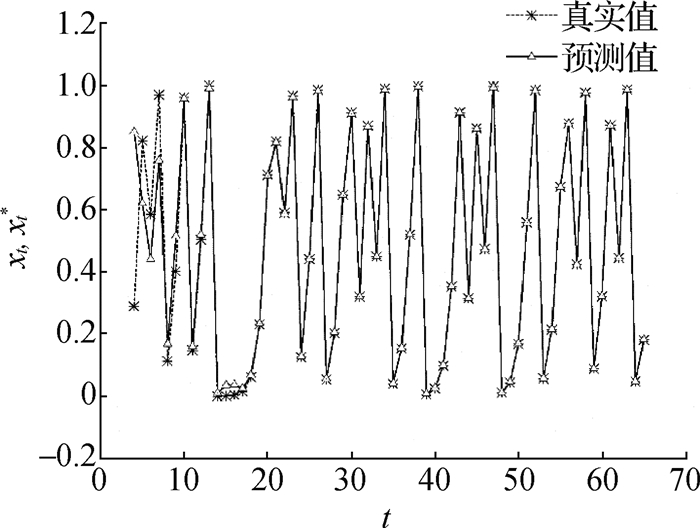
利用试算方法,给出Logistic映射产生的混沌序列所对应的参数取值:n=3,m=2,α=0.999,β=0.001。基于以上参数取值,对Logistic映射产生的混沌序列做单步预测仿真试验。为直观说明Legendre对混沌序列的预测效果,图 1给出了针对Logistic映射产生的混沌序列的单步预测仿真图像。每次仿真共取1 000个数据点,由于篇幅所限,这里仅绘制前65个点的预测仿真以说明效果,所有的数据均已归一化至[0, 1]。同时,计算得到该实时预测模型归一化均方根误差为0.076。
|
图 1 Logistic混沌序列的单步仿真图像 Fig.1 One step prediction of Logistic chaos sequence |
从图 1可以看出,由于结合了RLS这种自适应收敛算法,模型计算结果在第18个点就已经收敛,收敛速度较快,说明该算法适用于混沌时间序列的实时预测。
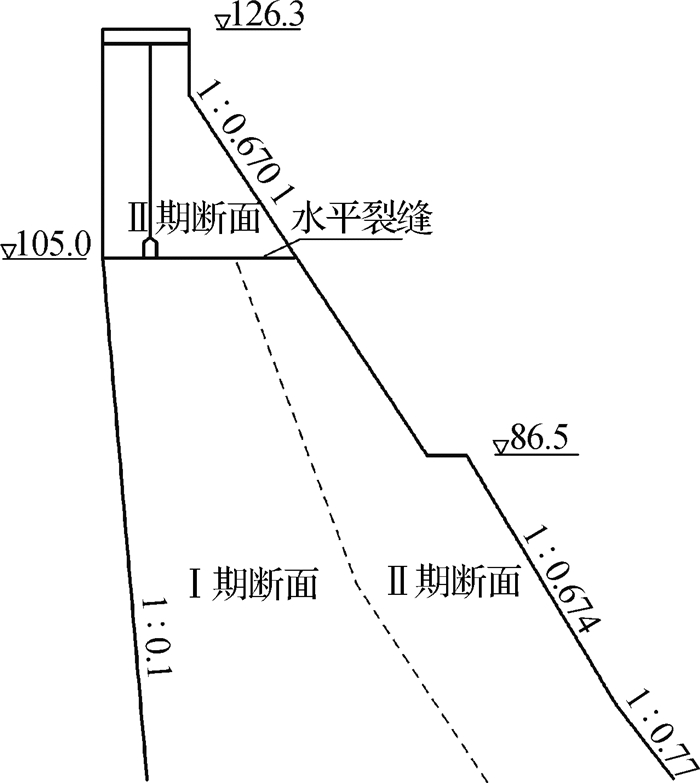
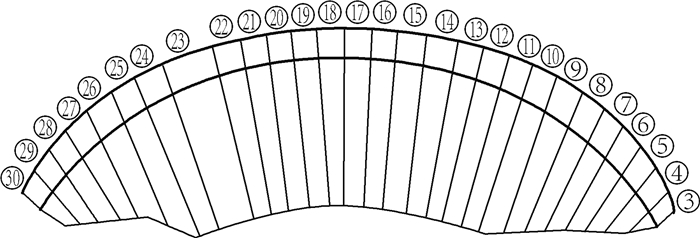
4 工程实例陈村水电站位于皖南长江支流青弋江的上游,是一座综合性中型水利水电枢纽工程。其混凝土重力拱坝的坝顶高程为126.3 m,最大坝高为76.3 m,大坝典型断面见图 2。同时,坝顶弧长419 m,自左向右共计28个坝段,编号3~30号(图 3)。工程于1958年启动,1962年完成Ⅰ期断面,1969年至1971年完成Ⅱ期断面,1978年又加高坝顶1.3 m至现在的高程126.3 m。Ⅱ期混凝土在收缩变形过程中受到Ⅰ期混凝土的约束,使得Ⅰ期混凝土的顶部,即高程105 m附近产生裂缝,以下简称105裂缝。该裂缝从5号坝段一直延伸至28号坝段,经探测裂缝深度达5 m以上,长达300多米,对坝体的整体性产生了影响。陈村大坝在105裂缝设有16只测缝计,用于及时监测裂缝开度变化,分布在8号至6号坝块。本文采用105裂缝位于18号坝段的某一选定测点的裂缝开度监测数据时间序列作为建模对象,观测时间为2004年11月20日至2013年7月18日,每3天观测1次。
|
图 2 大坝典型断面(单位:m) Fig.2 Typical section of Chencun dam (unit: m) |
|
图 3 陈村大坝各坝段编号示意 Fig.3 Numbering of each dam block |
选取2007年7月2日至2007年11月26日18号坝段目标测点的裂缝开度观测数据时间序列,该序列仅有50个裂缝开度观测值,样本容量较小,难以建立有效的统计回归模型。故采用基于Legendre多项式的RLS自适应预测算法,实时预测2007年11月29日至2008年5月30日的坝顶位移值。
预测模型具体实施步骤为:(1)采用基于Legendre多项式的RLS自适应预测算法拟合2007年7月2日至2007年11月26日的裂缝开度值;(2)采用基于Legendre多项式的RLS自适应时间序列预测算法预测2007年11月29日的裂缝开度值;(3)预测2007年12月2日裂缝开度值,由于此时已知2007年11月29日实测值,可按前述基于Legendre多项式的RLS自适应预测算法的步骤2来调整相关参数,从而得到2007年12月2日的裂缝开度值;(4)同理,可依次得到2007年12月5日至2008年5月30日的裂缝开度值。
Legendre单步预测模型的归一化均方根误差为0.048。同时,图 4为裂缝开度值的拟合与预测过程线。由图 4可知,采用基于Legendre多项式的RLS自适应预测算法的实时预测模型对裂缝开度的拟合以及实时预测结果均取得了较高的精度,模型是有效的。

|
图 4 裂缝开度拟合与预测过程线 Fig.4 Fitting and prediction results of SCMOD |
对于大容量样本的裂缝开度观测数据时间序列,这里先用统计回归模型分离出水压分量δH(t)、温度分量δT(t)和时效分量δθ(t)等确定性分量,并得出残差,再用Legendre多项式分析处理含混沌成分的残差时间序列,以提高拟合和预测精度。基于18号坝段目标测点2008年6月2日至2012年7月14日的裂缝开度监测时间序列建立统计模型回归方程。回归模型的具体建立如下:裂缝的产生和扩展与坝体应力大小有关,而应力大小与位移又有关系,所以水压对裂缝开度的影响可以参考混凝土坝位移统计模型中的水压分量因子,根据陈村重力拱坝的实际运行情况,其裂缝开度与水深H, H2, H3, H4有关;温度分量主要是坝体混凝土和基岩温度变化引起的伸缩缝的变化。陈村大坝已运行30余年,坝体已基本处于准稳定温度场变化,因此坝体混凝土温度变化可以用周期性函数等因子表示;由于裂缝受坝体混凝土徐变和缝端的塑性变形的影响,使裂缝的开合度产生不可逆变形,故需考虑时效的影响。其趋势开始剧烈,逐渐趋于稳定,所以,用线性和非线性两项表示;同时,考虑初始测值的影响,得到陈村大坝裂缝开度的回归方程如下:
| $ \begin{array}{*{20}{c}} {\delta (t) = \sum\limits_{i = 1}^4 {\left[ {{a_i}\left( {H_{\rm{u}}^i - H_{{\rm{do}}}^i} \right)} \right]} + }\\ {\sum\limits_{i = 1}^2 {\left[ {{b_{1i}}\left( {\sin \frac{{2\pi it}}{{365}} - \sin \frac{{2\pi i{t_0}}}{{365}}} \right) + {b_{2i}}\left( {\cos \frac{{2\pi it}}{{365}} - \cos \frac{{2\pi i{t_0}}}{{365}}} \right)} \right]} + } \\ {{c_1}\left( {\theta - {\theta _0}} \right) + {c_2}\left( {\ln \theta - \ln {\theta _0}} \right) + {a_0}} \end{array} $ | (20) |
式中:Hu, Hd分别为观测日、始测日所对应的上游和下游的水深值;ai为水压因子的回归系数;t为裂缝开度建模序列第1个观测日到起始观测日的累计天数;b1i, b2i为温度因子回归系数;θ为裂缝开度观测日至始测日的累计天数除以100;θ0为裂缝开度系列第1个测值日到始测日的累计天数t0除以100;c1, c2为时效因子回归系数;a0为常数项。
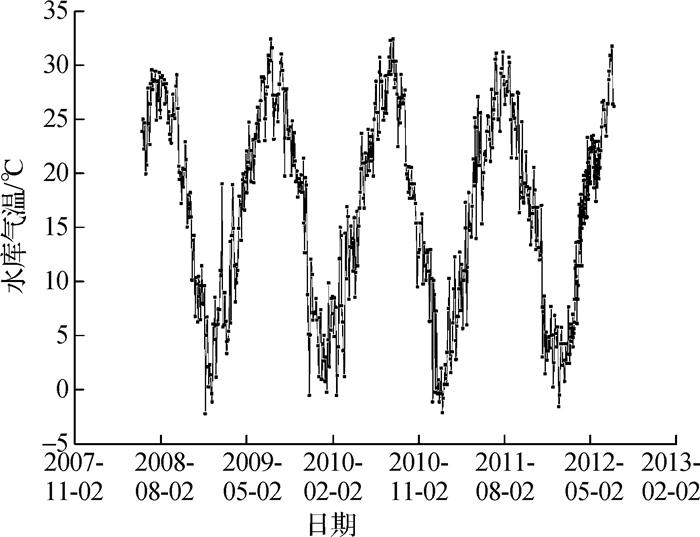
陈村混凝土重力拱坝的库水位过程线见图 5。其中,2008年6月至2010年7月的库水位整体呈逐步上升趋势,2010年7月以后至2012年7月的库水位整体略微下降;水库气温过程线见图 6,气温总体呈年周期变化,温度较低的月份为12月至次年1月,温度较高的月份为6—8月。

|
图 5 库水位过程线 Fig.5 Reservoir water level correlation line |
|
图 6 水库气温过程线 Fig.6 Reservoir temperature correlation line |
逐步回归模型各待定系数取值如表 1所示,统计回归模型的复相关系数R为0.974。同时,统计回归预测模型归一化均方根误差为0.31,可知逐步回归模型拟合效果较好。
| 表 1 回归分析成果 Tab.1 Results of regression model |
为了定量分析和评价各分量对裂缝的影响,用回归模型分离计算水压分量、温度分量和时效分量,以分析水位、温度和时效对裂缝的影响。篇幅所限,这里仅以目标测点2010年的裂缝开度测值年变幅为例,实测值1.274 mm,拟合值1.184 mm,其各分量分离情况为水压分量0.130 mm,温度分量1.006 mm,时效分量0.048 mm。温度分量、水压分量和时效分量分别占裂缝开度年变幅的84.93%,10.97%和4.10%。可见,温度变化是影响裂缝开度变化的最主要因素,其次为库水位变化的影响,时效分量影响最小。裂缝开度年均值过程线与库水位年均值过程线如图 7所示。由图 7可知,2008年至2010年库水位年均值呈逐步上升趋势,裂缝开度年均值则相应逐步下降;2010年至2011年的库水位年均值小幅下降,裂缝开度则出现增大趋势;随后,因2011年至2012年间库水位年均值上升,裂缝开度又开始减小。可以发现,库水位的变化趋势与裂缝开度变化趋势相反,原因是坝体在105 m高程以下有1: 0.1的倒悬,库水位较低时,坝体尤其是坝顶及接近坝顶的部位向上游倾斜,产生向上游的位移,导致裂缝开度增大,因此低水位工况对裂缝变形不利。

|
图 7 裂缝开度年均值过程线与库水位年均值过程线 Fig.7 Correlation line of SCMOD annual average and reservoir water level annual average |
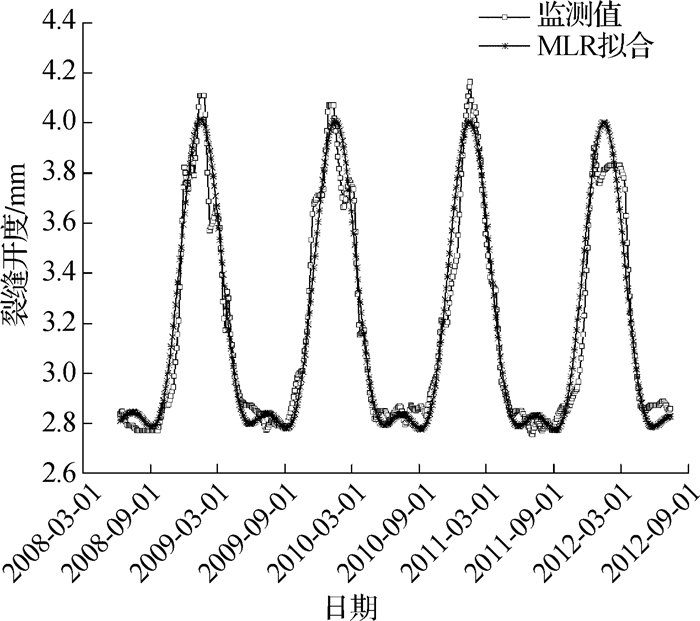
统计回归模型的裂缝开度(SCMOD)拟合过程线如图 8所示。由图 8可知,该测点的测值整体呈年周期变化,裂缝开度主要受温度变化影响,温度较低时开度较大,温度较高时开度较小,每年的裂缝开度最大值一般在温度较低的1月份或12月份出现,最小值一般在温度较高的6—8月份出现。且统计回归模型整体上能够反映测值波动规律,但极值区域的拟合精度仍有待提高。
|
图 8 裂缝开度的统计回归模型拟合过程线 Fig.8 Fitting results of SCMOD by the MLR model |
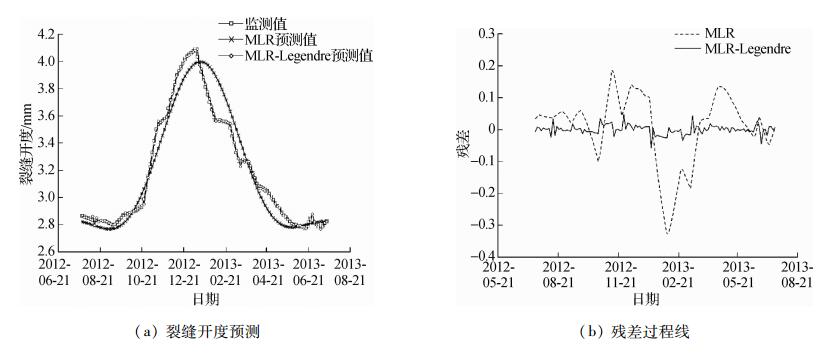
这里,利用统计回归预测模型式(17)来预测2012年7月17日至2013年7月18日的裂缝开度值。再采用基于Legendre多项式的残差时间序列预测算法修正残差序列,得到了统计回归-Legendre多项式组合模型的裂缝开度预测过程线,如图 9(a)所示。为了说明组合模型预测效果的改进,在图 9(a)中另外绘制了采用统计回归模型得到的裂缝开度预测过程线,以及裂缝开度实测过程线。可以发现,组合模型的预测精度改善明显,特别是对于突变处和极值区域的预测。
|
图 9 MLR模型和MLR-Legendre组合模型的裂缝开度预测结果和残差过程线 Fig.9 Prediction of SCMOD and residuals by MLR model and MLR-Legendre model |
图 9(b)给出了统计回归模型和统计回归-Legendre组合预测模型与实测裂缝开度之间的残差过程线。可以发现,组合模型的残差整体小于统计回归模型的残差,且突变处和极值区域的残差波动更为平顺,表现出良好的鲁棒性。组合模型的归一化均方根误差为0.032,预测精度显著提高。
5 结语混凝土坝裂缝开度监测数据时间序列存在混沌成分。本文将基于Legendre多项式的RLS自适应预测算法应用于混凝土坝的裂缝开度监测数据时间序列分析。针对统计回归模型在小样本建模时的不足以及预测模型未考虑残差项的两个问题进行改进。主要得出以下结论:
(1) 针对小样本容量的观测数据时间序列,提出了基于Legendre多项式的RLS自适应预测算法的单步预测模型。解决了统计回归模型无法对小样本容量的观测数据时间序列建立有效的统计回归模型的问题。并结合陈村重力拱坝第18号坝段的105 m高程裂缝开度测值序列进行了算例验证,结果表明单步预测模型的预测效果良好。
(2) 提出了统计回归-Legendre多项式组合模型。首先利用统计回归模型分离出确定性分量(如水压分量、温度分量、时效分量等),再采用基于Legendre多项式的RLS自适应预测算法处理残差时间序列。解决了单一统计回归模型缺少对残差序列的考虑而导致预测精度较差的问题。陈村重力拱坝第18号坝段的105 m高程裂缝开度预测分析表明,该组合模型显著提高了拟合和预测精度。
| [1] |
潘家铮. 世界上没有无裂缝的水坝[J]. 中国三峡建设, 2002, 9(4): 6-7, 47. ( PAN Jiazeng. Challenging cracks[J]. China Three Gorges Construction, 2002, 9(4): 6-7, 47. (in Chinese)) |
| [2] |
吴贞杰, 夏晓舟, 章青. 黏聚单元嵌入技术及其在混凝土细观分析模型中的应用[J]. 河海大学学报(自然科学版), 2017, 45(6): 535-542. ( WU Zhenjie, XIA Xiaozhou, ZHANG Qing. Embedding technique of cohesive element and its application in concrete mirco-level analysis model[J]. Journal of Hohai University (Natural Sciences), 2017, 45(6): 535-542. (in Chinese)) |
| [3] |
李强, 任青文, 殷亚娟. 基于数值方法的混凝土细观结构变化规律与力学性能研究[J]. 水利学报, 2015, 46(12): 1423-1433. ( LI Qiang, REN Qingwen, YIN Yajuan. Research on concrete mesoscopic structure changing law and mechanical property based on numerical methods[J]. Journal of Hydraulic Engineering, 2015, 46(12): 1423-1433. (in Chinese)) |
| [4] |
包腾飞.混凝土坝裂缝的混沌特性及分析理论和方法[D].南京: 河海大学, 2004. (BAO Tengfei. Chaotic characteristics, analysis theories and methods of cracks in concrete dams[D]. Nanjing: Hohai University, 2004. (in Chinese)) http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y578781
|
| [5] |
汪树玉, 刘国华, 杜王盖, 等. 大坝观测数据序列中的混沌现象[J]. 水利学报, 1999, 30(7): 22-27. ( WANG Shuyu, LIU Guohua, DU Wanggai, et al. Chaotic phenomenon in observation data of dam monitoring[J]. Journal of Hydraulic Engineering, 1999, 30(7): 22-27. DOI:10.3321/j.issn:0559-9350.1999.07.005 (in Chinese)) |
| [6] |
廖旎焕, 胡智宏, 马莹莹, 等. 电力系统短期负荷预测方法综述[J]. 电力系统保护与控制, 2011, 39(1): 147-152. ( LIAO Nihuan, HU Zhihong, MA Yingying, et al. Review of the short-term load forecasting methods of electric power system[J]. Power System Protection and Control, 2011, 39(1): 147-152. DOI:10.3969/j.issn.1674-3415.2011.01.028 (in Chinese)) |
| [7] |
李富强. 混沌时间序列的伏尔托拉滤波器在大坝监测分析中的应用[J]. 水利学报, 2004, 35(4): 118-122. ( LI Fuqiang. Application of Volterra filter for chaotic time series to analysis of dam monitoring data[J]. Journal of Hydraulic Engineering, 2004, 35(4): 118-122. DOI:10.3321/j.issn:0559-9350.2004.04.022 (in Chinese)) |
| [8] |
宋志宇, 李俊杰. 基于混沌优化支持向量机的大坝安全监控预测[J]. 武汉大学学报(工学版), 2007, 40(1): 53-57. ( SONG Zhiyu, LI Junjie. Research on safety monitoring forecasting model for dam based on chaos optimization support vector machine algorithm[J]. Engineering Journal of Wuhan University, 2007, 40(1): 53-57. (in Chinese)) |
| [9] |
赵卿, 李潇, 徐进军, 等. 混沌-支持向量机在大坝安全监控预测中的应用[J]. 大地测量与地球动力学, 2008, 28(2): 115-119. ( ZHAO Qing, LI Xiao, XU Jinjun, et al. Application of chaotic time series-least square support vector machine in dams' safety monitoring prediction[J]. Journal of Geodesy and Geodynamics, 2008, 28(2): 115-119. (in Chinese)) |
| [10] |
严春丽. MLR-Bernstein多项式模型在大坝监测中的应用[J]. 人民长江, 2015, 46(8): 61-70. ( YAN Chunli. Application of MLR-Bernstein polynomials model in dam safety monitoring[J]. Yangtze River, 2015, 46(8): 61-70. (in Chinese)) |
| [11] |
莫叶. 关于Legendre多项式[J]. 数学进展, 1983(4): 241-255. ( MO Ye. About the Legendre polynomial[J]. Advances in Mathematics, 1983(4): 241-255. DOI:10.11845/sxjz.1983.12.04.0241 (in Chinese)) |
| [12] |
闫华.非线性通信信号处理方法研究[D].成都: 电子科技大学, 2011. (YAN Hua. A study of methods of nonlinear communication signal processing [D]. Chengdu: University of Electronic Science and Technology of China, 2011. (in Chinese)) http://cdmd.cnki.com.cn/Article/CDMD-10614-1011240569.htm
|
| [13] |
包腾飞, 吴中如, 顾冲时. 基于统计模型与混沌理论的大坝安全监测混合预测模型[J]. 河海大学学报(自然科学版), 2003, 31(5): 534-538. ( BAO Tengfei, WU Zhongru, GU Chongshi. Statistic model and chaos theory-based hybrid forecasting model for dam safety monitoring[J]. Journal of Hohai University (Natural Sciences), 2003, 31(5): 534-538. DOI:10.3321/j.issn:1000-1980.2003.05.013 (in Chinese)) |
| [14] |
莫国瑞, 刘开第. 函数逼近论方法[M]. 北京: 科学出版社, 2003. ( MO Guorui, LIU Kaidi. Methods of approximation of functions[M]. Beijing: Science Press, 2003. (in Chinese))
|
| [15] |
顾冲时, 吴中如. 大坝与坝基安全监控理论和方法及其应用[M]. 南京: 河海大学出版社, 2006. ( GU Chongshi, WU Zhongru. Safety monitoring of dams and dam foundations-theories & methods and their application[M]. Nanjing: Hohai University Press, 2006. (in Chinese))
|
| [16] |
郭忠海, 陈永光, 李琼, 等. 基于Logistic映射的跳频序列优化[J]. 系统工程与电子技术, 2009, 31(4): 773-776. ( GUO Zhonghai, CHEN Yongguang, LI Qiong, et al. Improvement of frequency hopping sequences based on Logistic map[J]. Systems Engineering and Electronics, 2009, 31(4): 773-776. DOI:10.3321/j.issn:1001-506X.2009.04.011 (in Chinese)) |
2. Hohai University, Nanjing 210098, China;
3. Huadong Engineering Corporation Limited, Hangzhou 311122, China
 2019
2019 
