2. 南京水利科学研究院,江苏 南京 210029;
3. 黄河水利水电开发总公司,河南 济源 459017
溃坝往往伴随着难以控制的超标准洪水,不仅会对社会秩序和环境造成极大的破坏,更会造成严重的生命损失。随着我国社会经济的快速发展,溃坝可能带来的影响也会愈加严重,因此,溃坝生命损失研究越来越受到国内外水库大坝风险管理部门的重视[1-2]。在我国,对于溃坝生命损失的研究还处于起步阶段,如何较为准确地估算溃坝造成的下游生命损失是我国大坝风险管理与应急预案编制的关键技术问题[3-5]。李雷等通过分析国内外主要溃坝事件造成的生命损失情况,总结了影响生命损失的几个重要因素,评价了国外大坝溃决导致生命损失的几种估算方法[6],提出应找到适合我国实际情况的溃坝生命损失评价模型和风险人口死亡率[7],并针对沙河集水库大坝、杭州青山水库等工程实例进行溃坝生命损失估算[8-9],对我国大坝风险评价及风险管理技术的研究具有参考意义。本文应用GeoDam-BREACH中自带的SMPDAK溃坝洪水模型模拟小井沟水库下游的溃坝洪水演进过程,确定水库溃坝下游淹没范围并采用Graham法对溃坝导致的生命损失进行估算与分析。
1 工程概况小井沟水利工程位于四川省自贡市西北部荣县礼佳场越溪河上,由小井沟水库、干渠与6条支渠组成。该工程是以城市用水为主兼顾灌溉的大(2)型水利工程。防洪标准按重现期100年洪水设计,设计洪水位429.00 m,库容1.456 3亿m3;重现期2 000年洪水校核,校核洪水位430.75 m,相应库容1.659 5亿m3。小井沟水库向双溪水库输水,并与双溪水库联合调度,通过双溪水库向自贡市供水。
小井沟水库拦河大坝位于礼佳场上游小井沟峡谷河段上,地理位置在东经104°10′,北纬29°24′,坝址控制流域面积587 km2,占全流域面积的22%,河长92 km,设计流域为东北西南向的狭长形。东高西低,东为荣、威高地西缘,分水岭高程在700~800 m,西边分水岭为500~600 m[10]。
2 溃坝洪水演进计算 2.1 模拟溃坝工况溃坝是水流与坝体相互作用的一个复杂过程,一般而言,溃坝过程中的溃口最终底宽及底部最终高程与坝体的材料、施工质量及外力等因素有关。根据小井沟水利工程现有资料分析认为,可能引起小井沟水库大坝溃决的主要原因为超标准洪水引起的漫顶溃决,即大坝遇超标准水位,水位接近坝顶,上游水位持续快速增长,引起洪水漫顶,致使大坝溃决。本文假设最危险的溃坝工况为:模拟小井沟水库遇超标准水位且水位接近坝顶高程431.60 m并持续快速增长,洪水漫顶后堆石体垮塌导致面板折断,致使大坝溃决。
2.2 溃口洪水计算利用由美国联邦应急管理署(FEMA)开发的地理空间溃坝、紧急行动计划和后果风险评估(简称GeoDam-BREACH)工具包进行溃口洪水计算。主要应用的理论模型为SMPDBK模型[11],这是美国天气局NWS开发的简化计算模型。该简化模型主要是利用了依据一维不稳定流原理计算的溃坝洪水模型DAMBRK得到的洪水传播曲线来简化计算,由以下3部分组成:(1)用溃口的几何形状及水库的容积计算坝址处的洪峰流量;(2)用距离加权法和拟合技术将下游河道处理为棱柱形河道;(3)应用传播曲线来计算下游某些预报点的洪峰及其传播时间。
SMPDBK模型按以下公式计算坝址处的洪峰流量,需要的主要参数包括:溃口下切深度、最终溃口宽度以及溃决历时[12]。
| $ {Q_{{\rm{bmax}}}} = {Q_0} + 0.288{B_{\rm{r}}}{\left( {\frac{C}{{\left( {\frac{{{t_{\rm{f}}}}}{{60}} + \frac{C}{{1.811\sqrt H }}} \right.}}}\;\;\; \right)^3} $ | (1) |
| $ C=\frac{1762.3 A_{\mathrm{s}}}{B_{\mathrm{r}}} $ | (2) |
式中:Q0为溢洪道、水轮机或漫顶等非溃口流量(m3/s);Qbmax为最大溃坝流量(m3/s);H为溃口的下切深度(m);Br为溃口最终底宽(m);tf为溃坝历时(min);As为溃坝时水库水面面积。
计算得到相应溃坝工况下溃口的主要参数为:溃口最终底宽163.20 m, 底部最终高程350.00 m, 溃口下切深度81.6 m, 溃决历时26.77 min。
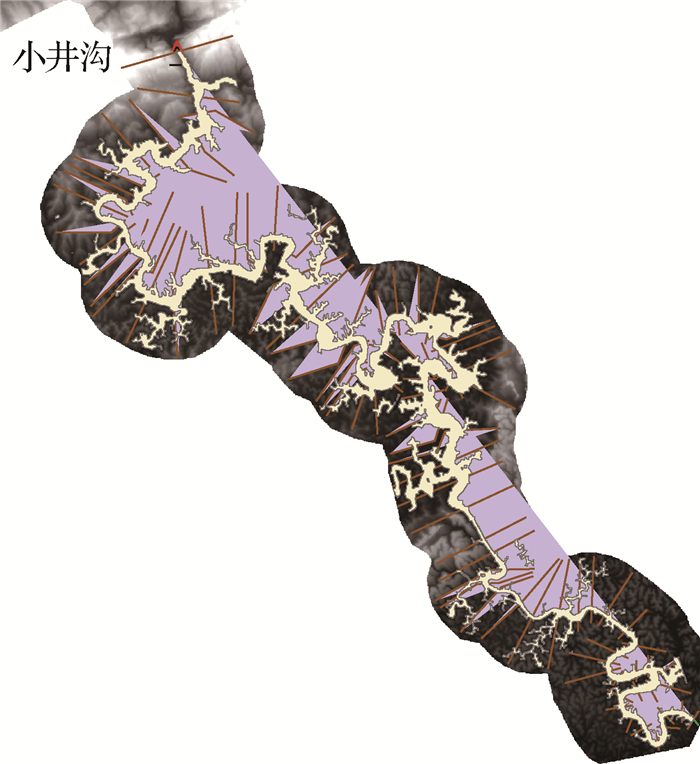
2.3 洪水演进模拟将溃口形状参数输入SMPDBK溃坝洪水模型,可计算得到小井沟水库溃坝洪水的下游演进情况以及洪水的峰值流量、流速、水深等。应用1: 10 000地形图在小井沟水库下游河道设置计算断面,模拟河道全长约为33.15 km, 即从坝址处至征远村为止,大坝下游断面划分及计算得到的溃坝洪水淹没范围见图 1。上游边界条件为简化溃坝模型计算得到的溃坝洪水流量,内边界只考虑大坝条件,支流和桥梁等其他内边界条件, 由于资料欠缺, 且在超标准洪水溃坝情况下影响小,暂不考虑。根据工程实际情况,山谷糙率取值范围0.028~0.036,河道糙率取0.026。
|
图 1 水库下游断面划分及溃坝洪水淹没范围 Fig.1 Schematic drawing of downstream cross-section and the inundated map of dam-breached flood |
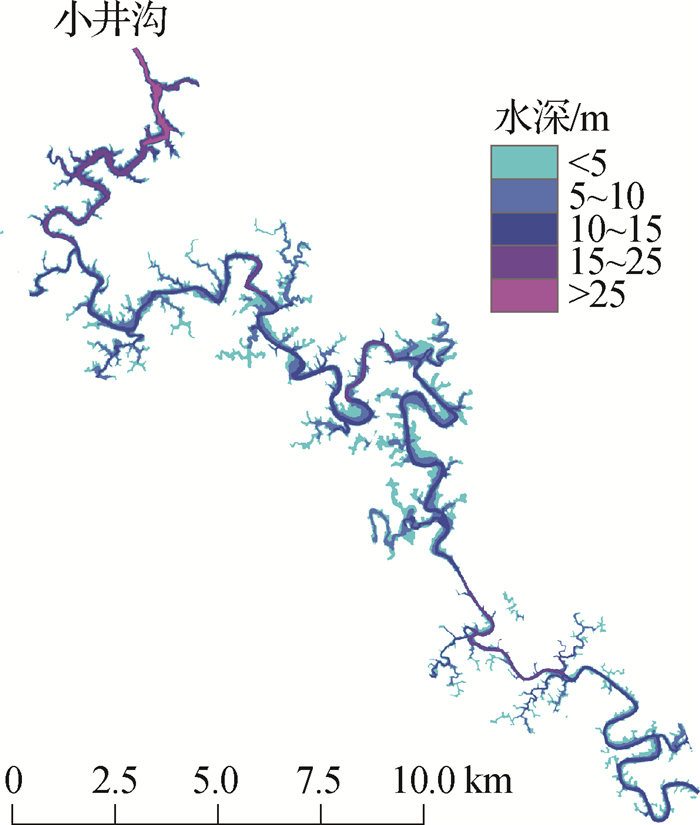
图 2为洪水淹没区域内的水深分布。由图 2可知,临近水库下游的河道段水深很大,主要原因是溃坝洪水流量大,且该区域地势存在较大落差,洪水水位抬升容易造成淹没。水库下游人员聚居区多集中在河道两岸地势平坦区域,由于河道比较曲折,加之两岸地势较低,洪水容易壅出河道,周边城镇有受淹的风险。
|
图 2 水库下游淹没区水深分布 Fig.2 Schematic drawing of depth of downstream inundated area |
国外在大量溃坝案例的研究基础上,对溃坝生命损失进行了系统研究,提出了估算溃坝生命损失的常用方法有:Dekay & McClelland法、Graham法、RESCDAM法(简化Graham法)等,李雷等分析发现采用Graham法进行生命损失估算更加简单方便且切实有效[13-14],因此本文也采用Graham法对小井沟水利工程的溃坝生命损失进行估算,评价模型如下:
| $ L_{\mathrm{ol}}=P_{\mathrm{AR}} \times f $ | (3) |
式中:生命损失Lol指受到溃坝洪水淹没而遇害的死亡人数;风险人口PAR指下泄洪水或溃坝洪水淹没范围内的人数;f为Graham法的风险人口死亡率。相关研究分析发现生命损失主要与溃坝洪水严重性、警报时间和风险人口对溃坝洪水严重性的理解程度有关[7]。
溃坝洪水严重性SD是表示洪水对下游居住区等建筑物损毁程度的参数,一般来说可用计算断面的溃坝洪水峰值流量与最大水面宽度之比q值来判定溃坝洪水严重性。q的计算式如下:
| $ q=\frac{Q_{\mathrm{df}}-Q_{2.33}}{W_{\mathrm{df}}} $ | (4) |
式中:Qdf为计算断面的溃坝峰值流量(m3/s);Q2.33为该断面的年平均流量(m3/s),一般情况下可近似取0;Wdf为溃坝洪水在该断面水面宽度的最大值(m)。
根据洪水毁坏程度及其相应的q值,溃坝洪水严重性SD定性划分为以下3个类型:①低严重性:没有建筑物从基础上被冲刷掉,大多数建筑物被淹没深度小于3 m,q≤4.6 m2/s;②中等严重性:房屋被毁坏,大部分建筑物淹没深度大于3 m,但仍然可以找到避难的地方,4.6<q≤12 m2/s;③高严重性:洪水将该地区完全冲毁,没有任何东西存在,一般可取q>12 m2/s。
警报时间WT是指溃坝警报发布后至下游群众开始撤退之间的时间,通常划分为以下3类:① WT≤15 min时,无警报,媒体或政府部门在溃坝洪水到来之前没有发布警报;② 15 min<WT≤60 min时,部分警报,警报在溃坝洪水即将到来之前发布;③ WT>60 min时,充分警报,媒体或政府能够在更早的时间发布警报。
风险人口对溃坝洪水严重性的理解程度UD是指在警报发布时,风险人口对溃坝洪水严重性是否有明确的理解和反应,对应采取的逃生必要性、措施、路径是否了解。一般来说可分为以下两种情况:①理解模糊:警报发布后公众对于即将发生或者正在发生的溃坝过程没有深刻的理解和反应能力,对溃坝引发的洪水泛滥程度和严重后果没有正确的认识。这种情况下预计达到的警报效果力度较小;②理解准确:和①情况相反,警报预计能够起到更加强而有力的作用[7]。
3.2 估算结果分析根据小井沟水库下游居民分布及人口密度,并考虑到溃坝发生在白天和夜晚的不同情况,淹没区风险人口PAR可近似等于淹没区人口与影响因子的乘积,影响因子白天取0.50,晚上取0.85[15-16]。
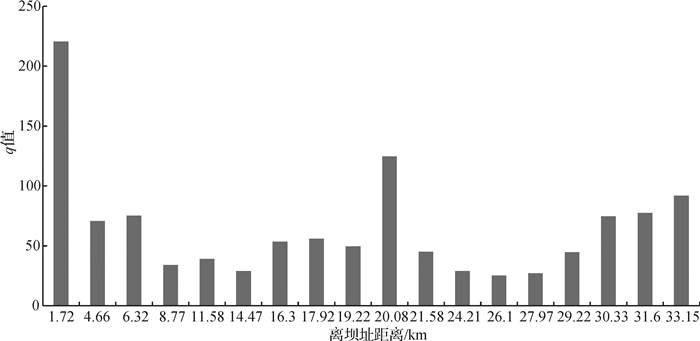
对SMPDBK溃坝洪水模型计算得到的溃坝下泄洪水演进过程进行分析,得到计算断面的溃坝峰值流量和最大水面宽度,根据q值确定溃坝洪水严重性SD,计算结果见表 1及图 3,由计算结果可知小井沟水库下游q值较高,溃坝下泄洪水对下游的影响严重。
| 表 1 溃坝洪水严重程度SD确定 Tab.1 Estimation of SD |
|
图 3 溃坝洪水严重程度SD确定 Fig.3 Estimation of SD |
假定警报时间WT为单一式的警报时间,即溃坝洪水淹没区域内的警报时间均相同。风险人口对溃坝洪水严重性的理解程度UD因警报时间的长短而变化[8],如表 2所示。根据溃坝洪水严重性、风险人口对溃坝洪水严重性的理解程度和警报时间,估算生命损失Lol,估算结果见表 2所示。
| 表 2 对溃坝洪水严重程度的理解UD和生命损失值估算 Tab.2 Estimation of UD和Lol |
本文应用GeoDam-BREACH工具包与Graham法对小井沟水库溃坝造成的生命损失进行估算,并得到以下结论:
(1) 小井沟水库下游溃坝淹没区域的风险人口死亡率较高,应当引起大坝安全管理部门和政府部门的重视,及时做好防洪应急预案工作,减少溃坝生命损失。
(2) 溃坝生命损失随着警报时间的增加而减少。当政府部门与水库管理人员及时发出溃坝警报时,生命损失较无警报减少了约1/3,而当警报时间提前1 h甚至更早发出时,生命损失已经迅速减少到管理部门可以控制的范围内,便于进行风险地区人口转移和应急救援工作。由此可见,警报时间和风险人口对溃坝洪水严重性的理解程度是生命损失的重要影响因素,应当加强水库大坝的日常巡查工作和预警系统建设,为风险地区人口的及时疏散和转移做好准备。
| [1] |
BROWN C A, GRAHAM W J. Assessing the threat to life from dam failure[J]. Jawra Journal of the American Water Resources Association, 2010, 24(6): 1303-1309. |
| [2] |
DEKAY M L, MCCLELLAND G H. Predicting loss of life in cases of dam failure and flash flood[J]. Insurance Mathematics and Economics, 2010, 13(2): 193-205. |
| [3] |
李雷, 王仁钟, 盛金保. 溃坝后果严重程度评价模型研究[J]. 安全与环境学报, 2006, 6(1): 1-4. ( LI Lei, WANG Renzhong, SHENG Jinbao. Study on evaluation models of severity degree of dam failure impact[J]. Journal of Safety and Environment, 2006, 6(1): 1-4. DOI:10.3969/j.issn.1009-6094.2006.01.001 (in Chinese)) |
| [4] |
孙玮玮, 李雷. 基于模糊数学理论的大坝风险后果综合评价[J]. 水利水运工程学报, 2010(4): 16-20. ( SUN Weiwei, LI Lei. Comprehensive hazard assessment model for consequences caused by dam failure based on fuzzy mathematics method[J]. Hydro-Science and Engineering, 2010(4): 16-20. DOI:10.3969/j.issn.1009-640X.2010.04.004 (in Chinese)) |
| [5] |
李雷, 彭雪辉, 王昭升.水库大坝溃决模式和溃坝概率分析研究[R].南京: 南京水利科学研究院, 2004. (LI Lei, PENG Xuehui, WANG Zhaosheng. Study on failure models and probability analysis of reservoir dams[R]. Nanjing: Nanjing Hydraulic Research Institute, 2004. (in Chinese))
|
| [6] |
李雷, 周克发. 大坝溃决导致的生命损失估算方法研究现状[J]. 水利水电科技进展, 2006, 26(2): 76-80. ( LI Lei, ZHOU Kefa. Methods for evaluation of life loss induced by dam failure[J]. Advances in Science and Technology of Water Resources, 2006, 26(2): 76-80. DOI:10.3880/j.issn.1006-7647.2006.02.020 (in Chinese)) |
| [7] |
周克发, 李雷, 盛金保. 我国溃坝生命损失评价模型初步研究[J]. 安全与环境学报, 2007, 7(3): 145-149. ( ZHOU Kefa, LI Lei, SHENG Jinbao. Evaluation model of loss of life due to dam breach in China[J]. Journal of Safety and Environment, 2007, 7(3): 145-149. DOI:10.3969/j.issn.1009-6094.2007.03.037 (in Chinese)) |
| [8] |
彭雪辉, 李雷, 王仁钟. 大坝风险分析及其在沙河集水库大坝的应用[J]. 水利水运工程学报, 2004(4): 21-25. ( PENG Xuehui, LI Lei, WANG Renzhong. Dam risk analysis and its application to Shaheji Dam[J]. Hydro-Science and Engineering, 2004(4): 21-25. DOI:10.3969/j.issn.1009-640X.2004.04.004 (in Chinese)) |
| [9] |
周克发, 李雷, 孙晓明. 杭州青山水库溃坝生命损失初步估算[J]. 大坝与安全, 2008(1): 9-14. ( ZHOU Kefa, LI Lei, SUN Xiaoming. Estimation of loss of life due to dam breach for Hangzhou Qingshan reservoir[J]. Dam and Safety, 2008(1): 9-14. DOI:10.3969/j.issn.1671-1092.2008.01.004 (in Chinese)) |
| [10] |
傅志敏, 袁大钊, 杨伟, 等.自贡市小井沟水利工程2017年度防洪抢险应急预案[R].南京: 河海大学, 2017. (FU Zhimin, YUAN Dazhao, YANG Wei, et al. Emergency plan for flood control and emergency work in Xiaojingou hydraulic engineering in Zigong City in 2017[R]. Nanjing: Hohai University, 2017.(in Chinese))
|
| [11] |
WETMORE J N, FREAD D L. NWS simplified dam-break flood forecasting model[R]. Maryland: National Weather Service, 1981: 1-46.
|
| [12] |
刘常铁, 陈金君, 张学东. 简化溃坝洪水预报模型(SMPDBK)的应用讨论[J]. 黑龙江水利科技, 1997(1): 67-69. ( LIU Changtie, CHEN Jinjun, ZHANG Xuedong. Discussion on the application of simplified dam-break flood forecasting model[J]. Heilongjiang Science and Technology of Water Conservancy, 1997(1): 67-69. (in Chinese)) |
| [13] |
GRAHAM W J. A procedure for estimating loss of life caused by dam failure[J]. Sedimentation and River Hydraulics, 1999, 6(5): 1-43. |
| [14] |
GRAHAM W J. A simple procedure for estimating loss of life from dam failure[R].Helsinki: RES CDAM-LOL, 2001: 1-7.
|
| [15] |
宋敬衖, 何鲜峰. 我国溃坝生命风险分析方法探讨[J]. 河海大学学报(自然科学版), 2008, 36(5): 328-633. ( SONG Jingxiang, HE Xianfeng. Discussion on analysis method for risk of life loss caused by dam failure in China[J]. Journal of Hohai University(Natural Sciences), 2008, 36(5): 328-633. (in Chinese)) |
| [16] |
董建良. 基于数字高程模型DEM的溃坝生命损失风险分析[J]. 吉林水利, 2014, 35(3): 13-16. ( DONG Jianliang. The risk analysis of dam failure caused loss of life based on digital elevation model(DEM)[J]. Jilin Water Resources, 2014, 35(3): 13-16. (in Chinese)) |
2. Nanjing Hydraulic Research Institute, Nanjing 210029, China;
3. Yellow River Water and Hydroelectric Power Development Corporation, Jiyuan 459017, China
 2019
2019 
