2. 河海大学,江苏 南京 210098
根据《2016年全国水利发展统计公报》[1],我国已建成各类水库98 460座,水库总库容8 967亿m3,承担保障国家防洪安全、供水安全、粮食安全、能源安全等重要功能。而极端气候条件会给水库带来巨大风险,水库影响区域内致灾因素与孕灾条件均复杂多变,使水库灾害的发生发展以及灾后的次生现象也复杂多变。历史上的水库大坝失事案例表明,灾害往往呈链式结构不断演化的态势,所造成的危害与影响远比单一灾害事件大且深远。如20世纪的瓦伊昂大坝报废事件[2],最初由地质灾害引发的涌浪进而造成超标准泄流以及水库报废,随着灾害的发展演进,该事件对所在区域产生极大的影响并引发各类次生衍生灾害,如交通破坏、农田破坏、火灾、社会恐慌等;我国“75.8大洪水”溃坝事件[2],淮河上游大洪水超过设计标准导致一连串大坝失事,并引发了一系列次生衍生灾害。由此可知,水库灾害作为区域性灾害并具有系统性特征,不同灾害事件间关联作用是水库灾害系统核心,也是导致水库灾害要素复杂多变的主要原因,关联作用使得灾情持续蔓延扩大,呈现出典型的形成、渗透、干涉、转化、分解、合成、耦合等特征,关联作用与灾害的危险性及风险直接联系,并呈现因果逻辑关系,在水库灾害系统中体现为复杂且动态的链式特征与效应,即水库灾变链式效应[3-8]。
1 水库灾变链灾害间因关联作用而存在动态链式逻辑关系,并在特定孕灾环境中形成具有链式结构特征的灾变链(图 1)。在水库影响区域内,水库灾变链是水库影响区域内各灾变链的集合,可分为自然灾害灾变链、事故灾难类灾变链、社会安全类灾变链和其他类灾变链[9]。依据《水库大坝安全管理应急预案编制导则》(SL/Z 720—2015)中的分类,自然灾害灾变链主要为暴雨、洪水、强震、各类地质灾害、邻近上游水库溃坝失事以及上游库区大体积漂浮物(杂物)等作为原生灾害所形成的灾变链;事故灾难类灾变链主要考虑工程质量缺陷及运行管理中的人为失误,如调度不当等;社会安全类灾变链主要考虑战争破坏、恐怖袭击、人为破坏等随机性较大的非自然灾害。
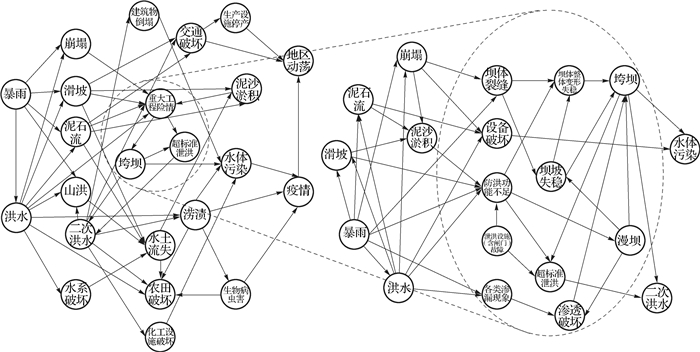
|
图 1 暴雨-洪水灾变链 Fig.1 Rainstorm-flood disaster chain |
在水库灾变系统中,一个灾害事件的发生在特定的孕灾环境下将诱发另一个灾害事件的发生,从而导致灾情的变化,该诱发过程与各灾害事件间的联系以及共现关系与环境的影响有关。灾变链风险评估模型解决的是灾害事件间诱发关系的风险(基于复杂网络理论的链式风险)问题;以灾变链中边的概率、节点的损失及边的脆弱性等3个参数综合评估灾变链风险;以“边的概率”作为灾害事件间的共现概率;以“边的脆弱性”作为后续研究的主要指标,可反映各灾害事件间的关联作用;以灾害事件的“度”代替以往常用来描述灾害损失的指标(如人员伤亡、经济损失等)。基于此,构建水库灾变链风险评估模型[10]:
| $R=\sum\limits_{i=1}^{n} P_{E_{i}} L_{V_{i}} V_{E_{i}}$ | (1) |
式中:PEi为灾变链边上所表述的概率及事件共现概率;LVi为节点i对应的灾害事件所造成的损失;VEi为灾变链边的脆弱性。上述关系可用图 2所示的逻辑关系表达。

|
图 2 灾变链逻辑关系示意 Fig.2 Schematic diagram of disaster chain logic relation |
灾变链风险评估模型主要有以下3个要点:
(1) 灾害事件的共现概率 从灾变链自身的要素(链)来讲,强调的是事件间的关联性。灾害间诱发关系导致难以预测的灾情即灾变链的核心,对灾变链进行风险评估首先要从事件的关联性入手。灾害事件的共现概率即一个灾害引起另外一个灾害的可能性。
(2) 灾害事件的损失(灾害损失) 在灾变链中灾害损失与其他灾害事件存在关联作用,其联系越大意味着该灾害事件在灾变链中影响程度较大,复杂网络理论中有许多指标可进行表达,如:联系节点“度”的概念,节点“度”可反映节点在网络中的重要程度,将灾害损失类比为网络中节点度的损失,则可考虑计算经过该点的“度”,以衡量该灾害损失,具体表达式为:F=在区域灾变链中所研究灾害事件的重要程度。由该式可知,灾害损失值F由该灾害事件关联程度以及研究区域的特性共同决定,在水库灾害系统中,若某灾害事件爆发诱发多个灾害事件,则该灾害损失将倍增,若其不诱发其他灾害则该灾害事件在区域内将会显得“不重要”,此外因研究区域而异,不同地区的水库灾害系统不一样,计算所得的损失值F也不一样。
(3) 灾变链的脆弱性 网络抗毁性是表征复杂网络的稳定性与可靠性的一个参数,指在网络中某些节点或边在受到攻击时,网络拓扑结构保持正常状态的能力,将抗毁性引入灾变链的脆弱性研究中。
2.3 水库灾变链风险评估模型的构建在构建模型并计算前需进行以下准备:水库灾变链影响因素的挖掘、水库灾变链风险评价指标的建立、灾害事件的共现概率计算、灾害链风险损失的计算及灾变链中边的脆弱性评估。
2.3.1 水库灾变链系统要素的挖掘水库灾变链的风险评估具有典型的区域特征,具体体现在灾害三要素上,为此针对水库灾变链风险评估的前期工作应当是进行水库灾变链系统的构建以及内在要素的识别。区域环境,水库影响区域内的环境即风险的来源,主要为水文气象环境、地质环境、生态环境、人文社会环境等,在调研之前需要从“孕灾”角度去收集,并做好随时记录;致灾因子主要表现的是一些影响要素的变异,如自然环境异动、人为异动、技术异动以及政治经济异动等;致灾事件即灾变链的启动事件,也是风险的开始,可细分为自然灾害事件、事故灾害事件、恐怖袭击事件以及卫生安全事件等;承灾体主要分为自然资源、人、关键基础设施以及政治经济局势,其中关键基础设施以水库大坝为核心,而政治经济局势一般当特大型水库灾害发生时考虑,而需要专门考虑,在一般的水库灾变链的分析中可不做要求。在不同灾害事件中,所组成的模块要素各有不同。水库灾变链是以水库为中心,范围选取为水库影响区域的灾变链系统,其中包含各类环境下的影响要素,主要分为自然环境类、生态环境类及社会环境类。
2.3.2 基于共现分析的水库灾害事件耦合分析模型共现分析的理论基础(邻近理论与社会学知识结构及映射)是由社会学与心理学而来的。其中,邻近理论指的是当一个事件被提及时,若其他事件与之相关,则其他事件也将在邻近发生。基于知识结构及映射原则并运用共现分析方法,挖掘文献文料中潜在内容间的关联,进而表达其中的内涵。共现理论的基本假设为:一对词语的内在关联性可在一篇文章或其他语料频繁共现中体现,且词语对的共现频率与词语间的关联程度正相关[11-12]。水库灾害事件共现分析过程:
(1) 对水库有关灾害的关键词进行数据抽取,本文采用的是数据库检索方式;
(2) 统计一定窗口内容中的有代表性词语共现频次,并构建共现矩阵或向量;
(3) 采用Salton指数法对词语关联度进行分析;
(4) 采用计算后的Salton指数作为共现概率,并构建共现概率矩阵。
灾变链的概率指的是A事件在一定情况下与B事件共同出现的概率,即A,B事件的共现概率。在灾变链风险的概率计算中,应考虑灾害事件群发性以及动态演化的特征,并基于文献资料所记载的历史灾情数据,统计过去某个事件与其他事件共现频次,并计算频率。本文运用Salton指数以计算灾害事件间共现率,其计算式如下:
| $ S_{i j}=\frac{c_{i j}}{\sqrt{c_{i} \times c_{j}}} $ | (2) |
式中:ci为词语i出现频次;cj为词语j出现频次;cij为该对词语共现频次。
2.3.3 灾变链风险损失与脆弱性的确定(1) 灾变链风险损失 参考文献[11-12]中提到的方法,将灾害链进行抽象化为一个无权有向的复杂网络,灾害事件为其节点,灾害事件间的关系为之边。灾变链上的某一灾害事件可用该节点的度来衡量,即不单考虑该事件的损失,还要考虑该事件对其他灾害事件所引起的关系。比如,i节点的度大于j节点,即i事件能够引发比j事件更多的灾害事件,则i事件所产生的损失大于j事件所带来的损失。灾变链式效应具有区域性,不同区域下的单个事件所引发的损失是不一样的,现引入区域特征参数α来调节节点的度:
| $ \alpha_{i}=\overline{F} \overline{E} $ | (3) |
式中:F 为某水库灾变系统中灾变链要素的受灾频次,
若统计周期为1,则上式可简化为:
由αi调节灾害事件在灾变链中的度,可得灾害事件i的损失为:
| $L_{i}=K_{i}^{\alpha_{i}}$ | (4) |
式中:Li为灾害事件i所引起的损失;Ki为灾害事件i在该网络体系下的度。
(2) 灾变链脆弱性 水库灾变链的边的脆弱性可表示为:
| $V_{i \in(1, k)}=B_{i} L_{i} / H_{i}$ | (5) |
式中:k为该灾变链的边数;Bi为第i条边的介数;Hi为去除第i条边后,灾变链的连通度;Li为除去第i条边后,灾变链的平均路径长度。若某条边的脆弱性越高,则该边越容易引发次生灾害,故在网络中的重要性越高;反之则越低。
2.3.4 水库灾变链链式风险度量值的计算水库灾变链中灾变链单元的风险度量值(R)=概率(P)×损失(L)×脆弱性(V):
| $R_{a b}=P L V=S_{a b} K_{b}^{\alpha_{b}} V_{a b}$ | (6) |
式中:Rab为灾害事件b的风险值,且事件b由事件a诱发;Sab为事件a,b的致灾率;Kb为事件b在网络中的度;αb为调节参数;Vab为灾变链中边ab的脆弱性。
则整条灾变链的链式风险度量值为:
| $ \begin{aligned} R=& R_{a}+R_{a b}+R_{a c}+\cdots+R_{a m}+R_{b c}+\cdots+R_{b m}+\cdots+R_{n m}=\\ & P_{a} K_{a}^{\alpha_{a}} V_{a}+P_{a b} K_{b}^{\alpha_{b}} V_{a b}+\cdots+P_{n m} K_{m}^{\alpha_{m}} V_{n m} \end{aligned} $ | (7) |
式中:m为灾害事件所涉及的区域环境要素个数;n为灾变链中灾害事件个数;P为事件概率,当P的下标为1个字符时,为该灾害事件的发生概率,当下标为2个字符时,则为2个灾害事件的共现概率,可用上文的Salton指数表示;灾害事件a作为原生灾害,则Pa=1,Va=max(Vnm)。
2.4 案例分析对位于地震高发区某水库地震灾变链(图 3)进行研究分析,该灾变链中的灾害事件为目前该区域中被关注的主要灾害。
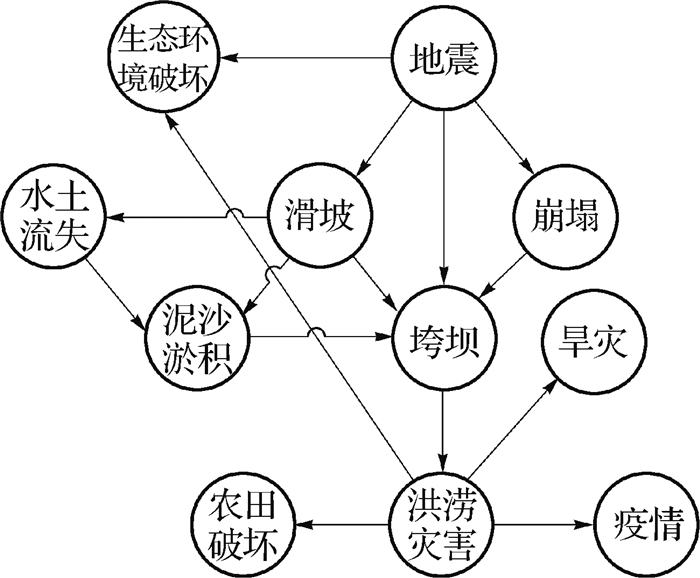
|
图 3 某水库影响区域内地震灾变链 Fig.3 Earthquake disaster chain of a reservoir |
(1) 灾变链边的概率计算 在CNKI平台对图 3中的灾害事件进行词频统计并构建共现观察值矩阵(表 1)。对共现矩阵的数据进行Salton指数运算,以求得灾害事件的关联度(表 2)。
| 表 1 检索词共现观察值矩阵 Tab.1 Retrieval term co-occurrence observation value matrix |
| 表 2 灾害事件的关联度 Tab.2 Correlation of disaster events |
(2) 灾变链节点损失计算 对历年来受灾数据进行统计(表 3),统计3周期,每周期为3年。
| 表 3 水库影响区域内受灾数据 Tab.3 Disaster data table in reservoir affected area |
对各个节点灾害进行计算,对应表 1中检索词的各个节点的损失依次为3.04,1.58,0.79,3.73,0.78,0.81,1.16,4.07,0.23,0.03和0.72。由此可知,对应的洪涝灾害、地震灾害及垮坝致灾事件的损失值较大,与实际情况相符。
(3) 灾变链边的脆弱性计算边的脆弱性计算式为:Vi∈(i, k)=BiLi/Hi,其中,Bi为第i条边的介数;Hi为除去第i条边后,灾变链的连通度;Li为除去第i条边后,灾变链的平均路径长度。因此,分别从边的介数、网络连通度以及除去边后的平均路径长度进行计算,结果如表 4所示。
| 表 4 边的脆弱性计算结果 Tab.4 Vulnerability calculation results |
由表 4可知,垮坝→洪涝灾害、泥沙淤积→垮坝、滑坡→垮坝链的脆弱性较大,在地震条件下更易引发其他灾害,在防灾减灾前应引起注意。
(4) 灾变链的链式风险度量值计算 以“地震→垮坝→洪涝灾害”链为例进行分析。地震灾害为原生灾害,即已经发生的灾害,定义概率为1(认为地震灾害无由其他灾害诱发),由于灾害事件是引起灾变链发生的原生灾害,故到地震灾害事件该边的脆弱性为该网络中的最大值,可认为存在某虚拟灾害事件引起地震灾害事件发生,它们间存在一条虚拟链。
对“地震→垮坝→洪涝灾害”(V1→V4→V8)灾变链链式风险度量值进行计算:
R(V1→V4→V8)=P1×max(Vij)×K1α1+P14× V14×K4α4+P48×V48×K8α8=1×18.98×3.04+ 0.034×10.60×3.73+0.005×18.98×4.07=59.43
表 5中链式风险度量值表征每条灾变链的链式风险大小。可见,灾变链链式风险与其广度(灾变链影响范围)及深度(灾变链长度,即连接事件数量)有关。
| 表 5 链式风险度量值排序 Tab.5 Chain-risk ranking |
水库作为重要的民生设施,其影响区域内灾害事件因各自间的关联作用导致灾情后果无可估量,故考虑灾害间关联作用进行水库灾变链风险评估并开展断链减灾工作是有待解决的问题。本文在链式风险评估及复杂网络技术的基础上,构建并运用水库灾变链风险评估模型评估灾害事件间诱发关系的风险,综合考虑了灾害事件的共现概率、灾害事件间诱发关系的脆弱性以及灾害事件移除后对网络性能的影响。
由于研究未能涵盖完全,本文对以下研究趋势进行展望:(1)灾变链中灾害事件间关联作用关系研究;(2)开展水库灾变链间相互转变的特征及机制研究;(3)基于链式风险的群发性灾害的系统性特征以及风险评估研究。
| [1] |
吴善超, 韩宇. 关于落实《国家自然科学基金"十二五"发展规划》的认识与思考[J]. 中国科学基金, 2011, 25(4): 228-232. ( WU Shanchao, HAN Yu. Thoughts on implication of the 12th five-year plan of the national natural science foundation of China[J]. China Science Foundation, 2011, 25(4): 228-232. (in Chinese)) |
| [2] |
中华人民共和国水利部. 全国水利发展统计公报(2016)[M]. 北京: 中国水利水电出版社, 2017. ( Ministry of Water Resources of the People's Republic of China. 2016 Statistic bulletin on China water activities[M]. Beijing: China Water and Power Press, 2017. (in Chinese))
|
| [3] |
张秀丽. 国内外大坝失事或水电站事故典型案例原因汇集[J]. 大坝与安全, 2015(1): 13-16. ( ZHANG Xiuli. Collection of typical cases of dam failures and accidents at hydropower stations[J]. Dam and Safety, 2015(1): 13-16. DOI:10.3969/j.issn.1671-1092.2015.01.007 (in Chinese)) |
| [4] |
DEL MONACO G, MARGOTTINI C, SPIZZICHINO D. Armonia methodology for multi-risk assessment and the harmonization of different natural risk map[M]. Rome, 2007.
|
| [5] |
HELBING D. Globally networked risks and how to respond[J]. Nature, 2013, 497(7447): 51-59. DOI:10.1038/nature12047 |
| [6] |
史培军. 四论灾害研究的理论与实践[J]. 自然灾害学报, 2005, 14(6): 1-7. ( SHI Peijun. Theory and practice on disaster system research in a fourth time[J]. Journal of Natural Disaster, 2005, 14(6): 1-7. DOI:10.3969/j.issn.1004-4574.2005.06.001 (in Chinese)) |
| [7] |
史培军. 五论灾害研究的理论与实践[J]. 自然灾害学报, 2009, 18(5): 1-9. ( SHI Peijun. Theory and practice on disaster system research in a fifth time[J]. Journal of Natural Disaster, 2009, 18(5): 1-9. DOI:10.3969/j.issn.1004-4574.2009.05.001 (in Chinese)) |
| [8] |
肖盛燮. 灾变链式理论及应用[M]. 北京: 科学出版社, 2006. ( XIAO Shengxie. Theory and application of catastrophic chain type[M]. Beijing: Science Press, 2006. (in Chinese))
|
| [9] |
MENONI S. Chains of damages and failures in a metropolitan environment: some observations on the Kobe earthquake in 1995[J]. Journal of Hazardous Materials, 2001, 86(1-3): 101-119. DOI:10.1016/S0304-3894(01)00257-6 |
| [10] |
方致远.水库灾变链式效应与断链减灾对策研究[D].南京: 南京水利科学研究院, 2018. (FANG Zhiyuan. Research on the chain effect and chain-cutting countermeasures for reservoir disaster[D]. Nanjing: Nanjing Hydraulic Research Institute, 2018. (in Chinese))
|
| [11] |
王翔.区域灾害链风险评估研究[D].大连: 大连理工大学, 2011. (WANG Xiang. Research on risk assessment of regional disaster chain[D]. Dalian: Dalian University of Technology, 2011. (in Chinese)) http://cdmd.cnki.com.cn/Article/CDMD-10141-1011108895.htm
|
| [12] |
袁宏永, 苏国锋, 陈建国, 等. 突发事件及其链式效应理论研究与应用[M]. 北京: 科学出版社, 2016. ( YUAN Hongyong, SU Guofeng, CHEN Jianguo, et al. Research and application of emergent events and their chain effect theory[M]. Beijing: Science Press, 2016. (in Chinese))
|
2. Hohai University, Nanjing 210098, China
 2019
2019 
