2. 中南冶金地质研究所,湖北宜昌 443003;
3. 中国市政工程中南设计研究总院有限公司,湖北武汉 430010
斜坡稳定性是由内在与外在因素共同控制与决定的,内在因素如斜坡岩土体抗剪强度参数随时间的不断损伤,外在因素如地震、降雨、人类工程活动等[1]。对于三峡库区内的涉水库岸斜坡,库水与降雨无疑是影响其稳定性的两个重要外在因素[2]。库水位下降时,地下水补给库水,受动水压力的作用,斜坡稳定性降低,同时大量实例表明,三峡库区92%的滑坡与降雨有关,66%的滑坡与降雨直接有关,尤其是暴雨[3],这是由于降雨入渗后不仅使坡体重度增加、基质吸力降低、产生向外的渗流力,同时还对岩土体起到软化作用[4-6],特别是当雨水顺着裂隙入渗到滑动面时,造成滑坡整体抗剪强度降低[7]。在2009年三峡库区175 m试验蓄水后,凉水井滑坡表面产生了不同程度的变形,滑坡出现了复活的迹象。因此开展降雨、库水下降条件下凉水井滑坡的变形与稳定性分析非常必要。
目前对滑坡在库水、降雨作用下的研究主要集中在两个方面。一是理论分析,推导滑坡在降雨或库水涨落作用下的渗流场变化方程,并与极限平衡理论相结合对滑坡进行稳定性评价。郑颖人等[8]基于一定的假设条件,推导了库水位下降时斜坡的浸润线表达式;时卫民等[9]建立了有地下水时边坡的安全系数求解公式,并系统分析了水对条块的力学作用;Sun等[10]分别建立了降雨与库水作用下斜坡的浸润线表达式,并以卧沙溪滑坡为例计算了其在降雨与库水耦合作用下的时效稳定性。二是数值模拟,即利用数值软件对滑坡在多种条件下的变形规律或稳定性进行研究,Hu等[11]利用Geostudio对临江Ⅱ号滑坡的稳定性进行了研究,认为库水的周期性波动可能会诱发滑坡的浅层滑动,但滑坡整体上还是处于稳定状态;倪卫达等[12]结合1个水文年内三峡库区的库水调动方案,利用Geostudio研究了临江Ⅰ号滑坡在库水位涨落条件下渗流场、位移场以及稳定性的演化规律,研究表明滑坡渗流场的变化滞后于库水的涨落,由此产生的动水压力,使得滑坡在库水下降时稳定性降低;邢小弟等[13]提出了土体抗剪强度与含水率之间的函数关系,基于Fortran语言开发了饱和-非饱和渗流有限元计算程序,并结合修正简化的Bishop法对土质边坡在降雨作用下的稳定性进行了分析。目前对凉水井滑坡的研究多集中于库水或是降雨的单独作用,如Wang等[14]利用有限元分析了库水波动时凉水井滑坡的变形与稳定性变化规律,认为库水快速下降是凉水井滑坡复活的主要原因;李伟[15]利用Abaqus研究了凉水井滑坡3个不同剖面在自重及自重加暴雨工况下的稳定性变化情况。因此,本文在前人研究的基础上,对凉水井滑坡在库水下降及联合降雨作用下的变形与稳定性进行了详细分析,定义并获取了滑坡各处的降雨响应因子与联合响应因子,从响应因子的角度揭示了凉水井滑坡变形对降雨与库水下降的响应规律,最后对凉水井滑坡在降雨以及库水作用下的稳定性进行了评价,为凉水井滑坡的治理提供了一定依据。
1 计算模型 1.1 非饱和土Van Genuchten计算模型基质吸力是研究非饱和土渗透的重要概念,可表示为:
| $ \psi=u_{\mathrm{a}}-u_{\mathrm{w}} $ | (1) |
式中:ψ为基质吸力;ua为孔隙气压力;uw为孔隙水压力。
本文模拟时采用SEEP/W模块自带的Van Genuchten经验公式来确定非饱和状态土体的渗透系数、含水量以及基质吸力。VG模型[16]公式如下
| $ \theta_{\mathrm{w}}=\left\{\begin{array}{l}{\theta_{\mathrm{r}}+\frac{\theta_{\mathrm{s}}-\theta_{\mathrm{r}}}{\left[1+(\alpha \psi)^{n}\right]^{m}}, h<0} \\ {\theta_{s}, h \geqslant 0}\end{array}\right. $ | (2) |
式中:θw为体积含水量;θs为饱和体积含水量;θr为残余体积含水量;α为与进气值有关的参数;h为压力水头;ψ为基质吸力,ψ=|h|;m和n为表示土壤水分特征曲线形状的参数,其中m=1-1/n。
同时,非饱和渗透性系数可用体积含水量表示如下[17]:
| $ k\left(\theta_{\mathrm{w}}\right)=k_{\mathrm{s}}\left(\frac{\theta_{\mathrm{w}}-\theta_{\mathrm{r}}}{\theta_{\mathrm{s}}-\theta_{\mathrm{r}}}\right)^{0.5}\left(\int_{0}^{\theta_{\mathrm{w}}} \frac{\mathrm{d} \theta_{\mathrm{w}}}{\psi} / \int_{0}^{\theta_{\mathrm{s}}} \frac{\mathrm{d} \theta_{\mathrm{w}}}{\psi}\right)^{2} $ | (3) |
联立式(2)和(3),得渗透性与基质吸力关系的解析式:
| $ k=\left\{\begin{array}{l}{\frac{k_{\mathrm{s}}\left\{1-(\alpha \psi)^{n-1}\left[1+(\alpha \psi)^{n}\right]^{-m}\right\}^{2}}{\left[\left(1+(\alpha \psi)^{n}\right]^{\frac{m}{2}}\right.}, h<0} \\ {k_{\mathrm{s}}, h \geqslant 0}\end{array}\right. $ | (4) |
式中:ks为饱和渗透系数。将式(2)与(4)称为Van Genuchten-Mualem模型。
1.2 降雨计算模型降雨量的确定按P-Ⅲ型频率分析曲线计算。经验频率采用Weibull数学期望公式计算:
| $ p_{m}=\frac{m}{n+1} \times 100 \%, m=1,2, L, n $ | (5) |
采用统计参数均值x、变差系数Cv和偏态系数Cs描述上述数值。统计参数的初值采用矩法,n年年最大暴雨系列x1,x2,…,xm,…,xn的参数计算式为:
| $ \overline{x}=\frac{1}{n} \sum\limits_{m=1}^{n} x_{m} $ | (6) |
| $ {C_{\rm{v}}} = \frac{1}{{\bar x}}\sqrt {\frac{{\sum\limits_{m = 1}^n {{{\left( {{x_m} - \bar x} \right)}^2}} }}{{n - 1}}} $ | (7) |
| $ {C_{\rm{s}}} = \frac{{n\sum\limits_{m = 1}^n {{{\left( {{x_m} - \bar x} \right)}^3}} }}{{(n - 1)(n - 2){{\bar x}^3}C_{\rm{v}}^3}} $ | (8) |
P-Ⅲ型分布函数的概率密度函数和分布函数如下:
| $ f(x) = \frac{{{\beta ^\alpha }}}{{\mathit{\Gamma }(\alpha )}}{(x - b)^{\alpha - 1}}\exp ( - \beta (x - b)),x \ge b $ | (9) |
| $ F = F\left( {x \ge {x_p}} \right)\frac{{{\beta ^\alpha }}}{{\mathit{\Gamma }(\alpha )}}\int\limits_{{x_p}}^ \propto {{{(x - b)}^{\alpha - 1}}\exp ( - \beta (x - b)){\rm{d}}x} $ | (10) |
确定经验频率点据和频率曲线线型后,改变参数,匹配曲线与经验频率点,即可得降雨值。
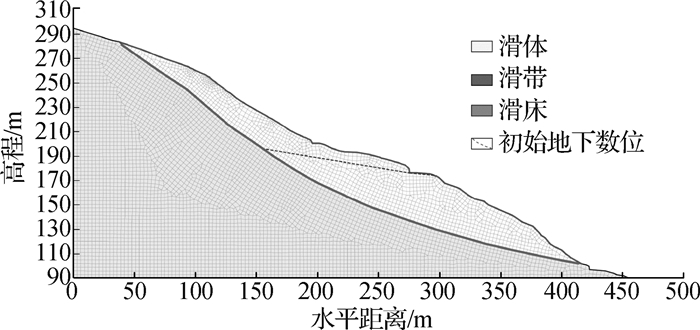
2 数值模拟计算 2.1 凉水井滑坡概况凉水井滑坡位于重庆云阳县故陵镇水让村,处于长江的右岸。从地形地貌上看,滑坡前缘较缓,后部较陡,滑坡周界平面形态呈“U”形,前缘部分在长江水位以下,长期受到江水的侵蚀作用。滑坡纵长434 m,横宽358 m,面积11.82×104 m2,平均厚度34.5 m,体积407.79×104 m3。
滑体为第四系滑坡堆积物,由粉质黏土、角砾、碎块石组成,前厚后薄。滑带为堆积层与下覆基岩接触带,厚3~5 cm,为含角砾粉质黏土。滑床由沙溪庙组(J2S)砂岩与泥岩组成,泥岩由黏土矿物组成,泥质结构;砂岩主要由石英、长石、云母等组成,细~中粒结构,且砂岩与泥岩呈不等厚的互层关系。
2.2 模型建立根据凉水井滑坡工程地质特征,选取如图 1所示的剖面作为计算剖面,并根据所示剖面进行地质建模,滑体、滑带与滑床均采用理想的线弹性模型。模型建立时采用四边形配三角形的方式进行网格剖分,共计5 631个网格节点,5 541个网格单元,如图 2所示。

|
图 1 凉水井滑坡地质剖面 Fig.1 Geological profile of Liangshuijing landslide |
|
图 2 数值计算模型 Fig.2 Numerical simulation diagram |
综合室内试验、凉水井勘查报告、数值反演及文献[14]获取滑体土、滑带土与滑床的物理力学参数(如表 1所示)。需要说明的是由于滑带土很薄,并没有做滑带的现场渗透试验,且其成分主要为含角砾粉质黏土与降水头注水试验钻孔XZK6揭露的滑体成分一致,所以其渗透系数采取钻孔XZK6的数据。初始渗流状态下的地下水位根据凉水井滑坡钻孔揭露的水位埋深情况,并参考175 m水位稳定的地下水位来确定。
| 表 1 滑坡物理力学参数 Tab.1 Physical and mechanical parameters |
在利用SEEP/W模块进行饱和-非饱和渗流分析时,Van Genuchten中所采用的参数综合现场勘查资料、数值模拟反演及文献[18]确定,含碎石粉质黏土的计算参数如下:a=24 kPa, n=1.786, m=0.439, θs=0.330 m3/m3, θr=0.030 m3/m3。
2.3 模型计算工况确定为研究凉水井滑坡在库水下降及联合降雨作用下的变形与稳定性变化规律,模拟分为2个阶段。第1阶段库水从175 m降至159 m,库水降速为0.13 m/d,历时123 d,并与凉水井滑坡的实际监测数据对应,保证模型的合理性与有效性;第2阶段是在第1阶段的基础上库水位由159 m降至145 m,即从第123天起库水位加速下降,并在库水下降期间施加降雨。根据库水降速和有无降雨分为8种工况,无降雨工况4种,库水降幅分别为0.6,0.8,1.0和1.2 m/d,历时24,18,14和12 d;降雨工况4种,即在无降雨工况基础上,在库水下降过程中加入连续的降雨,施加降雨时间为第128至130天,历时3 d。
第2阶段的降雨量通过统计1960—2013年54年间云阳县4—6月降雨资料。采用1.2节所述降雨计算模型进行曲线拟合。选取50年一遇(即频率为2%)作为计算工况,降雨强度为82.3 mm/d,计算工况如表 2所示。
| 表 2 凉水井滑坡变形与稳定性计算工况 Tab.2 Deformation and stability calculation condition of Liangshuijing landslide |
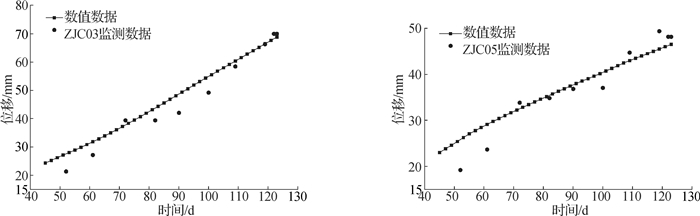
为了验证所建模型的合理性,选取凉水井滑坡中前部监测点ZJC03、中部监测点ZJC05(如图 1所示)在2010-12-18—2011-04-20期间(这一时期库水位从174.67 m降至159.29 m,历时123 d,与第1阶段的方案几乎一致)的监测位移增量与第1阶段的模型计算结果进行对比分析,由于第45天之前监测数据的位移增量为零,所以对比分析从第45天开始,分析结果如图 3所示。监测数据与数值数据具有较好的一致性,由此说明所建模型合理有效。在此基础上对凉水井滑坡在库水下降与降雨作用下的变形与稳定性进行研究。
|
图 3 对应点数值与监测位移对比 Fig.3 Displacement comparison of corresponding points between numerical and monitoring values |
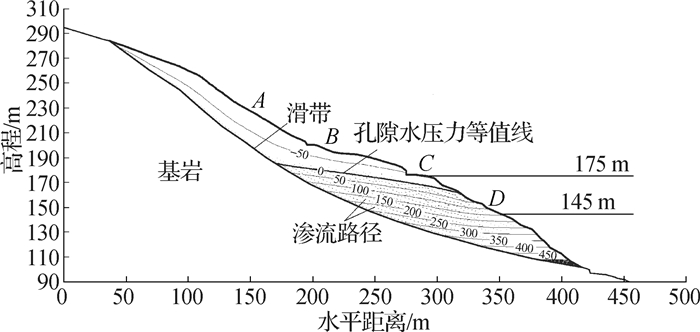
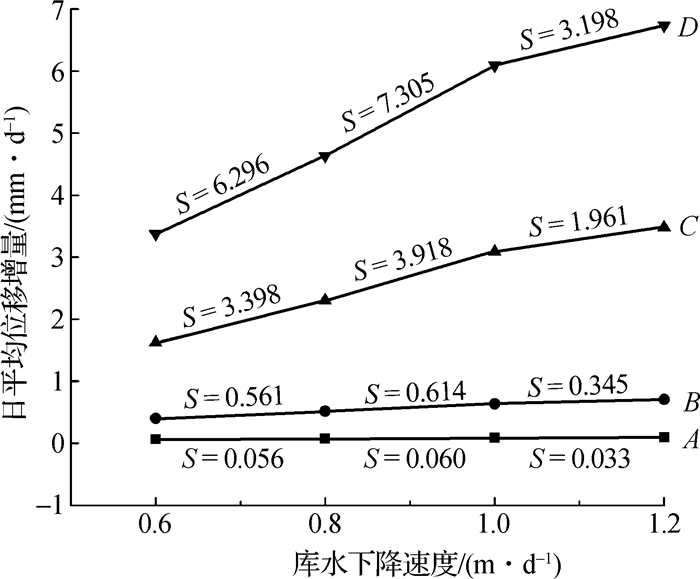
在SEEP/W模块获取滑坡渗流场的基础上,利用SIGMA/W模块对其进行变形分析。模拟过程中选取A(后缘)、B(中后部)、C(中部)和D(前缘)4个点为观测点分析边坡在8种工况下的变形发展情况,如图 4所示,不同库水下降速度时各观测点的日平均位移增量见图 5。
|
图 4 159 m水位时凉水井滑坡地下水渗流场 Fig.4 Groundwater seepage field of Liangshuijing landslide at 159 m water level |
|
图 5 各库水下降速度下观测点的日平均位移增量 Fig.5 Daily average displacement increment of observation points under different drawdown velocities |
为了分析不同库水下降速度下凉水井滑坡的变形响应规律,求解出无降雨工况下4个观测点的水平位移增量,并除以该库水下降速度下的历时,得到其日平均水平位移增量,用X表示:
| $ \overline{X}=\left(X_{145}-X_{159}\right) / T $ | (11) |
式中:X145,X159分别为某一库水降速下145 m水位与159 m水位时对应的水平位移;T为该库水降速下库水从159 m降至145 m的历时。
计算得到各观测点在不同库水下降速度下的X值,其结果如图 5所示。对于相同的库水下降速度,滑坡从A点到D点的日平均水平位移增量逐渐递增,且A点在各降速下的X值几乎都为零,说明库水下降时滑坡的变形从后缘到前缘总体上呈递增趋势,后缘变形受库水影响较小。
图 5中的S为每一段直线的斜率,反映了X随着库水下降速度的变化趋势。对于各个观测点,库水降速在0.8~1.0 m/d之间的S值均要大于0.6~0.8 m/d之间的S值,说明库水下降速度为0.6~1.0 m/d时,滑坡各点随着库水下降速度的增大变形越容易。相邻两库水降速之间的S值从A点到D点也逐渐增加,说明滑坡前缘的变形相较于后缘对库水降速的改变更加敏感。库水降速在1.0~1.2 m/d之间各点的S值相较于0.8~1.0 m/d的S值均有所减小,说明当库水降速超过1.0 m/d时,库水下降速度的增加对增加滑坡变形的效果开始减弱。
3.1.2 降雨对滑坡变形的影响为了分析降雨作用下滑坡的变形响应规律,定义降雨响应因子ηr:
| $ \eta_{\mathrm{r}}=\sum \frac{X_{\mathrm{r}}-X_{\mathrm{n}}}{X_{\mathrm{n}}} / 4 $ | (12) |
式中:Xr,Xn分别为某一库水下降速度下有降雨、无降雨工况在145 m水位时的水平位移。
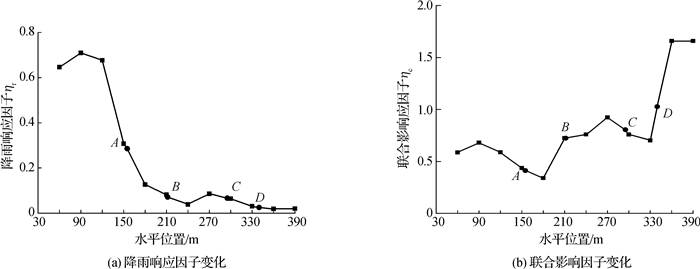
从滑坡后缘到前缘每隔30 m设置观测点并求出各点的ηr。如图 6(a)所示,降雨响应因子从后缘到前缘总体上呈递减趋势,说明滑坡后缘的变形相较于前缘对降雨更加敏感。且响应因子在水平位置120 m往后有一个陡降过程,说明降雨对滑坡变形的影响主要集中在后缘较小的一段坡体。
|
图 6 响应因子随水平位置变化 Fig.6 Changes of response factor against horizontal position |
当库水与降雨联合作用时,同样选择从滑坡后缘到前缘每隔30 m设置观测点,求出各点在联合工况下145 m水位时水平位移增量与159 m水位时水平位移比值的平均值作为联合响应因子ηc。
| $ \eta_{\mathrm{c}}=\sum \frac{X_{145}-X_{159}}{X_{159}} / 4 $ | (13) |
式中:X145,X159分别为库水与降雨联合工况下145和159 m水位时对应的水平位移。
如图 6(b)所示,联合影响因子ηc从后缘到前缘总体上呈增大趋势,说明联合作用下滑坡呈现出牵引式的变形特征。水平位置120~210 m为联合响应因子的较小区域,分析原因是库水对变形的影响从前缘到后缘总体呈递减趋势,而降雨对变形的影响总体上后缘大于前缘,联合作用下使得滑坡在中后部出现了一个局部变形“迟钝”的区域(120~210 m)。
3.2 稳定性分析在渗流场与应力场耦合分析的基础上,采用Morgenstern-Price法计算不同工况下凉水井滑坡的稳定性,计算结果如图 7和8所示。
|
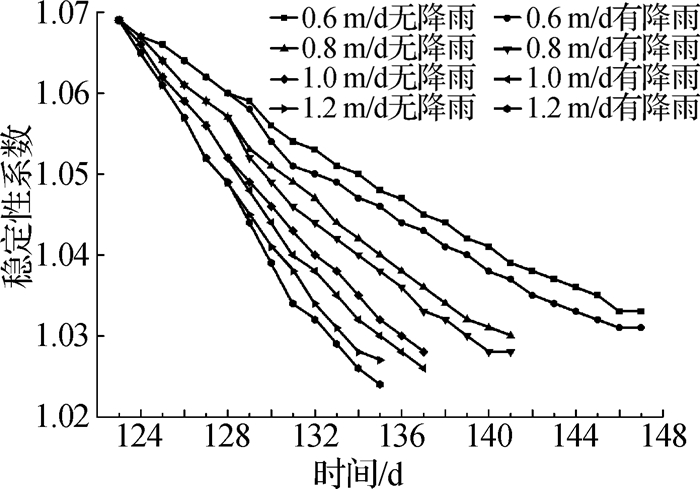
图 7 稳定性系数随时间变化曲线 Fig.7 Curves of stability coefficient against time |
|
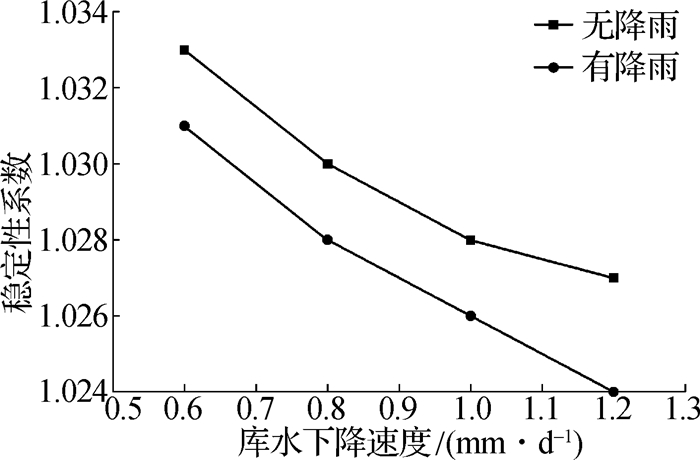
图 8 145 m水位时滑坡的稳定性系数 Fig.8 Stability coefficient of landslide at 145 m water level |
据《滑坡防治工程勘查规范》(DZ/T0218—2006),滑坡稳定系数F < 1.00时,为不稳定状态;1.00≤F < 1.05,为欠稳定状态;1.05≤F < 1.15,为基本稳定状态;F≥1.15,为稳定状态。如图 7所示,滑坡的稳定性系数随着库水位的下降逐渐降低,且库水下降速度越大稳定性系数下降越快,库水位从159 m降至145 m,稳定性系数从1.069降至1.030左右,滑坡从基本稳定状态进入欠稳定状态。根据图 8中无降雨曲线可得,145 m水位时滑坡的稳定性系数与库水降速度呈负相关关系,且曲线随着库水降速的增加逐渐变得平缓,说明当库水下降速度大于0.6 m/d时,随着库水下降速度增加稳定性系数的降幅逐渐减小,即对滑坡稳定性的弱化作用在减小。
3.2.2 降雨对滑坡稳定性的影响如图 7所示,降雨施加128 d后,滑坡的稳定性系数发生突变,且降雨3天内稳定性系数下降逐渐加剧,说明降雨会直接导致斜坡的稳定性降低。对比图 8有无降雨曲线,库水降速在0.6 m/d至1.0 m/d之间时,降雨曲线平行于无降雨曲线,两者下降趋势一致,而库水降速为1.2 m/d时,降雨对滑坡稳定性的弱化作用加强,说明库水下降速度的增加有可能会加剧降雨对滑坡的弱化作用。且145 m水位时有降雨工况滑坡的稳定性均要小于无降雨工况,但从稳定性系数降低幅度来看降雨对滑坡的弱化作用很小。
3.2.3 库水降雨联合作用下对滑坡稳定性的影响由图 7和8可知,库水下降速度为0.6 m/d时,滑坡的稳定性系数降低了0.036,明显大于降雨对滑坡稳定性的弱化作用;但当库水下降速度为1.0 m/d并联合暴雨时,滑坡稳定性系数要小于库水降速为1.2 m/d无降雨的工况,因此凉水井滑坡的稳定性主要受控于库水;但当库水下降速度大于1.0 m/d时,其稳定性对50年一遇的暴雨更加敏感。
库水降雨联合作用时,滑坡稳定性系数下降更快,对滑坡的稳定更加不利。虽然各工况下滑坡一直处于欠稳定的状态,但模拟没有考虑到岩土参数的时间损伤效应以及库水的周期性作用,因此,凉水井滑坡在库水联合暴雨的作用下很可能发生失稳破坏。
4 结语(1) 变形分析表明,凉水井滑坡的前缘变形主要受控于库水,后缘变形主要受控于降雨。坡体变形对库水下降的敏感性从后缘到前缘逐渐增大,当库水降速超过1.0 m/d时,库水下降速度增加对增加滑坡变形的作用开始减弱;降雨对边坡变形的影响主要集中在后缘较小的一段坡体。联合作用下,凉水井滑坡整体表现出牵引式的变形特征,且在滑坡中后部出现了一个变形“迟钝”的区域,其变形同时受控于降雨与库水下降,而两者在此的作用均较小。
(2) 稳定性分析表明,凉水井滑坡的稳定性主要受库水控制,滑坡的稳定性随着库水下降速度的增加而降低,但当库水下降速度大于0.6 m/d时,随着库水下降速度增加稳定性系数的降幅逐渐减小;降雨对凉水井滑坡的稳定性影响较小,但当库水下降速度大于1.0 m/d时,其稳定性对50年一遇的暴雨更加敏感。
(3) 降雨与库水联合作用时对滑坡的稳定性更加不利,联合作用并不是两者弱化作用的简单相加,库水下降速度的增加有可能会加剧降雨对滑坡的弱化作用。总体而言滑坡没有发生失稳破坏,但滑坡一直处于欠稳定的状态,且模拟没有考虑到岩土参数的时间损伤效应以及库水的周期性作用,因此在暴雨库水联合作用时凉水井滑坡很可能发生失稳破坏,进一步加强凉水井滑坡在库水长期作用下的稳定性评价非常有必要。
| [1] |
王福恒.降雨条件下山区公路边坡稳定性分析及评价[D].西安: 长安大学, 2004. (WANG Fuheng. Stability analysis and evaluation of mountain highway slope under rainfall conditions[D]. Xi'an: Chang'an University, 2004. (in Chinese)) http://cdmd.cnki.com.cn/Article/CDMD-11941-2004133287.htm
|
| [2] |
WANG J, SU A, XIANG W, et al. New data and interpretations of the shallow and deep deformation of Huangtupo No.1 riverside sliding mass during seasonal rainfall and water level fluctuation[J]. Landslides, 2016, 13(4): 795-804. DOI:10.1007/s10346-016-0712-8 |
| [3] |
王尚庆, 陆付民, 罗勉.三峡库区滑坡灾害形成机制与78防治措施[C]//全国水工岩石力学学术会议, 2010. (WANG Shangqing, LU Fumin, LUO Mian. Formation mechanism and prevention measures of landslide hazard in Three Gorges Reservoir Area[C]//National Symposium on Hydraulic Rrock Mechanics, 2010. (in Chinese))
|
| [4] |
WANG G, SASSA K. Pore-pressure generation and movement of rainfall-induced landslides: effects of grain size and fine-particle content[J]. Engineering Geology, 2003, 69(1-2): 109-125. DOI:10.1016/S0013-7952(02)00268-5 |
| [5] |
刘新荣, 张梁, 余瑜, 等. 降雨条件下酉阳大涵边坡滑动机制研究[J]. 岩土力学, 2013, 34(10): 2898-2904. ( LIU Xinrong, ZHANG Liang, YU Yu, et al. Research on sliding mechanism of Dahan slope in Youyang county under rainfall condition[J]. Rock and Soil Mechanics, 2013, 34(10): 2898-2904. (in Chinese)) |
| [6] |
王刚, 孙萍, 吴礼舟, 等. 降雨诱发浅表层黄土滑坡机理实验研究[J]. 工程地质学报, 2017(5): 1252-1263. ( WANG Gang, SUN Ping, WU Lizhou, et al. Experimental study on mechanism of shallow loess landslides induced by rainfall[J]. Journal of Engineering Geology, 2017(5): 1252-1263. (in Chinese)) |
| [7] |
BRAND E W. Some thoughts on rain-induced slope failures[C]//Proc 10th ICSMFE, 1981, 3: 373-376.
|
| [8] |
郑颖人, 唐晓松. 库水作用下的边(滑)坡稳定性分析[J]. 岩土工程学报, 2007, 29(8): 1115-1121. ( ZHENG Yingren, TANG Xiaosong. Stability analysis of slopes under drawdown condition of reservoirs[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(8): 1115-1121. DOI:10.3321/j.issn:1000-4548.2007.08.001 (in Chinese)) |
| [9] |
时卫民, 郑颖人, 唐伯明. 滑坡稳定性评价方法的探讨[J]. 岩土力学, 2003, 24(4): 545-548, 552. ( SHI Weimin, ZHENG Yingren, TANG Boming. Discussion on stability analysis method for landslides[J]. Rock and Soil Mechanics, 2003, 24(4): 545-548, 552. DOI:10.3969/j.issn.1000-7598.2003.04.011 (in Chinese)) |
| [10] |
SUN G, ZHENG H, TANG H, et al. Huangtupo landslide stability under water level fluctuations of the Three Gorges Reservoir[J]. Landslides, 2015, 1-13. |
| [11] |
HU Xinli, TANG Huiming, LI Changdong, et al. Stability of Huangtupo riverside slumping mass Ⅱ# under water level fluctuation of Three Gorges Reservoir[J]. Journal of Earth Science, 2012, 23(3): 326-334. DOI:10.1007/s12583-012-0259-0 |
| [12] |
倪卫达, 唐辉明, 胡新丽, 等. 黄土坡临江Ⅰ号崩滑体变形及稳定性演化规律研究[J]. 岩土力学, 2013, 34(10): 2961-2970. ( NI Weida, TANG Huiming, HU Xinli, et al. Research on deformation and stability evolution law of Huangtupo riverside slump-mass No.Ⅰ[J]. Rock and Soil Mechanics, 2013, 34(10): 2961-2970. (in Chinese)) |
| [13] |
邢小弟, 张磊, 谈叶飞, 等. 降雨入渗过程中土质边坡稳定性计算[J]. 水利水运工程学报, 2014(3): 98-103. ( XING Xiaodi, ZHANG Lei, TAN Yefei, et al. Calculation method for soil slope stability under the action of precipitation infiltration[J]. Hydro-Science and Engineering, 2014(3): 98-103. DOI:10.3969/j.issn.1009-640X.2014.03.015 (in Chinese)) |
| [14] |
WANG H L, XU W Y. Stability of Liangshuijing landslide under variation water levels of Three Gorges Reservoir[J]. European Journal of Environmental and Civil Engineering, 2013, 17(Suppl1): 158-177. |
| [15] |
李伟. 基于ABAQUS的凉水井滑坡稳定性分析[J]. 路基工程, 2012(4): 174-178. ( LI Wei. Analysis on landslide stability based on ABAQUS[J]. Subgrade Engineering, 2012(4): 174-178. DOI:10.3969/j.issn.1003-8825.2012.04.046 (in Chinese)) |
| [16] |
VAN GENUCHTEN M T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils[J]. Soil Science Society America, 1980, 44(5): 892-898. DOI:10.2136/sssaj1980.03615995004400050002x |
| [17] |
MUALEM Y. Hydraulic conductivity of unsaturated porous media: generalized macroscopic approach[J]. Water Resources Research, 1978, 14(2): 325-334. DOI:10.1029/WR014i002p00325 |
| [18] |
KRAHN J. Seepage modeling with SEEP/W: An engineering methodology[Z]. GEO-SLOPE International Ltd.Calgary, Alberta, Canada, 2007.
|
2. Central South Institute of Geology and Metallurgy, Yichang 443003, China;
3. Central and Southern China Municipal Engineering Design and Research Institute Co., Ltd., Wuhan 430010, China
 2019
2019 
