面板堆石坝具有良好的安全性、经济性及对地形条件强适应性等特点[1]。随着筑坝技术日渐成熟,我国已规划了多座高面板堆石坝[2-3],如茨哈峡(257.5 m)、马吉(277.5 m)等,坝高都在250~300 m。但随着面板坝高的增加,堆石体的变形性状变得更加复杂[4],而面板如果不能良好适应堆石体的变形,在水压力作用下,可能出现面板脱空或开裂的现象,因此堆石体变形和面板开裂是制约高面板堆石坝发展的主要因素。镶嵌面板坝设计理念是一种为了控制面板坝中堆石体的变形,以减小面板斜长、改善面板受力和周边缝变位为目的,在坝踵设计混凝土结构的方法。镶嵌混凝土面板堆石坝作为一种新型的坝体布置形式,国外与之相似的冰岛Karahnjukar工程,主坝是198 m高的混凝土面板堆石坝,在上游坝址处修建48 m高的混凝土趾墙,并由体积为20 000 m3的碾压混凝土结构支撑。陆希等[5-6]研究提出了一种扶壁式复式结构面板堆石坝,通过在常规混凝土面板坝坝踵处增设混凝土扶壁结构,代替深水区面板和部分堆石料,减小了面板长度,改善了超高面板堆石坝的应力变形;蔡新合等[7]为了解决200~300 m级面板堆石坝的应力变形问题,提出了一种高弹模垫座式复合坝,这种复合坝通过设置高趾墙区和低塑区,以达到降低混凝土面板应力变形的目的。通过对镶嵌混凝土面板堆石坝的分析研究,初步探讨镶嵌混凝土结构的体型对镶嵌组合坝应力变形的影响,是改善高面板堆石坝应力状态的一种新思路。
坝踵混凝土结构是镶嵌面板坝的重要组成部分。本文选择坝踵混凝土结构的高度、下游坡比及不同趾板位置作为体型控制参数,模拟镶嵌面板堆石坝的施工及蓄水过程,采用平面有限元法,对坝踵混凝土结构多种设计方案进行有限元数值分析,探究坝踵混凝土结构体型对面板应力变形的影响规律。
1 镶嵌面板坝有限元计算关键问题处理 1.1 接触面的模拟由于面板和坝踵混凝土结构的材料刚度远大于堆石料,在接触面附近会产生较大的相对位移[8],准确地模拟接触面上的受力、变形机理、应力应变关系及荷载传递过程是镶嵌面板坝应力变形特性研究的关键。本文在模拟坝踵混凝土结构与堆石体、面板与垫层、面板与趾板、面板与盖重区的接触面时,采用无厚度Goodman接触单元。Goodman接触单元考虑了接触面的非线性特性,能较好地反映接触单元的接触应力和变形过程[9]。Goodman单元的相对位移与应力的关系式[10]为:
| $ \left\{ \begin{array}{l} {\tau _{\rm{s}}}\\ {\sigma _{\rm{n}}} \end{array} \right\} = \left[ {\begin{array}{*{20}{c}} {{K_{\rm{s}}}}&0\\ 0&{{K_{\rm{n}}}} \end{array}} \right]\left\{ \begin{array}{l} {\omega _{\rm{s}}}\\ {\omega _{\rm{n}}} \end{array} \right\} $ | (1) |
式中:τs,σn分别为切向应力和法向应力;Ks,Kn为单元切向和法向刚度系数;ωs,ωn为单元两侧切向和法向的相对位移。
切向和法向刚度系数与接触单元应力变形状态有关,可表示为:
| $ {K_{\rm{s}}} = {\left( {1 - \frac{{{R_{\rm{f}}}{\tau _{\rm{s}}}}}{{{\sigma _{\rm{n}}}\tan \delta }}} \right)^2}{K_1}{\gamma _{\rm{w}}}{\left( {\frac{{{\sigma _{\rm{n}}}}}{{{P_{\rm{a}}}}}} \right)^n} $ | (2) |
| $ {K_{\rm{n}}} = {\left( {1 - \frac{{{R_{\rm{f}}}{\tau _{\rm{n}}}}}{{{\sigma _{\rm{n}}}\tan \delta }}} \right)^2}{K_2}{\gamma _{\rm{w}}}{\left( {\frac{{{\sigma _{\rm{n}}}}}{{{P_{\rm{a}}}}}} \right)^n} $ | (3) |
式中:K1,K2,Rf,n为非线性指标,由试验可以确定;σn为法向应力;δ为接触面的界面摩擦角;γw为水的重度,取值为9.8 kN/m3;Pa为大气压,取值为0.1 MPa。
1.2 扬压力的处理研究表明100 m级重力坝受到的扬压力可以达到自重20%左右[11],因此镶嵌面板坝数值计算中扬压力的影响不应忽视。如果直接将扬压力按照分布图施加在坝基面,则把扬压力当作面力处理,与实际情况不符[12]。本文对扬压力的处理采用等效模拟的方法进行,根据规范可得到扬压力的折线图,将扬压力折线图以坝基线为对称轴上翻,如图 1所示。选取对称后的扬压力分布图与坝踵混凝土结构重合的部分采用浮重度的方式处理,在结构单元上施加荷载。此方法考虑扬压力对混凝土结构的浸润上浮作用,把扬压力作为体力施加在结构上,符合实际情况。

|
图 1 扬压力等效模拟 Fig. 1 Equivalent simulation of uplift pressure |
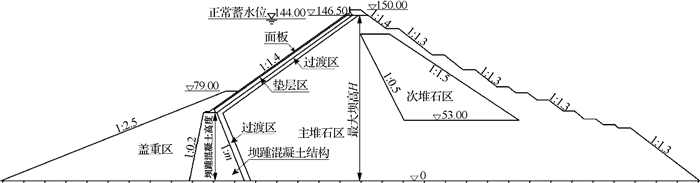
本文主要研究坝踵混凝土结构的高度、下游坡比、趾板位置对面板应力变形的影响,图 2为镶嵌混凝土面板堆石坝的标准剖面,坝体坐落于基岩上,最大坝高H=150 m。
|
图 2 镶嵌面坝堆石坝基本剖面(单位:m) Fig. 2 Basic profile of inlaid CFRD of Scheme one(unit:m) |
堆石体属于散粒体材料,其变形具有非线性、压硬性、应力路径相关性等特点,计算时堆石体本构模型采用邓肯-张E-B模型,计算参数类比采用羊曲水电站面板堆石坝筑坝材料试验成果(见表 1)。坝踵混凝土结构与堆石体、坝踵混凝土结构与盖重区、堆石体与基岩、面板与垫层、面板与盖重区、面板与趾板的接触面采用无厚度Goodman接触单元模拟,拟定的单元参数为K1=K2=4 800, n=0.56, Rf=0.74, δ=36°。坝踵混凝土结构、面板、趾板、基岩均假定为线弹性材料,面板、趾板混凝土参数取值由《混凝土结构设计规范》查得。基岩参数由同类工程类比获得,材料参数取值如下,坝踵混凝土结构ρ=2 400 kg/m3, E=2 800 MPa, 面板和趾板ρ=2 400 kg/m3, E=3 000 MPa, 基岩ρ=2 700 kg/m3, E=11 900 MPa, 所有材料的μ=0.167。
| 表 1 筑坝材料邓肯-张E-B模型参数 Tab. 1 Parameters of Duncan-Chang model (E-B) of dam materials |
坝体施工期及蓄水期荷载采用逐级加载,施工、蓄水共分22个加载级进行模拟。其中第1级模拟基岩;第2级模拟浇筑坝踵混凝土结构;第3~6级模拟混凝土结构前盖重区和结构后堆石料同步施工,填筑至坝踵混凝土结构顶部高程,并激活混凝土结构与周围堆石之间的接触;第7~18级模拟填筑坝体至坝高150 m;第19级模拟浇筑趾板;第20级模拟浇筑面板,并激活面板和趾板、面板和对应垫层之间的接触;第21级模拟填筑盖重区至坝高79 m,并激活盖重区和面板之间的接触;第22级考虑正常蓄水位以下水荷载作用在坝踵混凝土结构上游面、趾板表面和面板上,一次蓄水至正常蓄水位144 m,在混凝土结构底部施加扬压力,扬压力折减系数为0.25。计算模型见图 3。该模型在地基底面施加固定约束,上下游面按x向简支处理,坝踵混凝土结构和基岩之间按整体考虑。

|
图 3 计算模型及坐标系 Fig. 3 Finite element model and coordinate system |
根据不同的坝踵混凝土下游坡比、趾板位置、高度,设计了9个不同的计算方案,分别研究三者对面板应力变形的影响,各计算方案见表 2。
| 表 2 计算方案 Tab. 2 Calculation schemes |
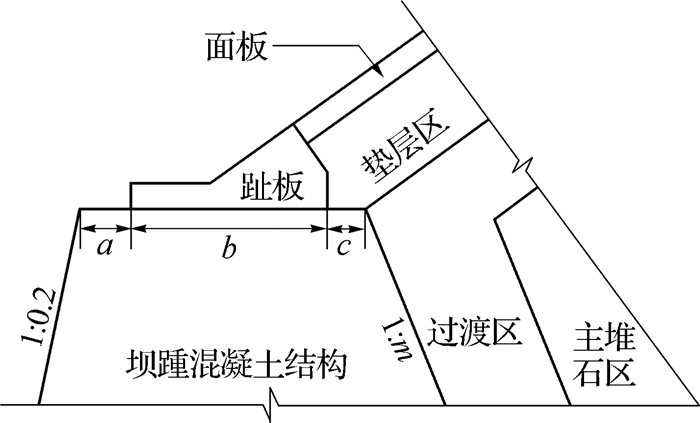
图 4为趾板相对位置示意图,图中a为趾板上游侧距离坝踵混凝土结构顶部上游边缘的距离,b为趾板长度,c为趾板下游侧距离坝踵混凝土结构顶部下游边缘的距离。
|
图 4 趾板相对位置 Fig. 4 Schematic diagram of relative position of toe plate |
坝踵混凝土结构的高度决定了面板长度,对面板应力变形有着最直接的影响,方案1、方案2和方案9设置了不同的坝踵混凝土结构高度(分别为0.27H,0.33H和0.40H),对比研究混凝土结构高度对面板应力变形的影响;坝踵混凝土结构的上下游坡比决定了其体型,改变坝踵混凝土结构的下游坡比,设计不同的计算方案(方案3、方案4和方案9),以对比研究坝踵混凝土结构下游坡比对面板应力变形的影响;趾板位于坝踵混凝土结构顶部,坝踵混凝土结构变形很小,而面板浇筑在堆石体上,蓄水过程中面板随堆石体变形而变形,面板底部与趾板间会产生较大的相对位移,导致周边缝的变位较大。以减小混凝土面板的底部变形为出发点,方案5~9通过调整趾板与坝踵混凝土结构的相对位置,达到控制周边缝变位的目的。
通过有限元计算,得出了各个方案在蓄水期面板的挠度、应力以及周边缝变位,计算结果见表 3。
| 表 3 各方案面板应力变形结果 Tab. 3 Summary of stress and deformation results of panel |
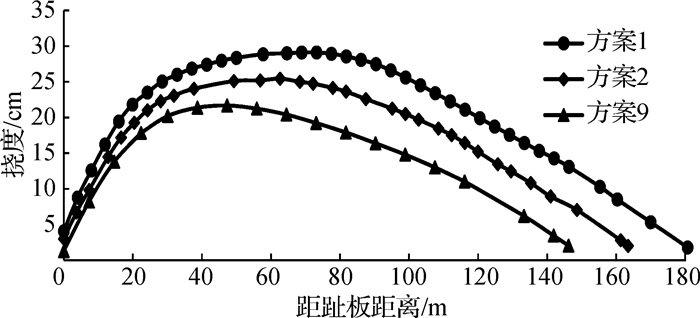
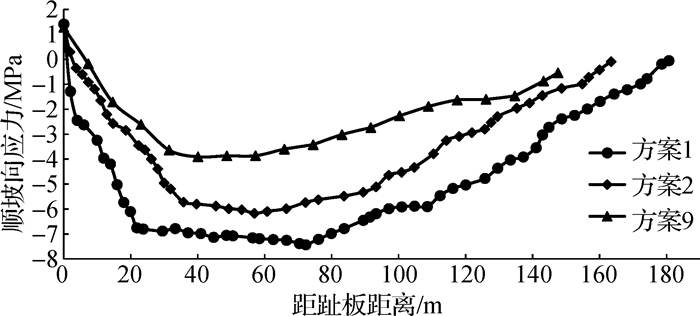
图 5和图 6分别为不同坝踵混凝土高度下面板的挠度和应力分布。
|
图 5 不同坝踵混凝土高度下面板挠度分布 Fig. 5 Deflection of face slab with different heights of concrete dam heel |
|
图 6 不同坝踵混凝土高度下面板顺坡向应力分布 Fig. 6 Stress distribution of face slab along slope with different heights of concrete dam heel |
从表 3中方案1、方案2和方案9的计算结果和图 5~6可以看出:面板挠度和顺坡向应力随坝踵混凝土结构高度的增大而减小,各方案中挠度和应力的最大值出现在大约面板斜长的1/3处。方案9中面板挠度最小,为21.68 cm;方案9中面板顺坡向应力拉应力和压应力极值最小,分别为3.91和1.28 MPa;方案1和方案9相比,周边缝张开变位从6.38 cm减小到5.02 cm,错动变位则从2.76 cm减小到2.54 cm。
坝踵混凝土结构的高度增加后,面板斜长缩短,承受的水荷载减小,面板应力变形得到改善,随着坝踵混凝土结构的高度从坝高的27%增加到坝高的40%,面板挠度最大值减小了25.5%,面板顺坡向拉压应力分别减小了9.9%和47.4%。混凝土结构高度增加后,周边缝变位也有较明显的减小,周边缝张开和错动变位分别减小了21.3%和8.0%。综合来说,增加坝踵混凝土结构高度,可有效减小面板的应力和变形。
3.2 坝踵混凝土下游坡比对面板应力变形的影响图 7和图 8分别为不同坝踵混凝土下游坡比下面板的挠度和应力分布。

|
图 7 不同下游坡比时面板挠度分布 Fig. 7 Deflection of face slab with different ratios of downstream slope |
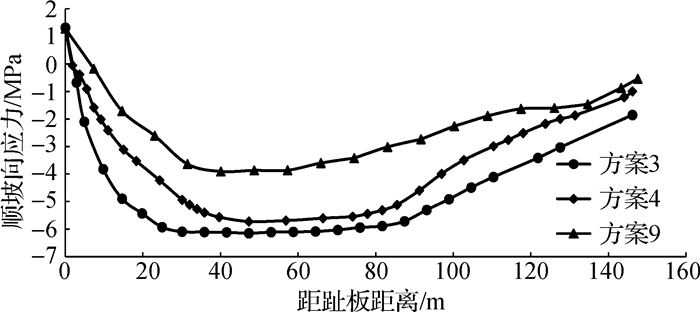
|
图 8 不同下游坡比时面板顺坡向应力分布 Fig. 8 Stress distribution of face slab along slope with different ratios of downstream slope |
对比方案3、方案4、方案9的计算结果,可以看出随着混凝土结构下游面坡度放缓,面板的挠度和应力随之减小,方案9面板最大挠度为21.68cm,较方案3减小了12.3%,面板压应力最大值为3.91 MPa,较方案3减小了36.4%,拉应力变化不大;下游坡比放缓后,周边缝张开和错动变位也略有减小,但总体上变化较小。从计算结果来看,坝踵混凝土结构的下游坡比从1:0.4变到1:0.7时,面板挠度、顺坡向拉、压应力以及周边缝变位均有逐渐变小的趋势,但数值变化较小。
3.3 趾板位置对面板应力变形的影响
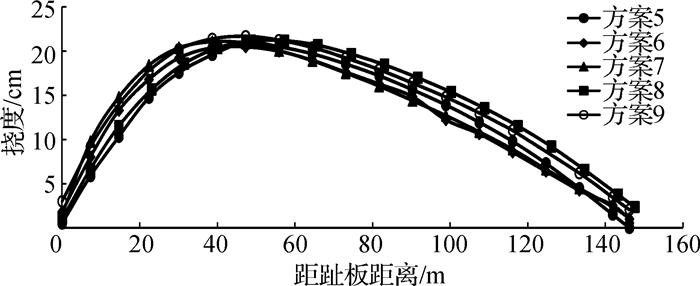
|
图 9 不同趾板位置下面板挠度分布 Fig. 9 Deflection distribution of face slab with different concrete heel positions |
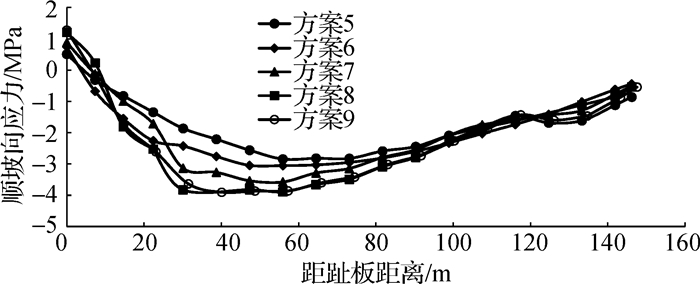
|
图 10 不同趾板位置下面板顺坡向应力分布 Fig. 10 Stress distribution of face slab along slope with different concrete heel positions |
由方案5~9的计算结果可以看出,趾板位置向上游移动时,面板的挠度和顺坡向应力有增大的趋势,从方案5到方案9,面板的挠度和顺坡向拉、压应力的最大值分别小幅变大了0.69 cm, 0.77 MPa和1.06 MPa,从图 9和10也可看出,趾板位置变化时,面板挠度和应力分布并没有明显的变化规律,这也说明趾板位置对面板挠度和应力的影响很小;周边缝变位随趾板位置向上游移动而大幅度减小,张开变位从方案5的16.03 cm减小到方案9的5.02 cm,减小了68.7%,错动变位从17.86 cm减小到2.54 cm,减小了85.8%。
趾板与坝踵混凝土结构的相对位置变化对面板的挠度和应力影响较小,但对面板底部与趾板间的相对位移影响很大。趾板位于坝踵混凝土结构顶部下游侧边缘时,面板底部有较大的位移,而趾板位置向上游布置时,坝踵混凝土结构对面板底部的“承托”作用,使面板底部位移很小,进而大幅度减小了趾板与面板间的相对位移。
4 结语本文主要研究了镶嵌混凝土面板堆石坝的坝踵混凝土结构体型对面板应力变形的影响,通过计算不同坝踵混凝土高度、下游坡比、趾板位置时的面板应力变形,得出以下结论:
(1) 坝踵混凝土结构的高度是面板应力变形的控制性因素,当混凝土结构高度从坝高的27%增加到坝高的40%时,面板的挠度、顺坡向应力都有较大程度的减小。
(2) 放缓坝踵混凝土结构的下游坡比对改善面板应力变形有正面作用,但数值变化较小。
(3) 趾板位置对面板的挠度、顺坡向应力影响很小,对周边缝变位影响巨大,当趾板位置在坝踵混凝土顶部从下游向上游移动时,面板的挠度和应力有小幅增大,而面板与趾板之间的周边缝张开变位和错动变位大幅减小了68.7%和85.8%。
综上,适当增加坝踵混凝土的高度、减小面板长度可有效改善面板的应力变形,同时,为减小趾板和面板之间的周边缝变位,可将趾板布置在偏向上游的位置。
| [1] |
党发宁, 杨超, 薛海斌, 等. 河谷形状对面板堆石坝变形特性的影响研究[J]. 水利学报, 2014, 45(4): 435-442. ( DANG Faning, YANG Chao, XUE Haibin, et al. The effect of valley topography on deformation properties of CFRD[J]. Journal of Hydraulic Engineering, 2014, 45(4): 435-442. (in Chinese)) |
| [2] |
孔宪京, 张宇, 邹德高. 高面板堆石坝面板应力分布特性及其规律[J]. 水利学报, 2013, 44(6): 631-639. ( KONG Xianjing, ZHANG Yu, ZOU Degao. Study on the stress distribution characteristics of face-slab of high concrete-face rock-fill dam[J]. Journal of Hydraulic Engineering, 2013, 44(6): 631-639. (in Chinese)) |
| [3] |
杨泽艳, 周建平, 王富强, 等. 中国混凝土面板堆石坝发展30年[J]. 水电与抽水蓄能, 2017, 3(1): 1-5, 12. ( YANG Zeyan, ZHOU Jianping, WANG Fuqiang, et al. The 30 years' development of concrete face rockfill dam in China[J]. Hydropower and Pumped Storage, 2017, 3(1): 1-5, 12. (in Chinese)) |
| [4] |
高莲士, 宋文晶, 汪召华. 高面板堆石坝变形控制的若干问题[J]. 水利学报, 2002(5): 3-8. ( GAO Lianshi, SONG Wenjing, WANG Zhaohua. Discussion on deformation control of high CFRD[J]. Journal of Hydraulic Engineering, 2002(5): 3-8. DOI:10.3321/j.issn:0559-9350.2002.05.002 (in Chinese)) |
| [5] |
陆希, 徐宏璐. 镶嵌组合坝混凝土坝体结构体型探讨[J]. 西北水电, 2014(6): 30-33, 45. ( LU Xi, XU Honglu. Study on concrete dam structural outline of embedded composite dam[J]. Northwest Hydropower, 2014(6): 30-33, 45. DOI:10.3969/j.issn.1006-2610.2014.06.008 (in Chinese)) |
| [6] |
陆希, 姚栓喜, 周恒, 等.一种扶壁式复式结构面板堆石坝: CN206495188U[P].2017-09-15. (LU Xi, YAO Shuanxi, ZHOU Heng, et al. Abutting wall type composite structure concrete faced rockfill dam: CN206495188U[P].2017-09-15. (in Chinese))
|
| [7] |
蔡新合, 姚栓喜, 雷艳, 等.一种高弹模垫座式复合坝: CN104120686A[P]. 2014. (CAI Xinhe, YAO Shuanxi, LEI Yan, et al. A kind of high elastic modulus cushion composite dam: CN104120686A[P]. 2014. (in Chinese))
|
| [8] |
李昌彩. 水布垭面板堆石坝前期关键技术研究[M]. 北京: 中国水利水电出版社, 2005. ( LI Changcai. Research on the key technology of Shuibuya CFRD[M]. Beijing: China Water Power Press, 2005. (in Chinese))
|
| [9] |
李守德, 俞洪良. Goodman接触面单元的修正与探讨[J]. 岩石力学与工程学报, 2004, 23(15): 2628-2631. ( LI Shoude, YU Hongliang. Modification of Goodman interface element[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(15): 2628-2631. DOI:10.3321/j.issn:1000-6915.2004.15.027 (in Chinese)) |
| [10] |
熊欢, 王清友, 高希章, 等. 沙湾水电站一期围堰塑性混凝土防渗墙应力变形分析[J]. 水力发电学报, 2010, 29(2): 197-203, 189. ( XIONG Huan, WANG Qingyou, GAO Xizhang, et al. Stress deformation analysis of plastic concrete cutoff wall for the first stage cofferdam of Shawan hydropower station[J]. Journal of Hydroelectric Engineering, 2010, 29(2): 197-203, 189. (in Chinese)) |
| [11] |
李征, 张林, 陈媛, 等. 不同地质条件下重力坝扬压力等效模拟方法分析[J]. 四川大学学报(工程科学版), 2016, 48(增刊2): 93-99. ( LI Zheng, ZHANG Lin, CHEN Yuan, et al. Study on the equivalent method for simulating the uplift pressure of gravity dam based on different foundations[J]. Journal of Sichuan University(Engineering Science Edition), 2016, 48(Suppl2): 93-99. (in Chinese)) |
| [12] |
李珍.重力坝深层抗滑稳定问题的非线性有限元法研究[D].南京: 河海大学, 2007. (LI Zhen. Analysis of deep anti-slide of gravity dam based on nonlinear finite element method[D]. Nanjing: Hohai University, 2007. (in Chinese))
|
 2019
2019 