2. 水利部土石坝破坏机理与防控技术重点实验室 江苏 南京 210029;
3. 南京市江宁区水务局,江苏 南京 211112
我国土石坝工程应力变形计算中普遍采用邓肯双曲线非线性弹性模型和“南水”双屈服面弹塑性本构模型模拟筑坝粗粒料的应力变形特性,两个模型均采用Mohr-Coulomb强度准则,其切线模量表达式[1-2]为
| $ {E_{\rm{t}}} = {\left( {1 - {R_{\rm{f}}}{S_{\rm{L}}}} \right)^2} \cdot k \cdot {p_{\rm{a}}} \cdot {\left( {{\sigma _3}/{p_{\rm{a}}}} \right)^n} $ | (1) |
式中:Et为切线模量;Rf为破坏比参数;k和n分别为初始模量基数及其指数,即Ei=k·pa·(σ3/pa)n;pa为大气压力;σ3和SL分别为小主应力和应力水平。
上述模型得到广泛应用的主要原因之一是参数确定的便利性,其基本假定是偏应力(σ1-σ3)与轴向应变(ε1)之间的双曲线关系[1],即
| $ {\sigma _1} - {\sigma _3} = {\varepsilon _1}/\left( {a + b{\varepsilon _1}} \right) $ | (2) |
式中:a是初始模量Ei的倒数,即a=1/Ei;b是偏应力渐进值(σ1-σ3)ult的倒数,即b=1/(σ1-σ3)ult。在整理应力变形参数时,通常将式(2)改写为以下线性形式:
| $ {\varepsilon _1}/\left( {{\sigma _1} - {\sigma _3}} \right) = a + b{\varepsilon _1} $ | (3) |
式中:a和b是试验数据在ε1-ε1/(σ1-σ3)平面上最佳拟合直线在纵坐标上的截距及其斜率。
三轴压缩试验中,粗颗粒料应力应变关系在低应力水平和高应力水平时常常偏离双曲线假定,给模型参数确定带来了很大的不确定性[3]。我国《土工试验规程》(SL 237—1999)建议,取应力水平0.70和0.95时两点的连线确定式(3)中a和b值。由于土石坝内应力水平通常在0.75以下[3],且常规三轴试验加载初期结果受到装样等因素影响具有较大的离散型,刘大康等建议根据应力水平为0.50和0.75时的试验数据确定初始模量和偏应力渐进值[3]。上述参数确定方法的本质都是根据高应力水平时的试验结果,通过外延分析,确定初始切线模量Ei,因此参数确定中的不确定性始终是存在的。
初始切线模量的实质是小应变条件下的应力应变特性,较为有效的测定方法是开展小应变试验,如共振柱试验[4]、弯曲元试验[5-6]以及基于局部应变测量的三轴试验[7-8]等,这些室内试验技术在黏土和砂土小应变剪切模量测试中运用较为广泛,但在粗颗粒料中使用较少。此外,共振柱和弯曲元试验测得的动剪切模量可能高估静力加载时的初始模量[8-9],故不适用于土石坝填筑、蓄水等静力加载过程模拟。我国已广泛采用试样直径30 cm的大型三轴试验确定粗颗粒料的强度变形参数,探讨基于常规三轴压缩试验的切线模量表达式及其参数确定方法具有实际意义。
本文以水布垭面板堆石坝和糯扎渡心墙堆石坝的实测沉降以及有限元计算结果为例,研究了土石坝的应变量级与应力水平。提出了一个新的切线模量表达式与参数确定方法,能够更好地模拟粗颗粒料的轴向应力应变特性,且参数确定的不确定性大为降低,为提高土石坝应力变形预测的可靠性奠定了基础。
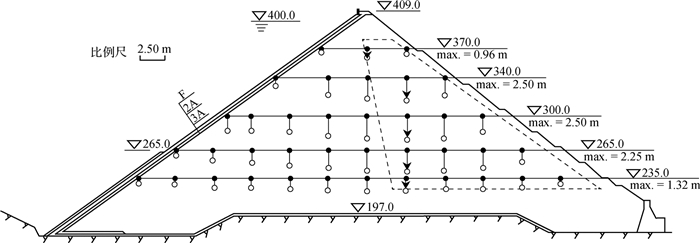
1 高土石坝的应变量级与应力水平 1.1 高面板堆石坝图 1是我国清江水布垭面板堆石坝(最大坝高233 m)最大断面沉降监测结果,各测点的原始位置(黑点表示)与沉降后的位置(白点表示)之间的距离表示沉降值的大小。该监测断面共布设5层沉降仪,各监测高程及其最大沉降量亦示于图中。可以推断,高程越低的部位填筑越早,其应变量值越大。以高程235 m的监测层为例,最大沉降量为1.32 m,位于坝轴线附近,该沉降是由高程235 m以上坝体填筑、高程197~235 m之间堆石体压缩引起的。因此,坝轴线处235 m以下堆石体平均竖向应变为1.32 m/38 m≈3.5%。
|
图 1 水布垭面板坝最大断面沉降监测结果(2010-04-22)(单位:m) Fig. 1 Settlement monitoring data at the maximum section in Shuibuya CFRD (2010-04-22)(unit: m) |
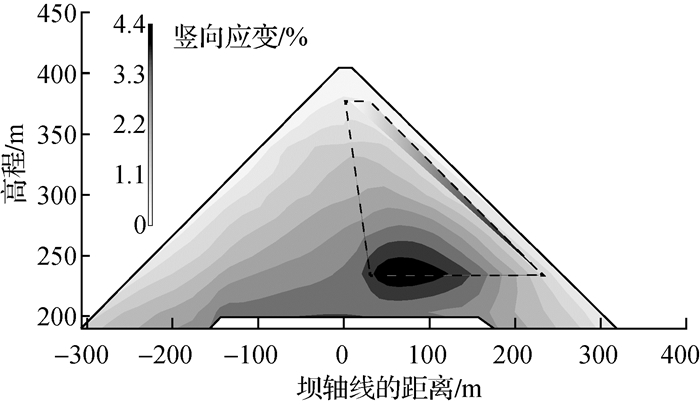
图 2是三维有限元计算得到的最大断面竖向应变分布云图,其中计算模型为“南水”双屈服面模型,参数由变形监测资料反演分析得到[10]。满蓄时,该断面的最大竖向应变约为4.4%,位于主、次堆石的水平向交界面附近。根据反演分析结果,主、次堆石的模量基数比约为1.65[10],因此,可以较明显地看出,相同高程处,次堆石区的竖向应变要大于主堆石区。
|
图 2 有限元计算的水布垭面板坝最大断面竖向应变分布云图 Fig. 2 Contours of vertical strain at the maximum section in Shuibuya CFRD obtained by FEM simulations |
图 3是满蓄时最大断面应力水平分布云图,坝轴线上游侧应力水平普遍低于0.3,这是因为蓄水时水压力从近似小主应力方向施加,因此,应力莫尔圆远离破坏线。坝轴线下游侧坝体内应力水平也比较低,下游坝坡局部范围内的最大应力水平仅0.48,可见,面板堆石坝内堆石体的应力水平很低,很难达到《土工试验规程》(SL 237—1999)建议的用以确定双曲线模型参数的应力水平范围。

|
图 3 有限元计算的水布垭面板坝最大断面应力水平分布云图 Fig. 3 Contours of stress level at the maximum section in Shuibuya CFRD obtained by FEM simulations |
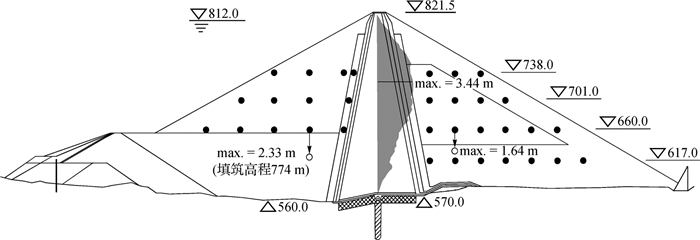
图 4给出了我国澜沧江糯扎渡心墙堆石坝(最大坝高261.5 m)最大断面的部分沉降监测结果,其中,砾石土心墙内的沉降分布如阴影部分所示。心墙内最大沉降约3.44 m,位于高程736.6 m处,该测值是2012年7月底大坝填筑至808.0 m高程(距坝顶仅差13.5 m;临时坝高248 m),水库蓄水至770.0 m(挡水水头210.0 m)时的监测结果[11]。可以估算,736.6 m以下砾石土心墙料的平均竖向应变为3.44 m/166 m≈2.1%。有文献对糯扎渡心墙坝防渗土料的变形和渗透特性进行了反馈分析[12],其中,652 m高程处心墙的沉降测值约1.9 m,因此,652 m高程以下心墙料的平均竖直向应变为1.9 m/82 m≈2.3%。
|
图 4 糯扎渡心墙坝最大断面部分沉降监测结果(单位:m) Fig. 4 Some selected settlement monitoring data at the maximum section in Nuozhadu ECRD(unit:m) |
谭志伟等[13]对施工期上、下游堆石体沉降进行了分析,大坝填筑至774.1 m高程时(临时坝高约214 m),上游侧堆石体内最大沉降2.33 m,下游侧堆石体内最大沉降1.64 m,均位于660 m监测高程(见图 4)。该高程以下堆石体厚度分别约为100 m(上游)和90 m(下游),因此,上游高程660 m以下堆石料的平均竖向应变为2.33 m/100 m≈2.3%;下游高程660 m以下堆石料的平均竖向应变为1.64 m/90 m≈1.8%。
图 5是采用三维有限元法模拟大坝填筑和蓄水过程得到的最大断面竖直向应变分布云图,其中计算模型采用邓肯E-B模型,参数由变形监测资料反演分析得到[12]。填筑完成时,该断面的最大竖直向应变约为5.6%,位于心墙底部。根据反演分析结果,坝壳堆石料的模量基数k(见式(1))约为砾石土心墙料模量基数的3倍[12],因此,可以明显地看出心墙内的竖直向应变大于两侧坝壳,即产生所谓的拱效应。

|
图 5 有限元计算的糯扎渡心墙坝最大断面竖直向应变分布云图 Fig. 5 Contours of vertical strain at the maximum section in Nuozhadu ECRD obtained by FEM simulations |
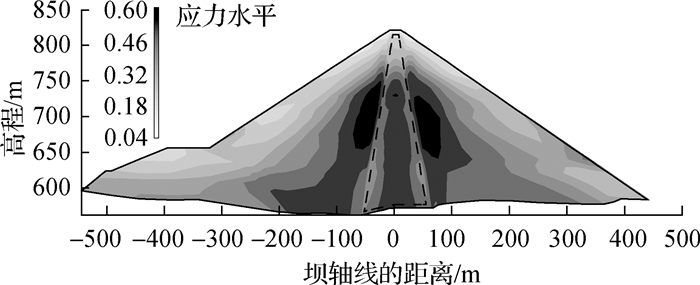
图 6是填筑竣工时最大断面堆石体和心墙料的应力水平分布云图,应力水平大体上以坝轴线为界,在两侧坝壳内呈对称分布。由于坝壳料与心墙料变形模量差异大,因此两者接触界面上相互滑移,产生剪切作用的趋势强烈,从而使该部位应力水平较高,最大值约0.6。两侧坝壳以及心墙内部绝大部分区域内应力水平不超过0.5,如图 6所示。Wu等基于反馈分析得到的坝料应力变形参数,分析了满蓄时坝体内应力水平分布情况[12]。对于下游侧堆石料,由于水压力作用大体上是从小主应力方向施加的,应力莫尔圆因蓄水而远离破坏线,故应力水平普遍低于0.4;对于上游侧堆石料,蓄水后有效应力降低,且心墙向下游位移,造成堆石体有效围压降低,故应力莫尔圆接近破坏线,应力水平显著提高,心墙料与堆石料接触界面的局部范围内应力水平达到0.9以上。由此可见,心墙堆石坝下游侧堆石料应力水平在施工和蓄水过程中始终保持较低水平;上游侧堆石料应力水平在施工过程中较低,但蓄水后显著提高,其变化范围明显比《土工试验规程》(SL 237—1999)建议的用以确定双曲线模型参数的应力水平范围要广。
|
图 6 有限元计算的糯扎渡心墙坝最大断面应力水平分布云图 Fig. 6 Contours of stress level at the maximum section in Nuozhadu ECRD obtained by FEM simulations |
上述两座高度250 m级高土石坝实测沉降与应力变形计算分析结果表明:
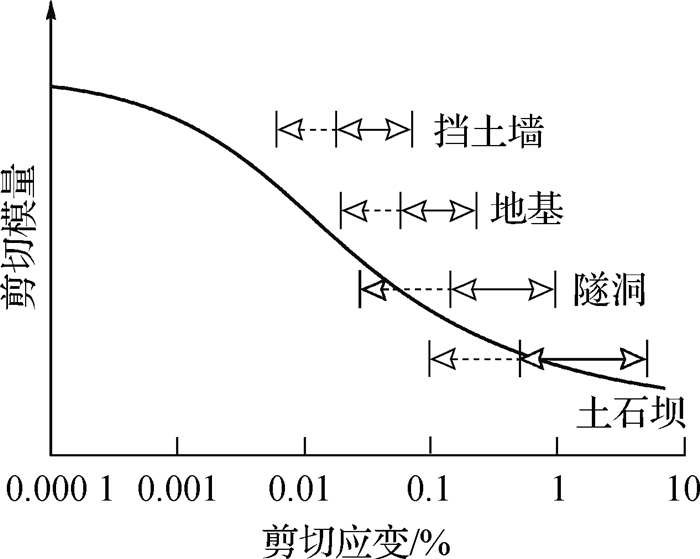
(1) 土石坝坝体内的最大竖直向应变可以达到5%左右,最大剪切应变应处于相同的量级。该应变量值要比挡土墙、地基、隧道等岩土工程常见应变范围大,如图 7所示。其中,挡土墙、地基和隧洞的剪应变范围取自文献[8],土石坝剪应变范围根据本文上述分析添加。对于最大竖向应变达到5%的土石坝工程而言,测试轴向应变小于0.1%时的变形模量意义不大,大型三轴剪切试验已经可以满足土石坝应力变形计算对应变范围与分辨率的要求。
|
图 7 典型岩土工程的剪切应变分布 Fig. 7 Strain ranges for typical geotechnical engineering |
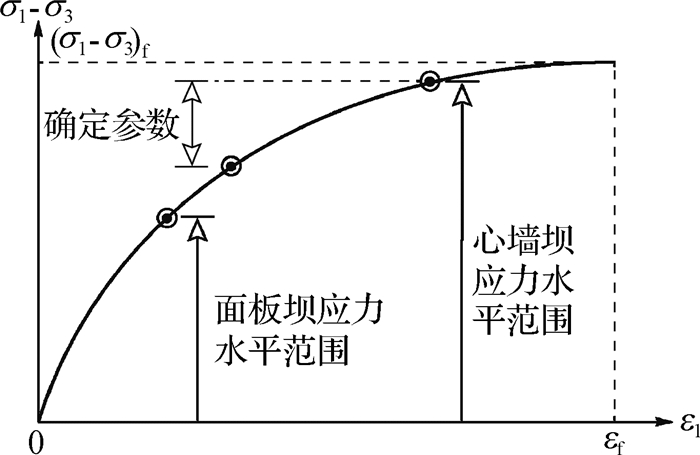
(2) 面板坝堆石料以及心墙坝下游侧堆石料填筑和蓄水后应力水平普遍较低;心墙坝上游侧堆石填筑过程中应力水平较低,但蓄水后可达到0.9以上,应力水平变化范围较大。采用双曲线模型模拟坝料轴向应力应变关系时,参数确定所用的应力应变段与坝体内实际应力应变范围明显不符,如图 8所示。土石坝应力变形计算中,绝大部分区域堆石料的应力应变关系实际上是通过少量试验结果外延得到的。
|
图 8 双曲线模型参数确定与土石坝实际应力状态的偏差 Fig. 8 Contradiction in parameter calibration and real states in earth and rockfill dams |
上述双曲线模型参数确定方法与土石坝实际应力状态之间的偏差增加了高土石坝变形计算结果的不确定性,其根本原因是双曲线模型难以全面模拟堆石料轴向应力应变关系,如低应力水平时应力应变试验结果在ε1-ε1/(σ1-σ3)平面上明显偏离线性假定[3]。因此,要解决上述问题,必须提出能够更好地模拟轴向应力应变关系的数学模型,更充分地运用低应力水平时的试验结果。
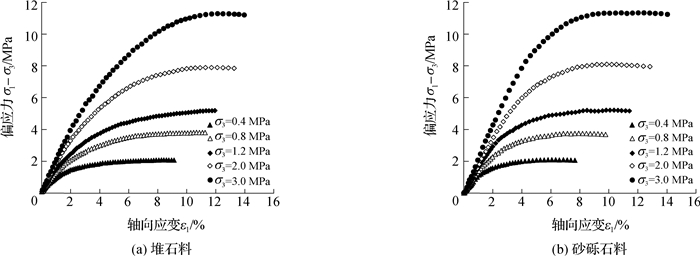
2 初始模量参数确定方法 2.1 应力应变数据的多项式拟合图 9中给出了我国新疆某面板砂砾石坝中筑坝堆石料与砂砾石料在5种不同围压下的三轴压缩试验结果,现以这两种粗颗粒坝料为例,说明本文拟建议的多项式拟合方法。
|
图 9 土石坝筑坝粗颗粒料的三轴压缩试验结果 Fig. 9 Triaxial compression experiments on typical coarse granular materials in rockfill dams |
记应力应变曲线上偏应力的峰值为(σ1-σ3)f,对应的轴向应变为εf(见图 8),则图 9中各围压下的试验结果可以用单位化的应变ε1/εf和单位化的偏应力(σ1-σ3)/(σ1-σ3)f表示。
现假定两者之间可以用多项式拟合(以4次多项式为例):
| $ \left( {{\sigma _1} - {\sigma _3}} \right)/{\left( {{\sigma _1} - {\sigma _3}} \right)_{\rm{f}}} = {c_4}{\left( {{\varepsilon _1}/{\varepsilon _{\rm{f}}}} \right)^4} + {c_3}{\left( {{\varepsilon _1}/{\varepsilon _{\rm{f}}}} \right)^3} + {c_2}{\left( {{\varepsilon _1}/{\varepsilon _{\rm{f}}}} \right)^2} + {c_1}\left( {{\varepsilon _1}/{\varepsilon _{\rm{f}}}} \right) $ | (4) |
则拟合试验数据的本质是确定c1~c4,使试验结果与式(4)预测结果误差最小。注意:式(4)满足ε1/εf=0时(σ1-σ3)/(σ1-σ3)f =0的基本条件。在应力应变曲线的峰值点处ε1/εf=1且(σ1-σ3)/(σ1-σ3)f =1,因此c1~c4还需满足∑ci=1的条件,故式(4)可以改写为
| $ y = {c_4}{x^4} + {c_3}{x^3} + {c_2}{x^2} + \left( {1 - {c_2} - {c_3} - {c_4}} \right)x $ | (5) |
或
| $ y - x = {c_4}\left( {{x^4} - x} \right) + {c_3}\left( {{x^3} - x} \right) + {c_2}\left( {{x^2} - x} \right) $ | (6) |
式中:x=ε1/εf;y=(σ1-σ3)/(σ1-σ3)f。
设有一组三轴压缩试验数据(xi, yi)(i=1~n),并引入下述向量b、向量c和矩阵A
| $ \mathit{\boldsymbol{b}} = {\left( {{y_1} - {x_1}\;\;{y_2} - {x_2} \cdots {y_n} - {x_n}} \right)^{\rm{T}}};\;\;\;\mathit{\boldsymbol{c = }}{\left( {{c_4}\;\;{c_3}\;\;{c_2}} \right)^{\rm{T}}} $ | (7) |
| $ \mathit{\boldsymbol{A = }}\left[ {\begin{array}{*{20}{c}} {{x_1}^4 - {x_1}}&{{x_1}^3 - {x_1}}&{{x_1}^2 - {x_1}}\\ {{x_2}^4 - {x_2}}&{{x_2}^3 - {x_2}}&{{x_2}^2 - {x_2}}\\ \vdots & \vdots & \vdots \\ {{x_n}^4 - {x_n}}&{{x_n}^3 - {x_n}}&{{x_n}^2 - {x_n}} \end{array}} \right] $ | (8) |
则运用式(6)拟合试验结果时的误差f可表示为
| $ f = {\left( {\mathit{\boldsymbol{b}} - \mathit{\boldsymbol{Ac}}} \right)^{\rm{T}}}\left( {\mathit{\boldsymbol{b}} - \mathit{\boldsymbol{Ac}}} \right) $ | (9) |
欲使误差最小化,只需令上式对各拟合参数ci的偏导数为零,即
| $ \frac{{\partial f}}{{\partial \mathit{\boldsymbol{c}}}} = 2{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{Ac }}-2{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{b = }}{\bf{0}} $ | (10) |
因此,只需求解式(10)中所给出的线性方程组即可确定c2~c4,并进一步确定c1,该过程本质是基于最小二乘法的参数拟合。
待各拟合参数确定后,由式(4)可以得到不同应变时的切线模量,即
| $ {E_{\rm{t}}} = \frac{{\partial \left( {{\sigma _1} - {\sigma _3}} \right)}}{{\partial {\varepsilon _1}}} = \frac{{{{\left( {{\sigma _1} - {\sigma _3}} \right)}_{\rm{f}}}}}{{{\varepsilon _{\rm{f}}}}}\left[ {4{c_4}{{\left( {\frac{{{\varepsilon _1}}}{{{\varepsilon _{\rm{f}}}}}} \right)}^3} + 3{c_3}{{\left( {\frac{{{\varepsilon _1}}}{{{\varepsilon _{\rm{f}}}}}} \right)}^2} + 2{c_2}{{\left( {\frac{{{\varepsilon _1}}}{{{\varepsilon _{\rm{f}}}}}} \right)}^1} + {c_1}} \right] $ | (11) |
因此,初始切线模量为
| $ {E_{\rm{i}}} = {c_1}{\left( {{\sigma _1} - {\sigma _3}} \right)_{\rm{f}}}/{\varepsilon _{\rm{f}}} $ | (12) |
式(11)和式(12)有两个优点:首先,多项式可以适应不同应力应变曲线形态,拟合参数c1~c4的确定可以使用从等向压缩应力状态到峰值应力状态之间整个加载过程的试验数据;其次,主要变量(σ1-σ3)f和εf可直接从试验结果读取,两者是大扰动状态时的物理量,受初始加载段端部嵌入误差的影响可以忽略。
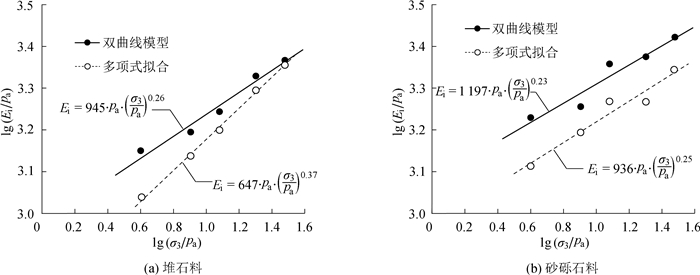
表 1列出了根据试验结果确定的不同围压下的拟合参数,式(12)确定的各围压下的初始切线模量以及根据指数函数式(1)拟合的参数k和n如图 10所示。根据双曲线模型参数确定方法得到的初始模量及其参数亦绘于图中,以便比较。从图 10中可以明显地看出,在试验所取的围压范围内,运用多项式拟合得到的两种粗颗粒料的初始切线模量要明显低于运用双曲线模型得到的初始切线模量。由于多项式拟合运用了整个加载过程的应力应变数据,因此可以认为其初始切线模量与实际情况更为符合,这意味着双曲线模型及其参数确定方法易高估粗颗粒料的初始模量。
| 表 1 基于两种坝料三轴压缩试验结果得到的拟合参数 Tab. 1 Fitting parameters obtained based on triaxial compression experiments on two dam materials |
|
图 10 两种模型得到的初始模量与围压的关系 Fig. 10 Relationships between initial modulus and confining pressure in two models |
粗颗粒料大型三轴压缩试验中,轴向加载初期的端部嵌入误差很难避免,因此在整理切线模量或应力剪胀关系等数据时初始段往往较为离散[14-15],可靠的参数确定方法应基本不受初始加载段数据的影响。
表 2列出了运用不同应力水平范围试验结果确定的c1值,其中标号①数据取自表 1,使用整个加载阶段的试验数据;标号②应力水平低于0.1时的试验数据弃用,从而消除初始加载段的影响。从表 2可以看出,两种方案确定的参数c1值相对误差基本不超过1%,这是因为在运用整个加载段试验数据,使式(9)中拟合误差最小化时,初始段所占比重和贡献较小,因此对参数拟合的影响不大。式(12)表明,初始模量与c1值成正比,因此是否运用应力水平低于0.1时的试验数据对初始模量的影响亦不会超过1%。可见,运用本文建议的多项式拟合方法时,即使初始加载段试验数据的可靠性较差,其对初始模量参数的影响几乎是可以忽略的,这一点与双曲线模型截然不同。双曲线模型中,初始加载段数据在ε1-ε1/(σ1-σ3)平面上明显不符合线性假定,是否包含该段试验数据对最佳拟合直线的方程式(含截距与斜率)影响很大,从而对初始模量参数造成很大影响。
| 表 2 运用不同应力水平段试验结果得到的拟合参数c1 Tab. 2 Obtained values of c1 based on different segments of triaxial compression experiments |
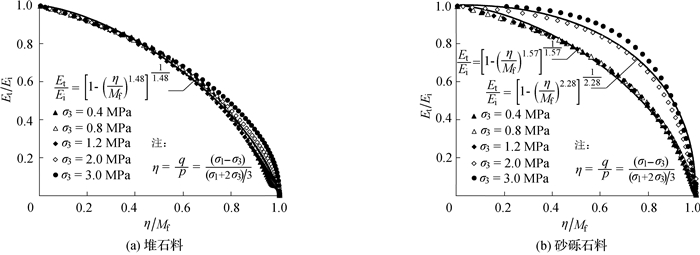
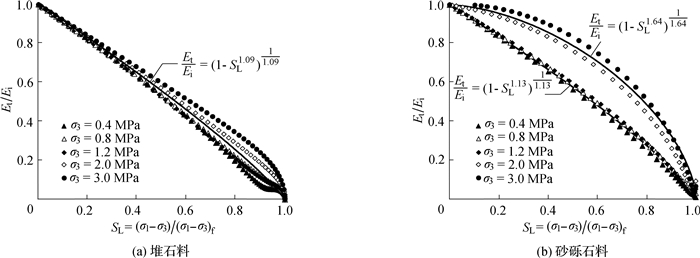
粗颗粒料的切线模量随着剪应力或者剪应变的增加而减小,原则上构建切线模量模型即可以采用剪应力,也可以采用剪应变作为自变量。式(1)所示的切线模量方程中采用了剪应力作为自变量(蕴含在应力水平SL中);堆石料动剪切模量模型中则普遍采用动剪应变作为自变量[2]。基于应力状态构建切线模量模型的一个突出优点是可以在其中蕴含破坏准则,如Rf=1时,式(1)所预测的切线模量在应力水平趋于1时趋向于0,即荷载不变时,应变可以无限发展。因此,SL =1就是破坏条件。在实际运用双曲线模型时,Rf < 1,即使SL =1,切线模量依然为正,故式(1)所示的切线模量方程无法模拟剪切破坏[16]。图 11和图 12中分别绘制了由式(11)计算的单位化切线模量(Et/Ei)与应力水平SL以及单位化应力比(η/Mf)之间的关系,其中应力比η是广义剪应力与平均有效应力之比;Mf是峰值应力比,可直接由试验结果确定[16]。
|
图 11 两种筑坝粗颗粒料切线模量与应力水平的关系 Fig. 11 Relationships between tangential modulus and stress level for two dam materials |
|
图 12 两种筑坝粗颗粒料切线模量与应力比的关系 Fig. 12 Relationships between tangential modulus and stress ratio for two dam materials |
从图 11(a)和图 12(a)中可以看出,堆石料在5种不同围压下,切线模量与应力水平或者应力比存在良好的归一化关系,尤其是应力水平SL低于0.6或者应力比η/Mf低于0.8时。对于砂砾石料,围压为0.4,0.8和1.2 MPa时,切线模量与应力水平或者应力比存在良好的归一化关系;但围压为2.0和3.0 MPa时,数据点明显偏离该归一化关系,如图 11(b)和图 12(b)所示。其原因是高围压下试验数据的整体趋势与低围压下不同(见图 9(b)),因此参数拟合时c3和c4的符号与低围压时相反(见表 1)。尽管不同围压下,图 11和图 12中数据点存在离散性,但所表现出的形态始终是一致的。通过尝试多种不同形式的函数,作者发现下述非线性函数可以较好地模拟切线模量与应力水平或者应力比之间的关系,即
| $ {E_{\rm{t}}} = {\left[ {1 - {{\left( {{S_{\rm{L}}}} \right)}^\alpha }} \right]^{\frac{1}{\alpha }}} \cdot {E_{\rm{i}}} = {\left[ {1 - {{\left( {{S_{\rm{L}}}} \right)}^\alpha }} \right]^{\frac{1}{\alpha }}} \cdot k \cdot {p_{\rm{a}}} \cdot {\left( {{\sigma _3}/{p_{\rm{a}}}} \right)^n} $ | (13) |
或者
| $ {E_{\rm{t}}} = {\left[ {1 - {{\left( {\eta /{M_{\rm{f}}}} \right)}^\beta }} \right]^{\frac{1}{\beta }}} \cdot {E_{\rm{i}}} = {\left[ {1 - {{\left( {\eta /{M_{\rm{f}}}} \right)}^\beta }} \right]^{\frac{1}{\beta }}} \cdot k \cdot {p_{\rm{a}}} \cdot {\left( {{\sigma _3}/{p_{\rm{a}}}} \right)^n} $ | (14) |
式中:α和β分别是采用应力水平和应力比作为应力变量时的拟合参数。注意:因多项式拟合得到的Ei与围压σ3在双对数图中亦大体呈线性关系,故式(13)和(14)中仍然采用了指数型初始模量表达式。图 11和图 12中运用数据点确定了两种粗粒料的参数α和β,并将模拟曲线与数据点进行了对比,其中堆石料直接运用5种围压下的所有数据确定参数;砂砾石料分别运用围压为0.4,0.8和1.2 MPa以及围压为2.0和3.0 MPa时的两组数据确定了两组参数。
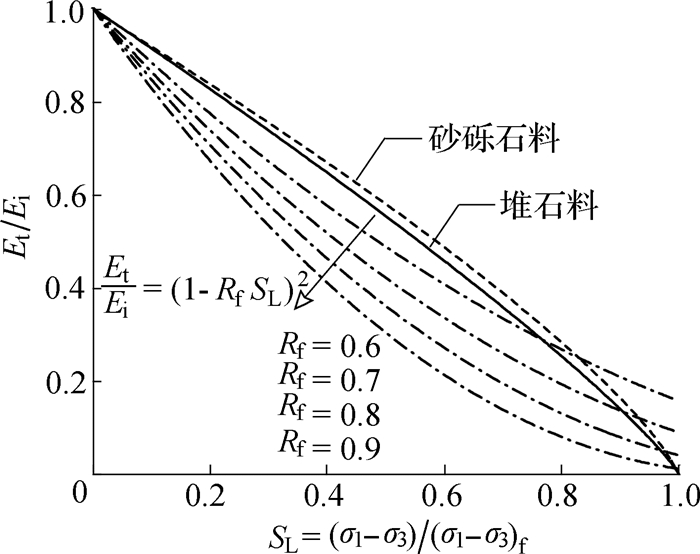
图 13中对比了式(1)和式(13)模拟曲线的差异,其中实线和虚线是根据式(13)及图 11和图 12中参数确定的曲线,是三轴压缩试验结果的最佳拟合;点划线是不同破坏比Rf时,由式(1)预测的曲线。可以看出,对于粗颗粒料常见的破坏比范围以及土石坝坝体内粗颗粒料应力水平范围,双曲线模型预测的不同应力水平时的单位化切线模量(Et/Ei)要低于实际值;而当应力水平接近于1时,双曲线模型会高估粗粒料的实际切线模量。双曲线模型在剪切应力状态下对于单位化切线模量的低估效应和等向压缩应力状态下对于初始切线模量的高估效应可以相互抵消,对土石坝应力变形计算结果的最终影响取决于何种效应更为显著。
|
图 13 两种模量衰减函数的差异 Fig. 13 Differences in modulus degradation functions |
我国土石坝应力变形计算普遍采用双曲线函数模拟轴向应力应变关系,其参数大多通过常规三轴压缩试验确定。本文基于高土石坝实测变形资料、筑坝粗颗粒材料三轴压缩试验以及土石坝三维有限元计算结果对上述模型和参数确定方法的合理性进行了分析;建议了轴向应力应变数据的多项式拟合方法和切线模量表达式,得出的主要结论如下:
(1) 高度250 m级的高混凝土面板堆石坝和心墙堆石坝最大竖向应变可以达到5%左右,该应变量值比挡土墙、地基、隧道等岩土工程常见应变范围大,测试轴向应变小于0.1%时的变形模量对于静力加载问题的意义不大,现行大型三轴剪切试验已经可以满足高土石坝应力变形计算对应变范围的要求。
(2) 土石坝坝体内应力水平普遍较低,采用双曲线模型模拟坝料轴向应力应变关系时,大多采用高应力水平段的试验数据确定参数,参数确定和实际应力水平范围的不协调增加了现行土石坝应力变形计算结果的不确定性。
(3) 应力应变数据的多项式拟合方法可以充分利用整个加载过程中的试验数据,受到初始加载阶段试验结果的影响较小,且可以避免直接处理试验数据时的振荡现象,可使参数确定时的不确定性大为降低。
(4) 双曲线模型有高估等向压缩应力状态下初始切线模量,低估剪切应力状态下单位化切线模量的两种相反趋势,运用于土石坝应力变形计算时,两种效应可能相互抵消,最终计算结果与实测结果的差异取决于何种效应更为显著。
本文对堆石料和砂砾石料进行数据处理时采用了4次多项式拟合试验结果,并根据拟合参数确定初始模量参数,研究剪切模量随应力水平和应力比的变化规律,实际运用时可以根据需要选择合适的项次。
| [1] |
DUNCAN J M, CHANG C Y. Nonlinear analysis of stress and strain in soils[J]. Journal of Soil Mechanics and Foundations Division, 1970, 96(SM5): 1629-1653. |
| [2] |
沈珠江. 理论土力学[M]. 北京: 中国水利水电出版社, 2000. ( SHEN Zhujiang. Theoretical soil mechanics[M]. Beijing: China Water and Power Press, 2000. (in Chinese))
|
| [3] |
刘大康, 刘京茂, 孔宪京, 等. 筑坝堆石料邓肯—张模型参数确定方法的改进[J]. 水利与建筑工程学报, 2016, 14(3): 91-95. ( LIU Dakang, LIU Jingmao, KONG Xianjing, et al. An improved method to determine Duncan-Chang model parameters of rockfill material[J]. Journal of Water Resources and Architectural Engineering, 2016, 14(3): 91-95. DOI:10.3969/j.issn.1672-1144.2016.03.017 (in Chinese)) |
| [4] |
KUMAR J, CLAYTON C R I. Effect of sample torsional stiffness on resonant column test results[J]. Canadian Geotechnical Journal, 2007, 41(2): 221-230. |
| [5] |
LINGS M L, GREENING P D. A novel bender/extender element for soil testing[J]. Géotechnique, 2001, 51(8): 713-717. DOI:10.1680/geot.2001.51.8.713 |
| [6] |
CLAYTON C R I, THERON M, BEST A I. The measurement of vertical shear-wave velocity using side-mounted bender elements in the triaxial apparatus[J]. Géotechnique, 2004, 54(7): 495-498. DOI:10.1680/geot.2004.54.7.495 |
| [7] |
SCHOLEY G K, FROST J D, PRESTI D C F, et al. A review of instrumentation for measuring small strains during triaxial testing of soil specimens[J]. Geotechnical Testing Journal, 1995, 18(2): 137-156. DOI:10.1520/GTJ10318J |
| [8] |
CLAYTON C R I. Stiffness at small strain: research and practice[J]. Géotechnique, 2011, 61(1): 5-37. DOI:10.1680/geot.2011.61.1.5 |
| [9] |
ENOMOTO T, QURESHI O H, SATO T, et al. Strength and deformation characteristics and small strain properties of undisturbed gravelly soils[J]. Soils and Foundations, 2013, 53(6): 951-965. DOI:10.1016/j.sandf.2013.10.004 |
| [10] |
杨启贵, 刘宁, 孙役, 等. 水布垭面板堆石坝筑坝技术[M]. 北京: 中国水利水电出版社, 2010. ( YANG Qigui, LIU Ning, SUN Yi, et al. Construction technologies in the Shuibuya concrete face rockfill dam[M]. Beijing: China Water and Power Press, 2010. (in Chinese))
|
| [11] |
张宗亮, 冯业林, 相彪, 等. 糯扎渡心墙堆石坝防渗土料的设计、研究与实践[J]. 岩土工程学报, 2013, 35(7): 1323-1327. ( ZHANG Zongliang, FENG Yelin, XIANG Biao, et al. Design, researches and practices of impervious materials for core wall of Nuozhadu hydropower station[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(7): 1323-1327. (in Chinese)) |
| [12] |
WU Y K, ZHANG B Y, YU Y Z, et al. Consolidation analysis of Nuozhadu high earth-rockfill dam based on the coupling of seepage and stress-deformation-physical state[J]. International Journal of Geomechanics, 2016, 16(3): 04015085. DOI:10.1061/(ASCE)GM.1943-5622.0000555 |
| [13] |
谭志伟, 邹青, 刘伟. 糯扎渡水电站高心墙堆石坝监测设计创新与实践[J]. 水力发电, 2012, 38(9): 90-99. ( TAN Zhiwei, ZOU Qing, LIU Wei. Innovation and practice on monitoring design of Nuozhadu high core rockfill dam[J]. Water Power, 2012, 38(9): 90-99. DOI:10.3969/j.issn.0559-9342.2012.09.026 (in Chinese)) |
| [14] |
BEEN K, JEFFERIES M. Stress-dilatancy in very loose sand[J]. Canadian Geotechnical Journal, 2004, 41(5): 972-989. DOI:10.1139/t04-038 |
| [15] |
PRADHAN T B S, TATSUOKA F, SATO Y. Experimental stress-dilatancy relations of sand subjected to cyclic loading[J]. Soils and Foundations, 1989, 29(1): 45-64. DOI:10.3208/sandf1972.29.45 |
| [16] |
王庭博, 陈生水, 傅中志. "南水"双屈服面模型的两点修正[J]. 同济大学学报(自然科学版), 2016, 44(3): 362-368. ( WANG Tingbo, CHEN Shengshui, FU Zhongzhi. Two modifications to Shen Zhujiang's double yield surfaces model[J]. Journal of Tongji University(Natural Science), 2016, 44(3): 362-368. (in Chinese)) |
2. Key Laboratory of Earth-Rock Dam Failure Mechanism and Safety Control Techniques, Ministry of Water Resources, Nanjing 210029, China;
3. Jiangning Water Resources Bureau of Nanjing, Nanjing 211112, China
 2019
2019 